Haryana Board Class 7 Maths Solutions For Chapter 9 Perimeter And Area

Haryana Board Class 7 Maths Solutions For Chapter 9 Perimeter And Area

Key Concepts

1. Perimeter: Perimeter is the distance around a closed figure.
2. Area: Area is the region occupied by a closed figure.
3. Remember:
   1. Perimeter of a regular polygon = number of sides x length of one side
   2. Perimeter of square = 4 x side
   3. Perimeter of a rectangle = 2x(l+b)
   4. Area of a rectangle = l x b
   5. Area of a square = side x side
   6. Increase of perimeter does not necessarily imply that area also increases.

• A quadrilateral is a closed figure with four sides, four angles and four vertices.
• Quadrilateral ABCD is said to be a convex quadrilateral if all line segments joining points in the interior of the quadrilateral also tie in interior of the quadrilateral.
• Quadrilateral PQRS is said to be a concave quadrilateral if all line segments joining points in the interior.of the quadrilateral do not
  necessarily lie in the interior of the quadrilateral.
• Trapezium is a quadrilateral with one pair of parallel sides.
• The diagonals ofa parallelogram bisect each other.
• The diagonals of a rhombus are perpendicular bisectors of one another.
• Area of parallelogram = base x height
  Area of rectangle = length x breadth (length = base; breadth = height)
• If all the sides of a parallelogram are equal,it is called a Rhombus’.
• The area of a rhombus is equal to half of the product of its diagonals i.e., A = \( \frac{1}{2} d1:d2 \)
• The approximate value of the ratio of the circumference to the diameter of a circle is \( \frac{22}{7} \) or 3.14. It is a constant and is denoted by π (Pi).
• \( \frac{c}{d} \) = where ‘c’ is the circumference of the circle and ‘d’ is its diameter

Since, \( \frac{c}{d} \) =
= n, where ‘c’ is the circumference of the circle and W is its diameter.
= n, c= nd

Since, diameter of a circle is twice the radius i.e. d = 2r, c=π x 2r or c=2πr.

The area of a triangle is equal to half of the product of its base (b) and height (h) i.e. A =\( \frac{1}{2} \) bh

Solutions To Try These

Find the area of the following parallelograms:

1)

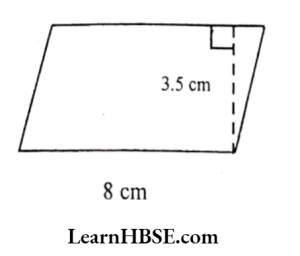
Solution:

Base = 8 cm

Height = 3.5 cm

Area of the parallelogram= base x height = 8 X 3.5 = 28 cm²

2)

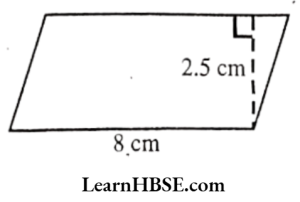
Solution:

Base = 8 cm

Height = 2.5 cm

Area of the parallelogram=base X height = 8 X 2.5 = 20 cm²

Haryana Board Class 7 Maths Perimeter and Area Solutions

3) In a parallelogram ABCD, AB = 7.2 cm, and the perpendicular from C on AB is 4.5 cm.

Solution:

Base = 7.2 cm

Height = 4.5 cm

Area of the parallelogram = base X height = 7,2 X 4.5 = 32. 40 cm²

Solutions To Try These

1. Try the above activity with different types of triangles.

Solution:

Try yourself

2. Take different parallelograms. Divide each of the parallelograms into two triangles by cutting along any of its diagonals. Are the triangles congruent?

Solution:

Try yourself.

Hint: All the congruent triangles are equal in area but the triangles equal in area need not be congruent.

Haryana Board Class 7 Maths Solutions For Chapter 9Exercise-9.1 :

1. Find the area of each of the following parallelogram:

1)

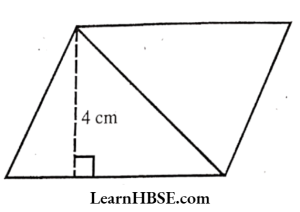
Solution:

Base = 7 cm 7cm

Height = 4 cm

Area of parallelogram= base X height

= 7 x 4 = 28 cm²

2)

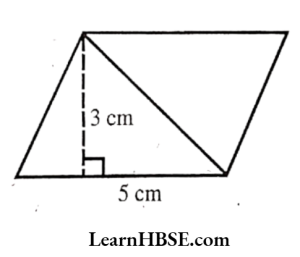
Solution:

Base = 5 cm

Height = 3 cm

Area of parallelogram = b x h

= 5×3 = 15 cm²

3)

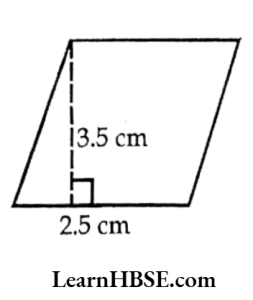
Solution:

Base = 2.5 cm

Height = 3.5 cm

Area of parallelogram =b x h

= 2.5 x 3.5 = 8.75 cm²

Area of parallelogram =b x h

= 2.5 x 3.5 = 8.75 cm²

Class 7 Maths Chapter 9 Perimeter and Area Haryana Board

4)

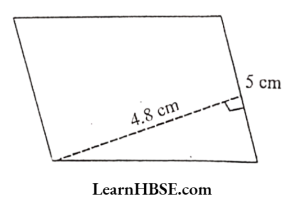
Solution:

Base = 5 cm

Height = 4.8 cm

Area of parallelogram = b x h

= 5 X 4.8 = 24 cm²

HBSE Class 7 Rational Numbers Solutions Ex 9.1

5)

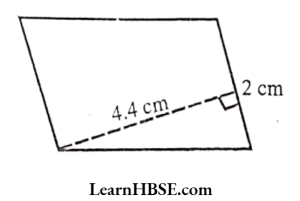
Solution:

Base = 2 cm

Height = 4.4 cm

Area of parallelogram = base x height

= 2×4.4 = 8.8 cm²

2. Find the area of each of the following triangles:

Solution:

1)

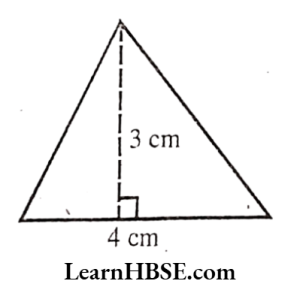
Base = 4 cm

Height = 3 cm

Area of triangle = \( \frac{1}{2} b x h \)x b x h

\( =\frac{1}{2} \times 4 \times 3=\frac{12}{2}=6 \mathrm{~cm}^2 \)

2)

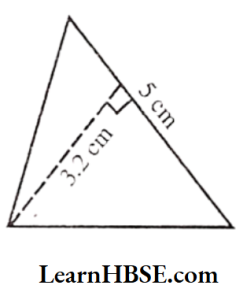
Base = 5 cm

Height= 3.2 cm

Area of triangle = \( \frac{1}{2} \times b \times h \)

\( =\frac{1}{2} \times 5 \times 3.2=\frac{16}{2}=8 \mathrm{~cm}^2 \)

3)

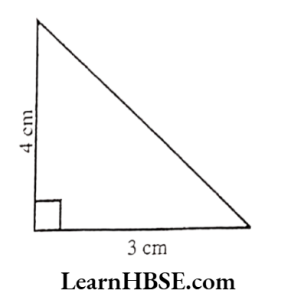
Solution:

Base = 3 cm

Height =4 cm

Area of triangle =\( \frac{1}{2} \times b \times h \)

\( =\frac{1}{2} \times 3 \times 4=\frac{12}{2}=6 \mathrm{~cm}^2 \)

HBSE Class 7 Rational Numbers Solutions Ex 9.2

4)

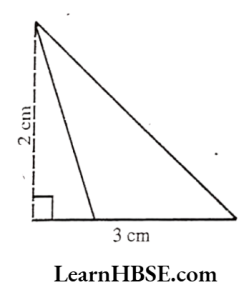
Solution:

Base = 3 cm

Height = 2 cm

Area of triangle = \( \frac{1}{2} \times b \times h \)

\( =\frac{1}{2} \times 3 \times 2=\frac{6}{2}=3 \mathrm{~cm}^2 \)

Haryana Board 7th Class Maths Perimeter and Area Questions and Answers

3. Find the missing values:

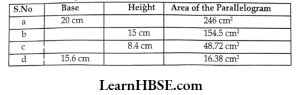
Solution:

Area of parallelogram = bh

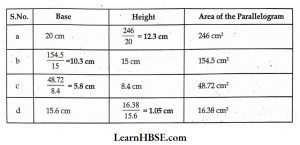
4. Find the missing values:

 

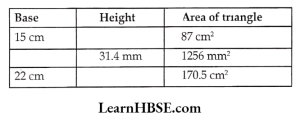
Solution:

Area of triangle = \( \frac{1}{2} \mathrm{bh} \)

5. PQRS is a parallelogram. QM is the height from Q to SR and QN is the height from Q to PS.If SR = 12 cm and QM = 7.6 cm.

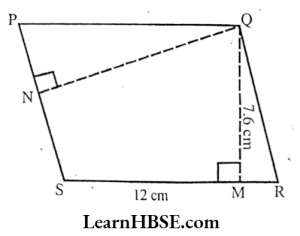
Find:

1) The area of the parallelogram PQRS

2) QN,if PS = 8 cm

Solution:

1)

PQRS is a parallelogram.

Its base SR = 12 cm

Height QM = 7.6 cm

Area of the parallelogram PQRS

= base x height

=12×7.6 = 91.2 cm2

2) Base PS = 8 cm

Corresponding height QN =?

Area of parallelogram PQRS

= 91.2 cm²

= 8 X QN = 91.2

QN = \( \frac{91.2}{8}=11.4 \mathrm{~cm} \)

Key Questions in Rational Numbers Ex 9.1 for Class 7 HBSE

6. DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD. If the area of the parallelogram is 1470cm², AB = 35cm, and AD = 49 cm, find the length of BM and DL.

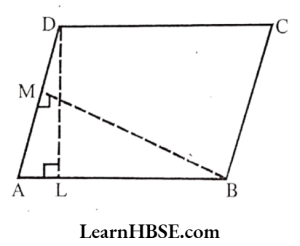
Solution:

ABCD is a parallelogram;

AD = 49 cm

Base AB = 35 cm

DL and BM are the heights.

Area of parallelogram ABCD =1470 cm²

AD X BM = 1470

49 X BM = 1470

\( \mathrm{BM}=\frac{1470}{49}=30 \mathrm{~cm} \)

The length of BM = 30 cm

Area of parallelogram ABCD = 1470 cm²

AB x DL = 1470

35 X DL = 1470

\( \mathrm{DL}=\frac{1470}{35}=42 \mathrm{~cm} \)

The length of DL 42 cm

Chapter 9 Perimeter and Area Class 7 Solutions in Hindi Haryana Board

7. AABC is right-angled at A. AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm, and AC = 12 cm. Find the Area of ΔABC. Also, find the length of AD.

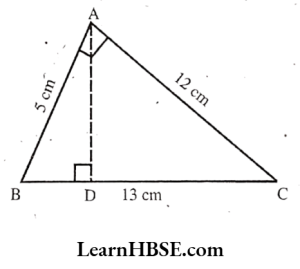
Solution:

AABC is right-angled at A.

When we take base AC = 12 cm and height AB = 5 cm

Area of the triangle ABC

\( \begin{aligned}
& =\frac{1}{2} \times \text { base } \times \text { height } \\
& =\frac{1}{2} \times 12 \times 5=30 \mathrm{~cm}^2
\end{aligned} \)

AD is perpendicular to BC.

When we take base BC = 13 cm

Area of the triangle ABC = 30 cm2

Its height AD =?

\( \begin{aligned}
& \frac{1}{2} \times \text { base } \times \text { height }=30 \\
& \frac{1}{2} \times 13 \times \mathrm{AD}=30
\end{aligned} \) \( \mathrm{AD}=\frac{30 \times 2}{13}=\frac{60}{13} \mathrm{~cm}=4 \frac{8}{13} \mathrm{~cm}\)

8. ΔABCis isosceles with AB=AC=7.5 cm and BC = 9 cm. The height AD from A to BC, is 6 cm. Find the area of AABC. What will be height from C to AB i.e CE?

Solution:

AABC is an isosceles triangle.

AB = AC = 7.5.cm

Base BC = 9 cm

Height AD = 6 cm

Area of triangle ABC

\( \begin{aligned}
& =\frac{1}{2} \times \text { base } \times \text { height } \\
& =\frac{1}{2} \times 9 \times 6=\frac{54}{2}=27 \mathrm{~cm}^2
\end{aligned} \)

Area of the AABC = 27 cm²

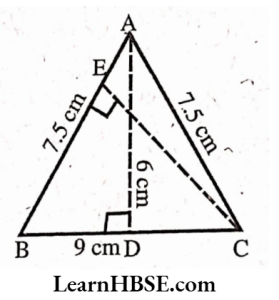
When we take base AB = 7.5 cm

Its corresponding height CE =?

Area of triangle ΔABC

\( \begin{aligned}
& =\frac{1}{2} \times \text { base } \times \text { height } \\
& =\frac{1}{2} \times 7.5 \times \mathrm{CE}=27 \\
& C E=\frac{27 \times 2}{7.5}=\frac{54}{7.5}=7.2 \mathrm{~cm}
\end{aligned} \)

The height from C to AB is 7.2 cm

Practice Problems Rational Numbers HBSE Class 7

Solutions To Try These

From the figure,

Which square has the larger perimeter?

Solution: The outer square has the larger perimeter.

Which is larger, perimeter of smaller square or the circumference of the circle?

Solution:

The circumference of the circleis larger.

Solutions To Try These

Draw circles of different radii on a graph paper. Find the area by counting the number of squares. Also find the area by using formula. Compare the two answers.

Solution:

Try yourself with the help your teacher.

Haryana Board Class 7 Maths Solutions For Chapter 9 Exercise-9.2

1. Find the circumference of the circles with the following radius:

1) 14 cm

Solution:

Radius of the circle (r) = 14 cm

Circumference of the circle = 2Πr

\( =2 \times \frac{22}{7} \times 14 \)

= 88 cm

2) 28 mm

Solution:

Radius of the circle (r) = 28 mm

Circumference of the circle = 2Πr

\( =2 \times \frac{22}{7} \times 28 \)

Haryana Board Class 7 Maths Exercise 9.1 Solutions

3) 21 cm

Solution:

Radius of the circle (r) = 21 cm

Circumference of the circle = 2Πr

=176 mm

\( =2 \times \frac{22}{7} \times 21 \)

= 132 cm

2. Find the area of the following circles, given that :

1) radius = 14 mm

Solution:

Radius of the circle (r) = 14 mm

Area of the circle = Πr²

\( =\frac{22}{7} \times 14 \times 14=616 \mathrm{~mm}^2\)

2)diameter = 49 m

Solution:

Diameter = 49 m

Radius = \( \frac{49}{2} \mathrm{~m} \) \( r=\frac{d}{2} \)

Area of the circle = Πr²

\( \begin{aligned}
& =\frac{22}{7} \times \frac{49}{2} \times \frac{49}{2} \\
& =11 \times 7 \times \frac{49}{2}
\end{aligned} \) \( =\frac{3773}{2} \)

= 1886.5 m2

3) radius = 5 cm

Solution:

Radius ( r) 5 cm

Area of the circle = Πr²

\( =\frac{22}{7} \times 5 \times 5=\frac{550}{7} \mathrm{~cm}^2=78.5 \mathrm{~cm}^2 \)

3. if the circumference of a circular sheet is 154 m, find its radius. Also, find the area of the sheet.

Solution:

Circumference of the circular sheet 154 m

2Πr =154

\( 2 \times \frac{22}{7} \times r=154 \) \( \begin{aligned}
r=154 \times \frac{1}{2} \times \frac{7}{22} & \\
& =\frac{7 \times 7}{2} \\
& =\frac{49}{2}
\end{aligned} \)

Area of the circular sheet = Πr²

\( \begin{aligned}
& =\frac{22}{7} \times \frac{49}{2} \times \frac{49}{2} \\
& =\frac{11 \times 7 \times 49}{2}=\frac{3773}{2}=1886.5 \mathrm{~m}^2
\end{aligned} \)

4. A gardener wants to fence a circular garden of diameter 21m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the cost of the rope, if it costs Rs. 4 per meter. \( \text { (Take } \pi=\frac{22}{7} \text { ) } \)

Solution:

Diameter of the circular garden = 21 m

Circumference of the garden = Πd

\( =\frac{22}{7} \times 21=66 \mathrm{~m}\)

Length of the rope to make one round of fence = 66 m

Length of the rope to make 2 rounds of fence = 66 x 2 = 132 m

Cost of 1 m rope = Rs. 4

Cost of 132 m rope = Rs, 4 x 132= Rs. 528

HBSE 7th Class Rational Number Word Problems

5. From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet (Take π = 3.14)

Solution:

Radius of a circular sheet = 4 cm

Area of the outer circle = Πr³

=> 3.14 x 4 x 4 = 3.14 X 16 = 50.24 cm³

Radius of the inner circle =3 cm

Area of the inner circle = Πr²

= 3.14 x 3 x 3 = 28.26 cm³

Area of the remaining sheet

= Area of outer circle – Area of inner circle

= 50.24 – 28.26 = 21.98 cm²

Important Questions for Class 7 Maths Chapter 9 Haryana Board

6. Saima wants to put a lace on the edge of a circular tabic cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs Rs. 15. (Take π = 3.14)

Solution:

Diameter of the circular table cover = 1.5 m

Circumference of the table cover =πd

=3.14 x 1.5 = 4.71 m

Length of the lace required

Circumference of the circular table cover = 4.71 m

Cost of lm of lace = Rs. 15

Cost of 4.71 m of lace = Rs. 15 x 4.71 = Rs. 70.65

7. Find the perimeter of the adjoining figure, which is a semicircle including its diameter.

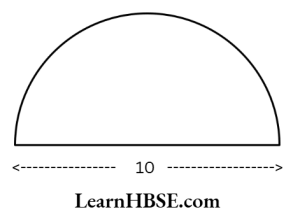
Solution:

Diameter of the semicircle ‘d’= 10 cm

Circumference of the semicircle

\( \begin{aligned}
& =\frac{1}{2} \text { (circumference of the circle) } \\
& =\frac{1}{2} \pi \mathrm{~d} \\
& =\frac{1}{2} \times 3.14 \times 10=3.14 \times 5=15.7 \mathrm{~cm}
\end{aligned} \)

Perimeter of semicircle

=Circumference of semicircle + diameter

= 15.7 + 10 = 25.7 cm

8. Find the cost of polishing a circular table – top of diameter 1.6 m, if the rate of polishing is Rs. 15/mJ. (Take Π = 3.14)

Solution:

Diameter of the circular table-top = 1.6m

Radius = \( \frac{1.6}{2} \) = 0.8m

Area of the table-top

= Πr²

= 3.14 x (0.8)²

= 3.14 x 0.8 x 0.8

= 3.14 x 0.64 = 20096 m²

Cost of l m² area = Rs. 15

Cost of 2.0096 m²area = Rs 15 x 2.0096

= Rs 30 .144

= Rs 30. 14 (approx)

9. Shazli took a wire of length 44 cm and bentit into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides ? Which figure encloses more area, the circle or the square? \( \text { (Take } \pi=\frac{22}{7} \text { ) } \)

Solution:

Length of the wire = 44 cm

Itis bent into the shape of a circle.

Circumference of the circle = 44 cm

27 πr = 44

\( 2 \times \frac{22}{7} \times r=44 \) \( \mathrm{r}=44 \times \frac{1}{2} \times \frac{7}{22}=7 \mathrm{~cm} \)

Radius of that circle = 7 cm

Area of the circle = Πr²

\( =\frac{22}{7} \times\left(7^2\right)=\frac{22}{7} \times 7 \times 7=154 \mathrm{~cm}^2 \)

The wire is bent into the shape of a square.

Perimeter of the square = Length of the wire 4 X side = 44

Side =\( \frac{44}{4} \) =11 cm

Area of the square = side x side = 11 X 11 = 121 cm²

The circle encloses more area than the square.

Important Concepts Rational Numbers Class 7 HBSE Chapter 9

10. From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm, and a rectangle of length 3 cm and breadth 1 cm are removed (as shown in the adjoining figure), find the area of the 22 remaining sheet.

Solution:

Radius of the circular card sheet=14 cm

Area of the circular card sheet

=πr²

\( =\frac{22}{7}(14)^2=\frac{22}{7} \times 14 \times 14 \)

=22 x 2 x 14 =616 cm²

Area of two circles of radius = 3.5 cms.

\( \begin{aligned}
& =2\left[\pi \mathrm{r}^2\right]=2\left[\frac{22}{7} \times(3.5)^2\right] \\
& =2\left[\frac{2 \dot{2}}{7} \times 3.5 \times 3.5\right]
\end{aligned} \)

= 2 X 38.5 = 77 cm²

Length of the rectangle = 3 cm

Breadth =1 cm

Area of this rectangle = l x b

=3 x 1=3 cm²

Area of the sheet = Area of the circular card sheet- Area of the two circles Area of the rectangle.

= 616-77-3

= 616-80

= 536 cm²

Step-by-Step Solutions for Perimeter and Area Class 7 Haryana Board

11. A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the leftover aluminium sheet? (Take π= 3.14)

Solution: Side of the square piece of an aluminium sheet = 6 cm

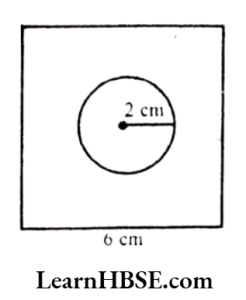
Area of this sheet = side x side = 6 x 6 = 36 cm²

Radius of the circle = 2 cm

Area of the circle

= Πr²

= 3.14 x(2)² = 3.14x2x2

= 3.14×4 = 12.56 cm²

Area of the aluminium sheet left over

= Area of the square- Area of the circle

= 36 -12.56 = 23.44 cm²

12. The circumference of a circleis 31.4 cm. Find the radius and area of the circle? (Take Π = 3.14)

Solution:

Circumference of a circle = 31.4 cm

2Πr= 31.4

2 X3.14 x r = 31.4

\( \mathrm{r}=\frac{31.4}{2 \times 3.14}=5 \mathrm{~cm} \)

Area of the circle = Πr²

= 3.14 X (5)²

= 3.14x5x5

= 3.14 X 25 = 78.5 cm²

13. A circular flowerbed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (Take π= 3.14)

Solution:

Diameter of the flower bed = 66 m

Radius of the flower bed = \( \frac{66}{2}=33 \mathrm{~m} \)

Area of the flower bed

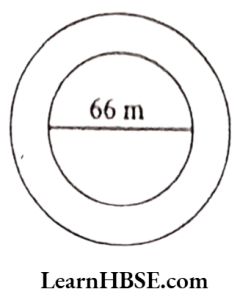
= πr²

= 3.14 x (33)²

= 3.14 X 33 X 33

= 3.14 X 1089 = 3419.46 m²

Width of the path = 4 m

Radius of the flower bed with path = 33 + 4 = 37 m

Area of the flower bed with path

= Π²

= 3.14 x(37)²

= 3.14x37x37

= 3.14×1369 = 4298.66 m²

Area of the path = Area of flowerbed with path- Area of the flower bed = 4298.66- 3419. 46 = 879.20 m²

14. A circular flower garden has an area of 314 m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take Π – 3.14)

Solution:

Area of the circular flower garden = 314 m²

Πr²= 314

3.14 xr² = 314

\( \frac{314}{100} \times r^2=314 \) \( \begin{aligned}
& 3.14 \times r^2=314 \\
& \frac{314}{100} \times r^2=314 \\
& r^2=314 \times \frac{100}{314}
\end{aligned} \)

r² = 100

r = 100 = 10×10 = 10 m

Given that the sprinkler can cover the area that has a radius 12m.

12 m > 10 m

The sprinkler will water the entire garden.

HBSE Class 7 Maths Chapter 9 Guide Rational Numbers

5. Find the circumference of the inner and outer circles, shown in the adjoining figure. (Take π= 3.14)

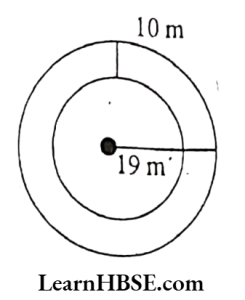
Solution:

Radius of the outer circle = 19m

Circumference of the outer circle

= 2Πr

= 2×3.14×19

= 38×3.14 = 119.32 m

Radius of the inner circle =19m-10m = 9m

Circumference of the inner circle

= 2Πr

= 2×3.14×9

= 18X3.14 = 56.52 m

16. How many times a wheel of radius 28 cm must rotate to go 352 m?

Solution:

Radius of the wheel = 28 cm

Circumference of the wheel = 27Πr

\( =2 \times \frac{22}{7} \times 28 \)

Distance covered by the wheel in one rotation = Circumference of the wheel 1 m = 100 cm

352 m = 352 x 100 = 35200 cm

= 2 X 22 x 4 = 176 cm

Number of times the wheel must rotate to go 352 m.

\( =\frac{35200}{176}=200 \text { times } \)

17. The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in1 horn? (Take Π = 3.14)

Solution:

Length of the minute hand of a circular clock =15 cm

Radius of the circular clock ‘r’=15 cm

Circumference of the circle = 27Πr

=2X3.14X15 = 94.2 cm

In one hour i.e., in 60 minutes; the minute hand of the clock completes 1 rotation.

The tip of the minute hand moves 94.2 cm in 1 hour.

Haryana Board Class 7 Maths Solutions For Chapter 9 Very Short Answer Questions

1. Define ‘Area’.

Solution:

The amount of surface enclosed by a closed figure is called its ‘area’.

2. Define ‘Perimeter’.

Solution:

Perimeter is the distance around a closed figure.

3. The area of a rectangular sheet is 500 cm². If the length of the sheet is 25 cm. What is its width?

Solution:

Length of the rectangular sheet (Z)=25 cm

Area of the rectangular sheet = 500 cm²

l x b = 500 => 25 x b = 500

\( b=\frac{500}{25}=20 \mathrm{~cm} \)

4. The perimeter of a rectangle is 180 cm. If the breadth of the rectangle is 40 cm. Find its length.

Solution:

The breadth of a rectangle = 40 cm

Perimeter of the rectangle = 180 cm

2 ( l + b ) = 180

2 ( l + 40) = 180

\( l+40=\frac{180}{2} \text { or } l+40=90 \)

l = 90 – 40 = 50 cm

5. Find the area of the parallelogram whose base is 10 cm and the height is 4 cm.

Solution:

Base of the parallelogram = 10 cm

Height = 4 cm

Area of the parallelogram = Base x Height = 10 X 4 = 40 cm²

Rational Numbers on the Number Line Class 7 Haryana Board

6. Find the area of the triangle whose base is 6 cm and height 3 cm:

Solution:

Area of triangle

\( \begin{aligned}
& =\frac{1}{2} \mathrm{bh} \\
& =\frac{1}{2} \times 6 \times 3=9 \mathrm{~cm}^2
\end{aligned} \)

7. What is the circumference of a circular 22 disc of radius 14 cm?\( \)

\( \text { (Take } \pi=\frac{22}{7} \text { ) } \)

Solution:

Radius of circular disc = 14 cm

Circumference of disc = 2Πr

\( =2 \times \frac{22}{7} \times 14=88 \mathrm{~cm} \)

8. Diameter of a circular garden is 9.8 m. Find its area.

Solution:

Diameter d = 9.8 m

Radius (r) = \(\frac{9.8}{2} \) = 4.9 m

Area of the cirle = Πr²

\( =\frac{22}{7} \times 4.9 \times 4.9=75.46 \mathrm{~m}^2 \)

9. Find the base of a triangle whose area is 220 cm2 and height is 11 cm.

Solution:

Given area of triangle = 220 cm²

\( \begin{aligned}
& \Rightarrow \frac{1}{2} \times \text { base } \times \text { height }=220 \mathrm{~cm}^2 \\
& \quad \text { (height }=11 \mathrm{~cm} \text { ) } \\
& \Rightarrow \frac{1}{2} \times \text { base } \times 11=220 \\
& \text { base }=\frac{220 \times 2}{11}=40 \mathrm{~cm}
\end{aligned} \)

10. Find the circumference of a circle whose radius is (1) 35 cm (2) 4.2 cm (3) 15.4 cm

Solution:

Circumference of a circle = 2Πr

1) r = 35 cm; circumference

= 2 x \( \frac{22}{7} \) x 35 cm = 220 cm

2) r = 4.2 cm; circumference

= 2 x \( \frac{22}{7} \) x 4.2 = 26.4 cm

3) r = 15.4 cm; circumference

= 2 x \( \frac{22}{7} \) x 15.4 = 26.4 cm

11. If the circumference of a circle is 264 cm, find its radius. \( \text { Take } \pi=\frac{22}{7} \) .

Solution:

Circumference of a circle = 2rcr = 264cm

Given

\( 2 \times \frac{22}{7} \times r=264 \)

r = \( \frac{264 x 7}{2 x 22} \) = 42 cm

12. If the circumference of a circle is 33 cm, find its diameter.

Solution:

Given

Circumference of a circle = Πd = 33 cm

i.e, \( \frac{22}{7} \times d=33 \)

d = \( \frac{33×7}{22} [latex] = [latex] \frac{21}{2} \) = 10.5 cm

Haryana Board Class 7 Maths Solutions For Chapter 9 Short Answer Questions

13. Find the area of each of the following triangles.

1)

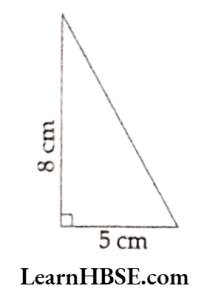
Solution:

1) Area of triangle = \( \frac{1}{2} \mathrm{bh} =

= [latex] \frac{1}{2} \) x 5 x 8 = 20 cm²

2)

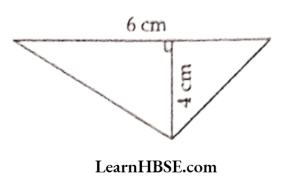
Solution:

2) Area of triangle = \( \frac{1}{2} \mathrm{bh}

= [latex] \frac{1}{2} \) x 6 x 4 = 12 cm²

3)

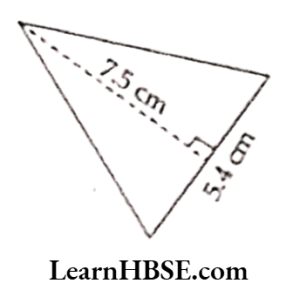
Solution:

3) Area of triangle = \( \frac{1}{2} \) x 5.4 x 7.5 = 20.25 cm²

4)

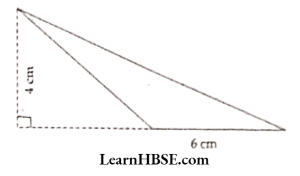
Solution:

4) Area of triangle = \( \frac{1}{2} \) x 6 x 4 = 12 cm²

14. ΔABC is right-angled at A. AD is perpendicular to BC AB = 5 cm, BC = 13 cm, and AC =12 cm. Find the area of ΔABC. Also, find the length of AD.

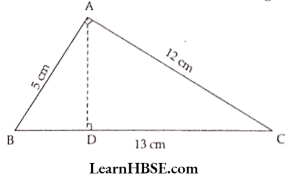
Solution:

ABC is a right-angled triangle, either AB or AC can be considered as base or height

Take AC (Base 12 cm); height (AB) = 5 cm

Area of triangle = \( \frac{1}{2} \mathrm{bh}=\frac{1}{2} \times 12 \times 5=30 \mathrm{~cm}^2 \) …….(1)

Now take BC (base) = 13 cm and AD =h

1/2 bh = area; substituting, 13 cm for base

\( \begin{aligned}
&\text { we get } \frac{1}{2} \times 13 \times \mathrm{h}=30 \mathrm{~cm}^2\\
&\text { height }=\frac{30 \times 2}{13}=\frac{60}{13}=4.6 \mathrm{~cm} \text { (nearly) }
\end{aligned} \)

15. APQRis isosceles withPQ = PR = 7.5 cm and QR = 9 cm. The height PS from P to QR is 6 cm. Find the area of ΔPQR. What will be the height from R to PQ i.e. RT?

Solution:

By Question, base QR = 9 cm; height PS = 6 cm

Area of triangle \( =\frac{1}{2} \mathrm{bh} \)

= \(\frac{1}{2}\)x9x6 = 27cm² (1)………

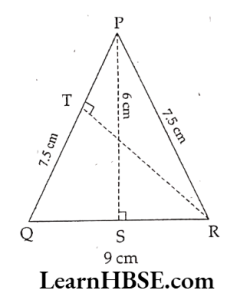
Again, take PQ as base = PR = 7.5 cm (It is a triangle) & Height (TR) =h cm

\( \begin{aligned}
& \frac{1}{2} \mathrm{bh}=\text { Area ; from } \\
& \frac{1}{2} \times 7.5 \times \mathrm{h}=27
\end{aligned} \)

Height = \( \frac{27×2}{75} \) x 10 (decimal removed)

\( =\frac{36}{5}=7.2 \mathrm{~cm} \)

16. Find the area of the following rhombuses.

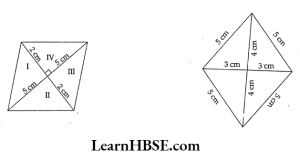
Solution:

Area of rhombus = \( \frac{1}{2} \mathrm{~d}_1 \mathrm{~d}_2 \)

\( \begin{aligned}
& =\frac{1}{2} \times 10 \times 4 \mathrm{~cm}^2 \\
& =20 \mathrm{~cm}^2
\end{aligned} \)

Solution:

Area of rhombus = \( \frac{1}{2} \mathrm{~d}_1 \mathrm{~d}_2 \)

\( =\frac{1}{2} \times 8 \times 6 \mathrm{~cm}^2 \)

= 24 cm²

Haryana Board Class 7 Maths Solutions For Chapter 9 Long Answer Questions

17. Find the circumference of circle whose diameter is

(1) 17.5 cm (2) 5.6 cm (3) 4.9 cm

Note: take \( \pi=\frac{22}{7}\) in the above two questions.

Solution:

Circumference of circle = Πd

1) Circumference of circle = \( \frac{22}{7} \times 17.5=55.0 \mathrm{~cm} \)

2) Circumference of circle =\( \frac{22}{7} \times 5.6=17.6 \mathrm{~cm} \)

3) Circumference of circle =\( \frac{22}{7} \times 4.9=15.4 \mathrm{~cm} \)

18. 1) Taking Π = 3.14, find the circumference of a circle whose radius is

(1) 8 cm (2) 15 cm (3) 20 cm

2) Calculate the radius of a circle whose circumference is 44 cm.

Solution:

1) Circumference of circle = 2Πr

1) given r = 8 cm and Π= 3.14, circumference = 2 x 3.14 x 8 = 50.24 cm

2) given r = 15 cm and Π = 3.14, circumference = 2 x 3.14 x 15 = 94.20 cm

3) given r=20 cm and Π= 3.14, circumference = 2 x 3.14 x 20 = 125.60 cm

2) Given circumference = 44 cm. To find radius, 27Πr = 44

i.e \( 2 \times \frac{22}{7} \times r=44 \)

r = \( \frac{44×7}{2×22} \)

= 7

Finding Rational Numbers Between Two Numbers Class 7 HBSE

19. Arectangle ABCD with AB = 8 cm, BC = 16 cm and AE = 4 cm.Find the area of ΔBCE. Is the area of ΔBEC equal to the sum of the area of ΔBAE and ΔCDE. Why?

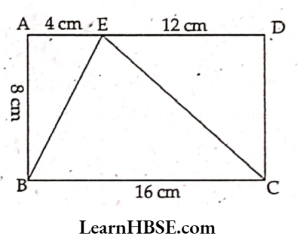
Solution:

Area of a rectangle =l xb = 16 x 8 cm² = 128 cm²

Area of a triangle (BEC) = \( \frac{1}{2} \mathrm{bh} \) = \( \frac{1}{2} \) x 16 x 8 = 64 cm²

Area of a triangle (BAE) =\( \frac{1}{2} \mathrm{bh} \) = \( \frac{1}{2} \) x 4 x 8 = 16 cm²

Area of a triangle (CDE) =\( \frac{1}{2} \mathrm{bh} \) = \( \frac{1}{2} \) x 8 x 12 = 48 cm²

Observation:

1) Area of triangle BEC = \( \frac{1}{2} \) (area of rectangle)

2)Area of A BAE +A CDE = Area of A BEC because area of A BEC = Area of A BEC = \( \frac{1}{2} \) (Area of rectangle) the remaining portion of rectangle containing two triangles

BAE and CDE = BEC = 64 cm²

So, the area of ΔBEC is equal to the sum of the area of ΔBAE and ΔCDE.

Haryana Board Class 7 Maths Solutions For Chapter 9 Multiple Choice Question and Answers

1. 1 Hectare =

1. 100 m²
2. 1000 m²
3. 1000 mm²
4. 10 m²

Answer: 3

2. Side of a square is 50 cm find its area

1. 2500 cm²
2. 2000 cm²
3. 2500 cm
4. 200 cm

Answer: 1

3. The perpendicular dropped on that side from the opposite vertex is known as

1. median
2. height
3. side
4. length

Answer: 2

4. If the area of a parallelogram is 24 cm2 and the base is 4 cm then its height is

1. 4 cm
2. 6 cm
3. 48 cm
4. 96 cm

Answer: 2

5. Diameter of a circle is 10 cm. Its radius is

1. 20 cm
2. 10 cm
3. 5 cm
4. 40 cm

Answer: 3

6. If the area of a circle is 2464 m² find its diameter.

1. 14 m
2. 28 m
3. 56m
4. 45 m

Answer: 3

7. The circumference of a circle is 44 m. What is its area?

1. 44 cm²
2. 154 cm²
3. 164 cm²
4. 144 cm²

Answer: 2

8. Two sides of a right-angled triangle are 100 cm and 8.6 cm find its area.

1. 340 cm²
2. 530 cm²
3. 430 cm²
4. 240 cm²

Answer: 3

9. Find the altitude of a triangle whose base is 24 m and area 672 cm².

1. 56 cm
2. 4 cm
3. 26 cm
4. 36 cm

Answer: 1

10. Find the area of the triangle whose base is 14 cm and height is 650 cm

1. 3550 cm²
2. 4550 cm²
3. 2550 cm²
4. 5550 cm²

Answer: 2

11. If the perimeter of a semi-circle is 144 cm. What is its area?

1. 1132 cm²
2. 1432 cm²
3. 1232 cm²
4. 1332 cm²

Answer: 3

12. If each side of a square is 1 m which of the following is its area?

1. 100 cm²
2. 1000 cm²
3. 10000 cm²
4. 100000 cm²

Answer: 3

13. The sides of a triangle are 3 cm, 4 cm, and 5 cm respectively then the perimeter is

1. 10 cm
2. 12 cm
3. 20 cm
4. 15 cm

Answer: 2

14. If the side of an equilateral triangle is 6 cm then its perimeter is

1. 15 cm
2. 12 cm
3. 18 cm
4. 24 cm

Answer: 3

15. If the side of a right-angled isosceles triangle is 2 m then its area is

1. 4 m²
2. 6 m²
3. 5 m²
4. 2 m²

Answer: 4

16. The diagonals of a rhombus are 8 cm and 12 cm then its area is

1. 64 sq.cm
2. 40 sq.cm
3. 48 sq.cm
4. 70 sq.cm

Answer: 3

17. If the base of an isosceles right triangle is 30 cm then its area is

1. 300 sq.cm
2. 400 sq.cm
3. 450 sq.cm
4. 500 sq.cm

Answer: 3

18. If the diameter of the circle is 52 cm then its radius is

1. 26 cm
2. 27 cm
3. 28 cm
4. 29 cm

Answer: 1

19. If the radius of a circle is 12 m then the circumference of a circle is

1. 20πm
2. 24πm
3. 48πm
4. 42πm

Answer: 2

20. Choose the correct matching.

1) Circumference of circle              (  )    1/2 bh

2) Area of circle                              (  )      l x b

3) Area of triangle                          (  )     2Πr

4) Area of rectangle                       (  )     Πr2

                                                        (  )  \( \frac{\pi r^2}{2} \)

1. 1 – c,2 – d,3 – a,4- b
2. 1 – e,2 – a,3 – b,4- d
3. 1 – a,2 – c,3 – b,4- d
4. 1 – e,2 – b,3 – c,4- a

Answer: 1

21. The area of a rhombus is 60cm2 and one of its diagonals is 8 cm find the other diagonal.

1. 10 cm
2. 15 cm
3. 20 cm
4. 25 cm

Answer: 2

22. If the area of a rectangle is 144 m2 then its length and breadth are

1. 18 m, 8 m
2. 16 m, 9m
3. 24 m, 6m
4. All of them

Answer: 4

23. The perimeter of a square is 1 meter then its side is…..

1. 10 cm
2. 25 cm
3. 20 cm
4. 50 cm

Answer: 2

24. The product of length of two diagonals of a rhombus is 90 cm2 then its area is……

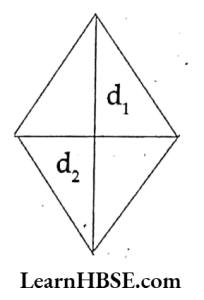
1. 90 cm²
2. 45 cm²
3. 180 cm²
4. 135 cm²

Answer: 2

25. Choose the correct matching.

1. i-c,ii-b,iii-a
2. i-a,ii-c,iii-b
3. i-a,ii-b,iii-c
4. i-c,ii-a,iii-b

Answer: 2

26. ABCD is a rectangle. The ratio of the areas of ABCD and AED is………..

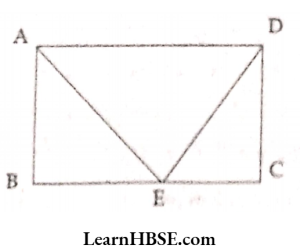
1. √2:1
2. 2:1
3. 3:1
4. 3:√2

Answer: 2

27. If the outer radius of a circular path is R and its width is W, then its area in sq. units is

1. Π(2R-W) W
2. Π(R-W)W
3. Π(R+W)W
4. Π(R+W)(R-W)

Answer: 1

28. If the radii of two circles are in the ratio 9:16 then the ratio of their areas is

1. 81:256
2. 265:84
3. 3:4
4. 4:3

Answer: 1

29. If the perimeter of a circle is 16 times to the perimeter of square then the ratio of radius to the side is……….

1. 112:11
2. 11:112
3. 11: 128
4. 256: 11

Answer: 1

30. Statement – 1: If r is a radius of a circle then 2itr is the circumference of the cird.

Statement -II: If the side of the square is 14cm then the ratio of the square and circle perimeter is 14: 11

1. Both statements are true.
2. Both statements are false.
3. Statement – 1 is true statement – II is false.
4. Statement – 1 is false statement -II Is true.

Answer: 1

31. Statement – 1: If the inner and outer radii of circular rings arc 3.5 m and 7 m then area of the ring is 1185 m².

Statement -II: Area of the ring whose inner and outer radii are r, R is Π(R + r)(R – r) sq. units.

1. Both statements are true. Statement – II is the correct explanation of statement -I.
2. Both statements are true. Statement -II is not correct explanation statement-I.
3. Statement – 1 is true, statement – II is false.
4. Statement – I Is false, statement II is true.

Answer: 4

32 Base and height of a parallelogram are 6 cm and 13 cm respectively. Its area is

1. 39 sq.m
2. 78 sq.m
3. 82 sq.m
4. 38 sq.m

Answer: 2

33. Area of the parallelogram is 1470 cm2. Its base is 49 cm then the corresponding height is

1. 42 cm
2. 21cm
3. 30 cm
4. 32 m

Answer: 3

34. If the inner and outer radii of circular rings are 4m and 8m then the area of the ring is……..m².

1. 148
2. 150.86
3. 160.81
4. 140.72

Answer: 2

35. In ΔABC, ∠A = 90. AB=5 cm; AC= 12 cm; BC=13 cm, then area of ΔABC is

1. 30 cm²
2. 31.5 cm²
3. 78 cm²
4. 60 cm²

Answer: 1

36. The diagonals of a rhombus are li2 cm and 16 cm then its area is……square cms.

1. 192
2. 96
3. 126
4. 108

Answer: 2

37. The circumference of a circle whose radius is 4.2 cm

1. 27.2 cm
2. 26.4 cm
3. 18.6 cm
4. 13.2 cm

Answer: 2

38. If the circumference of a circle is 264 cm, then its radius is

1. 36 cm
2. 40 cm
3. 42 cm
4. 38 cm

Answer: 3

39. A road roller makes 200 rotations in covering 2200m then the radius of the road roller is

1. 1.75 m
2. 1.25 m
3. 2.15 m
4. 2.25 m

Answer: 1

40. In a rhombus ABCD, ∠A = 60°, AB = 6 cm then the length of the diagonal BD in cm is

1. 12
2. 9
3. 6
4. 3

Answer: 3

41. In the adjacent figure side of a square is 7cm. A circle is inscribed in the square. The perimeter of the circle is

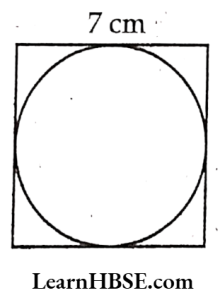
1. 11 cm
2. 44 cm.
3. 22 cm
4. 28 cm

Answer: 3

Observe the table and answer the following questions. (42 – 44)

42. What is the formula for area of a rectangle?

1. 2(l +b)
2. l x b
3. l ÷ b
4. l + b

Answer: 2

43. What are the dimensions here?

1. length
2. breadth
3. A or B
4. A and B

Answer: 4

44. What information does this table give us?

1. It gives formula for area of rectangle
2. It gives formula for perimeter of rectangle
3. A and B
4. None

Answer: 3

45, What In the length of QS?

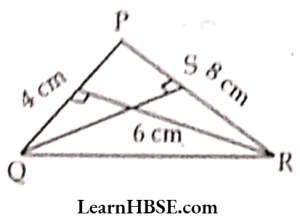
1. 4 cm
2. 3 cm
3. 2 cm
4. 6 cm

Answer: 2

46. Find the bane of n triangle whose area is 220 cm2 and height is 11 cm.

1. 40 cm
2. 50 cm
3. 60 cm
4. 70 cm

Answer: 1

Read the above table and answer the following questions (47 – 49)

47. About which area this table tells us

1. Parallelogram
2. Rectangle
3. Square
4. Rhombus

Answer: 4

48. What are the values of a and x?

1. 96 cm², 6 cm
2. 6 cm, 96 cm²
3. 30 cm², 6 cm
4. 36 cm², 6 cm

Answer: 1

49. What is the formula for area of a rhombus?

1. bh
2. \( \frac{1}{2} \mathrm{bh} \)
3. \( \frac{1}{2} \mathrm{~d}_1 \mathrm{~d}_2 \)
4. l x b

Answer: 3

50. If the circumference is 30cm more than the diameter of the circle find the radius of the circle.

1. 7 cm
2. 8 cm
3. 9 cm
4. 10 cm

Answer: 1

51. Area of a semi-circle is 77cm². Its perimeter is equal to

1. 35 cm
2. 44 cm
3. 42 cm
4. 36 cm

Answer: 4

52. Area of the parallelogram is 1470 cm².Its base is 30 cm then the corresponding height

1. 42 cm
2. 21cm
3. 49 cm
4. 32 cm

Answer: 3

53. What is the length of DL if AB = 13 cm and area of parallelogram is 156 cm² ?

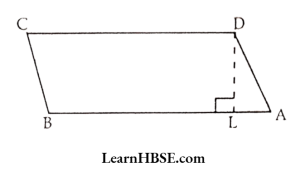
1. 13 cm
2. 12 cm
3. 14 cm
4. 15 cm

Answer: 2

54. What is the area of quadrilateral?

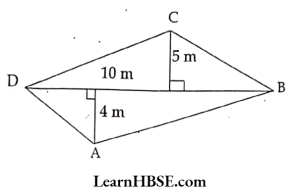
1. 25 m²
2. 35 m²
3. 45 m²
4. 55 m²

Answer: 3

55. What is the difference of circumferences of the circles shown ?

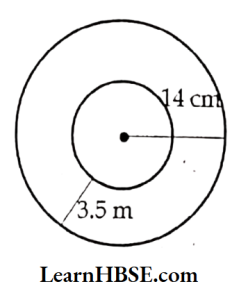
1. 22 cm
2. 33 cm
3. 44 cm
4. 66 cm

Answer: 1

Haryana Board Class 7 Maths Solutions For Chapter 9 Fill in the blanks:

56. Perimeter of a regular polygon is……………..

Answer: Number of sides x Length of one side

57. All congruent triangles are equal in…………

Answer: area

58. The distance around a circular region is known as its ………

Answer: circumference

59. The perimeter of a parallelogram whose base is 5 units and height 3 units is………

Answer: 16 units

60. The area of a triangle is 36 cm² and the height is 3 cm. Its base is………..

Answer: 24 cm

Haryana Board Class 7 Maths Solutions For Chapter 9 Match the following:

61. Figure                             Area

1. Square                (   ) A) Length x Breadth

2. Rectangle           (   ) B) Base x Height

3. Triangle              (   ) C)r²

4. Parallelogram    (   ) D) (Side)²

5. Circle                  (   ) E) 1/2 x base X height

Answer: 1. D 2. A 3. E . 4. B 5. C

62.

1. Perimeter of a square                                                                                    (  ) A) π x diameter

2. Perimeter of a rectangle                                                                               (  ) B) 20 cm

3. Circumference of a circle                                                                              (  ) C) 4 X Side

4. Area of a rectangular sheet is 500 cm2, length is 25 cm its breadth is    (  ) D) 6m²

5. Base of a triangle is 3 cm, height is 4 cm its area is                                   (  ) E) 2 (Length + Breadth)

Answer: 1. C 2. E 3. A 4. B 5. D