Haryana Board Class 7 Maths Solutions For Chapter 10 Algebraic Expressions
Key Concepts
- Introduction:
Expressions are a central concept in algebra. x + 3, y- 5, 4x + 5,10y- 5 are some simple algebraic expressions. - Variable:
A variable can take various values. Its value is not fixed. We use the letters x, y, l, m ………..etc. to denote variables. - Constant:
A constant has a fixed value.
Examples: 4, 100, -17 etc.
- Algebraic Expression:
A number of combination of numbers using the signs of fundamental operations is called an expression.
We combine variables and constants to make algebraic expressions. For this we use the operations of addition, subtraction, multiplication, and division.
Examples: 4x + 5, 10y – 20.
Look at how the following expressions are obtained:- x²,
- 2y²,
- 3x²- 5,
- xy,
- 4xy+7
- The expression x2 is obtained by multiplying the variable x by itself.
x × x = x². It is commonly read as squared
x × x × x=x³. It is read as ‘x’ cubed.
x, x², x³……..are all algebraic expressions obtainedfrom x. - The expression 2y² is obtained from y = 2y²= 2 × y × y. Here by multiplying y with y, we obtain y² and then we multiply y² by the constant 2.
- In 3x² – 5, we first obtain x² and multiply it by 3 to get 3x². From 3x², we subtract 5 to finally arrive at 3x²- 5.
- In xy, we multiply the vanable x with another variable y. Thus, x xy = xy.
- In,4xy + 7, we first obtain xy, and multiply it by 4 to get 4xy one add 7 to 4xy to get the expression.
- The expression x2 is obtained by multiplying the variable x by itself.
- Terms of an expression:
The expression is separated by ‘+’ or ‘ – ‘ into several parts each part along with its sign is known as the term of the expression.
Example: 8x²- 6xy. The terms in this expression are 8x² and- 6xy.
Solutions To Try These
Describe how the following expressions are obtained.
7xy + 5,x²y, 4X²- 5x
Solutions:
7xy + 5: We multiply the variable x with another variable y to obtain xy and then multiply by the constant 7 to get 7xy. Adding 5 to 7xy we obtain 7xy + 5.
x²y: Multiply the variable x with itself to obtain x² and then multiply with y to get x²y.
4x²- 5x: Multiply the variable x with itself to obtain x² and. then multiply with 4 to get 4x².
Multiply the variable x with a constant 5 to get 5x. Then subtract 5x from 4x² to get 4x²-5x
Solutions To Try These
1. What are the terms in the following expressions? Show how the terms are formed. Draw a tree diagram for each expression :
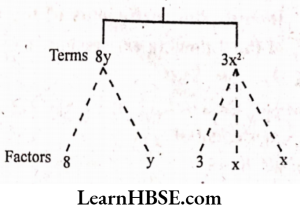
- 8y + 3x²,
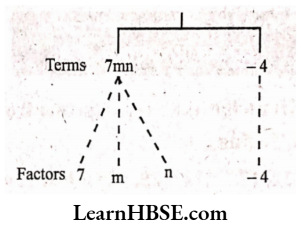
- 7mn- 4,
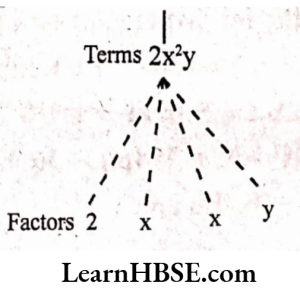
- 2x²y.
1) 8y + 3x²
Solution: Terms: 8y, 3x²
The term 8y is formed by multiplying the variable y by 8.
The term 3x² is formed by multiplying 3, x, and x.
Tree diagram
Expression: 8y+3x²
2) 7mn- 4
Solutions: Terms: 7mn,- 4
The term 7mn is formed by multiplying 7, m, and n. The term – 4 is a constant.
Tree diagram
Expression: 7mn- 4
HBSE Class 7 Algebraic Expressions Solutions Ex 10.1 Solved
Solution: Terms: 2x²y
The term 2x²y is formed by multiplying
2, x, x and y
Tree diagram
Expression: 2x²y
Haryana Board Class 7 Maths Algebraic Expressions solutions
2. Write three expressions each having 4 terms.
Solution:
(1) 4x²- 3xy + 4x + 13
(2) 3x²- 5y²-+ 7 xy + 8
(3) 5x³- 5x²- 5x- 5
Solutions To Try These
Identify the coefficients of the terms of the following expressions :
(1) 4x-3y
Solutions: 4 is the coefficient of x; – 3 is the coefficient of. y.
2) a + b + 5
Solution: The coefficient of a and b is 1.
3) 2y + 5
Solution: The coefficient of y is 2.
4) 2xy
Solution:
The coefficient of xy is 2.
The coefficient of x is 2y.
The coefficient of y is 2x.
Solutions To Try These
Group the like terms together from the following: 12x, 12, -25x, -25, -25y, 1, x, 12y, y
Solution:
Like terms are 12x, -25x, x
-25y, 12y,y
12, -25, 1
Solutions To Try These
Classify the following expressions as a monomial, a binomial or a trinomial: a, a + b, ab + a + b, ab + a +b- 5, xy, xy + 5, 5x²- x + 2, 4pq – 3q + 5p, 7, 4m- 7n + 10, 4mn + 7.
Solution:
Monomials: a, xy, 7
Binomials: a + b, xy + 5, 4mn + 7
Trinomials : ab + a + b, 5x²- x + 2,
4m- 7n + 10, 4pq- 3p + 5p
Polynomial: ab+a+b-5
Haryana Board Class 7 Maths Solutions For Chapter 10 Exercise-10.1 :
1. Get the algebraic expression in the following cases using variables, constants, and arithmetic operations.
- Subtraction of z from y. → y- z
- One-half of the sum of numbers, x and \( y \rightarrow \frac{1}{2}(x+y) \)
- The number z multiplied by itself. → z²
- One-fourth of the product of numbers p and q.→\( \frac{1}{4} \mathrm{pq}\)
- Numbers x and y both squared and added. x²+, y²
- Number 5 added to three times the product of numbers m and n. → 3mn + 5
- Product of numbers y and z subtracted from 10. → 10- yz
- Sum of numbers a and b subtracted from their product→ ab-(a + b)
2. (1) Identify the terms and their factors in the following expressions. Show the terms and factors by tree diagrams.
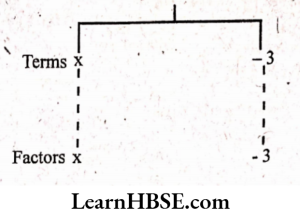
1) x- 3
Solution:
Expression: x-3
2) 1+x + x²
Solution: Expression: 1 + x + x²
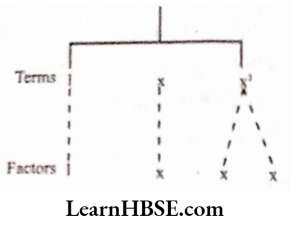
3) y – y³
Solution:
Expression: y – y³
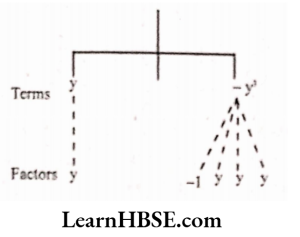
HBSE Class 7 Maths Chapter 10 Get Algebraic Expressions
3) 2x²y
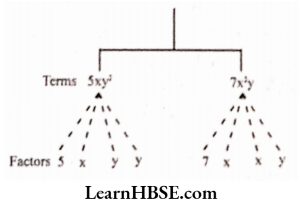
4) 5xy² + 7x²y
Solution:
Expression: 5xy²+ 7x²y
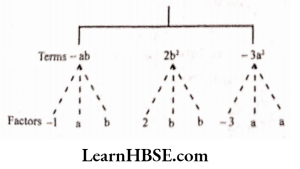
5) -ab + 2b²-3a²
Solution:
Expression: -ab + 2b²-3a²
(2) Identify terms and factors in the expressions given below:
1) – 4x + 5
Solution:
Terms: – 4x, 5
Factors : – 4, x; 5
2) – 4x + 5y
Solution:
Terms: – 4 x; 5y
Factors: – 4, x; 5, y
3) 5y + 3y²
Solution:
Terms: 5y, 3y²
Factors: 5, y; 3, y, y
4) xy +2x²y²
Solution:
Terms: xy; 2x²y²
Factors: x, y; 2, x, x, y, y
5) pq + q
Solution:
Terms: pq, q
Factors : p, q; q
6) 1.2ab – 2.4b + 3.6a
Solution:
Terms: 1.2ab; -2.4b; 3.6a
Factors: 1.2, a, b; -2.4, b; 3.6, a
7) \( \frac{3}{4} x+\frac{1}{4} \)
Solution:
Terms: \( \frac{3}{4} x ; \frac{1}{4} \)
Factors: \( \frac{3}{4}, x ; \frac{1}{4} \)
8) 0.1p² + 0.2q²
Solution:
Terms: 0.1p², 0.2q²
Factors: 0.1, p, p; 0.2, q, q
3. Identify the numerical coefficients of terms (other than constants) in the following expressions:
1) 5 – 3t²
Solution:
Term which Is not constant is -3t²
Numerical coefficient is -3
2) 1 + t + t²+ t³
Solution:
Terms which are not constant are t, t²,t³
Numerical coefficients: 1, 1,1
3) x + 2xy + 3y
Solution:
Terms which are not constant are x, 2xy,3y
Numerical coefficients: 1, 2, 3
HBSE 7th Class Algebraic Expressions Word Problems Solutions
4)100m + 1000n
Solution:
Terms which are not constant are 100m 1000n.
Numerical coefficients: 100, 1000
5) – p²q² + 7pq
Solution:
Terms which are not constant are -p²q²;7pq
Numerical coefficients: -1, 7
6) 1.2a + 0.8b
Solution:
Terms which are not constant are 1.2a; 0.8b
Numerical coefficients: 1.2, 0.8
7) 3.14r²
Solution:
Term: 3.14r²
Numerical coefficient is 3.14
How to simplify algebraic expressions Class 7 HBSE
8) 2(l+ b)
Solution:
2(l + b) =2l+ 2b
Terms: 2l; 2b
Numerical coefficients: 2, 2
9) 0.1y + 0.01y²
Solution:
Terms: 0.1y + 0.01y²
Numerical coefficients: 0.1; 0.01
4. a) Identify terms which contain x and give the coefficient of x.
1) y³x + y
Solution:
Term which contain x is y²x
Coefficient of x is y²
2) 13y² – 8yx
Solution:
Term which contain x is -8 yx
Coefficient of x is- 8y
3) x+y + 2
Solution:
Term which contain x is x
Coefficient ‘of x is 1
4) 5 + z + zx
Solution:
Term which contain x is zx
Coefficient of x is z
5) 1 + x + xy
Solution:
Term which contain x are x, xy
Coefficients of x are 1, y
6) 12xy² + 25
Term which contain x is 12xy²
Coefficient of x is 12y².
7) 7x + xy²
Solution:
Terms which contain x are 7x and xy²
Coefficients of x are 7 and y²
2) Identify terms which contain y² and give the coefficient of y².
1) 8-xy²
Solution:
Term which contain y² is – xy²
Coefficient of y² is – x.
2) 5y² + 7x
Solution:
Term which contain y² is 5y²
Coefficient of y² is 5
3) 2x²y – 15xy² + 7y²
Solution:
Terms which contains y² is -15xy²; 7y²
Coefficients of y² are -15x; 7
5. Classify into monomials, binomials and trinomials.
- 4y-7z
- y²
- x + y- xy
- 100
- ab – a – b
- 5 – 3t
- 4p²q-4pq²
- 7mn
- z²- 3z + 8
- a² + b²
- z² + z
- 1 + x + x²
Solution:
Monomials: (2) y², (4)100, (8) 7 mn
Binomials: (1) 4y- 7z,(6) 5 -3t, (7) 4p²q -4pq², (10) a² + b², (11) z² + z
Trinomials : (3) x + y- xy, (5) ab- a-b, (9) z²- 3z + 8, (12)1+ x + x²
6. State whether a given pair of terms is of like or unlike terms.
1) 1,100
Solution: 1, 100 are like terms.
2) \( -7 x, \frac{5}{2} x \)
Solution: \( -7 x, \frac{5}{2} x \) are like terms.
3) -29x, -29y
Solution: -29x, -29y are unlike terms.
4) 14xy, 42yx
Solution: 14xy, 42yx are like terms.
5) 4m²p,4mp²
Solution: 4m²p, 4mp² are unlike terms.
7) 12xz, 12x²z²
Solution: 12xz, 12x²z² are unlike terms.
7. Identify like terms in the following:
1) -xy², – 4yx², 8x², 2xy², 7y, -11x², -100x,-11yx, 20x²y,- 6x², y, 2xy, 3x
Solution:
Like terms are:-
xy², 2xy²;- 4yx², 20x²y;- 8x², -6x², – 11x²; 7y, y; -100x, 3x; -11yx, 2xy
2)10pq, 7p, 8q, -p²q², -7qp, – 100q, -23,12q²p², -5p², 41, 2405p, 78qp,13p²q, qp², 701p²
Solution:
Like terms are :
10pq, -7qp, 78qp; 7p, 2405p; 8q, -100q; -p²q²,12qy;- 23, 41; -5p², 701p²; 13p²q, qp²
Haryana Board Class 7 Maths Solutions For Chapter 10 Exercise-10.2
1. If m = 2, find the value of:
1) m-2
Solution: m-2
Putting m = 2 in m- 2
we get m-2=2-2=0
2) 3m -5
Solution: Putting m = 2 in 3m- 5
we get 3m-5 = 3 x 2-5
=6-5=1
3) 9 -5m
Solution: 9 -5m
Putting m = 2 in 9- 5m
we get 9- 5m = 9- (5 x 2) ,
= 9- 10 = -1
4) 3m² -2m -7
Solution:
Putting m = 2 in 3m²- 2m- 7 we get
3m²- 2m- 7 = 3(2)² -2(2) -7
=3 x 4-2 x 2-7
=12-4-7
=12-11 =1
5) \( \frac{5 m}{2}-4 \)
Solution:
Putting m = 2 in \( \frac{5 m}{2}-4 \)
we get
\( \frac{5 m}{2}-4=\frac{(5 \times 2)}{2}-4 \)=5-4=1
2. If p- – 2 find the value of:
(1) 4p + 7
Solution:
Putting p = -2 in 4p + 7 we get
4p + 7 = 4(-2) + 7
=-8+7
=-1
2) – 3p² + 4p + 7
Solution:
Putting p =- 2 in -3p² + 4p + 7 we get
– 3p² + 4p + 7 = – 3(-2)²+ 4 (-2) + 7
= (-3 x 4) + (-4 x 2) + 7
=-12 – 8 + 7
= -20 + 7 = -13
Simplifying Algebraic Expressions Class 7 HBSE Solved Examples
3) -2p³ – 3p² + 4p + 7
Solution:
Putting p = -2 in -2p³- 3p² + 4p + 7 we get
get
-2p³- 3p² + 4p + 7 =
-2 (-2)³- 3 (-2)² + 4 (-2) + 7
=-2 x (-8) -3 x 4-4 x 2 + 7
=16-12-8 + 7
= 23 – 20 = 3
Practice Problems Algebraic Expressions Class 7 Haryana Board with Substitution
3. Find the value of the following expressions, when x = -1:
1) 2x-7
Solution:
Putting x = -1 in 2x- 7 we get
2x- 7 = 2(-1) -7
= -2-7
= -9
2) -x + 2
Solution:
Putting x = -1 in -x + 2 we get
= x + 2 = – (-1) + 2
=1 + 2
= 3
3) x² + 2x +1
Solution:
Putting x = -1 in x² + 2x +1 we get
x²+ 2x +1 = (-1)² + 2 (-1) +1
=1-2+1 =2-2=0
4) 2x²- x- 2
Solution:
Putting x = -1 in 2x²- x- 2 we get
2x²- x- 2 = 2(-1)²- (-1)- 2
=2+1-2 =3-2=1
4. If a = 2 b = -2, find the values of:
1) a² + b²
Solution:
Putting a = 2;b = -2 in a² + b² we get a² + b² = (2)² + (-2)²
-4+4=8
2) a² + ab + b²
Solution: Putting a = 2; b = -2in a² + ab + b² we get
a²+ ab + b²
= (2)² + 2(-2) + (-2)²
=4-4+4
=8-4=4
3) a²- b²
Solution:
Putting a = 2; b = -2 in a²- b² we get
a²-b²=(2)²-(-2)²
=4-4=0
5. When a = 0, b = -1, find the value of the given expressions:
1) 2a + 2b
Solution:
Putting a =0; b = -1 in 2a + 2b we get
2a + 2b = 2(0) +2(-1)
= 0- 2 = -2
Addition and subtraction of algebraic expressions Class 7
2) 2a² + b²+1
Solution:
Putting a = 0; b= -1 in 2a²+ b² +1 we get
2a² + b² +1 = 2(0)² + (-1)² +1
=0+1 +1 =2
3) 2a²b + 2ab² + ab
Solution:
Putting a = 0;b = -1 in 2a²b + 2ab² + ab we get
2a²b + 2ab² + ab =
2(0)² (-1) + 2(0) (-1)² +0(-1)
0+0+0=0
4) a² + ab + 2
Solution:
Putting a = 0;b =-1 in a² + ab+ 2 we get
a² + ab + 2 = (0)² + 0 (-1) + 2
=0+0+2=2
6. Simplify the expressions and find the value if x is equal to 2
1) x + 7 + 4 (x- 5)
Solution:
x + 7 + 4 (x- 5)
= x + 7 + 4x-20
= x + 4x + 7- 20
= 5 x- 13
Putting x = 2 in 5x- 13 we get
5x- 13 = 5(2) -13
=10-13
=- 3
2) 3(x + 2) + 5x- 7
Solution:
3(x + 2) + 5x- 7
= 3x + 6 + 5x- 7
= 3x + 5x + 6 – 7
=8x-1
Putting x = 2 in 8x-1 we get
8x-1 = 8(2) -1
=16-1=15
3) 6x + 5 (x- 2)
Solution:
6x + 5(x- 2)
= 6x + 5x- 10
=11x -10
Putting x = 2 in 11x- 10 we get
11x- 10 = 11(2) – 10
= 22-10 =12
Important Concepts Algebraic Expressions Class 7 HBSE NCERT Based
4) 4(2x- 1) + 3x +11
Solution: 4(2x- 1) + 3x + 11
= 8x- 4 + 3x +11
= 8x + 3x +11 – 4
=11x + 7
Putting x = 2inllx + 7 we get
11x + 7 = 11(2) + 7= 22 + 7= 29
7. Simplify these expressions and find their values if x = 3, a = -1, b = -2.
1) 3x- 5 – x + 9 ‘
Solution: 3x-5-x + 9
=3x-x-5 + 9 = 2x + 4
Putting x = 3 in 2x + 4 we get
2x + 4 = 2(3) + 4
= 6 + 4 = 10
2) 2- 8x + 4x + 4
Solution: 2-8x + 4x + 4
= -8x + 4x + 4 + 2
= -4x + 6
Putting x = 3 in- 4x + 6 we get
-4x + 6 = -4 (3) + 6
= -12 + 6 = -6
3) 3a + 5 – 8a +1
Solution: 3a + 5- 8a +1
= 3a- 8a + 5 +1
= -5a + 6
Putting a = -1 in -5a + 6 we get
-5a + 6- -5 (-1) + 6
= 5 + 6 =11
4) 10- 3b – 4 – 5b
Solution: 10-3b-4-5b
= -3b- 5b + 10- 4
= -8b + 6
Putting b = -2 in – 8b + 6 we get
– 8b + 6 = -8 (-2) + 6
= 16 + 6 = 22
5) 2a -2b -4 -5 + a
Solution:
2a-2b-4-5 + a
= 2a + a -2b- 4- 5
= 3a- 2b- 9
Putting a = -1; b = -2 in 3a – 2b- 9 we get
3a -2b- 9 = (3 (-1) -2 (-2) -9)
= -3 + 4- 9 = – 12 + 4
= -8
8. (1) If z = 10 find the value of z³ – 3(z- 10)
Solution:
z³ – 3 (z- 10)
Putting z = 10 in z³- 3 (z- 10) we get
z³- 3(z- 10) = (10)3- 3(10- 10)
= 1000- 3 x 0
=1000- 0 = 1000
Substituting Values in Algebraic Expressions Class 7 Haryana Board Solutions Ex 10.3
2) If p = -10 find the value of p²-2p -100
Solution:
p²- 2p -100
Putting p = -10 in p²- 2p -100 we get
p²- 2p -100 = (-10)² – 2(-10) – 100
= 100 + 20-100
=120-100 = 20
9. What should be the value of ‘a’ if the value of 2x² + x – a equals to 5, when x = 0 ?
Solution:
2x²+ x-a = 5
Putting x = 0 in 2 x²+ x- a = 5 we get ,
2(0)² + 0-a = 5
-a = 5 1
a =- 5
10. Simplify the expression and find its value when a = 5 and b =- 3.
2(a² + ab) + 3 – ab
Solution:
2(a² + ab) + 3- ab = 2a²+ 2ab + 3- ab
= 2a² + 2ab- ab + 3
= 2a² + ab + 3
Putting a = 5 and b = -3 in 2a²+ ab + 3
2a² + ab + 3 = 2(5)² + (5) (-3) + 3
= 2×25-15 + 3
= 50-15 + 3
= 53-15 = 38
Haryana Board Class 7 Maths Solutions For Chapter 10 Very Short Answer Questions
1. Define
- Monomial
- Binomial
- Trinomial
Solution:
- An expression with only one term is called a monomial.
- An expression which contain two unlike terms is called a binomial.
- An expression which contain three terms is called a trinomial.
2. Define polynomial.
Solution: In general an expression with one or more terms is called a polynomial.
3. Give examples to each
- Monomial
- Binomial
- Trinomial.
Solution:
- Monomial: – 3x,- 5m
- Binomial : -2x + y,z-3
- Trinomial: -a+b+3,x+y+z
4. Find the value of the expression a³- b³ for a = 3;b = 2
Solution:
Substituting a =3;b = 2 in a³- b³ we get
(3)³- (2)³ = 3 x 3 x 3 – 2 x 2 x 2
= 27-8 =19
5. Simplify the expression 4 (2x-1)+3x +11
Solution:
4 (2x-1)+ 3x + 11 =- 8
= 4 x 2x- 4 x1 + 3x + 11
= 8x-4 + 3x +11
= 8x + 3x + 11 – 4
=11x + 7
Important formulas for algebraic expressions Class 7
6. Write 3 algebraic expressions with 3 terms each.
Solution:
2x² + 3x + 5
px² + q x + r
ax² + bx + c
7. Find the value of the expression – 9x if x = -3.
Solution:
Given x = -3
= -9x
= -9(-3)
= 27
8. Write the expression whose value is equal to -9 when x = -3.
Solution: -9
= -3×3
= (-3)3
= (x)3 [∵Given x = -3]
= 3x
The required expression is 3x.
Haryana Board Class 7 Maths Solutions For Chapter 10 Short Answer Questions
9. Identify the expressions given below as monomial, binomial, trinomial, and polynomial.
1) 5x² + y + 6
Solution:
In this expression three unlike terms.
So, it is Trinomial.
2) 3xy
Solution: In this expression, only one term
So, it is Monomial.
3) 5x²y + 6x
Solution: In this expression, two unlike terms
So, it is Binomial.
4) a +4x-xy + xyz
Solution:
In this expression, more than one, unlike terms. So, it is polynomial.
10. Identify and write the like terms in each of following groups.
1) a², b², – 2a², c², 4a
Solution:
a², b², – 2a², c2, 4a are unlike terms
Here, a²,- 2a², are like terms
2) 3a, 4xy, – yz, 2zy •
Solution:
3a, 4xy, – yz, 2zy are unlike terms.
Here, – yz, 2zy are like terms.
3) -2xy², x²y, 5y²x, x²z
Solution:
–2xy², and 5y²x, are like terms.
4) 7p, 8pq, -5pq, -2p, 3p
Solution:
7p, 8pq, -5pq, -2p, 3p are unlike terms.
8pq, -5pq, are like terms
7p, -2p, 3p are like terms.
11. Find the value of the following monomials, if x =1.
Given x = 1.
1) -x
Solution: Consider -x
= -(1)
= -1
2) 4x.
Solution: Consider 4x
= 4(1)
= 4
3) -2X²
Solution: Consider
-2x²
– -2(1)²
= -2(1)
= -2
12. Simplify and find the value of 4x + x- 2x² + x-1 when x = -1.
Solution:
Consider
4x + x – 2x² + x-1
=-2x²+ (4 +1 + 1)x-1
= -2x² + 6x- 1
But given x = -1
= -2(-1)² + 6(-1) -1
= -2(1) -6-1
= -9
13. Write the expression
5x² – 4 – 3x² + 6x + 8 + 5x – 13 in its simplified form. Find its value when x = -2.
Solution:
5x²- 4- 3x² + 6x + 8 + 5x- 13
= (5x²- 3x²) + (6x + 5x) + (8- 4- 13)
= (5 – 3)x² + (6 + 5)x + (8 – 17)
= 2x² +11x – 9
But given x = -2
= 2(-2)² + 11(-2) – 9
= 2(4) – 22- 9
= 8-22-9
= 8-31
= -23
Key Questions in Algebraic Expressions Ex 10.3 for Class 7 HBSE
14. If x = 1, y = 2 find the values of the following expressions.
Given x =1,y = 2
1) 4x-3y + 5
Solution:
4x- 3y + 5
= 4(1) -3(2) +5
= 4-6+5
=’ 9-6 = 3
2) x² + y²
Solution:
Consider
x² + y²
= (1)² +(2)²
= 1+ 4
= 5
3) xy + 3y-9
Solution: Consider
xy + 3y- 9
= (1) (2) +3(2) -9
= 2+6-9
= 8-9 = -1
15. Group the like terms together 12x, 12, 25x, – 25, 25y, 1, x, 12y, y, 25xy, 5x²y, 7xy²,2xy, 3xy², 4x²y.
Solution:
Group A 12x, 25x, x
Group B 25y,12y,y
Group C 25,xy, 2xy
Group D 5x²y, 4x²y
Group E 7xy², 3xy²
Group F 12,1,-25
Haryana Board Class 7 Maths Solutions For Chapter 10 Long Answer Questions
16. State true or false and give reasons for your answer.
1) 7x² and 2x are unlike terms.
Solution: It is True.
Both terms contain the same variable x.
However, their exponents are not same.
In the first term, the exponent of x is
2 and in the second term it is 1.
2) pq² and -4pq² are like terms
Solution: It is True.
Both terms contain the same variables p and q. However, the exponent of p is 1, and exponent of q is 2.
Multiplication of polynomials Class 7 Haryana Board
3) xy, -12x²y and 5xy² are like terms.
Solution: It is false.
The above terms contain the same variables x and y. However, their exponents are not the same.
In the first term, the exponent of x is 1, and second it is 1.
In the second term, the exponent of x is 2, and second it is 1.
In the third term, the exponent of x is ,1 and second it is 2.
17. State whether the algebraic expression given below is monomial, binomial, trinomial or polynomial.
1) y²
Solution: Monomial.
2) 4y-7z
Solution: Binomial
3) 1+x + x²
Solution: Trinomial
4) 7mn
Solution: Monomial
5) a² + b²
Solution: Binomial
6) 100 xyz
Solution: Monomial,
7) ax + 9
Solution: Binomial
8) p²- 3pq +r
Solution: Trinomial
9) 3y² – x²y² + 4x
Solution: Trinomial
10) 7x²-2xy + 9y²-11
Solution: Polynomial
Haryana Board Class 7 Maths Solutions For Chapter 10 Multiple Choice Answer Questions
Choose the correct answers:
1. In the expression 4x + 5 variable is
- 4
- 5
- x
- x+5
Answer: 3
2. The coefficient of y in 2y + 5 is
- 2
- 2y
- 5
- y + 5
Answer: 1
3. The nth term of the number pattern 11, 21, 31, 41. is
- 10n
- n + 10
- 10 (n + 1)
- 10n +1
Answer: 4
4. What is the coefficient of xin 6xy² + 7y is
- 6
- y2
- 6y²
- 7
Answer: 3
5. The value of 4z +1 for z = 2 is
- 5
- 1
- 8
- 9
Answer: 4
6. Which type of expression is 2x² + 3x +1 ?
- monomial
- binomial
- trinomial
- multinomial
Answer: 3
7. How many terms are there in this expression 4x² y4 z?
- 1
- 2
- 3
- 4
Answer: 1
8. What is the value of 3P² -5P + 6 at P =1?
- 6
- 4
- 5
- 7
Answer: 2
9. Find the value of 6b – 3a for a = 2, b = 1.
- 3
- 4
- 0
- 7
Answer: 3
10. Choose the correct matching.
1) \(\frac{2 m}{5} \) at m = 5 ( ) a) 20
2) x² + 8x at x = 2 ( ) b) 6
3) a² + b at a = 0, b =1 ( )(c) 1
4) pq at p = 2, q = 3 ( ) d) 2
- i – d,ii – a,iii – c, iv – b
- i -b,ii – c,iii – a, iv – d
- i – b,ii – a,iii – c, iv – d
- i – a,ii – b,iii – d, iv-c
Answer: 1
11. What is the value of the expression 2x²y + xy² + xy at x = ( -1) and y = 2?
- -4
- -2
- -6
- -8
Answer: 2
12. Value of x²-y + 2 at x = 0, y = -1 is
- -3
- 2
- 3
- 1
Answer: 3
13. What is the coefficient of ‘P²’in 4P²y- 5P
- 4
- 4y
- A or B
- None
Answer: 2
14. What do we call the terms with same algebraic factors?
- unlike terms
- like terms
- constants
- variables
Answer: 2
15. a², b², c² are called
- Like terms
- Unlike terms
- Numerical terms
- None, of these
Answer: 2
16. Which of the following is a trinomial?
- 2x
- x²
- 2a-3b + c
- 2x + y
Answer: 3
17. If A = 2x- 4 then- 3A =
- -6x +12
- -4 + 2x
- 8x – 12
- 0
Answer: 1
18. If ‘n’ denotes the natural number, then formula for even number is
- n +1
- 2n +1
- 2n
- n-1
Answer: 3
19. “The cost of 5 pencils and 7 pens is 50” Expression algebraic form.
- 5x + 7y = 90
- 5x + 7y = 50
- 5y + 7x = 50
- 5y + 7x = 90
Answer: 2
20. Value of x²- 5y + 2 at x = 0, y = 3 is
- -3
- 2
- -13
- 1
Answer: 3
Haryana Board Class 7 Maths Solutions For Chapter 10 Fill in the blanks:
21…….. are formed from variables and constants
Answer: Algebraic expressions
22. Expressions are made up of……….
Answer: terms
23. A term is a ………..
Answer: product of factors
24. Terms which have the same algebraic factors are called………
Answer: like terms
25. The…..is the numerical or alphabetical factor of the term.
Answer: coefficient
26. Factors containing variables are said to be……….
Answer: algebraic factors
27. Tire value of 7x – 3 at x = 5 is…….
Answer: 32
28. The nth term of tire number pattern 6, 11,16, 21…..is………
Answer: 5n +1
29. Match the following:
1. The perimeter of the equilateral triangle whose side l is ( ) A) 4l
2. The perimeter of a square whose side l is ( ) B) 2n
3. The perimeter of a regular pentagon whose sidel is ( ) 3) 3l
4. If a natural number is denoted by n, general form of a even number is ( ) D) 2n+1
5. If a natural number is denoted by n, the general form of an odd number is ( ) E) 5l
Answer:
1. C 2. A 3. E 4. B 5. D
