Haryana Board Class 7 Maths Solutions For Chapter 4 Simple Equations
- Equation: An open sentence containing the sign of equality is called an “equation. “
- Linear equation: An equation involving one variable with highest power T, is called a “Linear equation” or ‘Simple equation’.
- Solution: The value which when substituted for the variable in an equation makes LHS = RHS is called ti “solution” or “root of the given equation”.
- Properties of equality:
- Reflexive property: Every number is equal to itself.
Eg: 6 = 6, x = x etc. - Symmetric property: If a, b are two numbers and a = b, then b = a
Eg: (6 + 3) = (8 + 1) hence (8+1) = (6+3) - Transitive property: Ifa = b and b = c then a = c for any three numbers a, b, c.
Eg: 10 + 5 = 15, 15 = 3×5
∴ 10 + 5 = 3 x 5
If x = a and x = b, then a = b, for any three numbers x, a, b.
Eg: 12 = 8 + 4, 12 = 7 + 5 .-.8 + 4 = 7 + 5 - Addition Property: If a = b, then a + c = b + c where a, b, c are any three numbers.
- Subtraction Property: If a = b, then a-c =b-c where a, b, c are any three numbers.
- Multiplicative Property: Ifa = b, then ab = be, where a, b, c are any three numbers.
- Division Property:Ifa = b, then = \( \frac{a}{c}=\frac{b}{c} \) where a,b,c are any three numbers and c=0.
- Reflexive property: Every number is equal to itself.
- We can add the same number to both sides ofan equation.
- We can subtract the same number from both sides of an equation.
- We can multiply both sides of an equation by the same non-zero number.
- We can divide both sides of an equation by the same non-zero number.
- In transforming terms from L.H.S. to R.H.S.
‘+ quantity’ becomes ‘- quantity’
‘- quantity’ becomes ‘+ quantity’
‘x quantity’ becomes ‘÷quantity’
‘÷ quantity’ becomes ‘x quantity’ - Transposition: We can drop any term from one side of an equation and take it to the otherside with its sign changed. This process is called “Transposition”.
- Simple equation: An equation in one variable with highest power 1 is known as Simple equation.
Eg: y – 7 = 11; 2m- 5 = m + 7 - Bhaskara – II: Bhaskara-II is a famous mathematician of an ancient India. He wrote ‘Siddhanta Shiromani’.
- Variables: The word variable means something that can vary i e. change. A vanable takes on different numerical values; its value is not fined Variables ore denoted usually by letters of the alphabets such as x, y, z, l, m, n, p. etc.
- Expressions: Expressions ore formed by performing operations like addition, subtraction, multiplication and division on the variables.
Example: 4x + 5 - Equations: An equation is a kind of condition on a vanable. An expression equated to some value is called an equation.
Example: 4i + 5 – 9 - Value of an expression:
The value of an expression depends upon the value of the variable from which the expression is formed.
Example: 4x + 5
At x-0; 4×0+ 5= 0 + 5=5
At x=l; 4×1+ 5=4 + 5=9
At x=2; 4×2+ 5=8 + 5=13
At x=5; 4×5+ 5=20 + 5=25
Haryana Board Class 7 Maths Solutions For Chapter 4 Exercise – 4.1 :
1. Complete the last column of the table
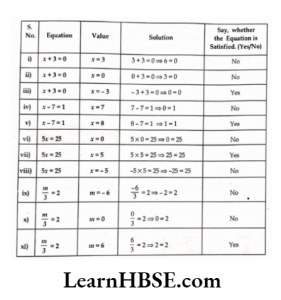
Haryana Board Class 7 Maths Simple Equations solutions
2. Check whether the value given in the brackets is a solution to the given equation or not:
1) n + 5 = 19 (n = 1)
Solution: 11 + 5 = 19
n =1;
LHS =1+5=6
RHS =19
LHS ≠ RHS
n =1 is not a solution.
HBSE Class 7 Simple Equations Solutions
2) 7n + 5 = 19 (n = -2)
Solution: 7H + 5 = 19
n= -2;
LHS = 7n + 5
= 7 (-2) + 5 = -14 + 5 = -9
RHS = 19
LHS ≠ RHS
n = – 2 is not a solution.
3) 7n + 5 =19 (n=2)
Solution: 7n + 5 = 19
n = 2
LHS = 7n + 5
= 7 x 2 + 5 = 14 + 5-19
RHS = 19
LHS = RHS
n = 2 is a solution
How to solve linear equations Class 7 HBSE
4) 4p – 3 = 13 (p = 1)
Solution:
4p-3 = 13
p-1 ;
LHS = 4p -3
=4 x 1- 3 = 4 – 3 = 1
RHS = 13
LHS ≠ RHS
p =1 is not a solution.
5) 4p – 3 = 13 (p = – 4)
Solution:
4p – 3=13
p = -4;
LHS = 4p – 3
4(- 4) – 3 = – 16 – 3 = -19
RHS = 13
LHS ≠ RHS
p = – 4 is not a solution.
6) 4p-3 = 13 (p = 0)
Solution:
4p – 3 = 13
p = 0;
LHS =4p-3
= 4(0) – 3 = 0- 3 = -3
RHS = 13
LHS ≠ RHS
p = 0 is not a solution
3. Solve the following equations by trial and error method:
1) 5p + 2 = 17

p = 3 is the solution.
2) 3m- 14 = 4

Solution:
m= 6 is the solution.
Key Questions in Simple Equations for Class 7 HBSE
4. Write equations for the following statements:
1) The sum of numbers x and 4 is 9.
Solution: 1 + 4-9
2) 2 subtracted from y is 8.
Solution: y- 2 = 8
3) Ten times a is 70.
Solution: 10a = 70
Transposition method in algebra Class 7 Haryana Board
4) The number h divided by 5 gives 6.
Solution: \( \frac{b}{5} \)
5) Three-fourth of t is 15
Solution: \( \frac{3}{4} t=15 \)
6) Seven times m plus 7 gets you 77.
Solution: 7m + 7 = 77
7) One – fourth of a number ‘x’ minus 4 gives 4.
Solution: \( \frac{1}{4} x-4=4 \)
8) If you take away 6 from 6 times y, you get 60.
Solution: 6y- 6 60
9) If you add 3 to one – third of z, you get 30.
Solution: \( \frac{1}{3} z+3=30 \)
5. Write the following equations in statement forms :
1) p + 4 = 15
Solution: Sum of p and 4 is 15.
2) m – 7- 3
Solution: The difference between m and 7 is 3.
3) 2m = 7
Solution: Two times m is 7
4) \( \frac{m}{5}=3 \)
Solution: One-fifth of m is 3
5. \( \frac{3 m}{5}=6 \)
Solution: Three-fifth of m is 6.
6) 3p + 4 = 25
Solution:
If we add 4 to three times of p we get 25.
Sample Problems Simple Equations Haryana Board Class 7
7) 4p – 2 =18
Solution: 2 subtracted from four times of p gives 18
8) \( \frac{p}{2}+2=8 \)
Solution: Adding 2 to half of p gives 8
Haryana Board Class 7 Maths Solutions For Chapter 4
1) Irfan says that he has 7 marbles more than five times the marbles Parmit has. Irfan has 37 marbles. (Take m to be the number of Parmit’s marbles.)
Solution:
Let Parmit have ’m’ marbles
Five times of m is 5m
7 more than five times of m – 5m + 7
i.e. Irfan has 5m + 7 marbles.
But it is given that Irfan has 37 marbles
5m + 7 = 37 is the requirrd equation.
2) Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age. (Take Laxmi’s age to be ‘y’ years.)
Solution:
Let the age of Laxmi be ‘y’ years
Three times Laxmi’s age = 3y yearss
Laxmi’s father is 4 years older than three times Laxmi’s age.
Age of Lnxmi’s father = 3y + 4 years.
It is given that Laxmi’s father is 40 years old.
3y + 4 = 49 is the required equation.
Solving simple equations step by step Class 7 HBSE
3) The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus 7. The highest score is 87. (Take the lowest score to be T.)
Solution:
Let the lowest score be l.
Twice the lowest marks = 2l.
Highest score obtained by a student in her class is twice the lowestmarks plus 7.
i.e., Highest score =2l+ 7
Given that the highest score is 87.
2l+ 7 = 87 is the required equation.
4) In an isosceles triangle, the vertex angle is twice either base angle. (Let the base angle be ‘b’in degrees. Remember that the sum of angles of a triangle is 180 degrees.)
Solution:
Let the base angle be ‘b’ degrees
Vertical angle = Twice the base angle = 2b degrees
Sum of the angles of triangle = 180° b + b + 2b = 180°
4b = 180° or b = 45° is the required equation.
Haryana Board Class 7 Maths Solutions For Chapter 4
1) When you multiply anumber by 6 and subtract 5 from the product you get 7. Can you tell what the number is?
Solution:
Let the number be x
Multiplying by 6it becomes 6x
Subtract 5 from the product it becomes 6x-5
Given its value is 7
6x- 5 = 7
Transposing- 5 from LHS to RHS
6x = 7 + 5
6x = 12
(or)
\( x=\frac{12}{6}=2 \)The required numberis 2.
2) What is that number one-thirdofwhich added to 5 gives 8?
Solution:
Let the number be x
One – third of that number is \( \frac{1}{3} \times x=\frac{x}{3} \)
Add 5 to it
\( \frac{x}{3}+5 \)Given its value is 8
\( \frac{x}{3}+5=8 \)Transposing 5 from LHS to RHS
\( \begin{aligned}\frac{x}{3} & =8-5 \\
& \Rightarrow \frac{x}{3}=3
\end{aligned} \)
Multiplying both sides by 3 we get
\( \frac{x}{3} \times 3=3 \times 3 \text { or } \mathrm{x}=9 \)The required number is 9.
Haryana Board Class 7 Maths Solutions For Chapter 4
1. There are two types of boxes containing mangoes. Each box of the larger type contains 4 more mangoes than the number of mangoes contained in 8 boxes of the smaller type. Each larger box contains 100 mangoes. Find the number of mangoes contained in the smaller box.
Solution:
Let the number of mangoesin the small box be x.
Number of mangoesin larger type box are 4 more than the number of mangoes contained in 8 boxes of the smaller type.
Equation is 8x + 4 = 100
Transposing 4 froms LHS to RHS
8x = 100 – 4
8x = 96
Dividing both sides by 8 we get
\( \frac{8 x}{8}=\frac{96}{8} \Rightarrow 64 x=768 \) \( x=\frac{768}{64} \)x= 12
The number of mangoes contained in the smaller box are 12
Solving Equations Class 7 Haryana Board
Haryana Board Class 7 Maths Solutions For Chapter 4 Exercise-4.3
1. Setup equations and solve them to find the unknown numbers in the following cases:
(1) Add 4 to eight times a number; you get 60.
Solution: Let the number be x
Eight times the number is 8x
Add 4 to this product it becomes 8x + 4
Given its value is 60
8x + 4 = 60
Transposing 4 from LHS to RHS
8x = 60- 4
=> 8x = 56
Dividing both sides by 8 we get
\( \begin{aligned}& \frac{8 x}{8}=\frac{56}{8} \Rightarrow 64 x=448 \\
& x=\frac{448}{64}
\end{aligned} \)
⇒ x = 7
The required number is 7.
2) One-fifth of a number minus 4 gives 3.
Solution:
Let the number be x
One -fifth of this number is \( x \times \frac{1}{5}=\frac{x}{5} \)
Subtracting 4 from it we get
\( \frac{x}{5}-4 \)Given its value is 3
\( \frac{x}{5}-4=3 \)Transposing – 4 from LHS to RHS
\( \begin{aligned}& \frac{x}{5}=3+4 \\
& \Rightarrow \frac{x}{5}=7
\end{aligned} \)
Multiplying both sides by 5 we get
\( \frac{x}{5} \times 5=7 \times 5 \)=> x = 35
The required number is 35.
3) If I take three-fourths of a number and add 3 to it,I get 21.
Solution:
Let the number be x
Three-fourth of this number is
\( x \times \frac{3}{4}=\frac{3 x}{4} \)Adding 3 to this value we get
\( \frac{3 x}{4}+3 \)Given its value is 21
\( \frac{3 x}{4}+3=21 \)Transposing 3 from LHS to RHS
\( \begin{aligned}& \frac{3 x}{4}=21-3 \\
& \Rightarrow \frac{3 x}{4}=18
\end{aligned} \)
Multiplying both sides by 4 we get
\( \begin{aligned}& \frac{3 x}{4} \times 4=18 \times 4 \\
& \Rightarrow 3 x=72
\end{aligned} \)
Dividing both sides by 3 we get
\( \begin{aligned}& \frac{3 x}{4}=\frac{72}{3} \Rightarrow 9 x=216 \\
& \Rightarrow x=24
\end{aligned} \)
=> x = 24
The required number is 24.
4) When I subtracted 11 from twice a number, the result was 15.
Solution:
Let the number be x
Twice of that number is 2x
Subtracting 11 from this product, we get 2x-11
Given its value is 15
2x-11 = 15
Transposing – 11 from LHS to RHS
2x = 15 + 11
=> 2x = 26
Dividing both sides by 2 we get
\( \begin{aligned}& \frac{2 x}{2}=\frac{26}{2} \Rightarrow 4 x=52 \\
& x=\frac{52}{4}
\end{aligned} \)
=>x= 13
The required number is 13
5) Munna subtracts thrice the number of notebooks he has from 50, he finds the result to be 8.
Solution:
Let the number be x
Thrice of the number is 3x
On subtracting thrice the number of notebooks from 50, it becomes 50 – 3x
The result is 8
50 -3x = 8
On transposing 50 from LHS to RHS
– 3x = 8 – 50
– 3x =- 42
Dividing both sides by -3 we get
\( \begin{aligned}& \frac{-3 x}{-3}=\frac{-42}{-3} \Rightarrow 9 x=126 \\
& \Rightarrow x=\frac{126}{9} \Rightarrow x=14
\end{aligned} \)
The required number is 14.
HBSE Class 7 Maths Chapter 4 Guide
6) Ibenhal thinks a number. If she adds 19 to it and divides the sum by 5 she will get 8.
Solution:
Let the number be x
Adding 19 to it, we get x + 19
Dividing the sum by 5 we get \( \frac{x+19}{5} \)
The result is 8
\( \frac{x+19}{5}=8 \)Multiplying both sides by 5 we get
\( \frac{x+19}{5} \times 5=8 . \times 5 \)=> x+ 19 = 40
Transposing 19 from LHS to RHS
x= 40 – 19
x= 21
The required number is 21
7) Anwar thinks of a number. If he takes away 7 from \( \frac{5}{2} \) of the number, the result is 23.
Solution:
Let the number be x
\( \frac{5}{2} \text { of the number is } \frac{5 x}{2} \)Take away 7 from it we get
\( \frac{5 x}{2}-7 \)The result is 23
\( \frac{5 x}{2}-7=23 \)Transposing -7 from LHS to RHS
\( \frac{5 x}{2}=23+7 \Rightarrow \frac{5 x}{2}=30 \)Multiplying both sides by 2 we get
\( \frac{5 x}{2} \times 2=30 \times 2 \Rightarrow 5 x=60 \)Dividing both sides by 5 we get
\( \frac{5 x}{2}=\frac{60}{5} \Rightarrow 25 x=300 \)=> x = 12
The required number is 12
2. Solve the following:
1) The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus 7. The highest score is 87. What is the lowest score?
Solution: Let the lowest score be x
Twice the lowest marks plus 7 is 87
2x + 7 = 87
Transposing 7 from LHS to RHS
2x = 87-7
=> 2x = 80
Dividing both sides by 2 we get
\( \begin{aligned}& \frac{2 x}{2}=\frac{80}{2} \Rightarrow 4 x=160 \\
& \Rightarrow x=40
\end{aligned} \)
The lowest score in the class is 40.
2) In an isosceles triangle, the base angles are equal. The vertex angle is 40°. What are the base angles of the triangle? (Remember, the sum of three angles of a triangle is 180°)
Solution:
ABC is an isosceles triangle.
The base angles are equal.
Let one of its measure be x.
Given: Vertex angle is 40°
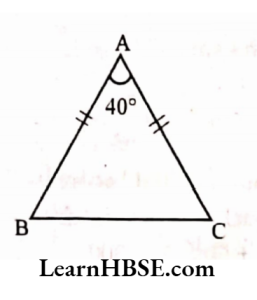
Sum of the three angles of a triangle is 180°.
i.e. ∠A+∠B+∠C = 180°
=> 40° + x + x = 180°
=> 40° + 2.V = 180°
Transposing 40° from LHS to RHS we get
2x = 180° – 40°
=> 2x = 140°
Dividing both sides by 2 we get
\( \begin{aligned}&\frac{2 x}{2}=\frac{140^{\circ}}{2} \Rightarrow 4 x=280^{\circ}\\
&\Rightarrow x=\frac{280^{\circ}}{4}
\end{aligned} \)
=> x= 70°
The base angle is 70° each
Important Concepts Simple Equations Class 7 HBSE
3) Sachin scored twice as many runs as Rahul. Together, their runs fell two short of a double century. How many runs did each one score?
Solution: Let runs scored by Rahul be x
Then runs scored by Sachin = 2x
The sum of their runs is two short of a double century.
x + 2.x + 2 = 200
=> 3x + 2 = 200
Transposing 2 froms LHS to RHS
3x = 200 -2
=> 3x = 198
Dividing both sides by 3 we get
\( \begin{aligned}& \frac{3 x}{3}=\frac{198}{3} \Rightarrow 9 x=594 \\
& \Rightarrow x=\frac{594}{9}
\end{aligned} \)
=> X = 66
Runs scored by Rahul = 66
Runs scored by Sachin = 132
3. Solve the following:
1) Irfan says that he has 7 marbles more than five times the marbles Parmithas. Irfan has 37 marbles. How many marbles does Parmit have?
Solution:
Let the number of marbles with Parmit be
If five times the number is added to 7 we get 37 marbles.
5x + 7 = 37
Transposing 7 from LHS to RHS
5x = 37-7 => 5x = 30
Dividing both sides by 5 we get
\( \begin{aligned}& \frac{5 x}{5}=\frac{30}{5} \Rightarrow 25 x=150 \\
& \Rightarrow x=\frac{150}{25} \\
& \Rightarrow x=6
\end{aligned} \)
Parmit has 6 marbles.
2) Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age. What is Laxmi’s age?
Solution:
Let Laxmi’s age be x years
Laxmi’s father is 49 years old and is 4 years older than three times Laxmi’s age.
3x + 4 = 49
Transposing 4 from LHS to RHS
3x = 49- 4
=> 3x = 45
Dividing both sides by 3 we get
\( \begin{aligned}& \frac{3 x}{3}=\frac{45}{3} \Rightarrow 9 x=135 \\
& \Rightarrow x=\frac{135}{9} \Rightarrow \mathrm{x}=15
\end{aligned} \)
Laxmi’s age is 15 years.
Word problems on simple equations Class 7 HBSE
3) People of Sundargram planted trees in the village garden. Some of the trees were fruit trees. The number of non fruit trees were two more than three times the number of fruit trees. What was the number of fruit trees planted if the number of non – fruit trees planted was 77?
Solution:
Let the number of fruit trees planted be x
Number of non – fruit trees = 3x + 2
Given non – fruit trees = 77
3x + 2 = 77
Transposing 2 from LHS to RHS
3x = 77- 2
=> 3x = 75
Dividing both sides by 3 we get
\( \begin{aligned}& \frac{3 x}{3}=\frac{75}{3} \Rightarrow 9 x=225 \\
& x=\frac{225}{9}
\end{aligned} \)
x = 25
The number of fruit trees planted are 25.
4. Solve the following riddle:
I am a number,
Tell my identity!
Take me seven times over
And add a fifty !
To reach a triple century
You still need forty !
Solution:
Let the number be x
Seven times of this number is 7 x x = 7x
On adding 50 it becomes 7x + 50
To reach a triple century we need forty
7x + 50 + 40 = 300
=> 7x + 90- 300
Transposing 90 bom LHS to RHS
7x-300-90
=> 7x- 210
Dividing both sides by 7 we get
\( \begin{aligned}& \frac{7 x}{7}=\frac{210}{7} \Rightarrow 49 x=1470 \\
& x=\frac{1470}{49} \Rightarrow x=30
\end{aligned} \)
The required number is 30.
Haryana Board Class 7 Maths Chapter 4 Very Short Answer Questions
1. What is meant by simple equation?
Solution: An equation is a condition on a variable such that two expressionsin the variable should have equal value.
2. What is meant by solution of an equation ?
Solution:
The value of the variable for which the equation is satisfied is called the solution of the equation.
3. Find the value of the expression 4x + 5 at x = 1, 2, 3
Solution:
Given expression is 4x + 5
At x =1 its value is4(l) + 5- 4 + 5- 9
x = 2 its value is 4 (2) + 5 – 8 + 5 – 13
x- 3 its value is 4 (3) + 5 = 12 + 5-17
4. “If you subtract 5 from 6 times a number you get 7” write this statement in the form of an equation.
Solution:
Let the number be x; x multiplied by 6 is 6x. Subtracting 5 from 6x, we get 6x-5.
The obtained result is 7.
6x – 5- 7
5. Solve 4 (m + 3) – 18
Solution:
4(m + 3)-18
Divide both sides by 4
m + 3 = \( \frac{18}{4} \)
=> m + 3 = \( \frac{9}{2} \)
m = \( \frac{9}{2} \) – 3
\( m=\frac{9}{2}-\frac{6}{2}=\frac{3}{2} \)Practice Problems Simple Equations Class 7 Haryana Board
6. The sum of three times a number and 11 is 32. Find the number.
Solution:
Let the number be x
3x + 11 = 32
3x = 32 – 11
3x- 21
x = \( \frac{21}{3} \) = 7
The required number is 7.
7. The sum of twice a number and 4 is 80, find the number.
Solution:
Let the number be ‘x’
Twice a number = 2x
The sum of twice a number and 4 is 80
=> 2x + 4 = 80
=> 2x = 80 – 4
=> 2x – 76
x= \( \frac{76}{2} \)
=> x = 38
The number = 38
8. Find the value of x from the adjacent diagram.
Solution: From the figure

12 + x + 5 – 24
17 + x – 24
x – 24 – 17
x – 7 cm
9. To convert temperature from Fahrenheit to Centigrade, we use the formula (F-32) = \( \frac{9}{5} \) x C.If C = -40° C then find F.
Solution:
F-32 = \( \frac{9}{5} \) x C
If C = – 40°C then F – 32 = \( \frac{9}{5} \) x -40
F – 32 = 9 x 8
F – 32 = -72
F = -72+32
F = -40°
10. Write the equations of the following mathematical statements.
1) A number A decreased by 5 is 14.
Solution: A – 5 = 14
2) Eight times of y plus 3 is -5.
Solution: Eight times of
y = 8 X y = 8y
Eight times of y plus 3 is – 5
8y + 3 = -5
3) If you add one fourth of z to 3 you get 7.
Solution:
One fourth of z = \( \frac{z}{4} \)
If we add one fourth of z to \( 3=\frac{z}{4}+3 \)
\( \frac{z}{4}+3=7 \)4) If you take away 5 from 3 times of m, you get 11.
Solution:
3 times of m = 3 x m = 3m
If we take away 5 from 3 times of m
= 3m – 5
3m- 5 = 11
5) Sum of angles 2x (x – 30) is a right angle.
Solution: The sum of angles 2x (x – 30)
= 2x + x – 30
= 3x – 30
Right angle = 90°
3x -30 = 90″
3x = 120°
6) The perimeter of a square of side ‘a’ is 14 m
Solution:
The side of a square is ‘a’ m
Perimeter of a square = 4 x side
= 4 x a = 4a m.
The result is => 4a = 14 m.
11. Write the following equations in statement form.
1) m – 5 =12
Solution: ‘m’ is decreased by 5 is 12.
2) \( \frac{a}{3}=4 \)
Solution: One third of number ‘a’ is 4.
3) 4x + 7 = 15
Solution: 4 times of ‘x’ and 7 is 15
4) 2 – 3y = 11
Solution: 2 is decreased bv 3 time ‘y’ is 11
12. Write any three equivalent equations having the solution a = -5
Solution:

Here a + 7 = 2; a-10 = -15 and 3a + 5 = -10 are equivalent equations because they have the same solution a = – 5
13. The difference between two numbers is 7. Six times the smallerplus the larger is 77. Find the numbers.
Solution:
Let the smaller number be ‘x’
The differencebetween two numbers =7
Larger number = x +7
Six times of smaller plus the largeris 77
=> 6x + x + 7 = 77
=> 7x +7 = 77
=> 7x = 77 -7
=> 7x = 70
\( \frac{70}{7} \)=>x = 10
The smaller number = 10
Larger number = x + 7
= 10 + 7 = 17
14. In a class of 48 students, the number of girls is one third the number of boys. Find the number of girls and boys in the class.
Solution:
Let the number of boys be ‘x
then number of girls = \( \frac{x}{3} \)
Total students in the class is 48
\( \begin{aligned}& \Rightarrow \quad x+\frac{x}{3}=48 \\
& \Rightarrow \quad \frac{3 x+x}{3}=48 \\
& \Rightarrow \quad \frac{4 x}{3}=48 \\
& \Rightarrow 4 x=48 \times 3 \\
& \Rightarrow 4 x=144 \\
& \Rightarrow x=\frac{144}{4} \\
& \Rightarrow x=36
\end{aligned} \)
Number of boys = 36
\( \begin{aligned}\text { Number of girls } & =\frac{x}{3}=\frac{36}{3} \\
& =12
\end{aligned} \)
15. A sum of 500 is in the form of notes of denominations of 5 and 10. If the total number of notes is 90 then find the number of notes of each type.
Solution:
Total number of notes
Let the 5 notes be x then the 10 notes = 90 -x
5 denomination amount = 5x
10 denomination amount = 10 (90-x)
= 900 – 10x
Total amount = 500
=> 5x + 900 – 10 x =500
=> 900 – 5x = 500
=>-5x = 500-900
=>-5x = -400
=> 5x= 400
=> \( x=\frac{400}{5} \)
=> x = 80
Number of notes of 5 = 80
Number of notes of 10 = 90 – x
= 90 – 80 = 10
16. Suhana said, “multiplying my number by 5 and adding 8 to it gives the same answer as subtracting my number from 20. Find Suhana’s number.
Solution:
Let Suhana’s number be ‘x’
From the problem, we have
5x x + 8 = 20-x
5x + 8 = 20 – x
By transposing variables and constants,
5x + x = 20- 8
6x= 12
\( x=\frac{12}{6} \)[Transposing 6 to R.H.S]
Suhana’s number is 2
Haryana Board Class 7 Maths Chapter 4 Long Answer Questions
17. Check whether the value given in the brackets is a solution to the given equation or not.
1) 5n – 7 = 23 (n = 6)
Solution:
When n = 6
LHS = 5n -7
= 5(6) – 7 = 30- 7
= 23
RHS = 23
LHS = RHS
So n = 6 is a solution.
2) \( \frac{p}{4}-7 \) = 5 (p = 8)
Solution: When p = 8
LHS = \( \frac{p}{4}-7 \) = \( \frac{8}{4} \) -7
= 2- 7 = -5
RHS = 5
LHS = RHS
So ‘p’ = 8 is not a solution
3) 5 – 2x = 19 (x = -7)
Solution: When x = -7
LHS = 5 – 2x = 5 – 2(-7)
= 5 + 14 = 19
RHS = 19
LHS = RHS
So, x = -7 is a solution
4) 2 + 3 (m – 1) = 5 (m = -2)
Solution:
When m = -2
LHS = 2 + 3 (m – 1)
= 2 + 3 (-2- 1) = 2 + 3(-3)
= 2-9 = -7
RHS = 5
LHS = RHS
m = -2
So, ‘m’ = -2 is not a solution
