Haryana Board Class 7 Maths Solutions For Chapter 5 Lines and Angles

Haryana Board Class 7 Maths Solutions For Chapter 5 Lines and Angles

Key Concepts

1. Line segment:

A line segment has two end points.

A line segment.PQ is generally denoted by PQ.

2. Line (or) Straight line:

If the end points of a line segment are extended in either direction endlessly, we get a line or a straight line.

A line AB is denoted by AB

3. Ray:

A line which has only one end point is called a ray.

OP is a ray.It is denoted by OP.

Haryana Board Class 7 Maths Lines and Angles solutions

4. Examples of line segments in our daily life:

1. An edge of a box
2. A tube light
3. An edge.of a post card

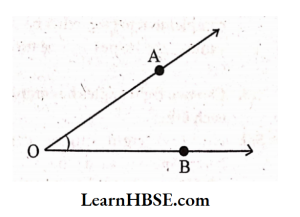
Angle:

An angle is formed when lines or line segments meet at a common point. This common point is called vertex of angle and the line segments are called its, arms or sides.

The common point ‘O’ is the vertex.

Lines OA, OB are arms of the given angle AOB. Angle AOB is denoted by ∠AOB.

Types of Angles:

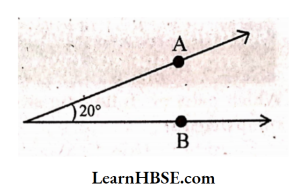
Acute angle:

An angle which is greater than 0° but less than’90° is called an acute angle.

Example: 15°, 20°, 30°, 35°, 50°, 65°, 75°, 80°, 85°

HBSE Class 7 Lines and Angles Solutions

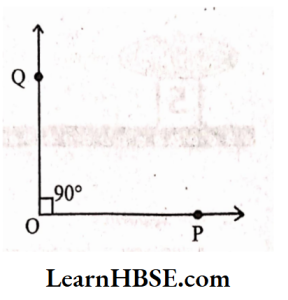
Right angle:

An angle whose measure is. 90° is called a right angle.

Types of angles and their properties Class 7 HBSE

Obtuse angle:

An angle which is greater than 90° but less than 180° is called an obtuse angle.

Example: 95°, 110°, 120°, 150°, 165°, 175° etc. are all obtuse angles.

Haryana Board Class 7 Maths Solutions For Chapter 5 Solutions

1. List ten figures around you and identify 170° the acute, obtuse and right angles found in them.

Solution:

Students can do this with the help of their teacher.

1. Can two acute angles be complement to each other?

Solution: Yes, two acute angles can be complement to each other only if their sumis equal to90°.

2. Can two obtuse angles be complement to each other?

Solution:

No, two obtuse angles cannot be complement to each other because their sum of the angles will be greater than 90°.

3. Can two right angles be complement to each other?

Solution:

No, two right angles cannot be complement to each other.

Key Questions in Lines and Angles for Class 7 HBSE

1. Which pairs of following angles are complementary?

1)

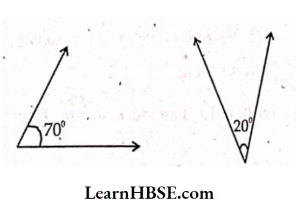
Solution:

70° + 20° = 90°

These angles are complementary

2)

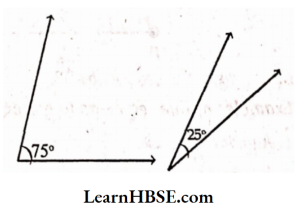
Solution:

75° + 25° = 100°

These angles are not complementary

3)

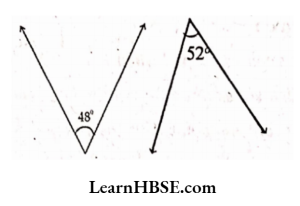
Solution:

48° + 52° = 100°

90°. These angles are not complementary.

4)

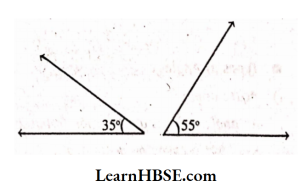
Solution:

35° + 55° = 90°

These angles are complementary.

Parallel lines and transversal angles Class 7 HBSE

1 What is the measure of the complement of each of the following angles ?

1) 45°

Solution:

Complement of the angle 45° is 90°- 45°= 45°

2) 65°

Solution:

Complement of the angle 65° is 90°- 65° = 25°

3) 41°

Solution:

Complement of the angle 41° is 90°- 41°= 49°

4) 54°

Solution:

Complement of the angle 54° is 90°- 54° = 36°

Practice Problems Lines and Angles Class 7 Haryana Board

3. The difference inanglesthe measuresis 12°. Find of two the measures of the angles

Solution:

Let the angle be x°

Its complement is 90″ – xc

Their difference * 12°

x°- (90°- x) =12°

x° – 90° + x° = 12°

2x° =12°+ 90°

2x° – 102°

\( \text { or } x^{\circ}=\frac{102}{2}=51^{\circ} \)

First angle = 51°

Second angle = 90° – 51° =39°

The required angles are 51°, 39°.

1. Can two obtuse angles be supplementary?

Solution:

So, two obtuse angles cannot be supplementary’ because the sum of two obtuse angles would be more than 180°:

2. Can two acute angles be supplementary?

Solution: No, two acute angles carrot be supplementary because their sum would be less than 180°.

3. Can two right angles be supplementary?

Solution:

Yes, two right angles can be supplementary. Because measure of each right angle is 90°.

90° + 90°= 180°= Supplementary

1. Find the pair of supplementary angles:

1). 

Solution:

Sum of these angles = 110°+ 50° = 160°

These are not supplementary angles

2) 

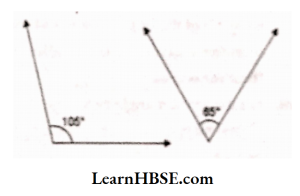
Solution:

Sum of these angles = 105° + 65 ° = 170°

These are not supplementary angles.

3)

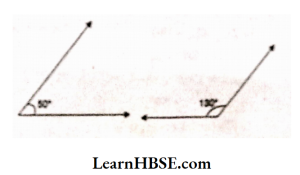
Solution:

Sum of these angles = 50° + 130° = 180°

These are supplementary angles

4)

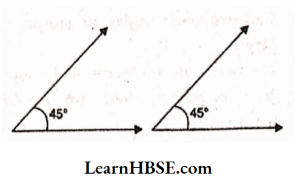
Solution:

Sum of these angles = 45° + 45° = 90°

These are not supplementary angles

HBSE 7th Class Complementary and Supplementary Angles

2. What will be the measure of the supplement of each one of the following angles?

1) 100°

Solution:

We know that the sum of two supplementary angles is 180°.

Supplement of 100° is 180° – 100° = 80°

2) 90°

Solution:

Supplement of 90° is 180° – 90° = 90°

3) 55°

Solution:

Supplement of 55° is 180° – 55° = 125°

4) 125°

Solution: Supplement of 125° is 180° – 25° = 55°

Important questions for Lines and Angles Class 7 HBSE

3. Among two supplementary angles the measure of the larger angle is 44° more than the measure of the smaller. Find their measures.

Solution:

Let the smaller angle be x.

Its supplement bigger angle is (x + 44)°

We know that the sum of two supplementary angles is 180°.

x + (x + 44)° =180°.

=> 2x + 44° = 180°

=> 2x = 180° – 44°

=>2x = 136°

\( x=\frac{136^{\circ}}{2}=68^{\circ} \)

The smaller angle is ’68°.

Its supplement larger angle is 68° + 44° = 112°

Exercise-5.1

1. Find the complement of each of the following angles:

Solution:

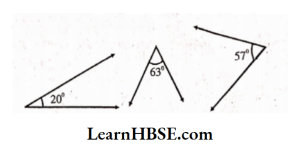
Sum of two complementary angles is 90°.

1) Complement of the angle 20° is 90°-20° =70°

2) Complement of the angle 63° is 90°-63°= 27°

3) Complement of the angle 57° is 90°-57° =33°

2. Find the supplement of each of the following angles:

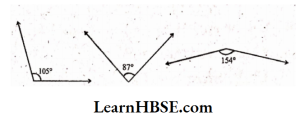
Solution:

Sum of two supplementary angles is 180°.

1) Supplement of the angle 105° is 180°- 105° = 75°

2) Supplement of the angle 87° is 180°-87° = 93°

3) Supplement of the angle 154° is 180°- 154° = 26°

Sample Problems Lines and Angles Haryana Board Class 7

3. Identify which of the following pairs of angles are complementary and which are supplementary.

1) 65°, 115°

Solution:

Sum of the angles = 65° + 115°= 180°.

The given angles are supplementary

2) 63°, 27°

Solution:

Sum of the angles = 63° + 27° = 90°

The given angles are complementary.

3) 112°, 68°

Solution: Sum of the angles = 112° + 68° = 180°

The given angles are supplementary.

4) 130°, 50°

Solution: Sum of the angles = 130° + 50° = 180°

The given angles are supplementary.

5) 45°, 45°

Solution: Sum of the angles =45° + 45° = 90°

The given angles are complementary.

6) 80°, 10°

Solution: Sum of the angles = 80°+ 10° = 90°

The given angles are complementary.

4. Find the angle which is equal to its complement.

Solution:

Let the angle be x°

Its complementis 90°- x°

Given that the angle is equal to its complement.

i.e. x° = 90°- x°

=> x° + x° = 90°

=> 2x° = 90°

\(\Rightarrow x^{\circ}=\frac{90^{\circ}}{2} \Rightarrow x=45^{\circ} \)

The required angle is 45°

5. Find the angle which is equal to its supplement.

Solution:

Let the angle be x°

Its supplement is 180°- x°

Given that the angle is equal to its supplement.

i.e. x° = 180°- x°

x° + x° = 180°

2x°=180°

\( x=\frac{180^{\circ}}{2} \)

x° = 90°

The required angle is 90°

6. In the given figure, ∠1 and ∠2 are supplementary angles. If ∠1 is decreased, what changes should take place in ∠2 so that both the angles still remain Supplementary.

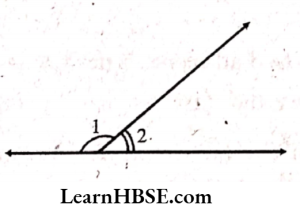
Solution:

If A is decreased then ∠1 should be increased so that both the angles still remain supplementary.

7. Can two angles be supplementary if both of them are:

1) acute? (2) obtuse? (3) Right?

Solution:

Two angles are supplementary if their sum is 180°.

1) No;if two angles are acute (0° < x < 90°) then their sum cannot be equal to 180°.

2) No;iftwo angles are obtuse (90°<x<180°) then their sum cannot be equal to 180°.

3) Yes; if two angles are at right angles (= 90°) then their sum is equal to 180°.

Types of Angles Class 7 Haryana Board

8. An angle is greater than 45°. Is its complementary angle greater than 45° or equal to 45° or less than 45°.

Solution:

The sum of two complementary angles is 90°. Its complementary angle is less than 45°.

9. Fill in the blanks:

1) If two angles are complementary, then the sum of their measures is…………… (90°)

2)  If two angles are supplementary, then the sum of their measures is…………….. (180°)

3) If two adjacent angles are supplementary, they form a…….. (linear pair)

10. In the adjoining figure, name the following pairs of angles.

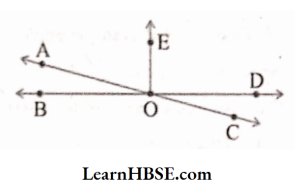
1) Obtuse vertically opposite angles.

Solution: ∠AOD and ∠BOC

2) Adjacent complementary angles.

Solution: ∠AOB and ∠AOE

3) Equal supplementary angles.

Solution: ∠BOE and ∠EOD

4) Unequal supplementary angles.

Solution: ∠EOA and ∠EOC

5) Adjacent angles that do not form a linear pair

Solution:

∠AOB and ∠AOE; ∠AOE and ∠EOD; ∠EOD and ∠COD

1. Find examples from your surroundings where lines intersect at right angles.

Solution: Comers of the walls, sides of a box.

2. Find the measures of the angles made by the intersecting lines at the vertices of an equilateral triangle.

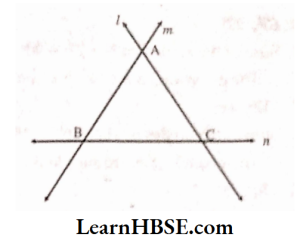
Solution:

l, m, and n are three lines forming an equilateral triangle ABC. Angles formed are A, B,C We see that each angle is 60°.

3. Draw any rectangle and find the measures of angles at the four vertices made by the intersecting lines

Solution:

PQRS is a rectangle formed by four lines k, l, m, n.

Angles at vertices P, Q, R, S are at right angles.

4. If two lines intersect, do they always intersect at right angles?

Solution:

No, they may not always intersect at right angles.

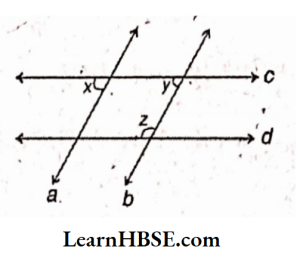
1. Suppose two lines are given. How many transversals can you draw for these lines?

Solution:

We can draw an infinite number of transversals

2. If a line is a transversal to three lines,how many points of intersections are there?

Solution: When a line is a transversal to three lines then there are three points of intersection.

3. Try to identify a few transversals in your surroundings.

Solution:

1. A road crossing two or more roads.

2. A railway line crossing several other lines.

Name the pairs of angles in each figure :

1.

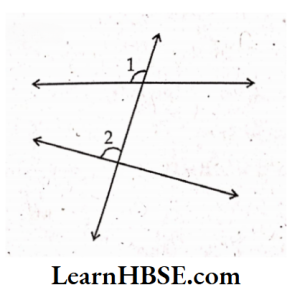
Solution: ∠1,∠2 are pair, of corresponding angles

2.

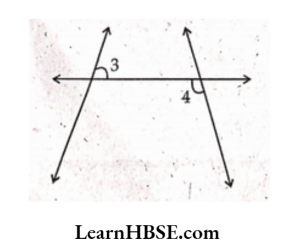
Solution: ∠3.∠4 are pair of alternate interior angles

3.

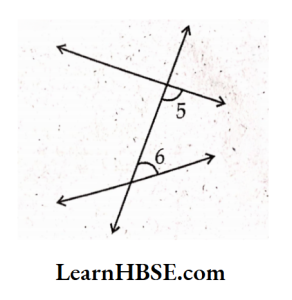
Solution: ∠5, ∠6 pair of inferior angles on the same side of the transversal

4.

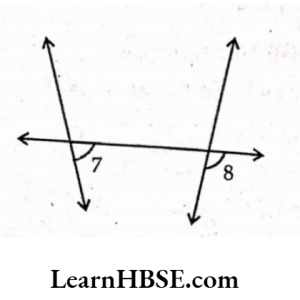
Solution: ∠7, ∠8 are pair of corresponding angles.

5.

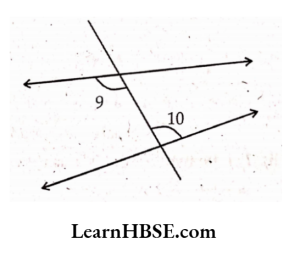
Solution: ∠9, ∠10 are pair of alternate interior 1 angles.

6.

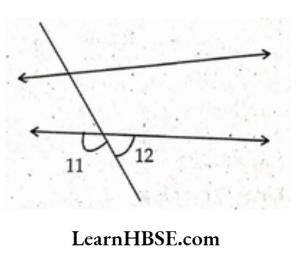
Solution: ∠11, ∠12 form a linear pair.

1) Lines l \\m; t is a transversal, x =?

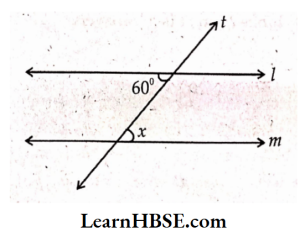
Solution:

Given: l \\m; t is a transversal.

∠x = 60° (Alternate interior angles)

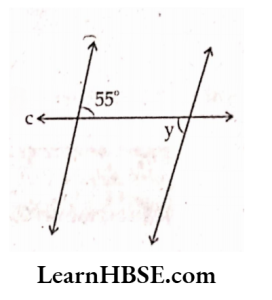
2) Lines a \\ b; c is a transversal, ∠y= ?

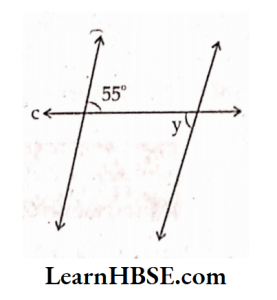
Solution:

Given: a \\ b; c is a transversal.

∠y = 55° (Alternate interior angles)

Complementary and supplementary angles Class 7

3) l1,l2 be two lines; t is a transversal. Is ∠1 = ∠2?

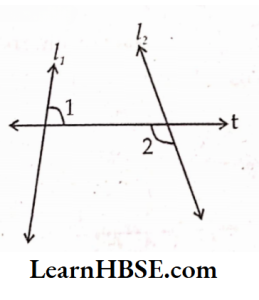
Solution:

No. ∠1 = ∠2

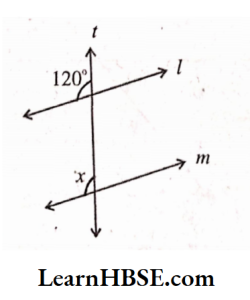
4) Lines l\\m; t is a transversal. ∠z = ?

Solution:

∠z + 60° = 180°

∠z = 180°- 60°

= 120°

5) Lines l \\m; t is a transversal, ∠x = ?

Solution:

Given: l \\ m; t is transversal.

∠x = 120° (pairs of corresponding angles)

6) Lines l\\m,p\\q; Find a, b, c, d

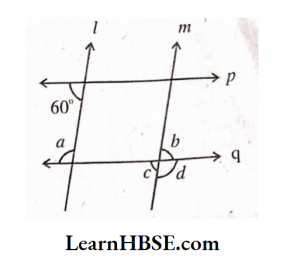
Solution:

Given: p\\q and l is transversal.

∠a + 60° = 180°

=> ∠a = 180°- 60° = 120°

l \\m and q is transversal.

∠a = ∠1 (pair of corresponding angles)

∠1 = 120°

∠d = ∠1 =120°(vertical opposite angles)

∠1 + ∠c = 180° (linear pair)

120° + ∠c = 180°

= ∠c =180°- 120°= 60°

∠b = ∠c

∠b = 60°

a = 120°; b = 60°; c = 60°; d = 120°

1) Is l \\m Why?

Solution:

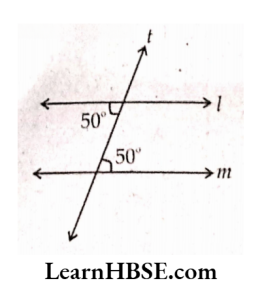
Here alternate angles are equal

l \\m

2) Is l \\m? Why?

 

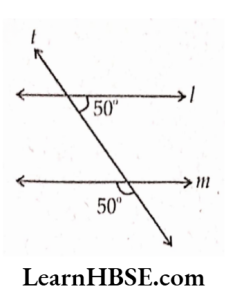
Solution: Corresponding angles are equal.

l\\m

3) If l\\m, what is ∠x ?

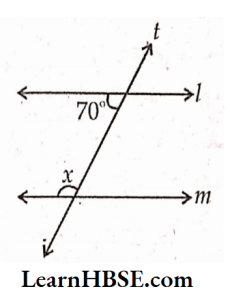
Solution:

The sum of the interior angles on the same side of the transversal are supplementary.

x + 70° = 180°

x = 180° -70°= 110°

Haryana Board Class 7 Maths Solutions For Chapter 5 Exercise 5.2 :

1. State the property that is used in each of the following statements.

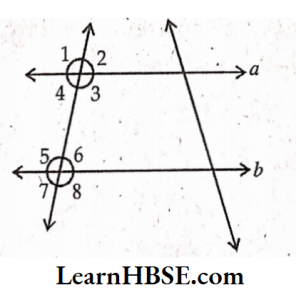
1). If a\\b, then ∠1 = ∠5.

Solution:

If a\\b, then ∠1 = ∠5

If a transversal intersects two parallel lines then the corresponding angles are equal

2) If ∠4 =∠6 then a\\b.

Solution:

∠4,∠6 are alternate interior angles.

∠4 =∠6 then a\\b.

If two parallel lines are cut by a transversal the alternate interior anglesare equal.

3) If ∠4 +∠5 = 180° then a \\ b.

Solution:

If two parallel lines are cut by a transversal then each pair ofinterior angles on the same side of the transversal are supplementary.

2. In the adjoining figure, identify

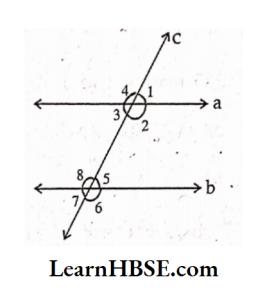
1) the pairs of corresponding angles.

Solution: ∠l, ∠5; ∠2,∠6; ∠3, ∠7; ∠4, ∠8

2) the pairs of alternate interior angles.

Solution: ∠2,∠8;∠3,∠5

3) the pairs of interior angles on the same side of the transversal.

Solution: ∠2,∠5;∠3,∠8

4) the vertically opposite angles.

Solution: ∠1,∠3;∠2,∠4;∠5,∠7;∠6,∠8

3. In the adjoining figure p \\ q. Find the unknown angles

Solution:

 

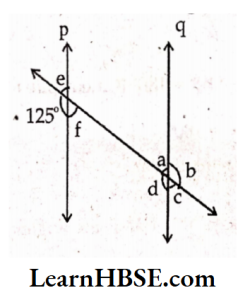
p\\q and l is transversal.

e + 125°= 180° (linear pair)

e = 180°- 125° = 55°

∠f = ∠e (vertically opposite angles)

∠f = 55°

∠a = ∠e (corresponding angles)

∠a = 55°

∠c = ∠a (vertically opposite angles)

∠c = 55°

∠d = 125°(corresponding angles)

∠b =∠d (vertically opposite angles)

∠b = 125°

a = 55°;b =125°;c= 550 d =125°;e = 55°; f = 55°

HBSE Class 7 Maths Chapter 5 Guide

4. Find the value of x in each of the following figures if l\\m.

1)

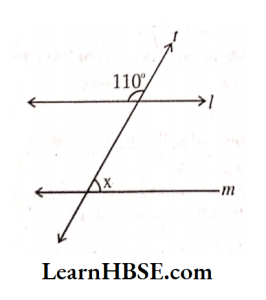
Solution: x+110° = 180° (Linear pair)

x=180°-110°

=> ∠x = 70°

∠x = 70° (alternate angles)

2)

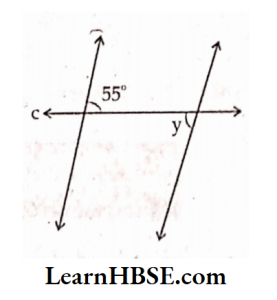
Solution: l\\m and ‘a’ is a transversal.

x = 100°( corresponding angles)

5. In the given figure the arms of two angles are parallel.

If ∠ABC= 70° then find

1) ∠DGC

2) ∠DEF

 

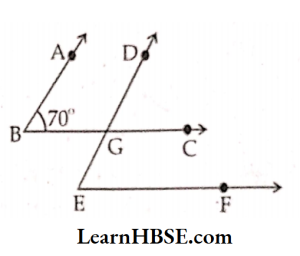
Solution:

1) AB\\DE and BC is a transversal

∠DGC=∠ABC (corresponding angles)

Given ∠ABC =70°

∠DGC = 70°

2) BC\\EF and DE is a transversal

∠DEF=DGC (corresponding angles)

∠DGC = 70°

∠DEF = 70°

6. In the given figures below, decide whether l is parallel to m

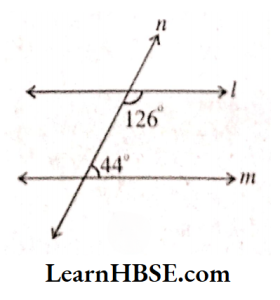
Solution:

1) l is not parallel to m Because

126° + 44°= 170° = 180°

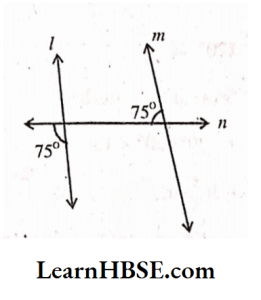
Solution: 2) l is not parallel to m

∠l =75° (vertically opposite angles)

75° + 75° = 150° = 180°

Solution:

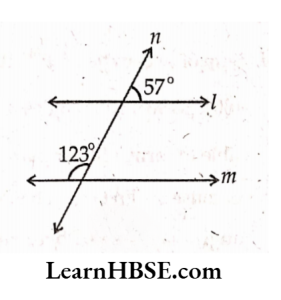
3) l is parallel to m

∠l +57° = 180°

∠l =180° -57° = 123°

Alternate angles are equal.

Solution:

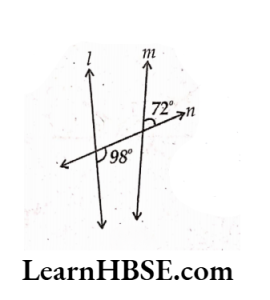
4) l is not parallel to m

∠l = ∠2 (vertically opposite angles.)

72° + 98° =170° = 180°

Haryana Board Class 7 Maths Solutions For Chapter 5 Very Short Answer Questions

1. How many end points are there for a ‘line segment’?

Solution: A line segment has two end points.

2. Define a ‘transversal’.

Solution: A line that intersect two or more lines at distinct points is called a transversal.

3. Write the angles made by a transversal.

Solution: Interior angles, exterior angles, corresponding angles, alternate interior angles, alternate exterior angles.

4. State (1) Complementary angles (2) Supplementary angles.

Solution:

(1) If the sum of the measures of two angles is 90° the angles are called complementary angles.

(2) If the sum of the measures of two angles is 180° the angles are called supplementary angles.

5. Write the properties of two parallel lines are cut by a transversal.

Solution:

1) Each pair of corresponding angles are equal in measure.

2) Each pair of alternate interior angles are equal.

3) Each pair of interior angles on the same side of the transversal are supplementary.

6. In the figure, ∠AOB and ∠COD have common vertex O. But ∠AOB, ∠COD are not adjacent angles. Why ? Give reason.

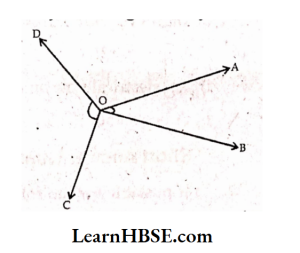
Solution:

∠AOB and ∠COD have common vertex ‘O’, but ∠AOB, ∠COD are not adjacent angles, because there is no common arm.

7. Draw a pair of adjacent angles which are supplementary to each other.

8. Write any three examples for vertically opposite angles in your surroundings.

Solution:

Examples for vertically opposite angles in our surroundings :

1. Four angles madein the scissors
2. The point where two roads intersect each other
3. Rail road crossing signs
4. Comers of the room

9. When a transversal intersects two lines and a pair of alternate exterior angles are equal, what can you say about the two lines?

Solution: ‘When a transversal intersects two lines and a pair of alternate exterior angles are equal’ “Then the two lines are parallel”.

10. Write any two examples for linear pair of angles in your surroundings.

Solution:

Examples for linear pair of angles:

1) An electrical pole on the road.

2) A pen stand. ,

Haryana Board Class 7 Maths Solutions For Chapter 5 Short Answer Questions

11. Is it possible for the following pair of angles to form a linear pair? If yes, draw them. If not, give reason

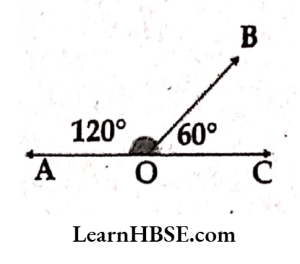
1) 120°, 60°

Solution: Sum of two angles

= 120°+60° = 180°

= linear pair

So 120° and 60° angles are possible to form a ‘linear pair1

2) 98°, 102°

Solution: Sum of two angles= 98°+102° =200°= 180°. So 98°, 102° angles are not possible to form a linear pair.

Because the linear pair has sum of two angles is 180° but here sum of two angles is 200°.

12. Name three pairs of vertically opposite angles in the figure.If ∠AOB =45°, then find ∠DOE.

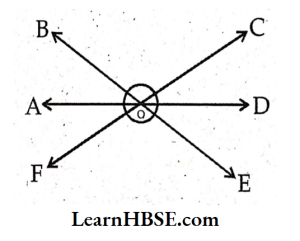
Solution: Three pairs of vertically opposite angles are:

1) ∠AOB, ∠DOE

2) ∠AOF, ∠COD

3) ∠BOC, ∠EOF

If ∠AOB = 45° then∠DOE =∠AOB = 45° (Vertically opposite angles)

∠DOE = 45°

13. In the given figure, the lines l and m intersect at point P. Observe the figure and find the values of x, y and z.

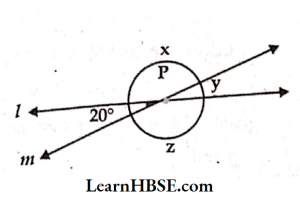
Solution: In the given figure, the linesl and m intersect at point P.

y = 20° [Vertically opposite angles]

20°+x = 180° [ Linear pair on line ‘m’]

x°= 180-20°

x° =160°

z = x° = 160° [Vertically opposite angles]

z = 160°

= 160°, y = 20°, z = 160°

14. In the figure, p\\q and t is a transversal. Observe the angles formed

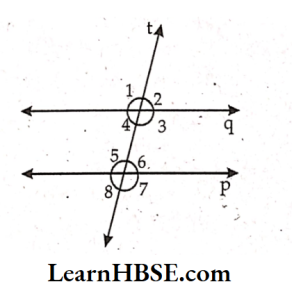
1) If ∠1 = 100°, then what is ∠5 ? 

Solution: If ∠1 = 100° then ∠5 = ∠1 = ∠100° [Corresponding angles]

2) If ∠8 = 80°, then what is ∠4?

Solution: If ∠8 = 80° then ∠4 = ∠8 = ∠80° [Corresponding angles]

3) If ∠3 = 145°, then what is ∠7?

Solution: If ∠3 = 145° then ∠7 = Z3 = ∠145° [Corresponding angles]

4) If ∠6=30°, then whatis ∠2?

Solution: If ∠6 = 30° then ∠2 = ∠6 = ∠30° [Corresponding angles]

15. From the figure, state which property that is used in each of the following.

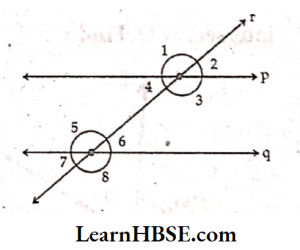
1) If ∠3 = ∠5 then p||q.

Solution: Alternate interior angle.

2) If ∠3 + ∠6 = 180° then p || q.

Solution: Co-interior angles are supplementary.

3) If ∠3 = ∠8 then p || q.

Solution: Corresponding angles

4) If p\\q then ∠1 = ∠8.

Solution: Alternate exterior angles

16. In the given figure, two lines p\\q and r is a transversal.If ∠3 =135°, then find the remaining angles

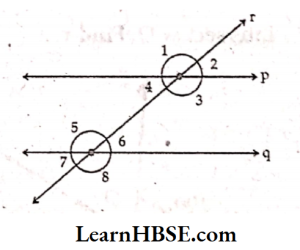
Solution:

In the given figure, p \\ q and Y is a transversal.

If ∠3 =135°, then ∠1 =∠3 = 135° ( Vertically opposite angles)

∠2+∠3 = 180°

∠2 + 135° = 180° ( Linear pair of angles)

∠2 = 180° -∠3 = 180° -135° = 45°

∠2- 45°

∠4=∠2 = 45° (Vertically opposite angles)

=> ∠5 =∠1 = 135° (Corresponding angles)

=>∠6 =∠2 = 45° (7 Corresponding angles)

=>∠7=∠4 = 45°( Corresponding angles) 80°

=>∠8 =∠3 = 135° (Corresponding angles)

∠1 =∠3 = ∠5 =∠8 =135°

∠2 = ∠4 = ∠6=∠7 = 45°

Important Concepts Lines and Angles Class 7 HBSE

17. Find the complementary, supplementary, and conjugate angle of 36°.

Solution:

The complementary angle of 36° is = 90° -36° = 54°

The supplementary angle of 36° is = 180° -36° = 144°

The conjugate angle of 36° is = 360° -36° = 324°

18. In the given figure the lines and m intersect at O. Find x

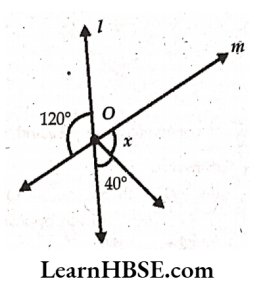
Solution:

The lines l and m intersect at ‘O’

x + 40° = 120° ( Vertically opposite angles)

=>x = 120°-40° = 80°

x = 80°

Haryana Board Class 7 Maths Solutions For Chapter 5 Long Answer Questions

19. In the given figure p, q, r, and s are parallel lines and t is a transversal. Find x, y, and z.

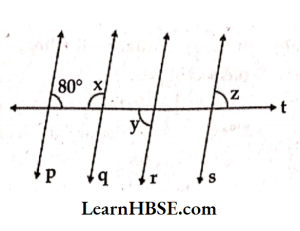
Solution: In the given figure p, q,r, and s are parallel lines, and t is a transversal.

x + 80° = 180° (Co-interior angles)

x = 180°-80°

x = 100°

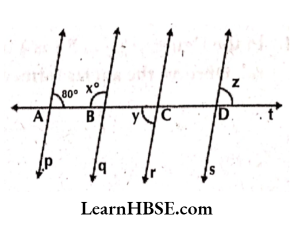
x° + ∠ABq = 180° ( Linear pair)

=>100°+ ∠ABq = 180°

=> ∠ABq = 180°- 100°= 80°

y = ∠ABq = 80° ( Corresponding angles)

y = 80°

z = y = 80°(Alternate exterior angles)

z = 80°

20. In the given figure AB \\ CD and E is a point in between them. Find x + y + z.

(Hint: Draw a parallel line to AB through E)

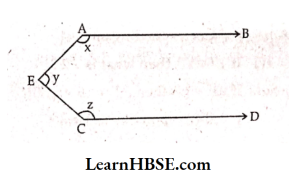
Solution: In the given figure AB \\ CD and E is a point in between them.

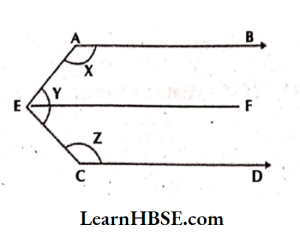
Draw a parallel line

EF to AB through E.

Consider AB \\ EF and

AE as a transversal.

∠BAE + ∠AEF = 180° ( Co-interior angles)

x° + ∠AEF = 180°

∠AEF = 180°- x -> 1

Consider CD || EF and CE as transversal.

∠DCE + ∠CEF = 180° ( Co-interior angles)

z + ∠CEF = 180°

∠CEF = 180°- z -> 2

1 + 2 =>

=> ∠AEF + ∠CEF = 180° – x + 180°- Z

∠AEC = 360° – x- z

( ∠AEC = ∠AEF + ∠CEF)

y = 360° – x- z

x + y + z =360°

Haryana Board Class 7 Maths Solutions For Chapter 5 Multiple Choice Question and Answers

Choose the correct answers:

1. A ray has …… endpoints.

1. one
2. two
3. three
4. four

Answer: 1

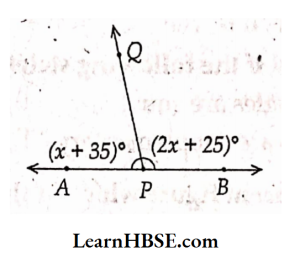
2. Find the value of x in the given figure

1. 57°
2. 58°
3. 56°
4. 55°

Answer: 1

3. Which of the following are the units of an angle?

1. meters
2. seconds
3. gnpns
4. degrees

Answer: 4

4. How many rays can we draw from a given point?

1. 1
2. 2
3. 10
4. Infinitely many

Answer: 4

5. Find the angle which is complement of itself.

1. 90°
2. 30°
3. 50°
4. 45°

Answer: 4

6. Supplementary angle of 130° =………

1. 40°
2. 60°
3. 50°
4. 90°

Answer: 3

7. One of the acute angle in right angle triangle is 30° then the other angle is

1. 30°
2. 90°
3. 70°
4. 60°

Answer: 4

8. From the adjacent figure value of x =……..

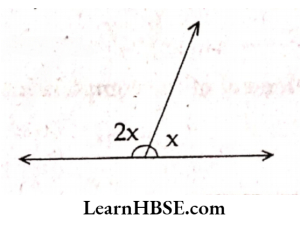
1. 60°
2. 120°
3. 90°
4. 180°

Answer: 1

9. What is x here?

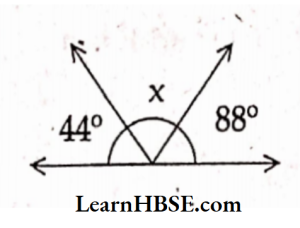
1. 28°
2. 38°
3. 48°
4. 58°

Answer: 3

10. In the figure MN || PQ. ∠MNE = 120°, ∠EPQ = 100°, what is x here ?

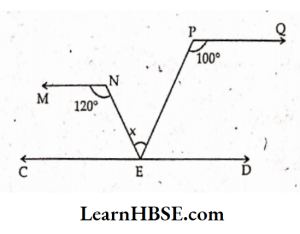
1. 20°
2. 30°
3. 60°
4. 40°

Answer: 4

11. The angle which cannot be formed by scissors

1. Acute
2. Right
3. Straight
4. Obtuse

Answer: 3

12. Angles between legs of a folding chair is an example of

1. vertically opposite angles
2. adjacent angles
3. corresponding angles
4. alternate interior angles

Answer: 1

13. In the adjacent figure J \\ BC. Find x, y.

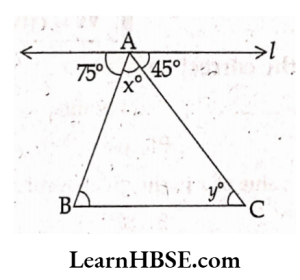
1. 60°, 45°
2. 45°, 60°
3. 75°, 45°
4. 60°, 75°

Answer: 1

14. If two lines intersect each other, then the number of common points they have

1. 1
2. 2
3. 4
4. Infinity

Answer: 1

15. The supplementary angle of 70° is

1. 20°
2. 110°
3. 290°
4. 70°

Answer: 2

16. Find the complementary angle of 55°.

1. 35°
2. 45°
3. 25°
4. 15°

Answer: 1

17. Supplementary angle of 130° is ……….

1. 130°
2. 50°
3. 70°
4. 100°

Answer: 2

18. The supplementary angle of 100° is

1. 10°
2. 40°
3. 100°
4. 80°

Answer: 4

19. The supplement of the complement of 20° is……

1. 160°
2. 70°
3. 110°
4. 90°

Answer: 3

20. The complementary angle of 57° is…….

1. 53°
2. 43°
3. 33°
4. 23°

Answer: 3

21. The supplementary angle of 55° is.

1. 105°
2. 135°
3. 125°
4. 145°

Answer: 3

22. If an angle is double of its complement then the angle is

1. 15°
2. 30°
3. 45°
4. 60°

Answer: 2

23. An angle is 30° larger than a straight angle. Then the angle is

1. 90°
2. 150°
3. 210°
4. 390°

Answer: 3

24. In the figure, the value of x is

1. 40°
2. 20°
3. 60°
4. 150°

Answer: 1

25. In the figure BOC = 60°, ∠AOC = ….

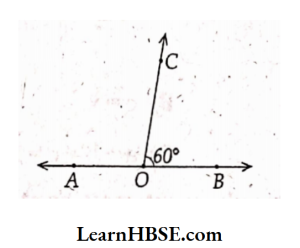
1. 90°
2. 30°
3. 120°
4. 60°

Answer: 3

26. In the figure ABCD and AECF then ∠A- ∠C = ……………

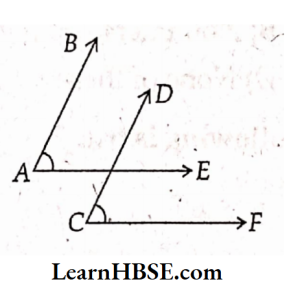
1. 0°
2. 90°
3. 45°
4. 60°

Answer: 1

27. What happens to the measurement of an angle after the extension of its arms?

1. Doubles
2. Triples
3. Remains same
4. Cannot be same

Answer: 3

28. The distance between two parallel lines is

1. unequal
2. equal
3. decreases
4. increases

Answer: 2

29. The complementary angle of an angle greater than 45°is

1. equal to 45°
2. less than 45°
3. more than 45°
4. less than 30°

Answer: 2

30. Which of the following is true?

1. Two acute angles are supplementary
2. Two obtuse angles are supplementary
3. Two right angles are supplementary
4. Two reflex angles are supplementary

Answer: 3

31. In the figure AB \\ CD and XY is the transversal. Which of the following is incorrect?

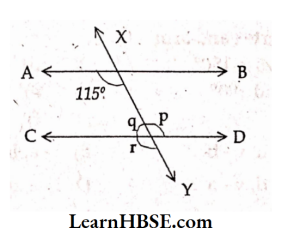
1. ∠p = 115°
2. ∠q = 115°
3. ∠q = 65°
4. ∠r = 115°

Answer: 2

32. The sum of two angles be supplementary.If both are……

1. Acute
2. Obtuse
3. Right
4. None

Answer: 2

33. I. Assertion : ∠a = ∠b
II. Reason: These are corresponding angles

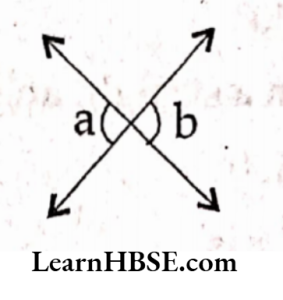
1. Statements I,II both are true
2. Statements I,II both are false
3. StatementI is true, II is false
4. StatementI is false, II is true

Answer: 3

34. Two lines are parallel if the following statements are true

1. Corresponding angles are equal
2. Co-interior angles are supplementary
3. All of the above

Answer: 4

35. According to the adjacent figure which of the following is correct where XY \\ BC?

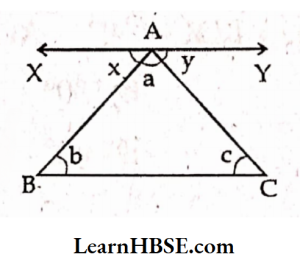
1. b = y
   
2. c = x
3.  a = b
4. a +b + c = x + a + y

Answer: 4

36. l and m are two lines intersecting at a point. These lines are called

1. Parallel lines
2. Non intersecting lines
3. None of these
4. Intersecting lines

Answer: 3

37. OA, OB are two rays. Then which of the following is true?

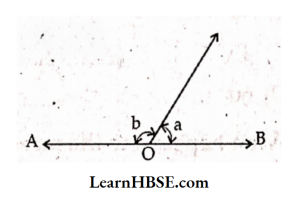
1. a + b = 90°
2. a – b = 0°
3. a + b = 180°
4. a + b = 270°

Answer: 3

38. Two lines are intersected by a transversal. The sum of the interior anglesis 130°, then the lines are

1. parallel
2. equal
3. intersect
4. none of the above

Answer: 3

39. Adjacent angles in a linear pair are

1. 80°, 20°
2. 60°, 120°
3. 45°, 90°
4. 70°, 140°

Answer: 2

40. Two complementary angles are in the ratio of 7: 2, then the angles are respectively

1. 20°, 70°
2. 70°, 20°
3. 140°, 40°
4. 35°, 10°

Answer: 2

41. Choose the correct matching.

Pair of Angles                                    Name

i) Sum of angles is 180°                       (  ) a) Linear pair

ii) Sum of angles is 90°                        (  ) b) Obtuse angle

iii) Having a common vertex and arm (  ) c) Supplementary angles

iv) Sum of adjacent angles is 180°      (  ) d) Adjacent angles

v) Angle between 90° and 180°          (  ) e) Acute angle
                                                                 f) Complementary angles

1. i – c,ii – f,iii – d, iv – a, v – b
2. i – a,ii -b,iii – d, iv – e, v – c
3. i – c,ii- f,iii -b,iv – d, v-a
4. i – a,ii- b,iii- c,iv – d, v – e

Answer: 1

42. Assume figure AB \\ CD and EF is the transversal. If angle AGH = 60° what is the measure of angle CHF?

1. 60°
2. 120°
3. 180°
4. 170°

Answer: 2

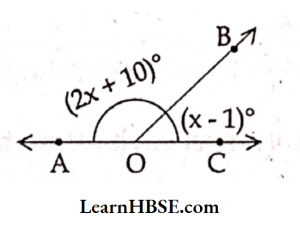
43. If the angles (2a – 10)° and (a -11)° are supplementary, what is the value of a?

1. 47°
2. 57°
3. 67°
4. 37°

Answer: 3

44. One angle of an equilateral triangle is

1. 90°
2. 80°
3. 180°
4. 60°

Answer: 4

45. Which figure shows linear pair?

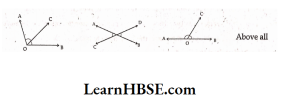
Answer: 3

46. The value of right angle is

1. 180°
2. 90°
3. 0°
4. 50°

Answer: 2

47. What is the measure of ∠z if ∠x = 70°?

1. 120°
2. 130°
3. 110°
4. 140°

Answer: 3

48. If x- y = 80° what are x and y ?

1. 100°, 80°
2. 130°, 50°
3. 50°, 130°
4. 80°, 100°

Answer: 2

49. The number of all possible line segments in the figure ……..

1. 6
2. 4
3. 3
4. 12

Answer: 1

50. Identify the figure in which ‘n’ is transversal.

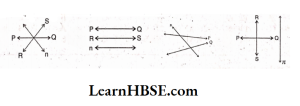
Answer: 3

51. Which pair of the following are complementary angles?

1. 70°, 30°
2. 48°, 52°
3. 70°, 20°
4. 35°, 55°

Answer: 3

52. Which pair of the following are supplementary angles?

1. 110°, 50°
2. 100°, 80°
3. 105°, 65°
4. 45°, 45°

Answer: 2

53. In the given figure

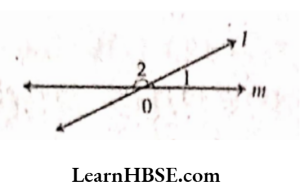
[1 = 30°] then [2=?]

1. 30°
2. 60°
3. 120°
4. 150°

Answer: 4

Haryana Board Class 7 Maths Solutions For Chapter 5 Fill in the blanks :

54……….is formed when lines or line segments meet.

Answer: Angle

55. ………….. angles have a common vertex and a common arm but no common interior points.

Answer: Adjacent

56. When two lines intersect, the vertically opposite angles so formed are………..

Answer: equal

57. When lines drawn on a sheet of paper do not meet, they are………..lines.

Answer: parallel

58. When a transversal cuts two lines such that pairs of interior angles on the same side of the transversal are supplementary, the lines have to be………………

Answer: parallel

59. Match the following:

1.30°,60°                                                                                                                   (  ) A) Supplementary angles
2. 100°, 80°                                                                                                               (  ) B) Linear pair
3. Adjacent and supplementary                                                                             (  ) C) Parallel lines
4. Linesl and m intersect at 0, then the lines are called                                       (  ) D) Complementary angles
5. If there is no common point to the linesl and m, then the lines are called   (  ) E) Intersecting lines

Answer:

1. D 2. A 3. B 4. E 5: C