Haryana Board Class 7 Maths Solutions For Chapter 6 The Triangle and its Properties

Key Concepts

• Triangle:
  A triangle is a simple dosed curve made of three line segments.lt has three vertices, three sides and three angles.

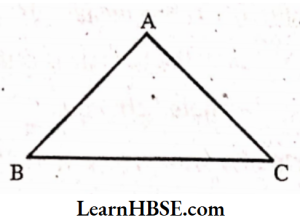
Here is Δ ABC. It has

• 1. Sides: AB’ BC’ CA
  2. Angles:∠BAC, ∠ABC, ∠BCA
  3. Vertices: A, B, C
• The side opposite to the vertex A is BC.
  The angle opposite to the side AB is ∠BCA.
• Classification of Triangles:

1. Based on sides:
   
2. 1. 1. A triangle having three unequal sides is called a scalene triangle.
      2. A triangle having two equal sides is called an isosceles triangle.
      3. A triangle having three equal sides is called an equilateral triangle.
   2. Based on angles:
      1. If each angle is less than 90°,’ then. the triangle is called an acute-angled triangle.
      2. If any one of the angle is a right angle, then the triangle is called a right-angled triangle.
      3. If any one angle is greater than 90°, then the triangle is called an obtuse angled triangle.

• Parts of a Triangle: In a ΔABC,

1. 1. The points A, B, C are called “Vertices”
   2. The line segments AB, BC, CA are called “Sides”.
   3. ∠BAC, ∠ABC, ∠ACB or briefly∠A, ∠B, ∠C are called “angles” of the triangle. The sides AB, BC, CA and the angles ∠A, ∠B, ∠C are called the “Parts of the triangle ABC” or “elements of  ΔABC. “

• In A ABC, we have

1. 1. ∠A is the angle opposite to the side BC
   2. Similarly, ∠B, ∠C are the angles opposite to the sides CA, AB respectively.
   3. A, B, C are the vertices opposite to the sides BC,CA, AB respectively. O The length of the side AB is denoted by AB. i.e., AB is a number.

• Interior and Exterior of a Triangle:

1. 1. The Region of the plane enclosed by A ABC is called the interior of A ABC
   2. The total region of the plane not enclosed by A ABC is called the exterior of A ABC.

Triangular Region: The interior of a triangle together with its boundary is known as the “triangular region ” in a plane.

Haryana Board Class 7 Maths Solutions For Chapter 6 The Triangle and its Properties

1. Write the six elements (i.e., the 3 sides and the 3 angles) of ΔABC.

Solution:

Sides: AB, BC, CA

Angles: ∠A, ∠B,∠C

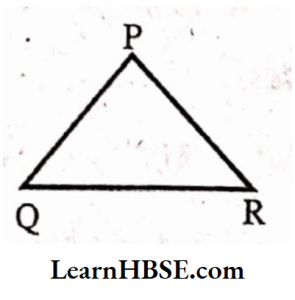
2. Write the:

1. Side opposite to the’ vertex Q of ΔPQR

Solution:

PR

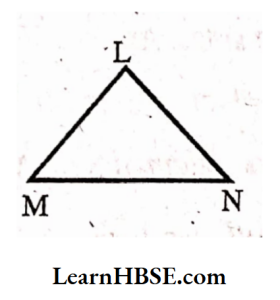
HBSE Class 7 Triangle and Its Properties Solutions

2) Angle opposite to the side LM of ΔLMN

Solution:

∠MNL

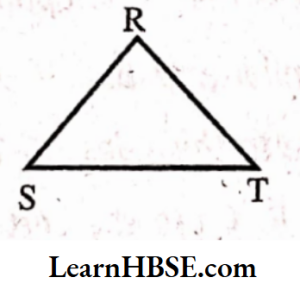
Haryana Board Class 7 Maths Lines and Angles solutions

3) Vertex opposite to the side RT of ΔRST

Solution: S

3. Look at the following figure and classify each of the triangles according to its

1) Sides

2) Angles

1)

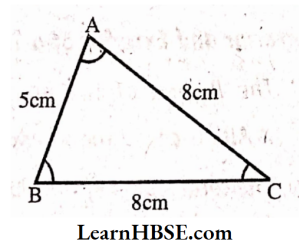
Solution:

Here ΔABC bas two equal sides.

Z It is an isosceles triangle.

Three angles are acute.

It is an acute-angled triangle.

2)

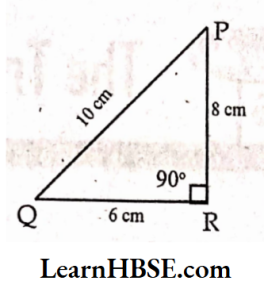
Solution:

In ΔPQR no two sides are equal.

It is a scalene triangle.

One angle is 90°.

It is a right- angled triangle.

Key Questions in Triangles for Class 7 HBSE

3)

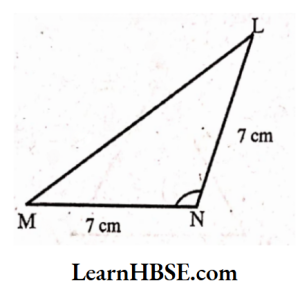
Solution:

In MNL two sides are equal.

It is an isosceles triangle.

One angle is greater than 90°.

It is an obtuse-angled triangle

4)

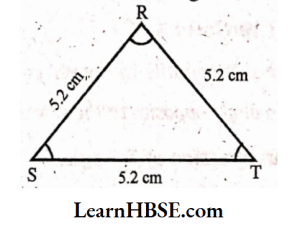
Solution:

In ΔRST, all,three sides are equal.

It is an equilateral triangle.

Ali angles are acute.

It is an acute-angled triangle.

5)

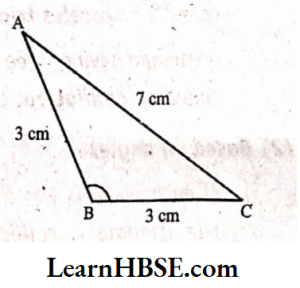
Solution: AABC has two sides equal.

It is an isosceles triangle.

∠B is greater than 90°.

Itis an obtuse-angled triangle.

Haryana Board Class 7 Maths Triangle Properties solutions

6)

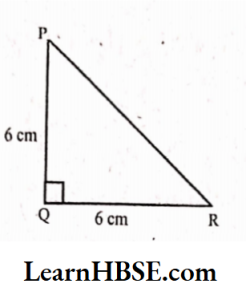
Solution:

ΔPQR has two sides equal.

It is an isosceles triangle.

∠Q is 90°.

It is a right-angled triangle.

1. How many medians can a triangle have?

Solution: A triangle can have three medians.

2. Does a median lie wholly in the interior of the triangle? (If you think that this is not true draw a figure to show such a case).

Solution: Yes, a median lies wholly in the interior of the triangle.

1. How many altitudes can a triangle have?

Solution: A triangle can have three altitudes.

2. Drawrough sketches of altitudes from A to BC for the following triangles.

 

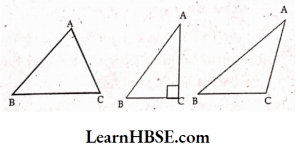
Acute – angled
Right-angled
Obtuse- angled

Solution:

3. Will an altitude always lie in the in terior of a triangle? If you think that this need not be true, draw a rough sketch to show such a case.
Solution:

No, an altitude always does not lie in the interior of a triangle. In the case of an obtuse-angled triangle, the altitude lies in the exterior of the triangle. ABC is an obtuse-angled triangle, zcis obtuse angle. The altitude AL drawn from A on to the produced BC lies in the exterior of the triangle.

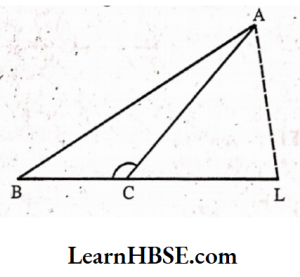
Practice Problems Triangles Class 7 Haryana Board

4. Can you think of a triangle in which two altitudes of the triangle are two of its sides?

Solution:

No, we cannot think of a triangle in which two altitudes of the triangle are the two sides of triangle in the case of an acute-angled triangle and obtuse-angled triangle. Butin the case of rightangled triangle the two altitudes of the triangle areits two sides forming aright angle.

Angle sum property of a triangle Class 7 HBSE

5. Can the altitude and median be same for a triangle?
Solution:

Yes, the altitude and median can be same for an equilateral triangle

Take several cut-outs of (1) an equilateral triangle (2) an isosceles triangle and (3) a scalene triangle. Find their altitudes and medians. Do you find anything special about them? Discuss it with your friends.

Solution: Students can arrangeit with the help of their teacher. At last they find the altitude and median of a triangle are samein an equilateral triangle.

Haryana Board Class 7 Maths Solutions For Chapter 6 Exercise-6.1

1. In ΔPQR, D is the mid-point of QR.

PM is_____.
PD is_______.
Is QM = MR ?

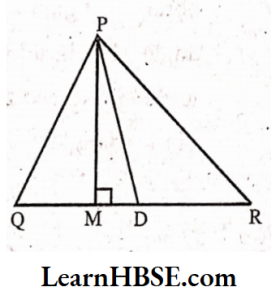
PM is an altitude.

PD is median.

No, QM x MR because M is not the mid point of QR.

2. Draw rough sketches for the following:

(a) In ΔABC, BE is a median.

(b) In ΔPQR, PQ and PR are altitudes of the triangle.

(c) In ΔXYZ, YL is an altitude in the exterior of the triangle

Solution:

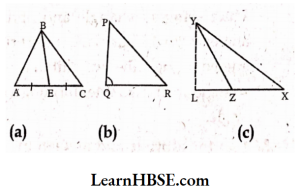
3. Verify by drawing a diagram if the median and altitude of an isosceles triangle can be same.

Solution:

ABC is an isosceles triangle.
AB = AC
P is the mid-point of BC.
AD is the median.
AL is perpendicular to BC.

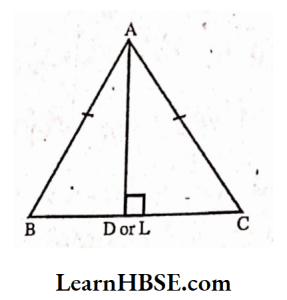
In an isosceles triangle, the median and the altitude are same. AD = AL

1. Exterior angles can be formed for a triangle in many ways. Three of them are shown here.

There are three more ways of getting exterior angles. Try to produce those rough sketches.

Solution: The three more ways of getting exterior angles are :

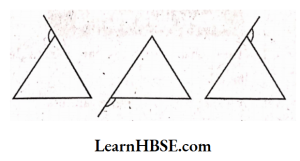
Important Concepts Triangles Class 7 HBSE

2. Are the exterior angles formed at each vertex of a triangle equal?

Solution:

Yes, the exterior angles formed at each vertex of a triangle are equal.

3. What can you say about the sum of an exterior angle of a triangle and its adjacent interior angle?

Solution:

The sumof an.exterior angle ofa triangle and its adjacent interior angle is 180°.

1. What can you say about each of the interior opposite angles, when the exterior angle is

1) aright angle?
2) an obtuse angle?
3) an acute angle?

Solution:

1) If the exterior angle is a right angle, then each of theinterior opposite angle is acute.

2)If the exterior angleis an obtuse angle,then at least one of the interior opposite angle is acute.

3)If the exterior angleis an acute angle,then each of the interior opposite angle is acute.

Exterior angle theorem for triangles Class 7 HBSE

2. Can the exterior angle of a triangle be a straight angle?

Solution:

No, the exteriorangle ofa triangle cannot be a straight angle

1. An exterior angle of a triangle is a measure of 70° and one of its interior opposite angles is of measure 25°. Find the measure of the otherinterior opposite angle.

Solution:

Let the measure of the other interior angle be x.

By exterior angle property of a triangle,

25° + x = 70°

x= 70°- 25°

x = 45°

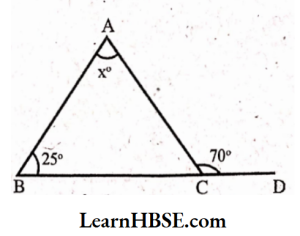
The measure of the other interior opposite angle = 45°.

2. The two interior opposite angles of an exterior angle of a triangle are 60° and 80°. Find the measure of the exterior angle.

Solution:

Given:

The two interior opposite angles of a triangle are 60° and 80°.

Measure of the exterior angle = Sum of its two interior opposite angles.

= 60° +80°=140°

3. Is something wrong in this diagram? Comment.

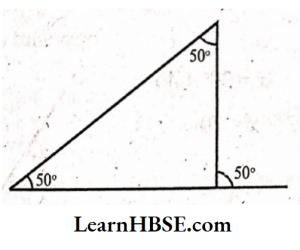
Solution. We know that

Measure of the exterior angle = Sum of its two interior opposite angles

= 50° + 50° = 100°

Given exterior angle of a triangle = 50°

Such a triangle cannot be drawn.

Haryana Board Class 7 Maths Solutions For Chapter 6 Exercise-6.2 :

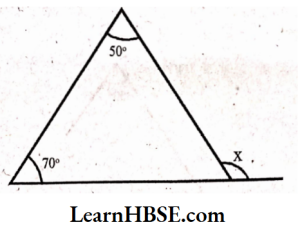
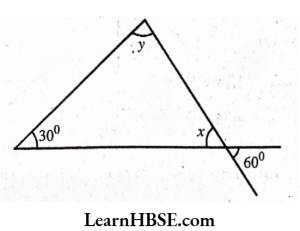
1. Find the value of the unknown exterior angle x in the following diagrams:
Solution:

1) Exterior angle = Sum of the interior opposite angles

x = 50° + 70°

x=120°

2) Exterior angle = Sum of the interior opposite angles

x = 65°+ 45°

x= 110°

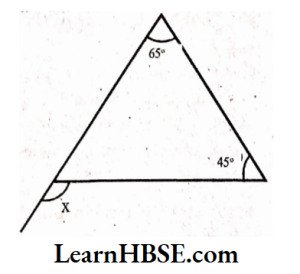
3) Exterior angle = Sum of the interior opposite angles

x = 30° + 40°

x = 70°

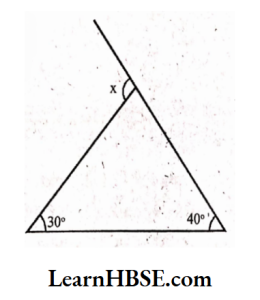
4) Exterior angle = Sum of the interior opposite angles

x = 60° + 60°

x = 120°

Important questions on triangles Class 7 HBSE Maths

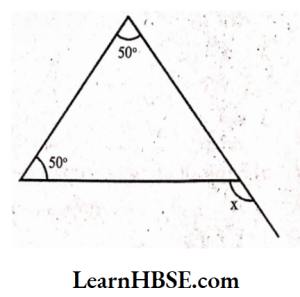
5) Exterior angle = Sum of the interior opposite angles

x = 50° + 50°

x = 100°

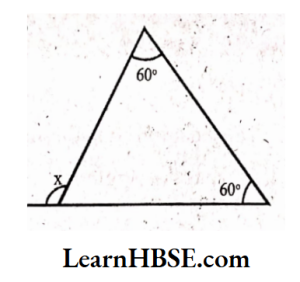
6) Exterior angle = Sum of the interior opposite angles

x = 30° + 60°

x = 90°

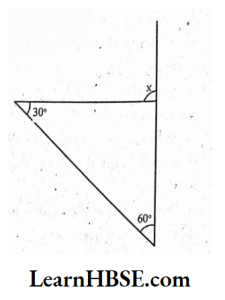
2. Find the value of the unknown interior angle x in the following figures:

Solution:

1) Sum of interior opposite angles = Exterior angle

x +50° = 115°

x = 115°-50°

x = 65°

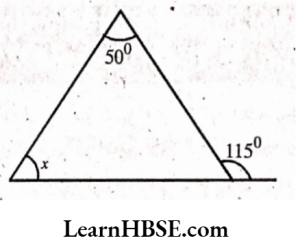
2) Sum of interior opposite angles = Exterior angle

70° + x =100°

x = 100°-70°

x=30°

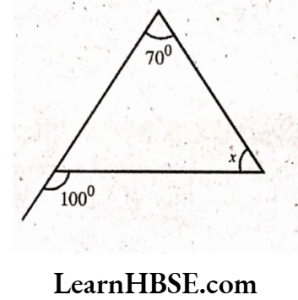
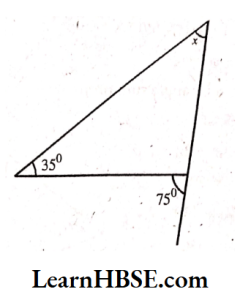
3) Sum of interior opposite angles = Exterior angle

x + 90° = 125°

x =125° -90°

x = 35°

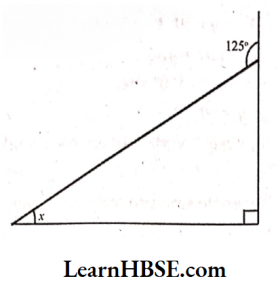
4) Sum of interior opposite angle = Exterior angle

x + 60° = 120°

x = 120°- 60°

x = 60°

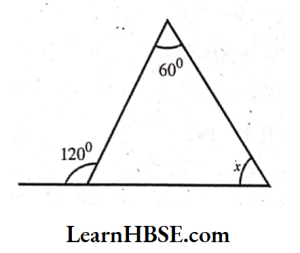
5) Sum of interior opposite angles = Exterior angle

x + 30° = 80°

x = 80°- 30°

x = 50°

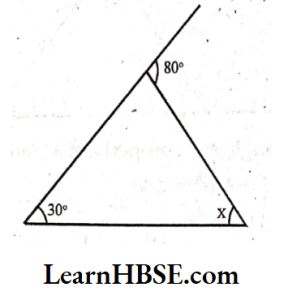
6) Sum of interior opposite angles = Exterior angle

x + 35° = 75°

x =75° -35°

x = 40°

Haryana Board Class 7 Maths Solutions For Chapter 6 Exercise-6.3 :

1. Find the value of the unknown x in the following diagrams:

Solution:

1) By angle sum property,

x + 50°+60° = 180°

x + 110° = 180°

x = 180°-110°

x = 70°

2) By angle sum property,

90° + x + 30° = 180°

120° + x= 180°

x= 180°- 120°’

x=60°

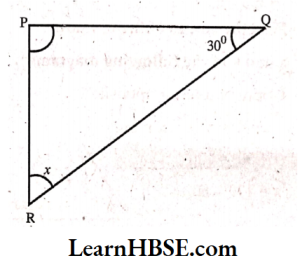
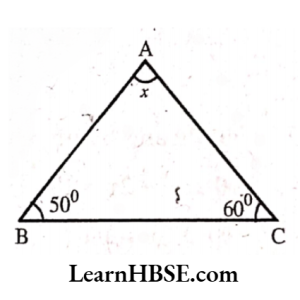
3) By angle sum property

30° + 1109 + x = 180°

140°+x =180°

x=180°- 140°

x = 40°

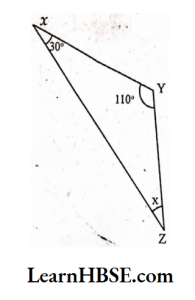
4) By angle sum property

50° + x + x = 180°

50° + 2x = 180°

2x =180°- 50°

2x = 130°

\(x=\frac{130^{\circ}}{2}=65^{\circ}\)

x = 65°.

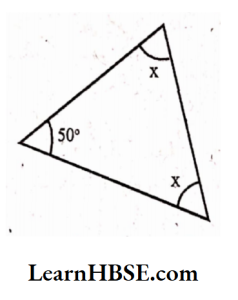
5) By angle sum property

x+x+x= 180°

3x= 180°

\( x=\frac{180^{\circ}}{3} \)

x = 60°

6) By angle sum property,

90° + x + 2x = 180°

90° + 3x= 180°

3x =180°- 90°

3x = 90°

\( x=\frac{90^{\circ}}{3}=30^{\circ} \)

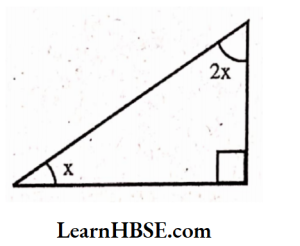
x=30°

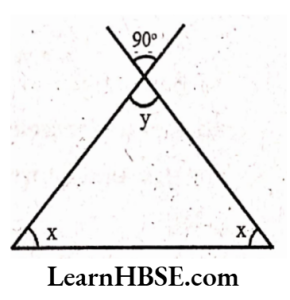
2. Find the values of the unknowns x and yin the following diagrams:

Solution:

1) Sum of interior opposite angles = exterior angle

x + 50° = 120°

x = 120°-50°

x = 70°

 

By angle sum property of a triangle,

x + y + 50° = 180°

700 + y +50° = 180°

y + 120° = 180°

y= 180° -120° = 60°

y – 60°

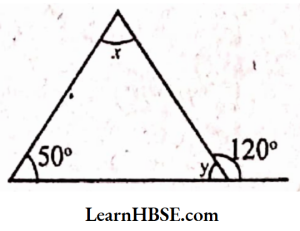
2) y = 80°(vertically opposite angles are equal)

By angle sum property of a triangle,

x + y + 50° = 180°

x + 80° + 50° = 180°

x + 130° = 180°

x = 180° – 130°

x = 50°

3) Exterior angle = Sum of interior opposite angles

x =50° + 60°

x = 110°

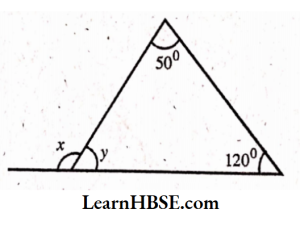
By angle sum property of a triangle,

y + 50° + 60° = 180°

y+ 110°=180°

y= 180° -110°

y = 70°

4) x= 60°(vertically opposite angles are equal.)

By angle sum property of a triangle,

x + y + 30° = 180°

60°+ y + 30° = 180°

y + 90° = 180°

y =180°- 90°

y = 90°

5) y = 90° (vertically opposite angles are equal.)

By angle sum property of a triangle,

x + x + y = 180°

2x + 90° = 180°

2x = 180° -90°

2x = 90°

\( x=\frac{90^{\circ}}{2} \)

x=45°

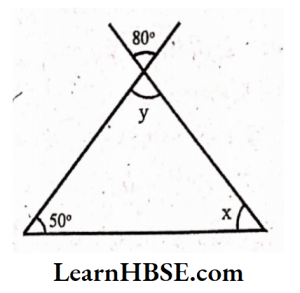
6) x = y (vertically opposite angles are equal)

By angle sum property of a triangle.

x+x+x =180°

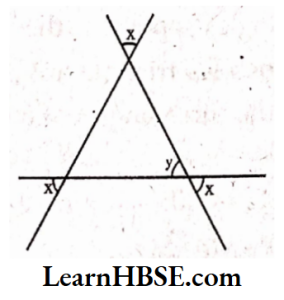
3x = 180°

\( x=\frac{180^{\circ}}{3}=60^{\circ} \)

x = 60°; y = 60°

HBSE Class 7 Maths Chapter 6 Guide

1. Two angles of a triangle are 30° and 80°. Find the third angle.

Solution: Let the third angle be x

By angle sum property of a triangle,

x +30° + 80° = 180°

x+ 110° = 180°

x = 180°- 110°

x = 70°

v. The third angle is 70°.

2. One of the angles of a triangle is 80° and the other two angles are equal. Find the measure of each of the.equal angles.

Solution: Let the measure of the equal angles be x.

By angle sum property of a triangle,

x + x + 80° = 180°

2x + 180° = 80°

2x. =100°

\( x=\frac{100^{\circ}}{2}=50^{\circ} \)

The measure of eachof the equal angle is 50°.

3. The three angles of a triangle arein the ratio1:2:1. Find all the angles of the triangle. Classify the triangle in two different ways.

Solution: Let the three angles of a triangle be x, 2x, x,

By angle sum property of a triangle,

x + 2x + x = 180°

4x = 180°

\( x=\frac{180^{\circ}}{4}=45^{\circ} \)

Three angles of the given triangle are 45°, 45° x 2, 45° or 45°, 90°, 45°

Classification:

1) The triangleis aright-angled triangle.

2) The triangle is an isosceles triangle.

1. Can you have a triangle with two right angles?

Solution: No, we can never have a triangle with two right angles because in a triangle the sum of three angles is 180°.

2. Can you have a triangle with two obtuse angles?

Solution: No, we can never have a triangle with two obtuse angles because in a triangle the sum of three angles is 180°.

3. Canyouhave a triangle with two acute angles?

Solution: Yes, we can have a triangle with two acute angles.

4. Can you have a triangle with all the three angles greater than 60°?

Solution: No, we cannot have a triangle with all the three angles greater than 60°.

5. Can you have a triangle with all the three angles equal to 60°?

Solution: Yes, we can have a triangle with all the three angles equal to 60°.

6. Can you have a triangle with all the three angles less than 60°?

Solution: No, we cannot have a triangle with all the three angles less than 60°.

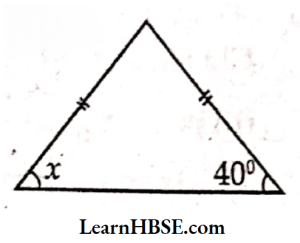
1. Find angle x in each figure:

Solution:

1) Given triangle is an isosceles triangle.

In this triangle, base angles opposite to the equal sides are equal.

x = 40°

2) In an isosceles triangle, base angles opposite to the equal sides are equal. Sum of the three angles of a triangle is 180°.

45° + 45° + x = 180°

90°+ x =180°

x =180°- 90°

x =90°

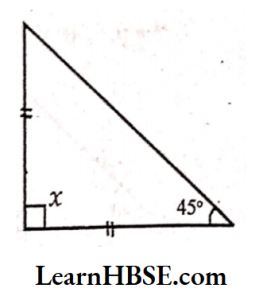
3) In an isosceles triangle, base angles 45° opposite to the equal sides are equal.

x = 50°

4) Base angles opposite to the equal sides of an isosceles triangle are equal.

The sum of the three angles of a triangle is 180°.

x+ x + 100° = 180°

2x = 180°- 100°

2x = 80°

\( x=\frac{80^{\circ}}{2}=40^{\circ} \)

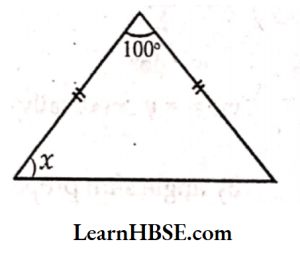
x = 40°

5) Base angles opposite to the equal sides of an isosceles triangle are equal. The sum of the three angles of a triangle is 180°.

x + x + 90° =180°

2x = 180° – 90°

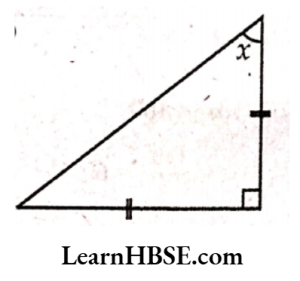
2x = 90°

\( x=\frac{90^{\circ}}{2}=45^{\circ} \)

x = 45°

6) Base angles opposite to the equal sides of an isosceles triangle are equal.

The sum of the three angles of a triangle is 180°.

x + x + 40° = 180°

 

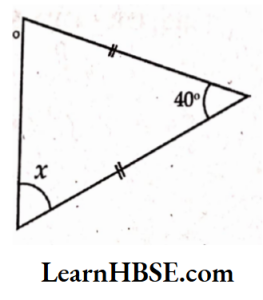
2x = 180°- 40°

2x = 140°

\( x=\frac{88^0}{2}=70^{\circ} \)

x = 70°

7) Base angles opposite.to equal sides of an isosceles triangle are equal. The angles in a linear pair are supplementry.

x+ 120° = 180°

x = 180°- 120°

= 60°

8) Base angles opposite to equal sides of an isosceles, triangle are equal. The external angle of a triangle is equal to the sum ofits interior opposite angles.

x+x= 110°

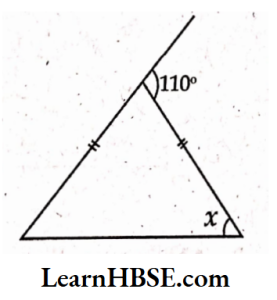
2x = 110°

\( x=\frac{110^{\circ}}{2}=55^{\circ} \)

x = 55°

9) Base angles opposite to equal sides of an isosceles triangle are equal. If two lines intersect, the vertically opposite angles are equal.

= 30°

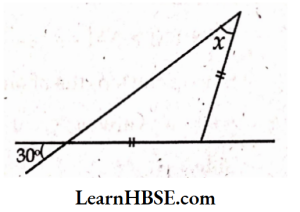
HBSE 7th Class Angle Sum Property Explained

2. Find angles x and y in each figure.

Solution:

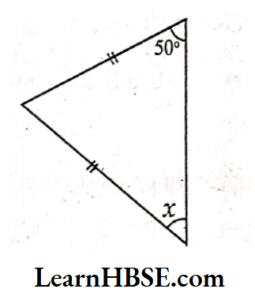
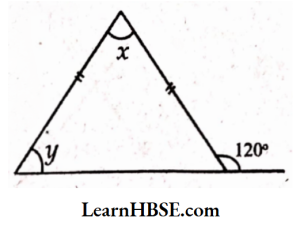
1) Base angles opposite to equal sides of an isosceles triangle are equal.

y + 120°- 180° (Linear pair)

y= 180° -120°

y = 60°

Sum of interior opposite angles = Exterior angle

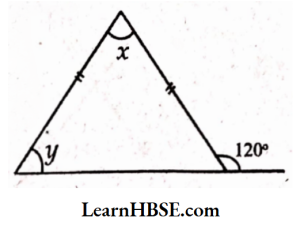
x + y = 120°

x + 60°= 120°

x = 120°- 60° = 60

2) Base angles opposite to the equal sides of an isosceles triangle are equal.

The sum of the measures of the three angles of a triangle is 180°.

x+x + 90° = 180°

2x =180° -90°

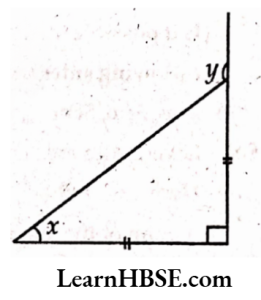
2x = 90°

\( x=\frac{90^{\circ}}{2}=45^{\circ} \)

x = 45°

Exterior angle=Sumof interior opposite angles

y = x + 90°

y = 45° + 90°

y = 135°

3) Base angles opposite to the equal sides of an isosceles triangle are equal. Sum of the measures of the three angles of a triangle is 180°

x + x+92° = 180°

2x = 180° – 92°

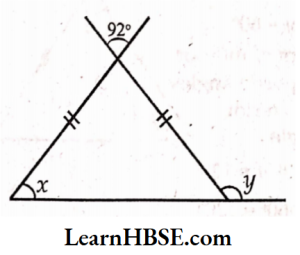
2x = 88°

\( x=\frac{88^{\circ}}{2}=44^{\circ} \)

44° + y = 180° (Linear pair)

y = 180°- 44°

Haryana Board Class 7 Maths Solutions For Chapter 6 Exercise-6.4

1. Is it possible to have a triangle with the following sides?

1) 2cm, 3cm, 5cm

Solution: Given sides are 2cm, 3cm, 5cm

Here 2 + 3 = 5

Sum of the lengths of two sides = Length of the third side

This is impossible.

2) 3cm, 6cm, 7cm

Solution:

Given sides of a triangle are 3cm, 6cm, and 7cm

3 + 6 > 7; 6 + 7 > 3;7 + 3 > 6

Sum of the lengths of any two sides is greater than the length of the third side.

It is possible to form a triangle.

3) 6cm, 3cm, 2cm

Solution:

Given sides of a triangle are 6cm, 3cm,2cm

6 + 3 = 9 > 2; 3 + 2 = 5 |> 6; 2 + 6 = 8 > 3

It is not possible to form a triangle

Sample Problems Triangles Haryana Board Class 7

2. Take any point O in the interior of a triangle PQR. Is

(1) OP + OQ > PQ ?
(2) OQ + OR > QR ?
(3) OR + OP > RP ?

Solution:

1) Yes, OP + OQ > PQ because sum of the lengths of any two sides of ΔPOQ is always greater than the third side.

2) Yes, OQ + OR > QR because sum of the lengths of any two sides of ΔROQ is always greater than the third side.

3) Yes, OR + OP > RP because sum of the lengths of any two sides of ΔROP is always greater than the third side.

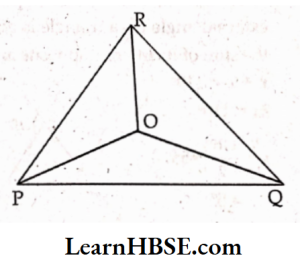
Pythagoras theorem examples Class 7 HBSE

3. AM is a median of a triangle ABC. Is AB + BC + CA > 2 AM ? (Consider the sides of triangles AABM and AAMC)

Solution:

In AABM

AB + BM > AM

Sum of the lengths of any two sides of a triangle is always greater than the third side.

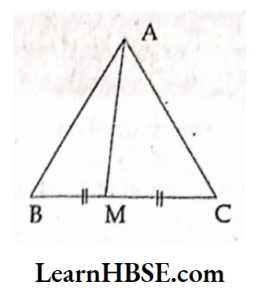
In ΔAMC

CA + CM > AM………(2)

Sum of the lengths of any two sides of a triangle is always greater than the third side.

(1) + (2)

=> (AB + BM) + (CA + CM) > AM + AM

=> AB + (BM + CM) + CA > 2AM

AB + BC + CA > 2 AM

Pythagoras Theorem Class 7 Haryana Board

4. ABCD is a quadrilateral.

Is AB + BC + CD + DA > AC + BD?

Solution: In ΔABC

AB +BC>AC………..(1)

Sum of the lengths of any two sides of a triangle is greater than the length of the third side.

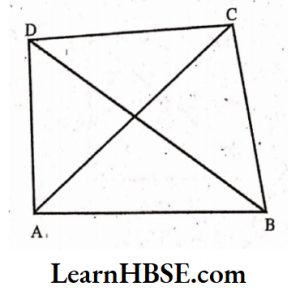
In AACD

CD + DA > AC……….(2)

Sum of the lengths of any two sides of a triangle is greater than the length of the third side.

(1) + (2)

=> AB + BC + CD + DA > AC + AC

AB + BC + CD + DA > 2AC………(3)

In AABD

AB + DA > BD ———(4)

Sum of the lengths of any two sides of a triangle is greater than the length of the third side.

In ABCD

BC + CD > BD——(5)

Sum of the lengths of any two sides of a triangle is greater than the length of the third side.

(4) + (5)

=> AB + DA + BC + CD > BD + BD

AB + BC + CD + DA > 2BD ——(6)

(3) + (6)

=> 2 (AB +BC + CD +DA) > 2AC + 2BD

=> 2 (AB + BC + CD + DA) > 2 (AC + BD)

AB + BC + CD + DA> AC + BD

5. ABCD is quadrilateral. Is AB + BC + CD + DA < 2 (AC + BD) ?

Solution: In quadrilateral ABCD, diagonals AC and BD intersect at O.

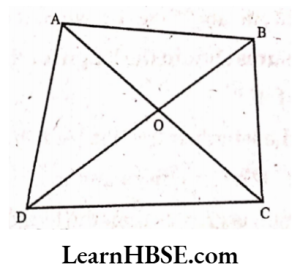
In AOAB

OA + OB > AB

Sum of the lengths of any two sides of a triangle is. greater than the length of the third side.

In AOBC

OB + OOBC

Sum of the lengths of any two sides of a triangle is greater than the length of the third side.

In ΔOCD

OC + OD > CD———-(3)

Sum of the lengths of any two sides of a triangle is greater than the length of the third side.

In ΔOAD

OA+OD>AD———(4)

Sum of the lengths of any two sides of a triangle is greater than the length of the third side.

(1) + (2) (3) + (4)

= (OA + OB) + (OB +OC) + (OC + OD) + (OA + OD) > AB + BC + CD + DA

=>2(OA+OB + OC + OD)> AB + BC + CD + DA

=> 2((OA + OQ + (OB + OD)) > AB + BC+ CD + DA

=> 2(AC + BD) > AB + BC + CD + DA

AB + BC + CD + DA < 2 (AC + BD)

6. The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall ?

Solution: Let the length of the third side be x cm.

Sum of the lengths of any two sides of a triangle is greater than the length of the third side.

Given two sides are 12 cm and 15 cm

12 + 15 > x

27 >x

x < 27

x + 12 > 15

x>15-12

x > 3

x 4 + 15 > 12

x > 12- 15

x > -3

length cannot be negative. The length of the third side should be any where between 3 cm and 27 cm

1. Is the sum of any two angles of a triangle is always greater than the third angle?

Solution: No, the sum of any two angles of a triangle is not always greater than the third angle

Find the unknown length x in the following figures:

1.

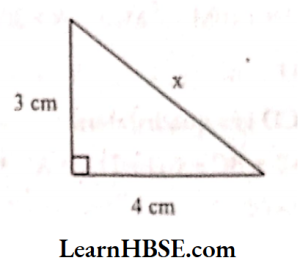
Solution:

By Pythagoras property,

x²- 3² + 4²

X² = 9 + 16

x² = 25

x = √25 => x =5 cm

2.

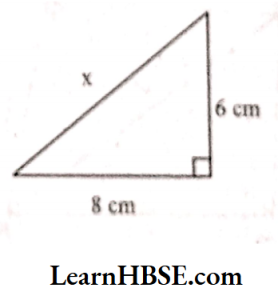
Solution:

By Pythagoras property,

x²= 6² + 8²

x²= 36 + 64

x² = 100

x = √100 => x = 10 cm

3)

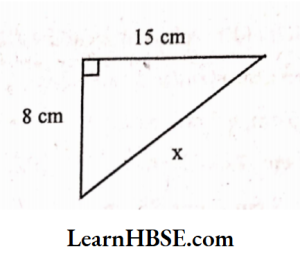
Solution:

By Pythagoras property

x² = 15² + 8²

x² = 225 + 64

x² = 289

x = √289 => x = 17 cm

4.

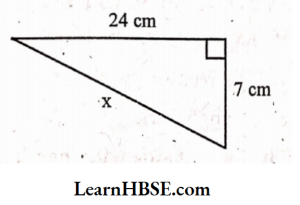
Solution:

By Pythagoras property,

x²= 24² + 7²

x² = 576 + 49

x²= 625

x = √625

x = √25 x 25 = 25 cm

5.

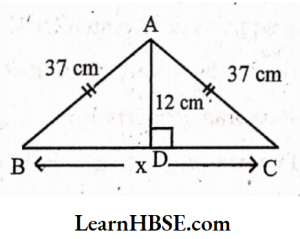
Solution:

ABC is an isosceles triangle.

AB = AC = 37 cm

D is the mid-point of BC

BD = DC

ABD is a right – angled triangle.

By Pythagoras property,

AB² = AD² + BD²

37² = 12² + BD²

∴ BD² =37²-12²

= 1369 -144 = 1225

BD = √1225 = 35 cm

x = BD + DC = 35 + 35 = 70 cm

6)

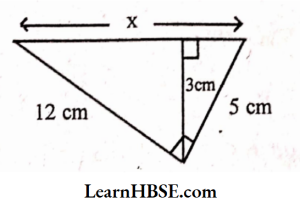
Solution:

By Pythagoras property,

x² = 12² + 5²

x² = 144 + 25

x = √169

x=√169 =13 cm

Haryana Board Class 7 Maths Solutions For Chapter 6 Exercise-6.5 :

1. PQRis a triangle, right-angled at P. If PQ = 10 cm and PR = 24 cm find QR.

Solution:

ΔPQR is a right-angled triangle.

∠P = 90°; PQ = 10 cm; PR = 24 cm.

By Pythagoras property

QR² = PQ² + PR²

= (10)² + (24)²

= 100 + 576

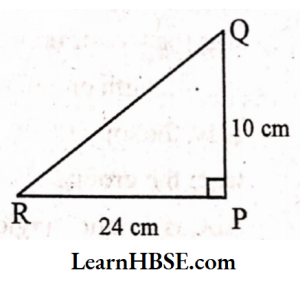
QR² =676

QR = √676 = √26 x 26 = 26 cm

2. ABC is a triangle, right-angled at C.I f AB = 25 cm and AC = 7 cm, find BC.

Solution:

ABC is a right-angled triangle. ∠C = 90°; AB = 25 cm; AC = 7 cm.

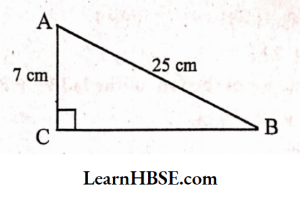
By Pythagoras property,

AB² = AC² + BC²

BC² = AB²- AC²

= (25)²-(7)²

= 625 – 49

BC² = 576

BC= √576

=> BC = √24×24 => BC = 24 cm

3. A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

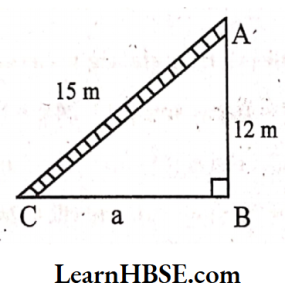
Solution:

Let AC be the ladder.

C is the foot of the ladder.

AC= length of the ladder = 15 m

A be the top of the ladder at 12 m high from the ground.

ABC is a right-angled triangle.

By Pythagoras property,

AC² = AB² + BC²

BC² = AC²- AB²

a² = 15²- 12²

a²= 225-144=a² = 81

=> a = 81 => a = 79×9

a = 9

Distance of the foot of the ladder from the wall is 9 m.

4. Which of the following can be the sides of a right triangle?

1) 2.5 cm, 6.5 cm, 6 cm
2) 2 cm, 2 cm, 5 cm
3) 1.5 cm, 2 cm, 2.5 cm,

In the case of right-angled triangles, identify the right angles.
Solution:

1) 2.5 cm, 6.5 cm. 6 cm

2.5 cm, 6.5 cm, 6 cm.,

(2.5)² + 6² = 6.25 + 36 = 42.25 = (6.5)²

Pythagoras property is satisfied.

The triangle with given sides is right- angled triangle.

The longest side with length 6.5 cm, is the hypotenuse and angle opposite to this side is the right angle.

2) 2 cm, 2 cm, 5 cm

2²+ 2² = 4 + 4 = 8

5² = 25

2² + 2²≠ 52

The squares of two smaller sides is not equal to the square of the third side. Pythagoras property is not satisfied.

The triangle with given sides is not a right – angled triangle.

3) 1.5 cm, 2 cm, 2.5 cm,

(1.5)² + (2)² = 2.25 + 4 = 6.25 = (2.5)²

Pythagoras property is satisfied.

The triangle with given sidesis a right-angled triangle.

The longest side with length 2.5 cm is the hypotenuse. The angle opposite to this side is a right angle.

5. A tree is broken at a height of 5m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.

Solution: Let the original height of the tree be BA and tree broken at C.

BC = 5 cm,

AC = CD (Given)

BD = 12 m

AABC is a right-angled triangle; [B = 90°

By Pythagoras property,

CD² = BC² + BD²

= 5²2 + 12²

= 25 + 144

CD²=169

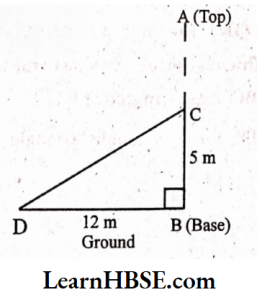
CD = √169 = √13X13

CD = 13 m

AB = BC + CA

= BC + CD

= 5 + 13 = 18 m

The original height of the tree =18m

6. Angles Q andR of a ΔPQR are 25° and 65°. Write which of the following is true:

(1) PQ² + QR² = RP²
(2) PQ²+ RP²= QR²
(3) RP² + QR² = PQ²

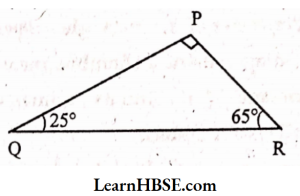
Solution: In APQR,

∠Q = 25°; ∠R = 65° . .

By angle sum property of a triangle,

∠P + ∠Q + ∠R = 180°

∠P + 25° + 65° = 180° .

∠P + 90° = 180°

∴ ∠P= 180° – 90° = 90°

The side opposite to right angle is the hypotenuse.

QR is the hypotenuse.

QR² = PQ² + PR²(By Pythagoras property).

(2) is true.

7. Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.

Solution: ABCD is a rectangle.

AB = 40 cm

Diagonal BD = 41 cm

AABD is a right-angled triangle.

By Pythagoras property,

BD² = AB²+ AD²

AD² = BD²- AB²

= (41)²-(40)²

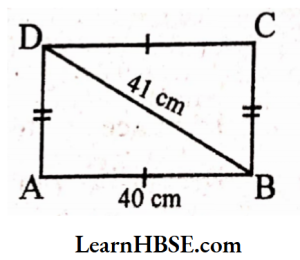
AD²=1681-1600 = 81

AD = √81 => AD = 9 cm

Perimeter of the rectangle ABCD

= 2 (AB+ AD)

= 2 (40 + 9) = 2 X 49 = 98 cm

Perimeter of the rectangle = 98 cm

8. The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.

Solution:

ABCD is a rhombus.

Diagonals AC and BD intersect at O.

AC = 16 cm

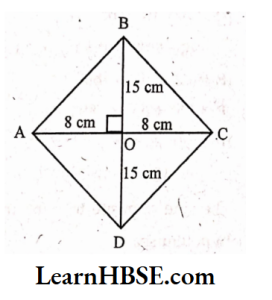
OA = OC = 1/2×16=8cm

BD = 30 cm

OB = OD =1/2 x 30 = 15 cm

AAOB is a right-angle triangle.

∠O=90°

By Pythagoras property,

AB² = OA²+ OB²

AB² = 8² + 15²

= 64 + 225 = 289

AB = √289 = 17 cm

In a rhombus all sides are of equal length.

AB = BC = CD = DA = 17 cm

Perimeter of the rhombus ABCD

= 4 x side

= 4 x17 = 68 cm

Perimeter of the rhombus = 68 cm

1. Which is the longest side in the triangle PQR; right-angled at P?

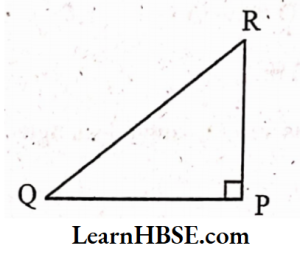
Solution:

In any right-angled triangle the hypotenuse is the longest side.

ΔPQR is a right-angled triangle and right-angled at P.

The side opposite to angle P is QR.

QR is the hypotenuse.

QR is the longest side.

2. Which is the longest side in the triangle ABC, right-angled at B?

Solution:

ABC is a right-angled triangle

∠B = 90°

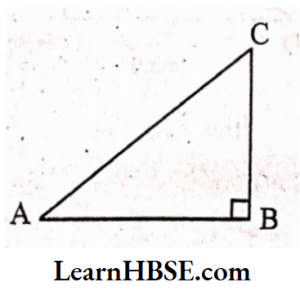
The side opposite to angle B is AC.

AC is the hypotenuse.

AC is the longest side.

3. Which is the longest side of a right triangle ?

Solution:

The hypotenuse is the longest side of a right triangle.

4. ‘The diagonal of a rectangle produce by itself the same area as produced by its length and breadth’-This is Baudhayan Theorem. Compare it with the Pythagoras property.

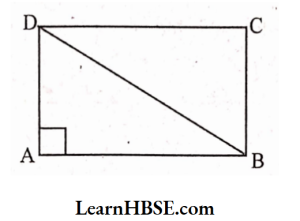
Solution:

ABCD is a rectangle.

BD is the diagonal.

According to the question,

Area produced by the diagonal =

Area producedby the length + Area produced by the breadth

BD² = AB² + AD²

Which is nothing but Pythagoras property.

Haryana Board Class 7 Maths Solutions For Chapter 6 Very Short Answer Questions

1. Write the types of triangles according to sides.
Solution:

(1) Scalene triangle
(2) Isosceles triangle and
(3) Equilateral triangle.

2. Write the types of triangles based on angles.
Solution:

(1) Acute – angled triangle
(2) Obtuseangled triangle and
(3) Right – angled triangle.

3. State ‘Angle -sumproperty of a triangle.

Solution:

The total measure of the three angles of a triangle is 180°.

4. What is meant by altitude of a triangle?

Solution:

The perpendicular line segment from a vertex of a triangle to its opposite side is called an altitude of the triangle.

5. What is meant by ‘hypotenuse’ of a -triangle?
Solution:

In a right – angled’ triangle the side opposite to the right angle is called the hypotenuse.

6. State ‘Pythagoras property’

Solution: In a right- angled triangle the square on the hypotenuse is equal to the sum of the squares on its legs.

7. Write the features of (1) Equilateral triangle and (2) Isosceles triangle.

Solution: (1) A triangle is said to be equilateral, if each one ofits sideshas the same length.

Each angle has measure 60°.

(2) A triangle is said to be isosceles,if at least any two of its sides are of same length. Base angles opposite to the equal sides are equal.

8. Classify the following angles into acute, obtuse and right angles: 20°, 50°, 102°, 47°, 125°, 65°, 36°, 90°, 95° and 110°.

Solution:

Acute angles: 20°, 50°, 47°, 65° and 36°.

Right angle: 90°.

Obtuse angles:102°,125°, 95° and110°.

9. Sum of two interior angles of a triangle is 105°. Find the third angle.

Solution:

Sum of two interior angles of a triangle = 105°

Let the third angle be = x

Sum of three interior angles ofa triangle =180°

=> 105° + x = 180°

=> x = 180° -105°

x = 75°

The third angle = 75°.

10. In ΔPQR, if∠P=65° and ∠Q=50°, then find ∠R.

Solution: In ΔPQR, if ∠P = 65° and ∠Q = 50°.

The sum of three interior angles of a triangle = 180°.

∠P +∠Q + ∠R = 180°.

=> 65° + 50° + ∠R = 180°

115° + ∠R= 180°

∠R= 180° – 115°

∠R= 65°

Haryana Board Class 7 Maths Solutions For Chapter 6 Short Answer Questions

11. Classify the following triangles based on the length of their sides.

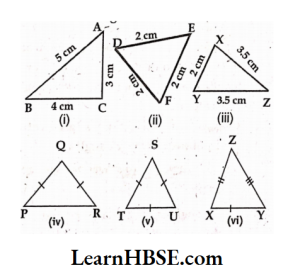
Solution:

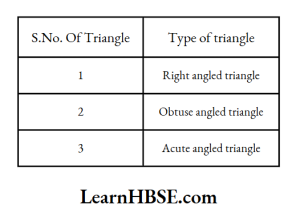
12. Classify the following triangles based on the measure of angles.

(1)

(2)

(3)

Solution:

13. If the three angles of a triangular signboard are 2x, (x- 10)° and (x + 30)° respectively. Then find it’s angles.

Solution: The three angles of a triangular sign board are 2x°, (x- 10)° and (x + 30)° respectively.

The sum of three interior angles of a triangle =180°

2x + x-10 + x + 30 = 180°

=>4x° + 20° = 180°

=>4x° =180° -20°

=> 4x° = 160°

x = \( \frac{160}{4} \)

=>x =40°

First angle = 2x° = 2 X 40° = 80°

Second angle = (x-10)° =40°-10° = 30°

Third angle = x + 30° = 40° + 30° = 70°

14. If one angle of a triangleis 80°, find the other two angles which are equal.

Solution:

If one angle of a triangle = 80°

Given that other two angles are equal.

Let the equal angle be x

The sum of three interior angles of a triangle = 180°

=> 80° + x°+ x° = 180°

=> 80° + 2x° = 180°

=> 2x°=180° – 80°

=> 2x°= 100°

x° = \( \frac{100}{2} \)

=> x = 50°

Other two equal angles are 50° and 50°

15. The angles of a triangle arein the ratio 2: 4: 3, then find the angles.

Solution:

The ratio of angles of a triangle=2:4:3

The sum ofratio = 2 + 4 + 3 = 9

Sum of three interior angles of a triangle =180°

The value of first angle

= \( \frac{2}{9} \) x 180 = 2 x 20° = 40°

The value of second angle

= \( \frac{4}{9} \) x 180 = 4 x 20° = 80°

The value of third angle

= \( \frac{3}{9} \) x 180 = 3 x 20° = 60°

16. What are the measurements of angles of an equilateral triangle?

Solution:

Let ΔABCis an equilateral triangle, then

AB=BC = CA

We know that the angles which are opposite to equal sides are equal.

So ∠A =∠B = ∠G

Let the equal angle = ∠A=∠B=∠C=x°

The sum of three interior angles of a triangle = 180°

∠A + ∠B + ∠C = 180°

=>x° + x° + x° = 180°

=>3x = 180°

x = \( \frac{180}{3} \)

x = 60°

The measurement of each angle of an equilateral triangle is 60°.

17. Which of the following angles form a triangle?

Solution: “If the sum of three interior angles of a triangle is equal to 180°”, then the three angles form a triangle.

1) 60°, 70°, 80°

Solution: Sum of three angles

= 60° +70° + 80° = 210° = 180°

It cannot form a triangle.

2) 65°, 45°, 70°

Solution: Sum of three angles

= 65° + 45° + 70° = 180°

It can form a triangle.

3) 40°, 50°, 60°

Solution: Sum of three angles

= 40° + 50° + 60° = 150° = 180°

It cannot form a triangle.

4) 60°, 30°, 90°

Solution: Sum of three angles

= 60° + 30° + 90° = 180°

It can form a triangle.

5) 38°, 102°, 40°

Solution:

Sum of three angles

= 38° + 102° + 40° = 180°

It can form a triangle.

6) 100°, 30°, 45°

Solution: Sum of three angles

= 100° + 30° + 45° = 175° = 180°

It cannot form a.triangle.

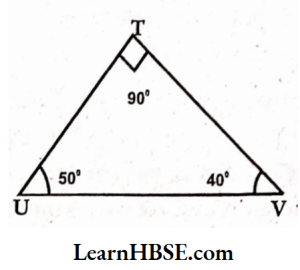
18. Find the missing angles in each of the following triangles.

1)

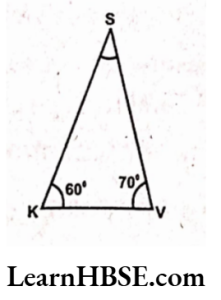
Solution:

The sum of three interior angles of a, triangle = 180°

∠K + ∠V + ∠S = 180°

=> 60° + 70° + ∠S = 180°

=> 130° + ∠S= 180°

=>∠S= 180°- 130°

=> ∠S= 50°

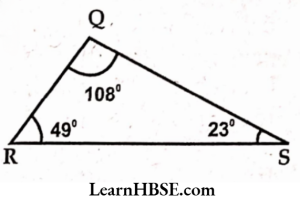
2)

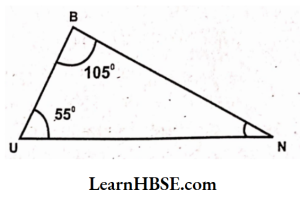
Solution:

The sum of three interior angles of a triangle = 180°

∠B + ∠U+ ∠N = 180°

=> 105° + 55° + ∠N = 180°

160°+ ∠N= 180°

∠N= 180° – 160°

∠N= 20°

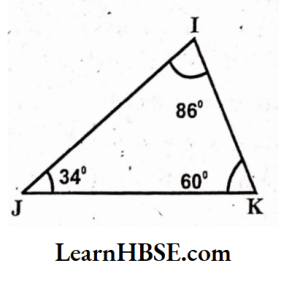
3)

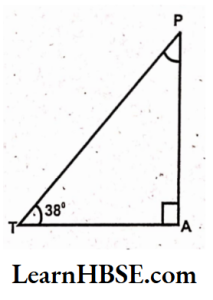
Solution:

The sum of three interior angles of a triangle = 180°

∠A + ∠T + ∠P = 180°

=> 90° + 38° +∠P = 180°

=> 128° +∠P= 180°

=> ∠P= 180° – 128°

=> ∠P = 52°

19. Find the value of ‘x’in the given figure.

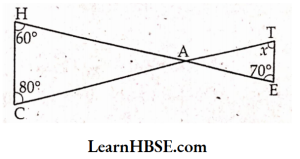
Solution:

From the given figure ∠CAH = ∠TAE

[Vertically opposite angles]

From ΔACH

=> ∠CAH + 60° + 80° = 180°

[ The sum of three interior angles
= 180°]

=> ∠CAH +140° = 180°

=> ∠CAH = 180° -140°

=> ∠CAH = 40°

∠TAE = ZCAH = 40°

From ΔAET

∠TAE +∠AET +∠ATE = 180° ‘

40° + 70° + x = 180°

=> 110° + x° = 180°

=>x°= 180° -110°

x° = 70°

20. Find the value of ‘x’ in the following figures

1)

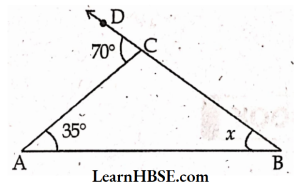
Solution:

From the figure, ∠A = 35°, ∠B = x°

Exterior angle = ∠ACD = 70°

Exterior angle at C = ∠A + ∠B

70° = 35° + x°

( The exterior angle of triangleis equal to sum of its interior angles)

=> 35° + x° = 70° • ‘

=> x° = 70°- 35°

x° = 35°

2)

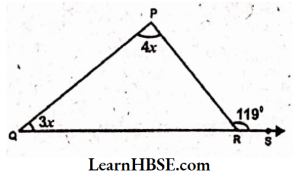
Solution:

From the figure, ∠P = 4x°, ∠Q = 3x°

exterior angle at R = ∠PRS = 119°

exterior angle at R = ∠P + ∠Q

(The exterior angle of triangle is equal to sum of its interior angles)

119° = 4x° + 3x°

=> 119° = 7x°

x = \( \frac{119}{7} \)

= 17° =>x = 17°.

The interior angles 4x = 4 x17 = 68°

3x = 3×17 = 51°.

21. Find the value of V in the following triangles:

1)

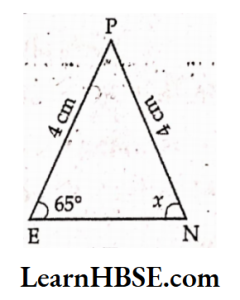
Solution:

From ΔPEN, PE = 4 cm, PN = 4 cm

PE = PN

So it is isosceles triangle. Angles opposite to equal sides are equal
in isosceles triangle.

∠N = ∠E

x =65°

2)

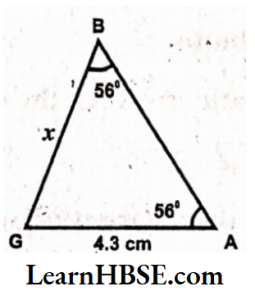
Solution:

From ZABG,ZA = 56°, ZB = 56°

By angle sum property of a triangle

x° + 56° + 56° = 180°

x° + 112° = 180°

x° = 180° – 112°

x = 68°

[The sides opposite to equal angles
are equal.]

=>AG = BG

=>BG = 2 = 4.3 cm

22. Find the value of V and ‘y’ in the adjacent figure

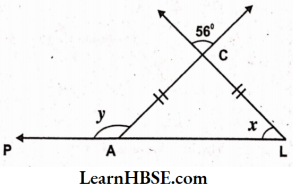
Solution:

From the given figure

∠C = ∠ACL =56° (Vertically opposite angles)

Given that AC = LC. so ΔACL is an isosceles triangle. Angles opposite to equal sides are equal in isosceles triangle.

=> ∠A + ∠L = x°

=> ∠A +∠ C + ∠L = 180°

(By Angle sumproperty of a triangle)

=>x° + 56° +x° = 180°

=> 2x° + 56° = 180°

=> 2x° = 180° – 56°

=> 2x° = 124°

x = \( \frac{124}{2} \)

x = 62°

Now ∠PAC +∠CAL =180°

(Linear pair of angles)

=> y + x = 180°

=> y + 62 = 180°

=> y = 180° – 62°

y = 118°

Haryana Board Class 7 Maths Solutions For Chapter 6 Multiple Choice Question and Answers

 

1. If two angles in a triangle are 75°, 55°, what type of triangle is that ?

1. Obtuse
2. Acute
3. Right
4. Scalene

Answer: 2

2. The ratio in which the centroid of a triangle divides the median is……..

1. 1:2
2. 1:3
3. 2:1
4. 3:1

Answer: 3

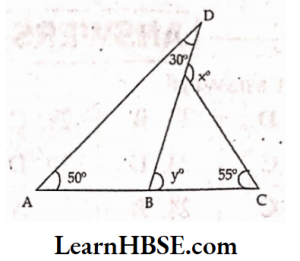
3. From the adjacent figure find the values of x and y.

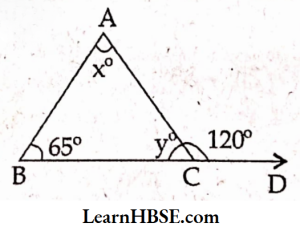
1. x = 65°, y = 60°
2. x = 55°, y = 60°
3. x = 60°, y = 55°
4. x = 60°, y = 65°

Answer: 2

4. The angles of the triangle are in the ratio1:2:3 than the smallest angle is……….

1. 30°
2. 60°
3. 90°
4. 80°

Answer: 1

5. A triangle can have……altitudes.

1. 1
2. 2
3. 3
4. 4

Answer: 3

6. The exterior angle of a triangle is 130° and one of its interior opposite angle is 60°,then the other opposite interior angle is

1. 60°
2. 80°
3. 70°
4. 50°

Answer: 3

7. If in a triangle two angles are equal and the third angle is 120°, what are the equal angles?

1. 40°, 40°
2. 30°, 30°
3. 20°, 20°
4. 50°, 50°

Answer: 2

8. Find x and y values from the figure.

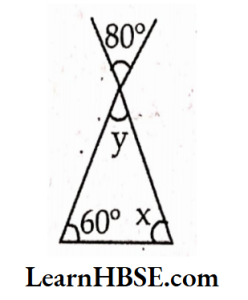
1. x = 40°, y = 80°
2. x = 80°, y = 40°
3. x = 70°, y ~ 60°
4. x = 80°, y = 70°

Answer: 1

9. An obtuse angled triangle has……. acute angles.

1. one
2. two
3. three
4. zero

Answer: 2

10. The angle in an equilateral triangle is

1. 70°
2. 50°
3. 60°
4. 40

Answer: 3

11. In a right-angled isosceles triangle the acute angle is

1. 30°
2. 40°
3. 50°
4. 45°

Answer: 4

12. An acute angled triangle has acute angles.

1. 1
2. 2
3. 3
4. 4

Answer: 3

13. A triangle which has maximum two acute anglesis

1. Obtuse
2. Right
3. A and B
4. None

Answer: 3

14. The following are acute angled triangles

1. Equilateral
2. Isosceles
3. Scalene
4. Above all

Answer: 4

15. The following is the possible third side if the two sides are 6 cm, 9 cm

1. 1 cm
2. 2 cm
3. 3 cm
4. 6 cm

Answer: 4

16. Choose the correct matching. ( )
i) AB + BC> ( ) a) BC
ii) BC- CA < ( ) b) CA
iii) AD is altitude, then AD < ( ) c) AB

1. i-a, ii-b,iii-c
2. i-b, ii-a, iii-c
3. i-b, ii-c, iii-a
4. i-c, ii-b, iii-a

Answer: 3

17. The altitude of the …………………triangle lies outside of the triangle.

1. Acute angled
2. Right-angled
3. Obtuse angled
4. Scalene

Answer: 3

18. What is ‘x’ here?

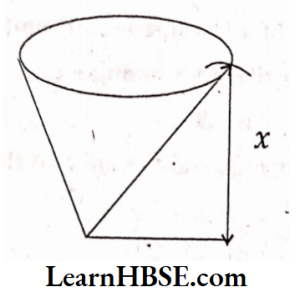
1. Median
2. Radius
3. Altitude
4. Angular bisector

Answer: 3

19. In ΔABC if ∠A = 3, ∠B and ∠C = 2 ∠B. find all the three angles of ΔABC.

1. 90°, 60°,30°
2. 60°, 60°, 60°
3. 90°, 45°, 45°
4. 50°, 40°, 90°

Answer: 1

20. In adjacent figure x °=

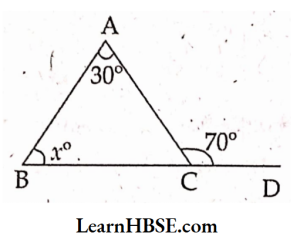
1. 70°
2. 30°
3. 100°
4. 40°

Answer: 4

21. Which of the following are the possible sides of a triangle ?

1. 3 cm, 5 cm, 10 cm
2. 4 cm, 4 cm, 8 cm
3. 3 cm, 4 cm, 5 cm
4. None of these

Answer: 3

22. If the three angles of a triangle are in the ratio 1:2:3, then the angles are

1. 40°, 60°, 80°
2. 30°, 60°, 90°
3. 50°, 100°, 150°
4. 30°, 50°, 100°

Answer: 2

23. In ΔXYZ, ∠X =30°, ∠Y = 45° then find ∠Z

1. 75°
2. 15°
3. 95°
4. 105°

Answer: 4

24. In the given figure, the values of x + y is

 

1. 120°
2. 190°
3. 110°
4. 180°

Answer: 2

25. Angles of a triangle are 30°, 110°, x° then x is

1. 50°
2. 40°
3. 60°
4. 15°

Answer: 2

26. The lengths of two sides of an isosceles triangle are 7 cm, 8 cm then the possible third side is of length

1. 7 cm
2. 9 cm
3. 8 cm
4. 7 or 8 cm

Answer: 4

27. The exterior angle of an equilateral triangle is

1. 60°
2. 120°
3. 150°
4. 90°

Answer: 2

28. If the angles of a triangle arein the ratio 3:1:2, then biggest angle is

1. 60°
2. 120°
3. 90°
4. 30°

Answer: 3

29. The two angles of a triangle are complementary thenit is …..triangle.

1. Acute angled
2. Obtuse angled
3. Right angled
4. Equilateral

Answer: 3

30. Find x in the figure

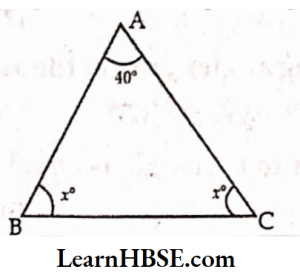
1. 40°
2. 60°
3. 50°
4. 70°

Answer: 4

31. Find Z in the figure

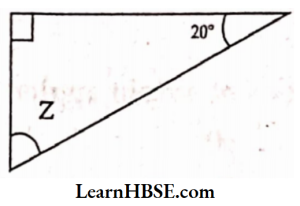
1. 70°
2. 60°
3. 50°
4. 40°

Answer: 1

32. In a ΔPQR,if ∠P = 100° and ∠Q = ∠R then ∠P + ∠R =

1. 100°
2. 180°
3. 140°
4. 40°

Answer: 3

33. Choose the correct matching.

i) 60°, 60°, 60° ( ) a) Obtuse angled triangle
ii) 45°, 45°, 90° ( ) b) Isosceles triangle
iii) 100?, 40°, 40°( ) c) Right angled triangle
iv) 90°,30°,60° ( ) d) Equilateral triangle
v) 50°, 50°, 80° ( ) e) Right angled isosceles triangle

1. i – a,ii-b,iii – c,iv – d, v – e
2. i – d,ii – e,iii – a, iv – c, v -b
3. i- c,ii- d,iii – e,iv – a, v -b
4. i – e,ii – d,iii – c, iv -b, v – a

Answer: 2

34. Least number of possible acute angles in a triangle is …

1. 1
2. 2
3. 3
4. 0

Answer: 2

35. Which type of triangle is formed by BC = 7.2 cm, AC = 6 cm and ∠C = 120°?

1. An acute angled triangle
2. An obtuse angled triangle
3. A right angled triangle
4. An isosceles triangle

Answer: 2

36. Which triangle is formed by AB = 3 cm, BC = 4 cm and AC = 8 cm ?

1. A scalene triangle
2. An isosceles triangle
3. An equilateral triangle
4. No triangle is formed

Answer: 4

37. P: An isosceles triangle is right-angled. Q: ∠A = ∠B = 45° and ∠C = 90° Which of the following statements is true?

1. P is true and Q is not the correct explanation of P.
2. P is false.
3. Q is true and P is the correct explanation of Q.
4. P is true and Q is the correct explanation of P.

Answer: 4

38. Which of the following statements is not true?

1. A triangle can have three 60° angles.
2. A triangle can have a right angle.
3. A triangle can have two right angles.
4. A triangle can have all three angles equal.

Answer: 3

39. Which of the following angles are not the angles of a triangle ?

1. 45°, 65°, 70°
2. 45°, 55°, 65°
3. 60°, 60°, 60°
4. 30°, 60°, 90°

Answer: 2

40. Sum of interior angles in a triangle is equal to

1. Two right angles
2. Two straight angles
3. Right angle
4. 0°

Answer: 1

41. Sum of two acute angles of a right angled triangle is

1. 90°
2. 30°
3. 60°
4. 180°

Answer: 1

42. In ΔABC, which of the following is false ?

1. AB-BC< AC,
2. BC + CA>AB ‘
3. AB-BC=AC
4. None

Answer: 3

43. A triangle can have………….obtuse angle.

1. 0
2. 1
3. 2
4. 3

Answer: 2

44. The relation between x and y in the given figure expressed with ‘y’ as subject is

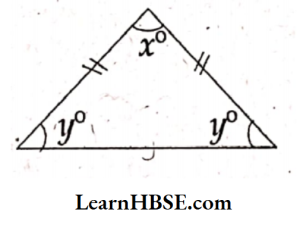
1. 2y = 180 + x
2. \(y=\frac{1}{2}(180+x)\)
3. 2y = 180- x
4. x = 180 + 2y

Answer: 3

45. Following lengths of the sides of a triangle are given.In which case it is not possible to construct a triangle? (in cms)

1. 3,4,5
2. 6,6,6
3. 4,4,8
4. 3,5,7

Answer: 3

46. The sum of interior angles in a pentagon is

1. 270°
2. 360°
3. 540°
4. 480°

Answer: 3

47. The opposite interior angles are in the ratio1: 4, then ∠A, ∠B = ?

1. 26°, 104°
2. 104°, 26°
3. 75°, 105°
4. 50°, 80°

Answer: 1

48. In the adjacent figure ∠A +∠B + ∠C + ∠D + ∠E =

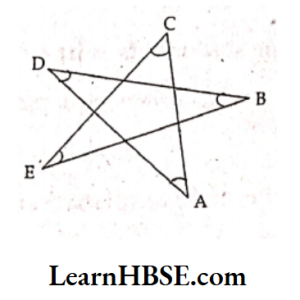
1. 90°
2. 360°
3. 270°
4. 540°

Answer: 2

49. Find the values of x and y

1. 135°, 80°
2. 80°, 135°
3. 70°, 125°
4. 125°, 70°

Answer: 1

50. The following is the representation of line segment.

1. AB
2. AB
3. AB
4. AB

Answer: 3

51. Name the triangle with length 7cm, 8 cm, 9cm.

1. Equilateral
2. Isosceles
3. Scalene
4. Right-angled triangle

Answer: 3

52. The measure of right angle is

1. 90°
2. 100°
3. 180°
4. 80°

Answer: 1

53. Each angle in an equilateral triangle is

1. 30°
2. 45°
3. 80°
4. 60°

Answer: 4

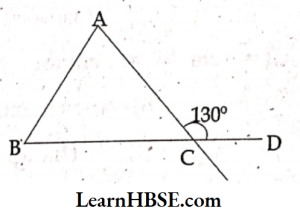
54. An exterior angle of a triangle is of measure 115° and one of its interior opposite angle is 50°. Then the measure of the other interior angle is

1. 165°
2. 65°
3. 155°
4. 45°

Answer: 2

55. Two angles of a triangle are 50°, 60° then the third angle is ( )

1. 10°
2. 55°
3. 70°
4. 110°

Answer: 3

Fill in the blanks:

56. In any right-angled triangle,…………is the longest side.

Answer: hypotenuse

57. The total measure of the three angles of a triangle is……………..

Answer: 180°

58…………is a simple closed figure made of three line segments.

Answer: Triangle

59. If the Pythagoras property holds, the triangle must be……..

Answer: right-angled

60. A ABC is right angled at C. If AC = 5 cm and BC = 12 cm then the length of AB =

Answer: 13 cm

61. Match the following:

1. 7 cm, 7 cm, 7 cm     (  ) A) Scalene triangle

2. 4 cm, 5 cm, 6 cm     (  ) B) Obtuse- angled triangle

3. 6 cm, 6 cm, 8 cm     (  ) C) Right – angled triangle

4. 30°, 60°, 90°             (  ) D) Equilateral triangle

5. 30°; 50°, 100°           (  ) E) Isosceles triangle

Answer:

1. D . 2. A 3. E 4. C 5. B