Haryana Board Class 7 Maths Solutions For Chapter 7 Comparing Quantities
1. Introduction: In our daily life, there are many occasions when we compare two quantities.
Example:
- Heena is 150 cm toll; Amir is 75 cm tall.
- Heena is two times taller than Amir.
- Amir’s height is 1/2 of Heena’s.
- Speed of cheetah is 120 km per hour. Speed of man is 20 km per hour.
- The speed of cheetah is 6 times the speed of man.
- The speed of a man is 1/6 of the speed of a cheetah.
In example: 1
1. We write the ratio of their heights as Heena’s height: Amir’s height – 150: 75 or 2: 1
In example: 2
2. We write the ratio of their speeds as
Speed of man: Speed of cheetah : 20: 120 or 1: 6
To compare two quantities, the units must be the same.
2. Ratio :
We compare two quantities of some kind by division. We use Y this symbol to express the ratio.
For any non-zero numbers a and b, a is to b is a ratio.
a/b is written as a: b.
‘a’ is known as the first term or antecedent.
‘b’ is known as the second term or consequent.
3. Equivalent ratio:
A ratio does not change if its first and second terms are multiplied or divided by the same non-zero number.
Example: 15: 25 (Multiplying by 2)
15X2: 25×2=30: 50
15:25 (Dividing by 5)
15 +5: 25 +5 = 3:5
HBSE Class 7 Comparing Quantities Solutions
4. Ratio in the Simplest Form:
A ratio a: b is said to be in the simplest form if its antecedent ‘a’ and consequent ‘b’ have no common factors except 1. A ratio in the simplest
form is also called the ratio in the lowest terms.
Example: 24: 72
24: 72=\frac{24}{72}=\frac{1}{3}=1: 3
5. Comparison of ratios:
Steps :
- Write each of the ratios in the form of a fraction in the simplest form.
- Find the LCM ofdenominators of the two fractions.
- Make each of the fractions its respective equivalent fractions in such way that the denominators should be equal to the LCM.
- Compare the numerators of each of the equivalent fractions. The fraction having the larger numerator will be larger than the other.
Example:
In 5: 6; 6:7 which is bigger ?
Solution:
\( 5: 6=\frac{5}{6}: 6: 7=\frac{6}{7} \)LCM of 6 and 7 is 6×7=42
\( \frac{5}{6}=\frac{5 \times 7}{6 \times 7}=\frac{35}{42} ; \frac{6}{7}=\frac{6 \times 6}{7 \times 6}=\frac{36}{42} \) \( \text { In } \frac{35}{42}, \frac{36}{42} \text { the bigger fraction is } \frac{36}{42} \)The ratio 6: 7 is bigger than 5: 6.
6. Proportion:
The ratios which are equivalent are said to be in proportion.
Four numbers a, b, c, d are in proportion ad=bc
Product ofmeans = Product of extremes;
Proportions are also used in the making of National flags
7. Unitary method:
The method offinding the value ofone article first from the value of the given number of articles and then the value of the required number of articles is called the unitary method.
Example: 6 bowls cost Rs. 90/-. What would be the cost of 10 such bowls ?
Solution:
Cost of 6 bowls = Rs. 90
Cost of 1 bowl = Rs \( \frac{90}{6} \)
Hence the cost of 10 bowls = Rs.\( \frac{90}{6} \times 10\)
= Rs. 15X10 = Rs. 150
Ratios also appear in the form of percentages.
We use percentages to express profit, loss,discount and interest.
Expressing them in percentages makes comparisons easy.
\( \begin{aligned}& \text { gain/loss } \%=\frac{\text { gain } / l o s s ~}{\times 100} \\
& \text { Cost price } \\
& \text { Discount } \%=\frac{\text { Discount } \times 100}{\text { Marked price }}
\end{aligned} \)
The money borrowed or lent outfor a certain period is called the Principal. This money would be used by the borrowerfor some time before it is returned. For keeping this money for some time the borrower has to pay some extra money to the bank. This is known as Interest.
The amount that is to be repayed back is equal to the sum of the borrowed principal and the interest
That is Amount = Principal + Interest.
Interest is generally expressed as percent of the principal for a period of one year. It is written as say 10% peryear orper annum or in short as 10% p.a
Haryana Board Class 7 Maths Comparing Quantities solutions
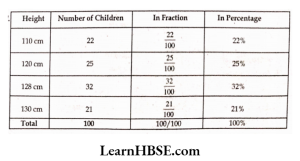
1. Find the percentage of children of different heights for the following data.
Solution:
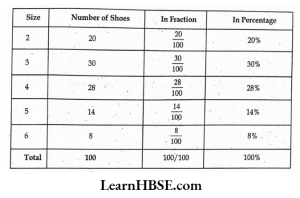
2. A shop has the following number of shoe pairs of different sizes.
Size 2: 20; Size 3: 30; Size 4: 28; Size 5: 14; Size 6: 8
Write this information in tabular form as done earlier and find the Percentage of each shoe size available in the shop
Solution:
1. A collection of 10 chips with different colours is given.

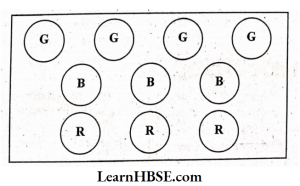
Fill the table and find the percentage of chips of each colour
Solution:

Key Questions in Comparing Quantities for Class 7 HBSE
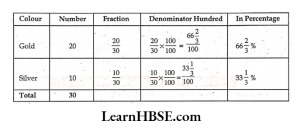
2. Mala has a collection of bangles. She has 20 gold bangles and10 silver bangles. What is the percentage of bangles of each type? Can you put it in the tabular form as donein the above example?
Solution:
1. Look at the examples below and in each of them, discuss which is better for comparison. In the atmosphere,1 g of air contains:
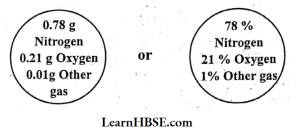
Solution: In the atmosphere the quantity of air contained in percent is better for comparison at a glance..
The second one is better for comparison.
2. A shirt has:
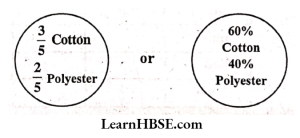
Solution:
Quantity of blending of cotton and polysterin a shirtis easy to understand in terms of percentage.
The second oneisbetter for comparison
1) Can you eat 50% of a cake ? Can you eat 100% of a cake ? Can you eat 150% of a cake ?
Solution:
Yes, we can eat 50% of a cake.
Yes, we can eat 100% of a cake.
No, we cannot eat 150% of a cake.
2) Can a price of an item go up by 50% ?
Can a price of an item go up by 100% ?
Can a price of an item go up by 150% ?
Solution:
Yes, theprice of anitemcan goupby 50%.
Yes, the price of an item can go up by 100%.
Yes, the price of an item can go up by 150%.
1. Convert the following to percents:
\( \frac{12}{16} \)
3.5
\( \frac{49}{50} \)
\( \frac{2}{2} \)
0.05
Solution:
1) \( \frac{12}{16}=\frac{12}{16} \times 100=75 \% \)
2) 3.5 = 3.5×100
\( =\frac{35}{10} \times 100=350 \% \)3) \( \frac{49}{50}=\frac{49}{50} \times 100=98 \% \)
4) \( \frac{2}{2}=\frac{2}{2} \times 100=1 \times 100=100 \% \)
5) 0.05 = 0.05 x 100
\( =\frac{5}{100} \times 100=5 \% \)2.1) Out of 32 students, 8 are absent. What present of the students are absent?
Solution:
Out of 32 students 8 are absent. Writing
this as a fraction we get \( \frac{8}{32} \).
\( \frac{8}{32} \times 100=25 \)25% students are absent.
How to calculate percentage Class 7 HBSE
2) There are 25 radios, 16 of them are put of order. What percent of radios are out of order?
Solution:
Total number of radios = 25
Number of radios which are out of order = 16
Writing this as a fraction we get
\( \frac{16}{25} \) \( \frac{16}{25}=\frac{16}{25} \times 100=64 \% \)64% of radios are out of order.
3) A shop has 500 items, out of which 5 are defective. What percent are defective ?
Solution:
Total number of items = 500
Number of items defective = 5
Writing this as a fraction = \( \frac{5}{500} \)
l% of items are defective
Practice Problems Comparing Quantities Class 7 Haryana Board
4) There are 120 voters, 90ofthem voted yes. What percent voted yes ?
Solution:
Total number of voters = 120
Numbers of voters voted yes = 90
Writing this as a fraction = \( \frac{90}{120} \)
\( \frac{90}{120}=\frac{90}{120} \times 100 \%=75 \% \)75% voters voted yes.
Look at the table, observe, and complete it:
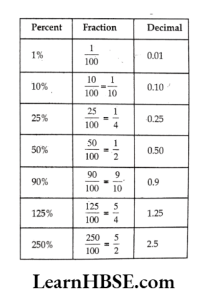
1. 35% +________% = 100%;
64% + 20% +____________% = 100%
45% = 100% -____________%;
70% = _____________%-30%
Solution:
35% + 65% = 100%;
64% + 20% + 16% = 100%
45% = 100% -55%;
70% =100% -30%
2. If 65% of students in a class have a bicycle, what percent of the students do not have bicycles ?
Solution:
Number of students having bicycle in a class = 65%
Out of 100 students 65 of them have a bicycle.
Number of students do not have a bicycle = 100% – 65%. = 35%.
35% of students do not have a bicycle.
3. We have a basket full of apples, oranges and mangoes.If 50% are apples, 30% are oranges, then whatpercent are mangoes?
Solution:
Out of 1,00 given fruits, apples are 50,oranges are 30 and the remaining are mangoes.
Percentage of mangoes
= 100% -50% -30%
= 100%’-80% =20%
Consider the expenditure made on a dress. 20% on embroidery, 50%pn cloth, 30% on stitching. Can you think of more such examples ?
Solution:
Yes, some more examples are as follows:
1) Maths examination was conducted for 100 marks and was observed that 35% of the students,got marks below 50. 29% of the students gotmarks between 60
and 75. 46% of the students gotmarks above 80%.
2) An alloy is made of following compositions :
Copper: 35%; Nickel: 40%; Zinc: 25%
What percent of these figures are shaded?
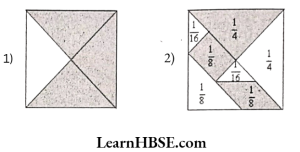
You can make some more figures yourself and ask your friends to estimate the shaded parts.
Solution:
1) Fractions which are,shaded
\( =\frac{1}{4}+\frac{1}{4}+\frac{1}{4}=\frac{3}{4} \)Shaded triangular partin the fraction
\( =\frac{3}{4} \)Percentage of shaded triangular part
\( =\frac{3}{4} \times 100 \%=75 \% \)2) Fraction of tangram which is shaded
\( =\frac{1}{4}+\frac{1}{8}+\frac{1}{8}=\frac{2+1+1}{8}=\frac{4}{8}=\frac{1}{2} \)Percentage of total shaded parts
\( =\frac{1}{2} \times 100 \%=50 \% \)1. Find
1) 50% of 164
Solution: 50% of 164
\( =\frac{50}{100} \times 164=82 \)2) 75% of 12
Solution: 75% of 12
\( =\frac{75}{100} \times 12=9 \)3) \( 12 \frac{1}{2} \% \text { of } 64 \)
Solution:
\( \begin{aligned}& 12 \frac{1}{2} \% \text { of } 64 \\
& \frac{25}{2} \% \text { of } 64=\frac{25}{2} \times \frac{1}{100} \times 64=8
\end{aligned} \)
2. 8% children of a class of 25 like getting wet in the rain. How many children like getting wet in the rain ?
Solution.
Children who like getting wet in the rain = 8% of 25
\( =\frac{8}{100} \times 25=2 \)1. 9 is 25% of what number ?
Solution:
Let the required number be P
25% of P = 9
\( \begin{aligned}& \frac{25}{100} \times P=9 \\
& \frac{P}{4}=9
\end{aligned} \)
P= 9 x 4 = 36
Required number is 36
Important Concepts Comparing Quantities Class 7 HBSE
2. 75% at what number is 15?
Salution:
let the number be P
75% of P=15
\( \begin{aligned}& \frac{75}{100} \times P=15 \\
& \frac{3 P}{4}=15 \\
& P=15 \times \frac{4}{3}=20
\end{aligned} \)
Required number is 20
Haryana Board Class 7 Maths Solutions For Chapter 7 Exercise-7.1
1. Convert the given fractional numbers to percents.
1) \( \frac{1}{8} \)
Solution:
\( \begin{aligned}& \frac{1}{8}=\frac{1}{8} \times 100 \% \\
& =\frac{25}{2} \%=12.5 \%
\end{aligned} \)
2. \( \frac{5}{4} \)
Solution:
\( \frac{5}{4}=\frac{5}{4} \times 100 \%=\frac{500}{4} \% \)= 125%
Profit and loss formula Class 7 Haryana Board
3. \( \frac{3}{40} \)
Solution:
\( \begin{aligned}& \frac{3}{40}=\frac{3}{40} \times 100 \% \\
& =\frac{15}{2} \%=7.5 \%
\end{aligned} \)
4. \( \frac{2}{7} \)
Solution:
\( \begin{aligned}& \frac{2}{7}=\frac{2}{7} \times 100 \% \\
& =\frac{200}{7} \%=28 \frac{4}{7} \%
\end{aligned} \)
2. Convert the given decimal fractions to percents
1) 0.65
Solution:
\( \begin{aligned}0.65 & =\frac{65}{100} \\
& =\frac{65}{100} \times 100 \% \\
& =65 \%
\end{aligned} \)
2) 2.1
Solution:
\( \begin{aligned}2.1 & =\frac{21}{10} \\
& =\frac{21}{10} \times 100 \% \\
& =210 \%
\end{aligned} \)
3) 0.02
Solution:
\( \begin{aligned}0.02 & =\frac{2}{100} \\
& =\frac{2}{100} \times 100 \% \\
& =2 \%
\end{aligned} \)
4) 12.35
Solution:
\( \begin{aligned}12.35 & =\frac{1235}{100} \\
& =\frac{1235}{100} \times 100 \% \\
& =1235 \%
\end{aligned} \)
HBSE Class 7 Maths Chapter 7 Guide Comparing Quantities
3. Estimate what part of the figures are coloured and hence find the percent which is coloured.
Solution:
1) \( \begin{aligned}
&\frac{1}{4} \text { part is coloured }\\
&\frac{1}{4}=\frac{1}{4} \times 100 \%=25 \%
\end{aligned} \)
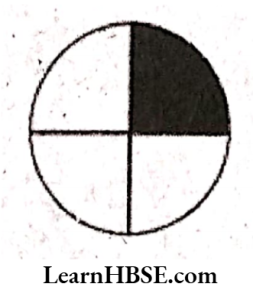
2) \( \begin{aligned}
&\frac{3}{5} \text { part is coloured }\\
&\frac{3}{5}=\frac{3}{5} \times 100 \%=60 \%
\end{aligned} \)

3)
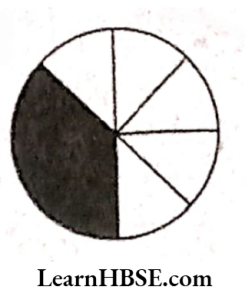
& \frac{3}{8} \text { part is coloured } \\
& \frac{3}{8}=\frac{3}{8} \times 100 \% \\
& \quad=\frac{75}{2} \%=37.5 \%
\end{aligned} \)
4. Find:
1) 15% of 250
Solution: 15% of 250
\( \begin{aligned}&=\frac{15}{100} \times 250\\
&=\frac{75}{2}=37.5
\end{aligned} \)
2) 1% of 1 hour
Solution:
1% of 1 hour
\( \begin{aligned}& =\frac{1}{100} \times 1 \text { hour }=\frac{1}{100} \text { hour } \\
& =\frac{1}{100} \times 60=\frac{3}{5} \text { minute } \\
& =\frac{3}{5} \times 60=36 \mathrm{sec}
\end{aligned} \)
3) 20% of Rs. 2500
Solution:
20% of 2500 \( =\frac{20}{100} \times \text { Rs. } 2500 \)
= Rs. 500
4) 75% of 1 kg
Solution:
75% of 1 kg.
\( \begin{aligned}& =\frac{75}{100} \times 1 \mathrm{~kg}=\frac{3}{4} \mathrm{~kg} \\
& =\frac{3}{4} \times 1000=750 \mathrm{grams}
\end{aligned} \)
5. Find the whole quantity if
1) 5% of it is 600
Solution:
Let the whole quantity be P
5% of P is 600
\( \begin{aligned}&\frac{5}{100} \times P=600\\
&\frac{P}{20}=600
\end{aligned} \)
P = 600 x 20 = 12000
The whole quantity is 12000.
2) 12% of it is Rs. 1080.
Solution:
Let the whole quantity he Rs. P
12% of Rs. P = Rs. 1060
\( \begin{aligned}& \frac{12}{100} \times P=1080 \\
& \frac{3 P}{25}=1080
\end{aligned} \)
3P = 1060 x 25
\( P=\frac{1080 \times 25}{3}=\text { Rs. } 9000 \)The whole quantity is Rs. 9000.
3) 40% of it is 500 km.
Solution:
Let the whole quantity be P km 40% of P km = 500 km
\( \frac{40}{100} \times P=500 \) \( \frac{2 P}{5}=500 \)2P = 500 x 5
\( P=\frac{500 \times 5}{2}=1250 \mathrm{~km} \)The whole quantity is 1230 km
4) 70% of it is 14 minutes
Solution:
Let the whole quantity be P minutes
70% of P minutes = 14 minutes
\( \begin{aligned}& \frac{70}{100} \times P=14 \\
& \frac{7 \mathrm{P}}{10}=14
\end{aligned} \)
7P =14 x 10
\( P=\frac{14 \times 10}{7}=20 \)The whole quantity is 20 minutes
3) 8% of it is 40 litres.
Solution:
let the whole quantity be P litres.
8% of P litres = 40 litres
\( \begin{aligned}& \frac{8}{100} \times P=40 \\
& \frac{2 P}{25}=40 \\
& 2 P=40 \times 25 \\
& P=\frac{40 \times 25}{2}=500
\end{aligned} \)
The whole quantity is 500 litres
6. Convert given percents to decimal fractions and also to fractions in simplest forms:
1) 25%
Solution:
\( \begin{aligned}& 25 \%=\frac{25}{100}=0.25 \\
& 25 \%=\frac{25}{100}=\frac{1}{4}
\end{aligned} \)
2) 150%
Solution:
\( \begin{aligned}& 150 \%=\frac{150}{100}=1.50 \\
& 150 \%=\frac{150}{100}=\frac{15}{10}=\frac{3}{2}
\end{aligned} \)
3) 20%
Solution:
\( \begin{aligned}& 20 \%=\frac{20}{100}=0.20 \\
& 20 \%=\frac{20}{100}=\frac{1}{5}
\end{aligned} \)
4) 5%
Solution:
\( \begin{aligned}& 5 \%=\frac{5}{100}=0.05 \\
& 5 \%=\frac{5}{100}=\frac{1}{20}
\end{aligned} \)
Ratio and Proportion Class 7 Haryana Board
7. In a city, 30% are females, 40% are males and remaining are children. What percent are children?
Solution:
Total population of the city = 100%
Females – 30%
Males = 40%
Children = 100- (30 + 40)
=100-70 = 30%
8. Out of 15,000 voters in a constituency,60% voted. Find the percentage of voters who didnot vote. Can you now find how many actually didnot vote ?
Solution:
Number of voters in the constituency = 15,000
Voters who voted = 60%
Voters who did not vote = 100% -60% = 40%.
Actual number of voters who did not vote = 40% of 15,000
\( =\frac{40}{100} \times 15000=40 \times 150=6000 \text { voters } \)9. Meeta saves Rs. 4000 from her salary.If this is 10% of her salary. What is her salary?
Solution: Let the salary of Meeta be Rs. P
Given Rs 4000 is 10% of her salary
10% of P = 4000
\( \begin{aligned}& \frac{10}{100} \times P=4000 \\
& \frac{P}{10}=4000
\end{aligned} \)
P = 4000x 10 = 40000
The salary of Meetais Rs. 4000.
10. A local cricket team played 20 matches in one season.It won 25% of them. How many matches did they win?
Solution:
Let the total number of matches won be P.
Given 25% of matches were won.
25% of 20 = P
\( \frac{25}{100} \times 20=P \Rightarrow 5=P \)Number of matches won by the team = 5
Solutions To Try These
1. Divide 15 sweets between Manu and Sonu so that they get 20% and 80% of them respectively.
Solution: Total number of sweets = 15
No. of sweets Manu gets = 20% of 15
\( =\frac{20}{100} \times 15=3 \)No. of sweets Sonu gets = 80% of15
\( =\frac{80}{100} \times 15=12 \)2. If angles of a triangle are in the ratio.2:3:4. Find the value of each angle.
Solution:
Angles of a triangle are in the ratio 2:3:4
Total of the parts = 2 + 3 + 4 = 9
Sum of the measures of the three angles of a triangle = 180°
\( \begin{aligned}& \text { First angle }=\frac{2}{9} \times 180^{\circ}=40^{\circ} \\
& \text { Second angle }=\frac{3}{9} \times 180^{\circ}=60^{\circ} \\
& \text { Third angle }=\frac{4}{9} \times 180^{\circ}=80^{\circ}
\end{aligned} \)
The value of each angle = 40°, 60°, 80°
Solutions To Try These
1. Find percentage of increase or decrease:
1) Price of shirt decreased from Rs. 280 to Rs. 210.
Solution:
Decreased price of shirt- Rs. 280-Rs. 210
=Rs. 70
Percent decrease
\( \begin{aligned}& =\frac{\text { Amount of decrease }}{\text { Original price }} \times 100 \% \\
& =\frac{70}{280} \times 100 \%=25 \%
\end{aligned} \)
2) Marks in a test increased from 20 to 30.
Solution:
Increased marks- 30 – 20 = 10
Percent increase
\( \begin{aligned}& =\frac{\text { Increased marks }}{\text { Original marks }} \times 100 \% \\
& =\frac{10}{20} \times 100 \%=50 \%
\end{aligned} \)
HBSE 7th Class Comparing Quantities Word Problems
2. My mother says, in her childhood petrol was Rs.1 a litre.It is Rs. 52 per litre today.By what percentage has the prife gone up?
Solution:
Cost of 1 litre petrol in her childhood = Rs.1
Cost of 1 litre petrol today is = Rs. 52
Increase,in the price of 1 litre petrol = Rs. 52 – Rs. 1 = Rs. 51
Percentage of price increase
\( \begin{aligned}& =\frac{\text { Amount increase }}{\text { Original cost }} \times 100 \% \\
& =\frac{51}{1} \times 100 \%=5100 \%
\end{aligned} \)
Solutions To Try These
1. A shopkeeper bought a chair for Rs. 375 and sold it for Rs 400. Find the gain percentage
Solution: C.P. of a chair = Rs. 375
S.P. of a chair = Rs. 400
SP>CP
Gain = S.P. – C.P
= Rs. 400 – Rs. 375- Rs. 25
= \( \begin{aligned}
& \frac{\text { Gain }}{\text { C.P. }} \times 100 \% \\
& \quad=\frac{25}{375} \times 100 \% \\
& =\frac{20}{3} \%=6 \frac{2}{3} \%
\end{aligned} \)
2. Cost of an item is Rs. 50.It was sold with a profit of 12%. Find the selling price.
Solution:
Cost price of an item Rs. 50
Gain = 12% of Rs. 50
\( =\frac{12}{100} \times 50=\text { Rs. } 6 \)S.P.= C.P. + Gain = Rs. 50 + Rs. 6 = Rs. 56
The selling price of the item Rs. 56
3. An article was sold for Rs 250 with a profit of 5%. What was its cost price?
Solution:
Selling price of an article = Rs. 250
Gain = 5% of C.P.
\( \begin{aligned}& =\frac{5}{100} \times \text { C.P. } \\
& =\frac{1}{20} \text { C.P. }
\end{aligned} \)
S.P. = C.P. + Gain
\( 250=\text { C.P. }+\frac{1}{20} \text { C.P. } \) \( \begin{aligned}& 250=\text { C.P. }\left(1+\frac{1}{20}\right) \\
& 250=\text { C.P. } \times \frac{21}{20} \\
& \text { C.P. }=\frac{250 \times 20}{21}=\frac{5000}{21}=\text { Rs. } 238 \frac{2}{21}
\end{aligned} \)
The cost price of the article
\( =\text { Rs. } 238 \frac{2}{21} \)4. An item was sold for Rs. 540 at a loss of 5%. What was its cost price?
Solution:
Selling price of an item = Rs. 540
Loss = 5%
Actual loss =5% of C.P
\( =\frac{5}{100} \times C . P .=\frac{1}{20} \text { C.P. } \)S.P. = CP- Loss
\( \begin{aligned}& 540=C P-\frac{1}{20} C . P . \\
& 540=C P\left(1-\frac{1}{20}\right) \\
& 540=C P \times \frac{19}{20}
\end{aligned} \) \( C P=540 \times \frac{20}{19}=\frac{10800}{19} \) \( C P=\text { Rs. } 568 \frac{8}{19} \)
The cost price of the item
\( =\text { Rs. } 568 \frac{8}{19} \)Solutions To Try These
1. Rs. 10,000 is invested at 5% interest rate p.a. Find the interest at the end of one year.
Solution:
Principal (P) = Rs. 10,000
Rate of interest (R) = 5%
Interest at the end of one year \( I=\frac{P R T}{100} \)
\( =\frac{10.000 \times 5 \times 1}{100}=\text { Rs. } 500 \)Interest at the end of one year = Rs.500
Sample Problems Comparing Quantities Haryana Board Class 7
2. Rs. 3,500 is given at 7%. p.a. rate of interest. Find the interest which will be received at the end of two years.
Solution:
Principal (P) = Rs. 3,500
Rate of interest (R) = 7%
Time (T) = 2 years
Interest at the end of two years
\( \begin{aligned}I & =\frac{P \times R \times T}{100} \\
& =\frac{3500 \times 7 \times 2}{100}=\text { Rs. } 490
\end{aligned} \)
Interest at the end of two years is Rs. 490
3. Rs. 6,050 is borrowed at 6.5% rate of interest p.a. Find the interest and the amount to be paid at the end of 3 years.
Solution:
Principal (P) = Rs, 6,050
Rate of interest (R) =6.5%
Time (T) =3 years
Interest at the end of 3 years
\( \begin{aligned}& I=\frac{P \times R \times T}{100}=\frac{6050 \times 6.5 \times 3}{100} \\
& =\frac{6050 \times 65 \times 3}{100 \times 10}=\frac{1179750}{1000}
\end{aligned} \)
= Rs. 1179.75
Amount (A) = Principal + Interest
Amount to be paid at tire end of 3 yearsis
= Rs. 6050 + Rs. 1179.75
= Rs. 7229.75
4. Rs. 7,000 is borrowed at 3.5% rate of interest p.a. borrowed for 2 years. Find the amount to be paid at the end of the second year.
Solution:
Principal (P) = Rs. 7,000
Rate of Interest (R) = 3.5%
Time (T) = 2 years
Interest to be paid at the end of second year
\( \begin{aligned}& I=\frac{P \times R \times T}{100} \\
& =\frac{7000 \times 3.5 \times 2}{100}=\text { Rs. } 490
\end{aligned} \)
Amount (A) = Principal + Interest
Amount to be paid at the end of the second year is = Rs. 7000 + Rs. 490 = Rs. 7490
Solutions To Try These
1. You have Rs. 2400 in your account and the interest rate is 5% After how many years would you earn Rs. 240 as interest.
Solution:
Principal (P) = Rs. 2,400
Rate of interest (R) = 5%
Interest (I) = Rs. 240
Time (T) =?
\( \begin{aligned}& \text { Interest } \mathrm{I}=\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100} \\
& 240=\frac{2400 \times 5 \times \mathrm{T}}{100} \\
& 240=24 \times 5 \times \mathrm{T} \\
& \mathrm{~T}=\frac{240}{24 \times 5}=2
\end{aligned} \)
After 2 years you would earn Rs. 240 as interest.
2. On a certain sum the interest paid after 3 years is Rs. 450 at 5% rate of interest per annum. Find the sum
Solution:
Let the sum be Rs. P
Rate of interest (R) = 5%
Time (T) = 3 years
Interest (I) = Rs. 450
\( I=\frac{P \times R \times T}{100} \) \( 450=\frac{P \times 5 \times 3}{100} \) \( P=\frac{450 \times 100}{5 \times 3}=\text { Rs. } 3000 \)The required sum = Rs. 3000
Haryana Board Class 7 Maths Solutions For Chapter 7 Exercise-7.2
1. Tell what is the profit or loss in the following transactions. Also find profit percent (or) loss per centin each case.
1) Gardening shears bought forRs. 250 and sold for Rs. 325.
Solution:
CP of gardening shears = Rs. 250
SP of gardening shears = Rs. 325
SP>CP
Profit = SP- CP = Rs. 325- Rs. 250
= Rs.75
\( \begin{aligned}\text { Profit \% } & =\frac{\text { Profit }}{C P} \times 100 \% \\
& =\frac{75}{250} \times 100 \%=30 \%
\end{aligned} \)
2) A refrigerator bought for Rs. 12,000 and sold at Rs. 13,500
Solution: CP of refrigerator = Rs. 12,000.
SP of refrigerator = Rs. 13,500
SP>CP
Profit = SP- CP
= Rs. 13,500- Rs. 12,000 = Rs. 1,500
\( \begin{aligned}& \text { Profit } \%=\frac{\text { Profit }}{\text { CP }} \times 100 \% \\
& =\frac{1500}{12000} \times 100 \%=12.5 \%
\end{aligned} \)
3) A cupboard bought for Rs. 2500 and sold at Rs. 3,000
Solution:
CP of cupboard = Rs. 2,500
SP of cupboard = Rs. 3,000
SP>CP
Profit = SP- CP
= Rs. 3000- Rs. 2500
= Rs. 500
\( \begin{aligned}& \text { Profit } \%=\frac{\text { Profit }}{C P} \times 100 \% \\
& =\frac{500}{2500} \times 100 \%=20 \%
\end{aligned} \)
Word problems on profit and loss Class 7 HBSE Maths
4) A skirt bought for Rs. 250 and sold at Rs. 150.
Solution:
CP of skirt = Rs. 250.
SP of a skirt = Rs. 150
CP>SP
Loss = CP- SP
= Rs. 250- Rs. 150
= Rs. 100
\( \begin{aligned}& \text { Loss % }=\frac{\text { Loss }}{\text { CP }} \times 100 \% \\
= & \frac{100}{250} \times 100 \%=40 \%
\end{aligned} \)
2. Convert each part of the ratio to percentage:
1) 3:1
Solution: Given ratio 3:1
Total parts =3 +1=4
Percentage of first part
\( =\frac{3}{4} \times 100 \%=75 \% \)Percentage of second part
\( =\frac{1}{4} \times 100 \%=25 \% \)2) 2:3:5
Solution:
Given ratio = 2:3:5
Total parts = 2 + 3 + 5 = 10
Percentage of first part
\( =\frac{2}{10} \times 100 \%=20 \% \)Percentage of second part
\( =\frac{3}{10} \times 100 \%=30 \% \)Percentage of third part
\( =\frac{5}{10} \times 100 \%=50 \% \)3) 1:4
Solution:
Given ratio 1:4
Total parts =1+4 = 5
Percentage of first part
\( =\frac{1}{5} \times 100 \%=20 \% \)Percentage of second part
\( =\frac{4}{5} \times 100 \%=80 \% \)4) 1:2:5
Solution: Given ratio 1:2:5
Total parts =l+2+5=8
Percentage of firstpart
\( =\frac{1}{8} \times 100 \%=\frac{25}{2} \%=12.5 \% \)Percentage of second part
\( =\frac{2}{8} \times 100 \%=25 \% \)Percentage of third part
\( =\frac{5}{8} \times 100 \%=\frac{125}{2} \% \)= 62.5%
3. The population of a city decreased from 25,000 to 24,500. Find the percentage of decrease.
Solution:
Population at the begining = 25,000
Population after = 24,500
Actual decrease = 500
Percent decrease =
\( \begin{aligned}& \frac{\text { changein population }}{\text { population at the begining }} \times 100 \% \\
& \quad=\frac{500}{25000} \times 100 \%=2 \%
\end{aligned} \)
4. Arun bought a car for Rs. 3,50,000 The next year, theprice wentupto Rs. 3,70,000. What was the percentage of price increase?
Solution:
Price of the carin the first year = Rs. 3,50,000
Price of the carin the next year = Rs. 3,70,000
Increased price of the car
= Rs. 3,70,000 -Rs. 3,50,000
= Rs. 20,000
Percent increase
\( \begin{array}{r}=\frac{\text { Increased price }}{\text { Pricein the first year }} \times 100 \% \\
=\frac{20,000}{3,50,000} \times 100 \%=\frac{40}{7} \%=5 \frac{5}{7} \%
\end{array} \)
5. I buy a TV for Rs. 10,000 and sell it at a profit of 20%. How much money do I get for it ?
Solution:
C.P. of a TV= Rs. 10,000
Profit = 20% of C.P
\( =\frac{20}{100} \times 10,000=\text { Rs. } 2000 \)SP of TV = CP +’Profit
= Rs. 10,000 + Rs. 2,000
= Rs. 12,000
I will get Rs. 12,000 for it.
6. Juhi sells a washing machine for Rs. 13,500. She loses 20% in the bargain. What was the price at which she bought it?
Solution: SP of washing machine = Rs. 13,500
Loss =20% of CP
Now SP = CP- Loss
13,500 = CP -20% of CP
& 13,500=C P-\frac{20}{100} C P \\
& 13,500=C P-\frac{1}{5} C P \\
& 13,500=C P\left(1-\frac{1}{5}\right) \\
& 13,500=\frac{4}{5} C P \\
& \frac{13,500 \times 5}{4}=C P
\end{aligned} \)
CP =3375 X 5 = Rs. 16,875
Juhi bought the washing machine at Rs. 16,875
7.
1) Chalk contains calcium, carbon and oxygen in the ratio10:3: 12. Find the percentage of carbon in chalk.
Solution:
Given ratio =10:3:12
Total parts = 10 + 3 + 12 = 25
Percent of carbon = \( \frac{3}{25} \times 100 \%=12 \% \)
2) If in a stick of chalk,carbon is 3 g, what is the weight of the chalk stick?
Solution:
Let the weight of the chalk stick be
P grams.
12% of P = 3g
\( \frac{12}{100} \times P=3 \) \( P=\frac{3 \times 100}{12}=25 \mathrm{~g} \)The weight of the chalk stick = 25 g
8. Amina buys a book for Rs. 275 and sells it at a loss of 15%. How much does she sell it for ?
Solution:
CP of book = Rs. 275
Loss = 15% of CP
\( \begin{aligned}& =\frac{15}{100} \times 275 \\
& =\frac{4125}{100}=\text { Rs. } 41.25
\end{aligned} \)
SP of the book = CP – Loss
= Rs. 275 -Rs. 41.25
= Rs. 233.75
Amina sells the book for Rs. 233.75
Percentage Problems Class 7 HBSE
9. Find the amount to be paid at the end of 3 years in each case:
1) Principal = Rs. 1,200 at 12% p.a.
Solution:
Principal (P) = Rs. 1,200
Rate of interest (R) =12% pa.
Time (T) = 3 years
\( \begin{aligned}& \text { Interest } \mathrm{I}=\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100} \\
& =\frac{1200 \times 12 \times 3}{100}=\text { Rs. } 432
\end{aligned} \)
Amount (A) = P +1
= Rs. 1200 + Rs. 432
= Rs. 1632
Amount to be paid at the end of 3 years, is Rs. 1632.
2) Principal = Rs. 7,500 at 5%pa.
Solution:
Principal (P) = Rs. 7500
Rate of interest (R) = 5% p.a.
Time (T) = 3 years
\( \text { Interest } \mathrm{I}=\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}=\frac{7500 \times 5 \times 3}{100} \)= Rs.1125
Amount(A)= P+I
= Rs. 7300 + Rs 1125
= Rs, 8625
Amount to be paid at the end of 3 years is Rs. 8625.
10. What rate gives Rs. 280 as interest on a sum of Rs. 56,000in 2 years ?
Solution:
Principal (P) = Ps. 56,000
Interest (T) = Rs. 280
Time (T) =2 years
Rate of interest (R) =?
\( \begin{aligned}& I=\frac{P R T}{100} \Rightarrow R=\frac{I \times 100}{P T} \\
& R=\frac{280 \times 100}{56000 \times 2}=\frac{1}{4}=0.25 \%
\end{aligned} \)
The rate of interest is 0.25 percent per annum.
11. If Meena gives an interest of Rs. 45 for one year at 9% rate pa. What is the sum she has borrowed?
Solution:
Let the sum Meena borrowed be Rs. P.
Rate of interest (R) = 9% per annum
Time (T) =1 year
Interest (I) = Rs. 45
\( \begin{aligned}& I=\frac{P \times R \times T}{100} \\
& 45=\frac{P \times 9 \times 1}{100}
\end{aligned} \) \( P=\frac{45 \times 100}{9} \)
= 5 x 100 = Rs. 500
Meena has borrowed a sum of Rs.500
Haryana Board Class 7 Maths Solutions For Chapter 7 Very Short Answer Questions
1. What is meant by ‘ratio’?
Solution:
The comparison of two quantities is known as ratio.
2. Find the ratio of 3 km to 300 m.
Solution:
3 km = 3 X 1000 m = 3000 m
The required ratio = 3 km: 300 m
= 3000:300 =10:1.
3. Write the equivalent ratio of 2: 3
Solution:
\( 2: 3=\frac{2}{3}=\frac{2 \times 2}{3 \times 2}=\frac{4}{6}=4: 6 \)4. What is meant by ‘Unitary method’?
Solution:
The method in which we find the value of one unit first and then the value of the required number of units is known as unitary method.
5. What is a ‘proportion’?
Solution:
If two ratios are equivalent then the four quantities are said to be in proportion.
The ratios 8: 2 and 16: 4 are equivalent.
8, 2, 16, 4 arein proportion
6. Find 25% of 40
Solution:
\( 25 \% \text { of } 40=\frac{25}{.100} \times 40=10 \)7. If Manohar pays an.interest of Rs 750 for 2 years on a sum of Rs 4,500 find the rate of interest.
Solution:
Principal (P)=Rs 4500
Interest (I) = Rs 750
Time (T) = 2 years
Rate (R) =?
\( I=\frac{P \times T \times R}{100} \) \( 750=\frac{4500 \times 2 \times \mathrm{R}}{100} \) \( R=\frac{750 \times 100}{4500 \times 2}=\frac{25}{3}=8 \frac{1}{3} \% \)8. Last year the cost of 1000 articles was 5000 /-. This year, it went down to 4000/-. Find the percentage decrease in price.
Solution:
Original cost = 5000/-
Present cost = 4000/-
decreasein cost = 1000
% decrease in price = \( \frac{1000}{5000} \) x 100
= 20 %
9. Out,of 12,000 voters in a constituency, 60% voted. Find the No. of people voted in the constituency?
Solution:
By Question, 60% voted means \( \frac{60}{100} \)
Persons voted =\( \frac{12000×60}{100} \) = 7200
Simple Interest formula examples Class 7 HBSE
10. 40% of a number is 800 then find the number.
Solution:
40% of the number is 800
1 % of the number is \( \frac{800}{40} \)
and 100% (Actual No) = \( \frac{800}{40} \) x 100
= 2000
11. Tamarind was soldlast year at? 75/-perkg. This year it is sold at 125 per kg. Find the percentage increase in price?
Solution:
Percentage increase = \( \frac{\text { dif.in price }}{\text { original price }} \times 100 \)
The increase in tamarind price
= \( \frac{125-75}{75} \) x 100
= \( \frac{50}{75} \) x 100
\( =66 \frac{2}{3} \% \)12. Suppose a person buys an article for 650/- and gains 6% on selling it. Find the selling price?
Solution:
CP = 650
Profit % = 6%
Thus, profit = 6% of 650
= \( \frac{6}{100} \) x 650 = 39
We know that SP = CP + Profit
=650+39=689
Thus, the SP = 689
13. Ajay bought a TV for 15,000 and sold it for 14,100. Find the loss percent.
Solution:
By Question, loss =? (15,000.- 14,100) = 900
% loss = \( \frac{900 \times 100}{C P} \)
\( \frac{900 \times 100}{15000} \)= 6%
14. The marked Price of a book is 225. The publisher allows a discount of 10% onit. Find the selling price of it.
Solution:
MP = 225; discount = 10%
SP (100 down) = \( \frac{100 \text {-discount }}{100} \times \text { M.P } \)
\( \frac{225}{100} \times { 90 } \)= 202.50
15. A dealer allows a discount of 10% and still gains by 10%. Find the marked price of an article which cost him 900.
Solution:
Given CP = 900
gain =10%
SP (100 down) =
\( =\frac{100+\text { gain } \times C . P}{100} \)\(\frac{900}{100} \times { 110 } \) = 990
again, discount = 10%
MP (100 up) = \( \frac{\mathrm{SP} \times 100}{100-\text { discount }} \)
\(\frac{990×100}{90} \) = 1100
16. Find the interest on a sum of? 8250 for 3 years at the rate of 8% per annum.
Solution:
Principal (P) = 8250
Rate of interest (R) = 8%
Interest per 3 years (I)
\( \begin{aligned}& =\mathrm{P} \times \frac{\mathrm{R}}{100} \times \mathrm{T} \\
& =8250 \times \frac{8}{100} \times 3
\end{aligned} \)
17. 3000 is lent out at 9% rate of interest. Find the interest which will be received at the end of 2½ years.
Solution:
Amount (P) = 3000,
Rate of Interest (R) = 9%.
\( \mathrm{T}=2 \frac{1}{2} \mathrm{yr} \) \( I=\frac{P \times R \times T}{100}=3000 \times \frac{9}{100} \times \frac{5}{2} \)= 675
18. A child-friendly bank annnounces a , savings scheme for school children. Theywill give kiddybanks to children. Children have to keep their savings in it and the bank collects all the money once in a year. To encourage children savings, they give 6% interest if the amount exceeds 10,000, and otherwise 5%. Find the interest received by the school if they deposit 9000 for one year.
Solution:
Since the deposit is only 9,000 the children get 5% interest only.
Interest = \( \frac{\text { PTR }}{100}=\frac{9000 \times 1 \times 5}{100} \)
= 450
Haryana Board Class 7 Maths Solutions For Chapter 7 Short Answer Questions
19. Shyam’smonthlyincomeis?10,000.He spends 60% of it on family expenses 10% onmedical expenses, 5% on donations and saves by 25%. Find the
amount he spends on each item.
Solution:
Amount spent on family expenses
= 60% of total income
= 60% of 10000
\( =\frac{60}{100} \times 10000 \) = 6000
Similarly, amount spent on medical expenses
\( =\frac{10}{100} \times 10000 \) = 1000
Amount spent on donations
\( =\frac{5}{100} \times 10000 \) = 500
Amount saved = \( =\frac{25}{100} \times 10000 \) = 2500
20. Ramu sold a plot of land for 2,40,000 gaining 20%. Find the costprice ofplot.
Solution:
Method -1:
SP = 2, 40,000 gain 20%
\( \mathrm{CP}=\frac{\mathrm{SP} \times 100}{100+\operatorname{gain} \%} \)CP (100 up) = \( \frac{2,40,000 x 100}{120} \)
= 2,00,000
Method – 2: Since Ramu gained 20% his CP : SP = 100 : 120
By question 100: 120 = x : 2,40,000
x = \( \frac{2,40,000 x 100}{120} \)
= 2,00,000
21. A shopkeeper gives successive discounts of10% and5% onhis articles. Find the net discount on the whole.
Solution:
Let his MP be 100
by two successive discounts,his SP (100
down) = 100x \( \frac{90}{100} \) x \( \frac{95}{100} \)= \( \frac{171}{2} \)
= 85.50
Net discountis (100- 85.5) = 14.5,%
22. In what time will? 6880 amount to 7224, if simple interest is calculated at 10% per annum?
Solution:
Amount = ? 7224
Principle = ? 6880
S.I = Amount – Principle
= 7224-6880 = 344
R% = 10%
\( \begin{aligned}& \text { Now } I=P \times \frac{R}{100} \times T \\
& 344=6880 \times \frac{10}{100} \times T
\end{aligned} \)
344 x 100 = 6880 x 10 x T
Therefore, T = \( \frac{344×100}{6880×10} \)
= \( \frac{1}{2} \) years
= 6 months
23. What sum will yield an interest of 3927 in 2 years and 4 months at 8% per annum?
Solution:
S.I =3927,
R% = 8%
T = 2 year + 4 months
\( \begin{aligned}& \left(2+\frac{4}{12}\right) \mathrm{Yrs} \\
& \left(2+\frac{1}{3}\right) \mathrm{Yrs}=\frac{7}{3} Y \mathrm{rs}
\end{aligned} \) \( \text { Substituting in } \mathrm{I}=\mathrm{P} \times \frac{\mathrm{R}}{100} \times \mathrm{T} \) \( 3927=\mathrm{P} \times \frac{8}{100} \times \frac{7}{3} \)
3927 x 100 x 3 = P x 8 x 7
Therefore,P =\( \frac{3927x100x3}{8×7} /latex]
Thus, P = 21037.50
Therefore, Principal. = 21037.50
Haryana Board Class 7 Maths Solutions For Chapter 7 Long Answer Questions
24. A shopkeeper bought a TV for 9000 and he sold it for 10,000. Find the profit or loss? calculate percentage.
Solution:
Method-1:
Cost price (CP) of the TV = 9000
Selling price (SP) of the TV = 10,000
As SPis greater than CP, the shopkeeper makes a profit:
Profit (P) = 10000 -9000 = 1000
Thus, when the CP is 9000, the shopkeeper makes a profit of 1000
The ratio of profit and cost price is [latex] \frac{1000}{9000} \)
To find the profit percentage we multiply this ratio with 100%
i.e, \( \frac{1000}{9000} \) x 100%
\( =\frac{100}{9} \%=11 \frac{1}{9} \% \)Method -II:
When the CP is 9000, the profit is 1000 Now, when CP is? 100, let the profit be x.
We know that the CP and profit are directly proportional thus, ratio of profit and the ratio of cost price (CP) will be same in both cases.
Therefore, x: 1000 = 100: 9000
\( \frac{x}{1000}=\frac{100}{9000} \)9000 x x = 1000 x 100
\( \frac{1000 x 100}{9000} \) \( =11 \frac{1}{9} \% \)Thus, the profit % \( =11 \frac{1}{9} \% \)
25. In 4 years ? 6,500 amounts to ? 8840 at a certain rate of interest.In what time will 1600 amount to 1816 at the same rate?
Solution:
Case (1):
P = 6500
T = 4 yrs
A = 8840 such that I = (8840- 6500)
= 2340
we have to find rate %
we know \( \frac{\mathrm{PTR}}{100}=\mathrm{I} \)
\( \frac{6500 \times 4 \times \mathrm{R}}{100}=2340 \)R = \( \frac{2340×100}{6500×4} \) = 9 %
Case (2):
given P = 1600 A =1816
T = ? (such that I=(1816-1600)=216)
R = 9%
Substituting these values in \( \frac{\mathrm{PTR}}{100}=\mathrm{I} \)
we get 1600 x T x \( \frac{9}{100} \) = 216
T = \( \frac{216×100}{1600×9} \) = \( \frac{3}{2} \)
\( =1 \frac{1}{2} \mathrm{yrs} \)Haryana Board Class 7 Maths Solutions For Chapter 7 Multiple Choice Answer Questions
1. Ratio of Rs 20 to Rs 50 is
- 2: 5
- 5: 2
- 2: 3
- 3: 5
Answer: 1
2. Equivalent ratio of 6 : 4 is
- 2:8
- 8:2
- 8:12
- 12:8
Answer: 4
3. Percentages are numerators of fractions with denominator
- 10
- 100
- 1000
- 50
Answer: 2
4. If the cost of 10 cans of juice is Rs 200 then the cost of 6 cans of juice is
- Rs 180
- Rs 160
- Rs 120
- Rs 140
Answer: 3
5. \( \mathrm{I}=\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100} \) in this formula P is called
- Interest
- Amount
- Principal
- Rate of interest
Answer: 3
6.Convert \( \frac{1}{3} \) as percent.
- \( \frac{3}{100} \% \)
- \( \frac{100}{3} \% \)
- \( \frac{50}{3} \% \)
- \( \frac{3}{50} \% \)
Answer: 2
7. Choose the correct matching.
1) 0.2 ( ) a) 75%
2) 0.09 ( ) b) 20%
3) 0.75 ( ) c) 9%
- 1-a,2-b,3-c
- 1-b,2-a,3-c
- 1-a,2-c,3-b
- 1-b,2-c,3-a
Answer: 4
8. If 2: 5 and 6 : x are equal then find fourth proportion.
- 20
- 25
- 15
- 30
Answer: 3
9. lire ratio of two angles is 3: 2 and the larger angle is 60. What is the smaller one ?
- 40
- 50
- 60
- 70
Answer: 1
10. Choose the correct matching
1) % ( ) a) Rate
2) / ( ) b) Proportion
3) :: ( ) c) Percent
- 1- a,2-b,3-c
- 1- c,2-a,3-b
- 1- b,2-a,3-c
- 1- c,2-b,3-a
Answer: 2
11. 72% + 15% + X = 100% => X = ………
- 15%
- 20%
- 18%
- 13%
Answer: 4
12. If x and y arein direct proportion, then which of the following is true ?
- \( \frac{x}{y} \text { is constant } \)
- xy is constant
- \( \frac{1}{x} \text { is constant } \)
- y is constant
Answer: 1
13. If C.P of 12 mangoes is equal to the selling price of 15 mangoes, find the loss percentage.
- 10%
- 20%
- 30%
- 40%
Answer: 2
14. If 25% ofa number is 300 then the number is………..
- 1200
- 1250
- 1300
- 1350
Answer: 1
15. If the cost of 10 pens is Rs. 300/- then the cost of one pen is…………..
- Rs. 30
- Rs. 25
- Rs. 50
- Rs. 17.50
Answer: 1
16. If 3, 8, x and 16 are in proportion. The value of x is…….
- 12
- 4
- 8
- 6
Answer: 4
17. The ratio of 8 books to 20 books.
- 2:5
- 5:2
- 4: 5
- 5: 4
Answer: 1
18. What sum will yield an interest of Rs. 1000/-in 2 years at 5% (in Rs) ?
- 10,000
- 12,000
- 15,000
- 20,000
Answer: 1
19. At what rate will ?10,000 amount to ?16,000in 3 yrs ?
- 10%
- 15%
- 20%
- 25%
Answer: 3
20. An amount becomes double in 5 yrs at some SI rate. Find the rate %.
- 25%
- 20%
- 15%
- 10%
Answer: 2
21.What sum will amount to ? 880in 2 years at 5% SI (in Rs)
- 600
- 660
- 800
- 500
Answer: 3
22. Certain sum amounts to ? 7000in 4 yrs and? 6000 in 2 years, the rate % is
- 10%
- 5%
- \( 12 \frac{1}{2} \% \)
- \( 6 \frac{1}{4} \% \)
Answer: 1
23. If the compound ratio of 5: 8 and 3: 7 is 45: x, then x is
- 128
- 72
- 168
- 105
Answer: 3
24. By selling an article for 1100 which is marked at 1200, discount percent is
- \( 6 \frac{1}{4} \% \)
- \( 12 \frac{1}{2} \% \)
- \( 8 \frac{1}{3} \% \)
- 10%
Answer: 3
25. The 30% of 40% of a number is 69 then the number is
- 557
- 575
- 757
- 775
Answer: 2
26. At what rate per annum will X 6360 yield an interest of 1378 in \( 2 \frac{1}{2} \) years ?
- \( 6 \frac{2}{3} \% \)
- \( 8 \frac{1}{3} \% \)
- \( 8 \frac{2}{3} \% \)
- \( 7 \frac{1}{4} \% \)
Answer: 3
27. Ratio’s of sellingprice and costprice are 4: 5, then percentage is
- 10%
- 20%
- 19%
- 25%
Answer: 2
28. Profit is calculated on
- selling price
- cost price
- marked price
- above allAnswer: 2
29. Discount is calculated on
- marked price
- selling price
- cost price
- none of the above
Answer: 1
30. 21% of 85 =?
- 16.85
- 17.05
- 18.05
- 17.85
Answer: 4
31. If 3: 5 = 4.5: x then x – 5 = ?
- 7.5
- 5
- 4.5
- 2.5
Answer: 4
32. 8% of 400 – 4% of 800 + 1% of 500 = ?
- 10
- 20
- 4
- 5
Answer: 4
33. What is the mean proportion of 25: 20:: 20: 16 ?
- 25
- 20
- 16
- 100
Answer: 2
34. If 25% of a number is 40 then the number is
- 100
- 140
- 160
- none
Answer: 3
35. While doing the problem “whatis the cost of 9 bananasif the cost of a dozen bananas is 20 ?” Write the steps in order.
1) Cost of 9 bananas =\( \frac{20}{12} \times 9 \) = 15
2) Cost of 12 bananas = 20
3) Cost of 1 banana = \( \frac{20}{12} \)
- 1,2,3
- 2,1,3
- 2,3,1
- 1,3,2
Answer: 3
36. 40% of a numberis 800 then find the number.
- 1000
- 2000
- 3000
- 4000
Answer: 2
37. If the price of an item goes up by 100%, then the cost of article will be
- doubled
- tripled
- five times
- eight times
Answer: 1
38. When 35% is expressedin decimalit is equal to
- 0.35
- 0.7
- 0.14
- 0.21
Answer: 1
39. \( \frac{4}{16} \) is equal to……..%
- 30%
- 25%
- 35%
- 40%
Answer: 2
40. Arectangleis enlarged fromits originalposition. Which conceptis usedin this aspect?
- Profit
- Percentage
- Proportion
- Simple interest
Answer: 3
41. Two is 10% of x and 20% of y, what is x-y ?
- 1
- 2
- 5
- 10
Answer: 4
42. The markedprice of a machineis Rs. 18,000.Ifitis sold at 20% discount, there is a loss of 4%. Then its costin Rs. is
- 15,000
- 16,000
- 14,000
- 13,000
Answer: 1
43. A is 20% less than B. At what percent B is more than A?
- 25%
- 20%
- 18%
- 22%
Answer: 1
44. What percentage of numbers from1 to 70 has1 or 9in its unit’s digit ?
- 1%
- 14%
- 20%
- 21%
Answer: 3
45. Rani’s salary is increased from 630 to 700, find the increase percent.
- \( 11 \frac{1}{9} \% \)
- \( 8 \frac{1}{2} \% \)
- \( 13 \frac{2}{9} \% \)
- \( 9 \frac{1}{9} \% \)
Answer: 1
46. 12% of a certain sum of money is 43.5. Find the sum.
- 360
- 362.50
- 340.50
- 352.50
Answer: 2
47. Out of 40 students 5 are absent. What percent of the students are present ?
- \( 12 \frac{1}{2} \% \)
- 40%
- \( 87 \frac{1}{2} \% \)
- 4%
Answer: 3
48. The C.P of 25 articles is equal to the S.P of 20 articles. Whatis the gain% ?
- 0.25%
- 2.5%’
- 25%
- 0.025%
Answer: 3
49. A man buys aradio for ? 500 and sellsit at a gain of 25%. What is the S.P of the radio?
- 600
- 575
- 625
- 675
Answer: 3
50. At what rate of interest per annum will a sum double itselfin 8 years ?
- \( 6 \frac{1}{4} \% \)
- \( 12 \frac{1}{2} \% \)
- \( 11 \frac{1}{2} \% \)
- \( 11 \frac{1}{4} \% \)
Answer: 2
51. Suppose aperson buys an article for? 650 and gains 6% on sellingit. The sellingprice is
- 700
- 650
- 698
- 689
Answer: 4
52. Ramu sold a plot of land for? 24000 gaining 20%. The cost price of the plot is
- 28,000
- 2,800
- 20,000
- 19,200
Answer: 3
53. 3000 is lent out at 9% rate of interest. The interest which will be received at the end of \( 2 \frac{1}{2} \) years is
- 675
- 725
- 756
- 657
Answer: 1
54. At what rate per annum will the principal triples in 16 years ?
- 25%
- 24%
- \( 12 \frac{1}{2} \% \)
- 20%
Answer: 3
55. At what rate per annus will ? 6360 yield an interest of 1378in 2 \( [/2 \frac{1}{2}latex] years.
- [latex] 6 \frac{2}{3} \% \)
- \( 8 \frac{1}{3} \% \)
- \( 8 \frac{2}{3} \% \)
- \( 7 \frac{1}{4} \% \)
Answer: 4
56. What is the decimal form of this figure?

- \( \frac{17}{10} \)
- 0.17
- 0.18
- 1.8
Answer: 3
Fill in the blanks:
57. To compare two quantities the units must be the ………
Answer:
58. 1 Dozen =………..items.
Answer:
59. Percentage is derived from the Latin word…………
Answer:
60. The buying price of any item is known as its …………….
Answer:
61. Amount = ………+………..
Answer:
62. Match the following:
1. Out of 25 children in a class 15 are girls. The percentage of girls is items. ( ) A) 20%
2. Write – as a percent ( ) B) 50%
3. Convert 0.2 as a percent ( ) \( 33 \frac{1}{3} \% \)
4. A school team won 6 games this year against 4 games won last year. Write the percent increase. ( ) D) 0.25%
5. What rate gives Rs 280 as interest on a sum of Rs 56000 in 2 years? ( ) E) 60%
Answer:
1. E 2. C 3. A 4. B 5. D
