Haryana Board Class 7 Maths Solutions For Chapter 8 Rational Numbers
Key Concepts
- 1. Introduction :
- The numbers used for counting objects around us are called Counting numbers (or) Natural numbers They are 1, 2, 3, 4,……,…
- Including ‘0’ to natural numbers we get the whole numbers i.e. 0,1,2,3,4, ………
- The negatives of natural numbers were put together with whole numbers to make up integers. They are……..- 3,-2,-1, 0,1,2,3,……….
- The numbers of the form \( \frac{\text { numerator }}{\text { denominator }} [latex] where the numerator is either 0 or a positive integer and the denominator, a positive integer are called fractions.
Need for rational numbers: We know that integers can be. used to denote opposite situations involving numbers.
- Definition of a rational number:
A rational number is defined as number that can be expressed in the form of [latex] \frac{p}{q} \) where p and q are integers and q ≠ 0.
Example :
\( \frac{4}{5} ; \frac{-3}{4} ; \frac{3}{8} ; 1 \frac{2}{3} \text { etc. } \) \( 0.5=\frac{5}{10} ; 0.333=\frac{333}{1000} \text { etc. } \)1. Is the number \( \frac{2}{-3} \) rational ? Think about it.
Solution: Yes; \( \frac{2}{-3} \) is a rational number.
It is in the form of latex] \frac{p}{q} [/latex], where p = 2; q = -3 both are integers.
2. List ten rational numbers.
Solution:
\( \frac{3}{8}, \frac{2}{3}, \frac{-3}{2}, \frac{4}{-9}, \frac{1}{2}, \frac{3}{4}, \frac{-6}{11}, 2 \frac{3}{5}, \) \( 0.75=\frac{75}{100}, \frac{17}{79} . \)HBSE Class 7 Rational Numbers Solutions
Fill in the boxes:
1)
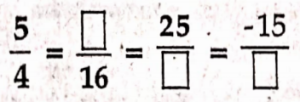
Solution:
\( \begin{aligned}& \frac{5}{4}=\frac{5 \times 4}{4 \times 4}=\frac{20}{16} \\
& \frac{5}{4}=\frac{5 \times 5}{4 \times 5}=\frac{25}{20} \\
& \frac{5}{4}=\frac{5 \times(-3)}{4 \times(-3)}=\frac{-15}{-12} \\
& \frac{5}{4}=\frac{20}{16}=\frac{25}{20}=\frac{-15}{-12}
\end{aligned} \)
2)
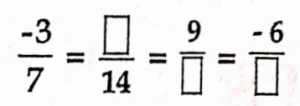
Solution:
\( \begin{aligned}& \frac{-3}{7}=\frac{-3 \times 2}{7 \times 2}=\frac{-6}{14} \\
& \frac{-3}{7}=\frac{-3 \times(-3)}{7 \times(-3)}=\frac{9}{-21} \\
& \frac{-3}{7}=\frac{-3 \times 2}{7 \times 2}=\frac{-6}{14} \\
& \frac{-3}{7}=\frac{-6}{14}=\frac{9}{-21}=\frac{-6}{14}
\end{aligned} \)
Solutions To Try These
1. Is 5 a positive rational number?
Solution:
Yes,5 is a positive rational number. It can be written as \( \frac{5}{1} \) . The numerator is 5 and denominator is 1.
2. List five more positive rational numbers.
Solution:
\( \frac{3}{7}, \frac{5}{12}, \frac{4}{19}, \frac{6}{13}, \frac{17}{9} \)Solutions To Try These
1. Is – 8 a negative rational number?
Solution:
Yes,- 8 is a negative rational number. It can be written as \( \frac{-8}{1} \) . The numerator is a negative integer and the denominator is
a positive integer.
2. List five more negative rational numbers.
Solution:
\( \frac{-4}{9}, \frac{-7}{11}, \frac{-5}{11}, \frac{-15}{22}, \frac{-3}{10} \)Solutions To Try These
Which of these are negative rational numbers?
- \( \frac{-2}{3} \)
- \( \frac{5}{7} \)
- \( \frac{3}{-5} \)
- 0
- \( \frac{6}{11} \)
- \( \frac{-2}{-9} \)
Solution:
1) \( \frac{-2}{3} \) and 3. \( \frac{3}{-5} \) are negative rational numbers.
Solutions To Try These
Find the standard form of
1) \( \frac{-18}{45} \)
Solution: The HCF of 18 and 45 is 9.
\( \frac{-18}{45}=\frac{-18 \div 9}{45 \div 9}=\frac{-2}{5} \)2) \( \frac{-12}{18} \)
Solution: The HCF of 12 and 18 is 6.
\( \frac{-12}{18}=\frac{-12 \div 6}{18 \div 6}=\frac{-2}{3} \)Solutions To Try These
Find five rational numbers between
\( \frac{-5}{7}\) and \( \frac{-3}{8}\).
Solution:
\( \frac{-5}{7}=\frac{-5 \times 8}{7 \times 8}=\frac{-40}{56} \) \( \frac{-3}{8}=\frac{-3 \times 7}{8 \times 7}=\frac{-21}{56} \)\( \frac{-40}{56}<\frac{-39}{56}<\frac{-38}{56}<\frac{-29}{56} \) \( <\frac{-27}{56}<\frac{-22}{56}<\frac{-21}{56} \)
\( \frac{-5}{7}<\frac{-39}{56}<\frac{-38}{56}<\frac{-29}{56}<\frac{-27}{56}<\frac{-22}{56} \) \( <\frac{-3}{8} \)
The five rational numbers between \( <\frac{-5}{7} \) and \( <\frac{-3}{8} \) are
\( \frac{-39}{56}, \frac{-38}{56}, \frac{-29}{56}, \frac{-27}{56}, \frac{-22}{56} . \)Haryana Board Class 7 Maths Solutions For Chapter 8 Exercise-8.1
1. List five rational numbers between: (1) -1 and 0 . (2) -2 and -1
(3) \( \frac{-4}{5} \text { and } \frac{-2}{3} \)
4. \( \frac{-1}{2} \text { and } \frac{2}{3} \)
Solution:
First we find equivalent rational numbers having same denominator.
1) \( -1=\frac{-1}{1}=\frac{-1 \times 10}{1 \times 10}=\frac{-10}{10} \)
\( 0=\frac{0}{1}=\frac{0 \times 10}{1 \times 10}=\frac{0}{10} \) \( \Rightarrow \frac{-10}{10}<\frac{-9}{10}<\frac{-8}{10}<\frac{-7}{10}<\frac{-6}{10}<\frac{-5}{10}<\frac{0}{10} \) \( \Rightarrow-1<\frac{-9}{10}<\frac{-8}{10}<\frac{-7}{10}<\frac{-6}{10}<\frac{-5}{10}<0 \)The five rational numbers between -1 and 0 are
\( \frac{-9}{10}, \frac{-8}{10}, \frac{-7}{10}, \frac{-6}{10}, \frac{-5}{10} \)Haryana Board Class 7 Maths Rational Numbers Solutions
2) – 2 and -1
Solution:
\( -2=\frac{-2}{1}=\frac{-2 \times 10}{1 \times 10}=\frac{-20}{10} \) \( -1=\frac{-1}{1}=\frac{-1 \times 10}{1 \times 10}=\frac{-10}{10} \) \( \begin{aligned}\Rightarrow \frac{-20}{10} & <\frac{-19}{10}<\frac{-18}{10}<\frac{-17}{10} \\
& <\frac{-16}{10}<\frac{-15}{10}<\frac{-10}{10}
\end{aligned} \) \( \begin{aligned}
\Rightarrow-2<\frac{-19}{10}<\frac{-18}{10}<\frac{-17}{10} & <\frac{-16}{10} \\
& <\frac{-15}{10}<-1
\end{aligned} \)
The five rational numbers between -2 and -1 are
\( \frac{-19}{10}, \frac{-18}{10}, \frac{-17}{10}, \frac{-16}{10}, \frac{-15}{10} \)HBSE 7th Class Rational Number Word Problems
3) \( \frac{-4}{5} \text { and } \frac{-2}{3} \)
Solution:
\( \frac{-4}{5}=\frac{-4 \times 9}{5 \times 9}=\frac{-36}{45} \) \( \frac{-2}{3}=\frac{-2 \times 15}{3 \times 15}=\frac{-30}{45} \) \( \begin{aligned}\Rightarrow \frac{-36}{45}<\frac{-35}{45} & <\frac{-34}{45}<\frac{-33}{45} \\
& <\frac{-32}{45}<\frac{-31}{45}<\frac{-30}{45}
\end{aligned} \) \( \begin{aligned}
\Rightarrow \frac{-4}{5}<\frac{-35}{45}<\frac{-34}{45}<\frac{-33}{45} & <\frac{-32}{45} \\
& <\frac{-31}{45}<\frac{-2}{3}
\end{aligned} \)
The five rational numbers between \( \frac{-4}{5} \) and \( \frac{-2}{3} \text { are } \) are
\( \frac{-35}{45}<\frac{-34}{45}<\frac{-33}{45}<\frac{-32}{45}<\frac{-31}{45} \)Class 7 Maths Chapter 8 Rational Numbers Haryana Board
4) \( \frac{-1}{2} \text { and } \frac{2}{3} \)
Solution:
\( \begin{aligned}& \frac{-1}{2}=\frac{-1 \times 3}{2 \times 3}=\frac{-3}{6} \\
& \frac{2}{3}=\frac{2 \times 2}{3 \times 2}=\frac{4}{6}
\end{aligned} \) \( \begin{aligned}
& \Rightarrow \frac{-3}{6}<\frac{-2}{6}<\frac{-1}{6}<0<\frac{1}{6}<\frac{2}{6}<\frac{4}{6} \\
& \Rightarrow-\frac{1}{2}<\frac{-2}{6}<\frac{-1}{6}<0<\frac{1}{6}<\frac{2}{6}<\frac{2}{3}
\end{aligned} \)
The five rational numbers between \( \frac{-1}{2} \text { and } \frac{2}{3} \text { are } \)
\( \frac{-2}{6}, \frac{-1}{6}, 0, \frac{1}{6}, \frac{2}{6} \)2. Write four more rational numbers in each of the following patterns :
1) \( \frac{-3}{5}, \frac{-6}{10}, \frac{-9}{15}, \frac{-12}{20} \ldots . . \)
Solution:
\( \frac{-3}{5}=\frac{-3 \times 1}{5 \times 1} ; \frac{-6}{10}=\frac{-3 \times 2}{5 \times 2} \) \( \frac{-9}{15}=\frac{-3 \times 3}{5 \times 3} ; \frac{-12}{20}=\frac{-3 \times 4}{5 \times 4} \)Thus, we observe a pattern in these numbers.
The next four numbers would be
\( \frac{-3 \times 5}{5 \times 5}=\frac{-15}{25} ; \frac{-3 \times 6}{5 \times 6}=\frac{-18}{30} \) \( \frac{-3 \times 7}{5 \times 7}=\frac{-21}{35} ; \frac{-3 \times 8}{5 \times 8}=\frac{-24}{40} \)The required four rational numbers are
\( \frac{-15}{25}, \frac{-18}{30}, \frac{-21}{35}, \frac{-24}{40} \)2) \( \frac{-1}{4}, \frac{-2}{8}, \frac{-3}{12}, \ldots . \)
Solution:
\( \frac{-1}{4}=\frac{-1 \times 1}{4 \times 1} ; \frac{-2}{8}=\frac{-1 \times 2}{4 \times 2} \) \( \frac{-3}{12}=\frac{-1 \times 3}{4 \times 3} \)Thus we observe a pattern in these numbers.
The next four numbers would be
\( \begin{aligned}& \frac{-1 \times 4}{4 \times 4}=\frac{-4}{16} ; \frac{-1 \times 5}{4 \times 5}=\frac{-5}{20} \\
& \frac{-1 \times 6}{4 \times 6}=\frac{-6}{24} ; \frac{-1 \times 7}{4 \times 7}=\frac{-7}{28}
\end{aligned} \)
The required four rational numbers are
\( \frac{-4}{16}, \frac{-5}{20}, \frac{-6}{24}, \frac{-7}{28} \)Haryana Board 7th Class Maths Rational Numbers Questions and Answers
3) \( \frac{-1}{6}, \frac{2}{-12}, \frac{3}{-18}, \frac{4}{-24}, \ldots \ldots \)
Solution:
\( \frac{2}{-12}=\frac{-1 \times(-2)}{6 \times(-2)} ; \frac{3}{-18}=\frac{-1 \times(-3)}{6 \times(-3)} \) \( \frac{4}{-24}=\frac{-1 \times(-4)}{6 \times(-4)} \)Thus we observe a pattem in these numbers.
\( \begin{aligned}&\frac{-1 \times(-5)}{6 \times(-5)}=\frac{5}{-30} ; \frac{(-1) \times(-6)}{6 \times(-6)}=\frac{6}{-36} ;\\
&\frac{(-1) \times(-7)}{6 \times(-7)}=\frac{7}{-42} ; \frac{(-1) \times(-8)}{6 \times(-8)}=\frac{8}{-48}
\end{aligned} \)
The required four numbers are \( \frac{5}{-30} ; \frac{6}{-36} \)
\( \frac{7}{-42}, \frac{8}{-48} \)4) \( \frac{-2}{3}, \frac{2}{-3}, \frac{4}{-6}, \frac{6}{-9} \ldots . \)
Solution:
\( \begin{aligned}&\frac{2}{-3}=\frac{-2 \times(-1)}{(-3) \times(-1)} ; \frac{4}{-6}=\frac{(-2) \times(-2)}{3 \times(-2)}\\
&\frac{6}{-9}=\frac{(-2) \times(-3)}{(3) \times(-3)}
\end{aligned} \)
Thus we observe a pattern in these numbers.
The next four numbers would be
\( \begin{aligned}&\frac{-2 \times(-4)}{3 \times(-4)}=\frac{8}{-12} ; \frac{(-2) \times(-5)}{3 \times(-5)}=\frac{10}{-15}\\
&\frac{(-2) \times(-6)}{3 \times(-6)}=\frac{12}{-18} ; \frac{(-2) \times(-7)}{3 \times(-7)}=\frac{14}{-21}
\end{aligned} \)
The required four numbers are
\( \frac{8}{-12} ; \frac{10}{-15} ; \frac{12}{-18} ; \frac{14}{-21} \)3. Give four rational numbers equivalent to:
(1)\( \frac{-2}{7} \)
(2)\( \frac{5}{-3} \)
(3)\( \frac{4}{9} \)
Solution:
(1)
\( \begin{aligned}& \frac{-2}{7}=\frac{-2 \times 2}{7 \times 2}=\frac{-4}{14} \\
& \frac{-2}{7}=\frac{-2 \times 3}{7 \times 3}=\frac{-6}{21} \\
& \frac{-2}{7}=\frac{-2 \times 4}{7 \times 4}=\frac{-8}{28} \\
& \frac{-2}{7}=\frac{-2 \times 5}{7 \times 5}=\frac{-10}{35}
\end{aligned} \)
Thefourrational numbers equivalent to \( \frac{-2}{7} \text { are } \frac{-4}{14}, \frac{-6}{21}, \frac{-8}{28}, \frac{-10}{35} \)
(2)\( \frac{5}{-3} \)
Solution:
\( \frac{5}{-3}=\frac{5 \times 2}{-3 \times 2}=\frac{10}{-6} \) \( \begin{aligned}& \frac{5}{-3}=\frac{5 \times 3}{-3 \times 3}=\frac{15}{-9} \\
& \frac{5}{-3}=\frac{5 \times 4}{-3 \times 4}=\frac{20}{-12} \\
& \frac{5}{-3}=\frac{5 \times 5}{-3 \times 5}=\frac{25}{-15}
\end{aligned} \)
The four rational numbers equivalent
\( \text { to } \frac{5}{-3} \text { are } \frac{10}{-6}, \frac{15}{-9}, \frac{20}{-12}, \frac{25}{-15} \)Sample Problems Rational Numbers Haryana Board Class 7
(3)\( \frac{4}{9} \)
Solution:
\( \begin{aligned}& \frac{4}{9}=\frac{4 \times 2}{9 \times 2}=\frac{8}{18} \\
& \frac{4}{9}=\frac{4 \times 3}{9 \times 3}=\frac{12}{27} \\
& \frac{4}{9}=\frac{4 \times 4}{9 \times 4}=\frac{16}{36} \\
& \frac{4}{9}=\frac{4 \times 5}{9 \times 5}=\frac{20}{45}
\end{aligned} \)
The four rational numbers equivalent to \( \frac{4}{9} \) are
\( \frac{8}{18}, \frac{12}{27}, \frac{16}{36}, \frac{20}{45} \)4. Draw the number line and represent the following rational numbers on it:
1) \( \frac{3}{4} \)
Solution:

2) \( \frac{-5}{8} \)
Solution:

3) \( \frac{-7}{4} \)
Solution:
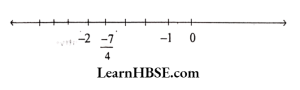
4) \( \frac{7}{8} \)
Solution:

5. The points P, Q, R, S, T, U, A, and B on the number line are such that, TR = RS = SU and AP= PQ = QB. Name the rational numbers represented by P, Q, R, and S.
Solution:

The points P, Q, R,S on the number line such that TR = RS = SU
\( \mathrm{TR}=\mathrm{RS}=\mathrm{SU}=\frac{1}{3} \mathrm{TU} \) \( \begin{aligned}& \mathrm{TR}=\frac{1}{3} \text { unit } \\
& \text { and } \mathrm{AP}=\mathrm{PQ}=\mathrm{QB} \\
& \mathrm{AP}=\mathrm{PQ}=\mathrm{QB}=\frac{1}{3} \mathrm{AB}
\end{aligned} \) \( \mathrm{AP}=\frac{1}{3} \text { unit. } \)
The rational number represented by P
\( P=2+\frac{1}{3}=\frac{6+1}{3}=\frac{7}{3} \)The rational number represented by Q,
\( \mathrm{Q}=2+\frac{1}{3}+\frac{1}{3}=\frac{6+1+1}{3}=\frac{8}{3} \)The rational number represented by R,
\( R=(-1)+\left(\frac{-1}{3}\right)=\frac{-1-3}{3}=\frac{-4}{3} \)The rational number represented by S,
\( S=(-1)+\left(\frac{-1}{3}\right)+\left(\frac{-1}{3}\right)=\frac{-3-1-1}{3}=\frac{-5}{3} \)6. Which of the following pairs represent the same rational number ?
1) \( \frac{-7}{21} \text { and } \frac{3}{9} \)
Solution:
\( \frac{-7}{21} \) is a negative rational number.
\( \frac{3}{9} \) is a positive rational number.
The given pair does not represent the same rational number.
2)
\( \frac{-16}{20} \text { and } \frac{20}{-25} \)
Solution:
\( \frac{-16}{20}=\frac{-16 \div 4}{20 \div 4}=\frac{-4}{5}=\frac{(-4) \times(-1)}{5 \times(-1)}=\frac{4}{-5} \) \( \frac{20}{-25}=\frac{20 \div 5}{-25 \div 5}=\frac{4}{-5} \)The given pair represents the same rational number
3) \( \frac{-2}{-3} \text { and } \frac{2}{3} \)
Solution:
\( \frac{-2}{-3}=\frac{(-2) \times(-1)}{(-3) \times(-1)}=\frac{2}{3} \)The given pair represents the same rational number.
4) \( \frac{-3}{5} \text { and } \frac{-12}{20} \)
Solution:
\( \frac{-3}{5}=\frac{-3 \times 4}{5 \times 4}=\frac{-12}{20} \)The given pair represents the same rational number.
5) \( \frac{8}{-5} \text { and } \frac{-24}{15} \)
\( \frac{8}{-5} \text { and } \frac{-24}{15} \) \( \frac{8}{-5}=\frac{8 \times 3}{-5 \times 3}=\frac{24}{-15}=\frac{24 \times(-1)}{(-15) \times(-1)}=\frac{-24}{15} \)The given pair represents the same rational number.
6) \( \frac{1}{3} \text { and } \frac{-1}{9} \)
Solution:
\( \frac{1}{3} \) is a positive rational number.
\( \frac{-1}{9} \) is a negative rational number.
The given pair does not represent the same rational number.
7) \( \frac{-5}{-9} \text { and } \frac{5}{-9} \)
Solution:
\( \frac{-5}{-9}=\frac{-5 \times(-1)}{-9 \times(-1)}=\frac{5}{9} \)\( \frac{5}{9} \) is a positive rational number.
\( \frac{5}{-9} \) is a negative rational number.
The given pair does not represent the same rational number.
Operations on Rational Numbers Class 7 HBSE
7. Rewrite the following rational numbers in the simplest form:
1) \( \frac{-8}{6} \)
Solution:
\( \frac{-8}{6} \)HCF of 8 and 6 is 2.
\( \frac{-8}{6}=\frac{-8 \div 2}{6 \div 2}=\frac{-4}{3} \)2) \( \frac{25}{45} \)
Solution:
\( \frac{25}{45} \)HCF of 25 and 45 is 5.
\( \frac{25}{45}=\frac{25 \div 5}{45 \div 5}=\frac{5}{9} \)Chapter 8 Rational Numbers Class 7 Solutions in Hindi Haryana Board
3) \( \frac{-44}{7 \cdot 2} \)
Solution:
\( \frac{-44}{7 \cdot 2} \)HCF of 44 and 72 is 4.
\( \frac{-44}{72}=\frac{-44 \div 4}{72 \div 4}=\frac{-11}{18} \)4) \( \frac{-8}{10} \)
Solution:
\( \frac{-8}{10} \)HCF of 8 and 10 is 2.
\( \frac{-8}{10}=\frac{-8 \div 2}{10 \div 2}=\frac{-4}{5} \)8. Fill in the boxes with the correct symbol out of >, < and =
1) \( \frac{-5}{7}\)  \( \frac{2}{3}\)
\( \frac{2}{3}\)
Solution:
LCM of 7 and 3 is 21.
\( \begin{aligned}& \frac{-5}{7}=\frac{-5 \times 3}{7 \times 3}=\frac{-15}{21} \\
& \frac{2}{3}=\frac{2 \times 7}{3 \times 7}=\frac{14}{21}
\end{aligned} \) \( \text { Hence } \frac{-5}{7}<\frac{2}{3} \)
2) \( \frac{-4}{5} \)  \( \frac{-5}{7} \)
\( \frac{-5}{7} \)
Solution:
LCM of 5 and 7 is 35
\( \frac{-4}{5}=\frac{-4 \times 7}{5 \times 7}=\frac{-28}{35} \) \( \begin{aligned}&\frac{-5}{7}=\frac{-5 \times 5}{7 \times 5}=\frac{-25}{35}\\
&\text { Hence } \frac{-4}{5}<\frac{-5}{7}
\end{aligned} \)
3) \( \frac{-7}{8} \)  \( \frac{14}{-16} \)
\( \frac{14}{-16} \)
Solution:
\( \begin{aligned}&\frac{-7}{8}=\frac{-7 \times(-2)}{8 \times(-2)}=\frac{14}{-16}\\
&\text { Hence } \frac{-7}{8}=\frac{14}{-16}
\end{aligned} \)
4) \( \frac{-8}{5} \)  \( \frac{-7}{4} \)
\( \frac{-7}{4} \)
Solution:
LCM of 5 and 4 is 20
\( \begin{aligned}&\begin{aligned}
& \frac{-8}{5}=\frac{-8 \times 4}{5 \times 4}=\frac{-32}{20} \\
& \frac{-7}{4}=\frac{-7 \times 5}{4 \times 5}=\frac{-35}{20}
\end{aligned}\\
&\text { Hence } \frac{-8}{5}>\frac{-7}{4}
\end{aligned} \)
5) \( \frac{1}{-3} \)  \( \frac{-1}{4} \)
\( \frac{-1}{4} \)
Solution:
LCM of3 and 4 is 12
\( \begin{aligned}&\begin{aligned}
& \frac{1}{-3}=\frac{1 \times 4}{-3 \times 4}=\frac{4}{-12}=\frac{4 \times(-1)}{(-12) \times(-1)}=\frac{-4}{12} \\
& \frac{-1}{4}=\frac{-1 \times 3}{4 \times 3}=\frac{-3}{12}
\end{aligned}\\
&\text { Hence } \frac{1}{-3}<\frac{-1}{4}
\end{aligned} \)
6) \( \frac{5}{-11} \)  \( \frac{-5}{11} \)
\( \frac{-5}{11} \)
Solution:
\( \begin{aligned}&\frac{5}{-11}=\frac{5 \times(-1)}{(-11) \times(-1)}=\frac{-5}{11}\\
&\text { Hence } \frac{5}{-11}=\frac{-5}{11}
\end{aligned} \)
Equivalent Rational Numbers Class 7 Haryana Board
7) 0 rec \( \frac{-7}{6} \)
Solution: \begin{aligned}
& 0=\frac{0}{6} \\
& \text { Hence } 0>\frac{-7}{6}
\end{aligned}
9. Which is greater in each of the following:
1) \( \frac{2}{3}, \frac{5}{2} \)
Solution:
LCM of 3 and 2 is 6
\( \begin{aligned}& \frac{2}{3}=\frac{2 \times 2}{3 \times 2}=\frac{4}{6} \\
& \frac{5}{2}=\frac{5 \times 3}{2 \times 3}=\frac{15}{6} \\
& \frac{15}{6}>\frac{4}{6}
\end{aligned} \) \( \frac{5}{2}>\frac{2}{3} \)
Important Questions for Class 7 Maths Chapter 8 Haryana Board
2) \( \frac{-5}{6}, \frac{-4}{3} \)
Solution: LCM of 6 and 3 is 6.
\( \begin{aligned}& \frac{-5}{6}=\frac{-5 \times 1}{6 \times 1}=\frac{-5}{6} \\
& \frac{-4}{3}=\frac{-4 \times 2}{3 \times 2}=\frac{-8}{6} \\
& \frac{-5}{6}>\frac{-8}{6}
\end{aligned} \) \( \frac{-5}{6}>\frac{-4}{3} . \)
3) \( \frac{-3}{4}, \frac{2}{-3} \)
LCM of 4 and 3 is 12.
Solution:
\( \begin{aligned}& \frac{-3}{4}=\frac{-3 \times 3}{4 \times 3}=\frac{-9}{12} \\
& \frac{2}{-3}=\frac{2 \times 4}{-3 \times 4}=\frac{8}{-12}=\frac{8 \times(-1)}{(-12) \times(-1)}=\frac{-8}{12}
\end{aligned} \) \( \begin{aligned}
&\frac{-8}{12}>\frac{-9}{12}\\
&\frac{-2}{3}>\frac{-3}{4}
\end{aligned} \) \( \frac{2}{-3}>\frac{-3}{4} \)
4) \( \frac{-1}{4}, \frac{1}{4} \)
Solution: \( \frac{1}{4}>\frac{-1}{4} \)
5) \( -3 \frac{2}{7},-3 \frac{4}{5} \)
Solution:
\( -3 \frac{2}{7}=\frac{-23}{7} \quad ; \quad-3 \frac{4}{5}=\frac{-19}{5} \)LCM of 7 and 5 is 35.
\( \begin{aligned}& \frac{-23}{7}=\frac{-23 \times 5}{7 \times 5}=\frac{-115}{35} \\
& \frac{-19}{5}=\frac{-19 \times 7}{5 \times 7}=\frac{-133}{35}
\end{aligned} \) \( \begin{aligned}
\frac{-115}{35} & >\frac{-133}{35} \\
\frac{-23}{7} & >\frac{-19}{5}
\end{aligned} \) \( \text { Hence }-3 \frac{2}{7}>-3 \frac{4}{5} \)
10. Write the following rational numbers in ascending order :
1) \( \frac{-3}{5}, \frac{-2}{5}, \frac{-1}{5} \)
Solution:
Denominators of each rational number is 5.
-3<-2<-l
\( \frac{-3}{5}<\frac{-2}{5}<\frac{-1}{5} \) \( \text { Ascending order is } \frac{-3}{5}, \frac{-2}{5}, \frac{-1}{5} \)2) \( \frac{-1}{3}, \frac{-2}{9}, \frac{-4}{3} \)
Solution: LCM of 3, 9, 3 is 9.
\( \frac{-1}{3}=\frac{-1 \times 3}{3 \times 3}=\frac{-3}{9} ; \frac{-2 \times 1}{9 \times 1}=\frac{-2}{9} \) \( \frac{-4}{3}=\frac{-4 \times 3}{3 \times 3}=\frac{-12}{9} \)-12 < -3 < -2

HBSE Class 7 Maths Chapter 8/9 Guide Rational Numbers
3) \( \frac{-3}{7}, \frac{-3}{2}, \frac{-3}{4} \)
Solution: LCM of 7, 2, 4 is 28.
\( \begin{aligned}& \frac{-3}{7}=\frac{-3 \times 4}{7 \times 4}=\frac{-12}{28} \\
& \frac{-3}{2}=\frac{-3 \times 14}{2 \times 14}=\frac{-42}{28}
\end{aligned} \) \( \begin{aligned}
\frac{-3}{4} & =\frac{-3 \times 7}{4 \times 7} \\
& =\frac{-21}{28}
\end{aligned} \)
– 42 < -21 < -12

& \frac{-42}{28}<\frac{-21}{28}<\frac{-12}{28} \\
& \frac{-3}{2}<\frac{-3}{4}<\frac{-3}{7}
\end{aligned} \) \( \text { Ascending order is } \frac{-3}{2}, \frac{-3}{4}, \frac{-3}{7} \)
Solutions To Try These
Find (1) \( \frac{-13}{7}+\frac{6}{7} \)
Solution: \( \frac{-13}{7}+\frac{6}{7}=\frac{-13+6}{7}=\frac{-7}{7}=-1 \)
2) \( \frac{19}{5}+\left(\frac{-7}{5}\right) \)
Solution: \( \frac{19}{5}+\frac{-7}{5}=\frac{19+(-7)}{5}=\frac{19-7}{5}=\frac{12}{5} \)
Solutions To Try These
Find:
(1) \( \frac{-3}{7}+\frac{2}{3} \)
Solution: LCM of 7 and 3 is 21.
\( \begin{aligned}& \frac{-3}{7}=\frac{-3 \times 3}{7 \times 3}=\frac{-9}{21} \\
& \text { and } \frac{2}{3}=\frac{2 \times 7}{3 \times 7}=\frac{14}{21}
\end{aligned} \) \( \frac{-3}{7}+\frac{2}{3}=\frac{-9}{21}+\frac{14}{21}=\frac{-9+14}{21}=\frac{5}{21} \)
2) \( \frac{-5}{6}+\frac{-3}{11} \)
Solution: LCM of 6 and 11 is 66
\( \frac{-5}{6}=\frac{-5 \times 11}{6 \times 11}=\frac{-55}{66} \text { and } \) \( \begin{aligned}&\frac{-3}{11}=\frac{-3 \times 6}{11 \times 6}=\frac{-18}{66}\\
&\frac{-5}{6}+\frac{(-3)}{11}=\frac{-55}{66}+\frac{(-18)}{66}=\frac{-55-18}{66}=\frac{-73}{66}
\end{aligned} \)
Solutions To Try These
What will be the additive inverse of \( \frac{-3}{9}, \frac{-9}{11}, \frac{5}{7} ? \)
Solution:
\( \text { Additive inverse of } \frac{-3}{9} \text { is } \frac{3}{9} \) \( \text { Additive inverse of } \frac{-9}{11} \text { is } \frac{9}{11} \) \( \text { Additive inverse of } \frac{5}{7} \text { is } \frac{-5}{7} \)Solutions To Try These
Find 1) \( \frac{7}{9}-\frac{2}{5} \)
Solution:
\( \frac{7}{9}+\frac{(-2)}{5}=\frac{35 \div(-18)}{45}=\frac{35-18}{45}=\frac{17}{45} \)2) \( 2 \frac{1}{5}-\frac{(-1)}{3} \)
Solution:
\( \begin{aligned}&2 \frac{1}{5}-\frac{(-1)}{3}=\frac{11}{5}+\text { Additive inverse of } \frac{-1}{3}\\
&\frac{11}{5}+\frac{1}{3}=\frac{33 \div 5}{15}=\frac{38}{15}=2 \frac{8}{15}
\end{aligned} \)
Solutions To Try These
What will be
1) \( \frac{-3}{5} \times 7 ? \)
Solution: \( \frac{-3}{5} \times 7=\frac{(-3) \times 7}{5}=\frac{-21}{5}=-4 \frac{1}{5} \)
2) \( \frac{-6}{5} \times(-2) ? \)
Solution: \( \frac{-6}{5} \times(-2)=\frac{(-6) \times(-2)}{5}=\frac{12}{5}=2 \frac{2}{5} \)
Important Concepts Rational Numbers Class 7 HBSE
Solutions To Try These
Find:
(1) \( \frac{-3}{4} \times \frac{1}{7} \)
Solution: \( \frac{-3}{4} \times \frac{1}{7}=\frac{(-3) \times 1}{4 \times 7}=\frac{-3}{28} \)
(2) \( \frac{2}{3} \times \frac{-5}{9} \)
Solution: \( \frac{2}{3} \times \frac{-5}{9}=\frac{2 \times(-5)}{3 \times 9}=\frac{-10}{27} \)
Solutions To Try These
What will be the reciprocal of \( \frac{-6}{11} \) and \( \frac{-8}{5} \) ?
Solution:
\( \text { The reciprocal of } \frac{-6}{11} \text { is } \frac{-11}{6} \) \( \text { The reciprocal of } \frac{-8}{5} \text { is } \frac{-5}{8} \)Solutions To Try These
Find:
(1) \( \frac{2}{3} \times \frac{-7}{8} \)
Solution:
\( \begin{aligned}& \frac{2 \times(-7)}{3 \times 8}=\frac{-14}{24} \\
& =\frac{-14 \div 2}{24 \div 2}=\frac{-7}{12}
\end{aligned} \)
2) \( \frac{-6}{7} \times \frac{5}{7} \)
Solution: \( \begin{aligned}
&\frac{-6}{7} \times \frac{5}{7}=\frac{(-6) \times 5}{7 \times 7}\\
&=\frac{-30}{49}
\end{aligned} \)
Step-by-Step Solutions for Rational Numbers Class 7 Haryana Board
Haryana Board Class 7 Maths Solutions For Chapter 8 Exercise-8.2
1. Find the sum:
1) \( \frac{5}{4}+\left(\frac{-11}{4}\right) \)
Solution:
\( \begin{aligned}& \frac{5}{4}+\left(\frac{-11}{4}\right)=\frac{5+(-11)}{4} \\
& =\frac{5-11}{4}=\frac{-6}{4}=\frac{-6 \div 2}{4 \div 2}=\frac{-3}{2}
\end{aligned} \)
2) \( \frac{5}{3}+\frac{3}{5} \)
\(\)
Solution: \( \frac{5}{3}+\frac{3}{5} \)
LCM of 3 and 5 is 15.
\( \frac{5}{3}=\frac{5 \times 5}{3 \times 5}=\frac{25}{15} \) \( \frac{3}{5}=\frac{3 \times 3}{5 \times 3}=\frac{9}{15} \) \( \frac{5}{3}+\frac{3}{5}=\frac{25}{15}+\frac{9}{15}=\frac{25+9}{15} \) \( =\frac{34}{15}=2 \frac{4}{15} \)3) \( \frac{-9}{10}+\frac{22}{15} \)
Solution: \( \frac{-9}{10}+\frac{22}{15} \)
LCM of 10 and 15 is 30.
\( \frac{-9}{10}=\frac{-9 \times 3}{10 \times 3}=\frac{-27}{30} \) \( \frac{22}{15}=\frac{22 \times 2}{15 \times 2}=\frac{44}{30} \) \( \frac{-9}{10}+\frac{22}{5}=\frac{-27}{30}+\frac{44}{30} \) \( =\frac{-27+44}{30}=\frac{17}{30} \)4) \( \frac{-3}{-11}+\frac{5}{9} \)
Solution:
LCM of 11 and 9 is 99.
\( \frac{-3}{-11}=\frac{3}{11}=\frac{3 \times 9}{11 \times 9}=\frac{27}{99} \) \( \frac{5}{9}=\frac{5 \times 11}{9 \times 11}=\frac{55}{99} \) \( \frac{-3}{-11}+\frac{5}{9}=\frac{27}{99}+\frac{55}{99}=\frac{27+55}{99}=\frac{82}{99} \)5) \( \frac{-8}{19}+\frac{(-2)}{57} \)
Solution:
LCM of 19 and 57 is 57
\( \frac{-8}{19}=\frac{-8 \times 3}{19 \times 3}=\frac{-24}{57} \) \( \begin{aligned}& \text { and } \frac{-2}{57}=\frac{-2 \times 1}{57 \times 1}=\frac{-2}{57} \\
& \frac{-8}{19}+\frac{(-2)}{57}=\frac{-24}{57}+\frac{(-2)}{57} \\
& =\frac{-24-2}{57}=\frac{-26}{57}
\end{aligned} \)
6) \( \frac{-2}{3}+0 \)
Solution: \( \frac{-2}{3}+\frac{0}{3}=\frac{-2+0}{3}=\frac{-2}{3} \)
7) \( -2 \frac{1}{3}+4 \frac{3}{5} \)
Solution: \( -2 \frac{1}{3}+4 \frac{3}{5}=\frac{-7}{3}+\frac{23}{5} \)
LCM of 3 and 5 is 15.
\( \begin{aligned}& \frac{-7}{3}=\frac{-7 \times 5}{3 \times 5}=\frac{-35}{15} \\
& \frac{23}{5}=\frac{23 \times 3}{5 \times 3}=\frac{69}{15} \\
& \frac{-7}{3}+\frac{23}{5}=\frac{-35}{15}+\frac{69}{15}
\end{aligned} \) \( =\frac{-35+69}{15}=\frac{34}{15}=2 \frac{4}{15} \)
2. Find:
1) \( \frac{7}{24}-\frac{17}{36} \)
Solution: \( \frac{7}{24}-\frac{17}{36}=\frac{7}{24}=\left(\frac{-17}{36}\right) \)
LCM of 24 and 36 is 72.
\( \frac{7}{24}=\frac{7 \times 3}{24 \times 3}=\frac{21}{72} \text { and } \frac{17}{36}=\frac{17 \times 2}{36 \times 2}=\frac{34}{72} \) \( \begin{aligned}\frac{7}{24}+\frac{(-17)}{36} & =\frac{21}{72}+\frac{(-34)}{72} \\
& =\frac{21+(-34)}{72}=\frac{-13}{72}
\end{aligned} \)
(2) \( \frac{5}{63}-\left(\frac{-6}{21}\right) \)
Solution:
\( \frac{5}{63}-\left(\frac{-6}{21}\right)=\frac{5}{63}+\frac{6}{21} \)LCM of 63 and 21 is 63.
\( \begin{aligned}\frac{5}{63} & =\frac{5 \times 1}{63 \times 1}=\frac{5}{63} \\
\frac{6}{21} & =\frac{6 \times 3}{21 \times 3}=\frac{18}{63} \\
& =\frac{5+18}{63}=\frac{23}{63}
\end{aligned} \)
Practice Problems Rational Numbers Class 7 Haryana Board
3) \( \frac{-6}{13}-\frac{(-7)}{15} \)
Solution: \( \frac{-6}{13}-\frac{(-7)}{15}=\frac{-6}{13}+\frac{7}{15} \)
LCM of 13 and 15 is 195.
\( \begin{aligned}& \frac{-6}{13}=\frac{-6 \times 15}{13 \times 15}=\frac{-90}{195} \\
& \frac{7}{15}=\frac{7 \times 13}{15 \times 13}=\frac{91}{195} \\
& \frac{-6}{13}+\frac{7}{15}=\frac{-90}{195}+\frac{91}{195}
\end{aligned} \) \( =\frac{-90+91}{195}=\frac{1}{195} \)
4) \( \frac{-3}{8}-\frac{7}{11} \)
Solution: \( \frac{-3}{8}-\frac{7}{11}=\frac{-3}{11}+\left(\frac{-7}{11}\right) \)
LCM of 8 and 11 is 88.
\( \begin{aligned}& \frac{3}{8}=\frac{3 \times 11}{8 \times 11}=\frac{33}{88} \text { and } \frac{7}{11}=\frac{7 \times 8}{11 \times 8}=\frac{56}{88} \\
& \frac{-3}{8}+\left(\frac{-7}{11}\right)=\frac{-33}{88}+\left(\frac{-56}{88}\right)
\end{aligned} \) \( \begin{aligned}
& =\frac{-33+(-56)}{88}=\frac{-89}{88} \\
& =-1 \frac{1}{88}
\end{aligned} \)
5) \( -2 \frac{1}{9}-6 \)
Solution: \( -2 \frac{1}{9}-6=\frac{-19}{9}-6=\frac{-19}{9}+\frac{(-6)}{1} \)
LCM of 9 and 1 is 9.
\( \begin{aligned}& \frac{19}{9}=\frac{19 \times 1}{9 \times 1}=\frac{19}{9} \text { and } \frac{6}{1}=\frac{6 \times 9}{1 \times 9}=\frac{54}{9} \\
& -2 \frac{1}{9}-6=\frac{-19}{9}+\frac{(-6)}{1}
\end{aligned} \) \( \begin{aligned}
& =\frac{-19}{9}+\left(\frac{-54}{9}\right)=\frac{-19+(-54)}{9} \\
& =\frac{-73}{9}=-8 \frac{1}{9}
\end{aligned} \)
3) Find the product
1) \( \frac{9}{2} \times\left(\frac{-7}{4}\right) \)
Solution: \( \frac{9}{2} \times\left(\frac{-7}{4}\right) \)
\( \begin{aligned}& =\frac{9 \times(-7)}{2 \times 4} \\
& =\frac{-63}{8} \\
& =-7 \frac{7}{8}
\end{aligned} \)
Haryana Board Class 7 Maths Exercise 8.1 Solutions
2) \( \frac{3}{10} \times(-9) \)
Solution: \( \frac{3}{10} \times(-9) \)
\( \begin{aligned}& =\frac{3 \times(-9)}{10} \\
& =\frac{-27}{10} \\
& =-2 \frac{7}{10}
\end{aligned} \)
3) \( \frac{-6}{5} \times \frac{9}{11} \)
Solution: \( \frac{-6}{5} \times \frac{9}{11} \)
\( \begin{aligned}& =\frac{-6 \times 9}{5 \times 11} \\
& =\frac{-54}{55}
\end{aligned} \)
4) \( \frac{3}{7} \times\left(\frac{-2}{5}\right) \)
Solution: \( \frac{3}{7} \times\left(\frac{-2}{5}\right) \)
\( \begin{aligned}& =\frac{3 \times(-2)}{7 \times 5} \\
& =\frac{-6}{35}
\end{aligned} \)
5) \( \frac{3}{11} \times \frac{2}{5} \)
Solution: \( \frac{3}{11} \times \frac{2}{5} \)
\( \begin{aligned}& =\frac{3 \times 2}{11 \times 5} \\
& =\frac{6}{55}
\end{aligned} \)
Key Questions in Rational Numbers for Class 7 HBSE
6) \( \frac{3}{-5} \times \frac{-5}{3} \)
Solution: \( \frac{3}{-5} \times \frac{-5}{3} \)
\( \begin{aligned}& =\frac{3 \times(-5)}{(-5) \times 3} \\
& =\frac{-15}{-15}=1
\end{aligned} \)
4. Find the value of:
1) \( (-4) \div \frac{2}{3} \)
Solution: \( (-4) \div \frac{2}{3} \)
\( =\frac{-4}{1} \div \frac{2}{3} \) \( \begin{aligned}& =\frac{-4}{1} \times \frac{3}{2} \\
& =\frac{(-4) \times 3}{1 \times 2} \\
& =\frac{-12}{2}
\end{aligned} \)
=-6
2) \( \frac{-3}{5} \div 2 \)
Solution:
\( \begin{aligned}& \frac{-3}{5} \div 2=\frac{-3}{5} \div \frac{2}{1} \\
& =\frac{-3}{5} \times \frac{1}{2} \\
& =\frac{-3 \times 1}{5 \times 2} \\
& =\frac{-3}{10}
\end{aligned} \)
3) \( \frac{-4}{5} \div(-3) \)
Solution:
\( \begin{aligned}& \frac{-4}{5} \div(-3)=\frac{-4}{5} \div \frac{(-3)}{1} \\
& =\frac{-4}{5} \times \frac{1}{-3}=\frac{-4 \times(-1)}{5 \times 3}=\frac{4}{15}
\end{aligned} \)
4) \( \frac{-1}{8} \div \frac{3}{4} \)
Solution:
\( \begin{aligned}& \frac{-1}{8} \div \frac{3}{4}=\frac{-1}{8} \times \frac{4}{3} \\
& =\frac{-1 \times 4}{8 \times 3} \\
& =\frac{-4}{24} \\
& =\frac{-4 \div 4}{24 \div 4} \\
& =\frac{-1}{6}
\end{aligned} \)
5) \( \frac{-2}{13} \div \frac{1}{7} \)
Solution:
\( \begin{aligned}& \frac{-2}{13} \div \frac{1}{7}=\frac{-2}{13} \times \frac{7}{1} \\
& =\frac{-2 \times 7}{13 \times 1} \\
& =\frac{-14}{13} \\
& =-1 \frac{1}{13}
\end{aligned} \)
6) \( \frac{-7}{12} \div\left(\frac{-2}{13}\right) \)
Solution:
\( \begin{aligned}& \frac{-7}{12} \div\left(\frac{-2}{13}\right) \\
& =\frac{-7}{12} \times\left(\frac{-13}{2}\right) . \\
& =\frac{-7 \times 13}{12 \times(-2)} \\
& =\frac{-91}{-24} \\
& =\frac{91}{24}=3 \frac{19}{24}
\end{aligned} \)
7) \( \frac{3}{13} \div\left(\frac{-4}{65}\right) \)
Solution:
\( \begin{aligned}& \frac{3}{13} \div\left(\frac{-4}{65}\right) \\
& =\frac{3}{13} \times \frac{65}{-4} \\
& =\frac{3 \times 65}{13 \times(-4)}=\frac{3 \times 5}{-4} \\
& =\frac{-15}{4}=-3 \frac{3}{4}
\end{aligned} \)
Additional Questions
Very Short Answer Questions
1. What is meant by a rational number?
Solution:
A number that can be expressed in the form of \( \frac{p}{q} \) where p and q are integers and q ≠ 0 is called a rational number.
2. How’ to write equivalent rational numbers?
Solution: If the numerator and denominator of a rational number are multiplied or divided by a non- zero integer we get a rational number which is said to be equivalent to the given rational number.
3. How to write rational numbers in the standard form?
Solution:
A rational number is said to be in the standard form if its denominator is a I positive integer and the numerator and denominator have no common factor
other than 1.
4) Reduce \( \frac{-75}{120}\) to the standard form.
Solution:
We have \( \begin{aligned}
& \frac{-75}{120}=\frac{-75+3}{120+3} \\
& =\frac{-25}{40}=\frac{-25+5}{40 \div 5}=\frac{-5}{8}
\end{aligned} \)
5. Compare \( \frac{-3}{5} \text { and } \frac{-1}{3} \)
Solution:
\( \begin{aligned}& \frac{-3}{5}=\frac{-3 \times 3}{5 \times 3}=\frac{-9}{15} \\
& \frac{-1}{3}=\frac{-1 \times 5}{3 \times 5}=\frac{-5}{15}
\end{aligned} \) \( \begin{aligned}
& \text { we have } \frac{-9}{15}<\frac{-8}{15}<\frac{-7}{15}<\frac{-6}{15}<\frac{-5}{15} \\
& \frac{-3}{5}<\frac{-8}{15}<\frac{-7}{15}<\frac{-6}{15}<\frac{-1}{3}
\end{aligned} \) \( \frac{-3}{5}<\frac{-1}{3} \)
6. \( \text { Add } \frac{-7}{5} \text { and } \frac{-2}{3} \text {. } \)
Solution:
LCM of 5 and 3 to 15
\( \begin{aligned}& \frac{-7}{5}=\frac{-7 \times 3}{5 \times 3}=\frac{-21}{15} \\
& \frac{-2}{3}=\frac{-2 \times 5}{3 \times 5}=\frac{-10}{15} \\
& \frac{-7}{5}+\frac{(-2)}{3}=\frac{-21}{15}+\frac{(-10)}{15} \\
& =\frac{-21 \cdot 10}{15}=\frac{-31}{15}
\end{aligned} \)
7. \( \text { Find } \frac{5}{7}-\frac{3}{8} \)
Solution: \( \frac{5}{7}-\frac{3}{8}=\frac{40-21}{56}=\frac{19}{56} \)
8. Find (1) \( \frac{-3}{5} \times 2 \)
Solution: \( \frac{-3 \times 2}{5}=\frac{-6}{5} \)
2) \( \frac{4}{9}+\frac{(-5)}{7} \)
Solution: \( \frac{4}{9}+\frac{(-5)}{7}=\frac{4}{9} \times \frac{7}{-5}=\frac{-28}{45} \)
9. Write five rational numbers which are smaller than \( \frac{5}{6} \).
Solution: \( \frac{5}{6}=\frac{50}{60} \)
We know that \( \frac{49}{60}, \frac{48}{60}, \frac{47}{60}, \frac{46}{60}, \frac{45}{60} \)………………… are smaller than \( \frac{50}{60} \).
\( \frac{49}{60}, \frac{48}{60}, \frac{47}{60}, \frac{46}{60}, \frac{45}{60} \)………… are any tive rational numbers smaller
than \( \frac{5}{6} \)
10. What number should \( \frac{-33}{16} \) by to get \( \frac{-11}{4} \)
Solution:
The number \( \frac{-33}{16} \) should be divided by to get \( \frac{-11}{4} \)
\( \begin{aligned}& =\frac{-33}{16} \div \frac{-11}{4} \\
& =\frac{-33}{16} \times \frac{4}{-11} \\
& =\frac{3}{4}
\end{aligned} \)
Short Answer Questions
11. Subtract :
1) \( \frac{3}{4} \text { from } \frac{1}{3} \)
Solution: \( \frac{1}{3}-\frac{3}{4} \)
\( =\frac{(4 \times 1)-(3 \times 3)}{12}=\frac{4-9}{12}=\frac{-5}{12} \)2) \( \frac{-32}{13} \text { from } 2 \)
Solution:
\( 2-\left(\frac{-32}{13}\right)=\frac{2}{1}+\frac{32}{13} \) \( =\frac{(13 \times 2)+(1 \times 32)}{13}=\frac{26+32}{13}=\frac{58}{13} \)3) \( -7 \text { from } \frac{-4}{7} \)
Solution: \( \frac{-4}{7}-(-7)=\frac{-4}{7}+\frac{7}{1} \)
\( =\frac{(1 \times-4)+(7 \times 7)}{7}=\frac{-4+49}{7}=\frac{45}{7} \)12. What numbers should be added to \( \frac{-5}{8} \) so as to get \( \frac{-3}{2} \) ?
Solution:
Suppose ‘x’ is the rational number to be
added to \( \frac{-5}{8} \text { to get } \frac{-3}{2} \)
Then, \( \frac{-5}{8}+x=\frac{-3}{2} \)
\( \Rightarrow x=\frac{-3}{2}-\left(\frac{-5}{8}\right) \) \( \begin{aligned}& \Rightarrow x=\frac{-3}{2}+\frac{5}{8} \\
& \Rightarrow x=\frac{(4 \times-3) \times(1 \times 5)}{8} \\
& \Rightarrow x=\frac{-12+5}{8}=\frac{-7}{8}
\end{aligned} \) \( x=\frac{-7}{8} \)
13. The sum of two rational numbers is 8. If one of the numbers is \( \frac{-5}{6} \) then find the other.
Solution: It is given that
Sum of the two numbers = 8 and one of the numbers = \( \frac{-5}{6} \)
Suppose the other rational number is x. Since the sum is 8
\( \begin{aligned}& \Rightarrow x+\left(\frac{-5}{6}\right)=8 \Rightarrow x=8-\left(\frac{-5}{6}\right) \\
& \Rightarrow x=\frac{8}{1}+\frac{5}{6} \\
& \Rightarrow x=\frac{(6 \times 8)+(1 \times 5)}{6} \\
& \Rightarrow x=\frac{48+5}{6}=\frac{53}{6}
\end{aligned} \)
The other number is \( \frac{53}{6} \)
14. Represent \( \frac{-13}{5} \) on the number line.
Solution:
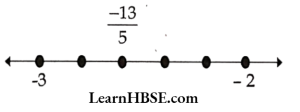
\( \frac{13}{5}=-2 \frac{3}{5}=-2-\frac{3}{5} \). This lies between – 2 and- 3 on the number line.
Divide the number line between- 2 and – 3 into 5 equal parts.
Mark 3rd part (numerator of rational part) counting from 2.
This is the place of the required rational number \( \frac{-13}{5} \)
15. Express each of the following decimal in the \( \frac{p}{q} \) form
- 0.57
- 0.176
- 1.00001
- 25.125
Solution:
1) \( 0.57=\frac{57}{100} \)
2) \( 0.176=\frac{176}{1000}=\frac{176 \div 8}{1000 \div 8}=\frac{22}{125} \)
3) \( 1.00001=\frac{100001}{100000} \)
4) \( \begin{aligned}
25.125 & =\frac{25125}{1000}=\frac{25125 \div 5}{1000 \div 5} \\
& =\frac{5025 \div 5}{200 \div 5}=\frac{1005 \div 5}{40 \div 5}=\frac{201}{8}
\end{aligned} \)
Long Answer Questions
16. Represent these numbers on the number line. (1) \( \frac{9}{7} \) (2) \( \frac{-7}{5} \)
Solution:

(1) \( \frac{9}{7}=1 \frac{2}{7}=1+\frac{2}{7} \).This lies between 1 and 2 on the number line.
Divide the number line between1 and 2 into 7 equal parts. Mark 2nd part countingfrom1
This is the place of the required rational number \( \frac{9}{7} \) .
(2)
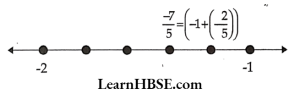
This lies between -1 and -2 on the number line.
Divide the number line between -1 and -2 into 5 equal parts.. Mark 2nd part counting from -1.
This is the place of rational number \( \frac{-7}{5} \)
17. Find a rational number between \( \frac{2}{3} \text { and } \frac{3}{4} \)
Solution:
\( \frac{2}{3}=\frac{2 \times 4}{3 \times 4}=\frac{8}{12} \) [Hint: First write the rational numbers with equal denominators]
\( \frac{3}{4}=\frac{3 \times 3}{4 \times 3}=\frac{9}{12} \) (Converting them into rational numbers with same denominators)
Now
\( \frac{8}{12}=\frac{8 \times 5}{12 \times 5}=\frac{40}{60} \text { and } \quad \frac{9}{12}=\frac{9 \times 5}{12 \times 5}=\frac{45}{60} \)Rational numbers between \( \frac{2}{3} \text { and } \frac{3}{4} \) may be taken as \( \frac{41}{60}, \frac{42}{60}, \frac{43}{60}, \frac{44}{60} \)
We can take any one of these.
(or)
We know that between two rational numbers x and y such that x < y, there is a rational \( \frac{x+y}{2} \)
i.e \( x<\frac{x+y}{2}<y \)
So, a rational number between \( \frac{2}{3} \text { and } \frac{3}{4} \text { is } \)
\( \frac{\frac{2}{3}+\frac{3}{4}}{2}=\frac{\frac{(4 \times 2)+(3 \times 3)}{12}}{2}=\frac{\frac{8+9}{12}}{2}=\frac{17}{12} \times \frac{1}{2}=\frac{17}{24} \)Thus we have \( \frac{2}{3}<\frac{17}{24}<\frac{3}{4} \).
18. Find ten rational numbers between \( \frac{-3}{4} \text { and } \frac{5}{6} \).
Solution: \( \frac{-3}{4}=\frac{-3 \times 6}{4 \times 6}=\frac{-18}{24} \)
\( \frac{5}{6}=\frac{5 \times 4}{6 \times 4}=\frac{20}{24} \)[Converting them to rational numbers with the same denominators]
Clearly -17, -16, -15, -14, -13, -12, -11, -10………………0,1,2,3………….are integers between numerators -18 and 20 of these equivalent rational numbers. Thus we have \( \frac{-17}{24}, \frac{-16}{24}, \frac{-15}{24}, \frac{-14}{24}, \frac{-13}{24}, \frac{-12}{24}, \frac{-11}{24}, \frac{-10}{24}, 0, \frac{1}{24} \) ……………………… as rational numbers between
\( \frac{-18}{24}\left(=\frac{-3}{4}\right) \text { and } \frac{20}{24}\left(=\frac{5}{6}\right) \)We can take any ten of these as required rational numbers.
Workbook
Choose the correct answers :
1. Which of these is a negative rational number
- 0
- \( \frac{5}{7} \)
- \(\frac{-5}{7}\)
- \(\frac{-5}{-7}\)
Answer: 3
2. The HCF of 45 and 30 is
- 15
- 30
- 45
- 1350
Answer: 1
3. \( \frac{3}{7}+\frac{(-6)}{7}= \)
- \( \frac{9}{7} \)
- \( \frac{-9}{7} \)
- \( \frac{3}{7} \)
- \( \frac{-3}{7} \)
Answer: 4
4. Additive inverse of \( \frac{-4}{7} \) is
- \( \frac{-7}{4} \)
- \( \frac{4}{7} \)
- \( \frac{-4}{7} \)
- \( \frac{-3}{7} \)
Answer: 2
5. LCM of 3 and 7 is
- 10
- 21
- 4
- 7
Answer: 2
6. How is \( \frac{7}{4} \) is expressed as a rational number with denominator 20?
- \( \frac{-70}{20} \)
- \( \frac{-35}{20} \)
- \( \frac{35}{20} \)
- B or C
Answer: 2
7. Express \( \frac{1}{4} \) and \( \frac{1}{3} \) with same denominator.
- \( \frac{4}{12} \text { and } \frac{3}{12} \)
- \( \frac{3}{12} \text { and } \frac{4}{12} \)
- \( \frac{4}{7} \text { and } \frac{3}{7} \)
- \( \frac{3}{7} \text { and } \frac{3}{7} \)
Answer: 2
8. \( -\frac{28}{84} \) can be expressed as a rational number as……..
- \( \frac{4}{7} \)
- \( \frac{-4}{12} \)
- \( \frac{4}{12} \)
- \( \frac{4}{-7} \)
Answer: 2
9. Which of the following is true?
Statement (1):
\( \frac{-9}{15}<\frac{-2}{3}<\frac{-4}{5} \)
Statement (2): \( \frac{-4}{5}<\frac{-2}{3}<\frac{-9}{15} \)
Statement (3): \( \frac{-2}{3}<\frac{-9}{15}<\frac{-4}{5} \)
- only (1)
- only (2)
- only (3)
- both (1) and (2)
Answer: 2
10. Which of the following are three rational numbers between -2 and -1?
- \( \frac{-1}{2}, \frac{-1}{3}, \frac{-1}{5} \)
- \( \frac{-3}{2}, \frac{-7}{4}, \frac{-5}{4} \)
- \( \frac{-12}{5}, \frac{-22}{5}, \frac{12}{5} \)
- \( \frac{3}{2}, \frac{7}{4}, \frac{5}{4} \)
Answer: 2
11. A rational number between \( \frac{-2}{3} \text { and } \frac{1}{4} \) is…………
- \( \frac{5}{12} \)
- \( \frac{-5}{12} \)
- \( \frac{5}{24} \)
- \( \frac{-5}{24} \)
Answer: 4
12. If \( \frac{p}{q} \) is the fractional form of 0.36 then p + q =…………..
- 15
- 17
- 19
- 21
Answer: 1
13. The denominator of afractionwhich equals to the decimal fraction of 0.125 is………….
- 900
- 1000
- 999
- 990
Answer: 3
14. 0.9 + 9.1 =……….
- 9.91
- 9.19
- 10.1
- 10.1
Answer: 3
15. The reciprocal of 9 lies in the number system…….
- N
- W
- Z
- N and W
Answer: 3
16. The sum of two rational numbers is 8 and one of them is \( \frac{-5}{6} \).Then the second number is……………….
Answer: 1
17. Which of the rational numbers
\( \frac{-11}{28}, \frac{-5}{7}, \frac{-9}{14}, \frac{-29}{42} \) is the greatest?
- \( \frac{-11}{28} \)
- \( \frac{-5}{7} \)
- \( \frac{-9}{14} \)
- \( \frac{-29}{42} \)
Answer: 1
18. \( \frac{7}{8}-\frac{2}{3}= \) = ……………..
Answer: 2
19. \( \text { If } \frac{x}{9}=\frac{4}{x} \text { then } x= \)…………..
Answer: 4
20. Which of the following is not a rational number ?
- \( \frac{-2}{3} \)
- -0.3
- π
- 0
Answer: 3
21. Rama : \( \frac{5}{3} \) is a rational number and 5 is only a natural number.
Shyama: Both \( \frac{5}{3} \) and 5 are rational numbers.
Which of the statements are true?
- Both Rama and Shyama
- Only Rama
- Only Shyama
- Neither Rama nor Shyama
Answer: 3
22. Which of the following is different among the following rationals ?
- \( \frac{1}{7} \)
- \( \frac{2}{3} \)
- \( \frac{27}{8} \)
- \( \frac{145}{6} \)
Answer: 3
23. 0.4 + 0.3 + 0.2 =………
- 0.432
- 0.432
- 0.1
- 1
Answer: 4
24. \( \frac{2 . \overline{9}}{4 . \overline{9}}=\)……….
- \( \frac{1}{2} \)
- \( \frac{3}{5} \)
- 1
- not defined
Answer: 2
25. A bus is moving at an average speed of \( 60 \frac{2}{5} \)km/hr.How much distance it will cover in \( 7 \frac{1}{2} \)
- 423 km
- 433 km
- 443 km
- 453 km
Answer: 4
26. The area of a rectangular park whose length is \( 36 \frac{3}{5} \)m and breadth is \( 16 \frac{2}{3} \)m………
- 1830 m²
- 1220 m²
- 610 m²
- 305 m²
Answer: 3
27.
- 10x = 157.3232………
- 1000 x = 15732.3232………
- Subtracting we get x = \( x=\frac{15575}{990} \)
- Let x = 15.732
Arrange the steps in order to express 15.732 in \( x=\frac{p}{q} \)
- 2, 1, 3, 4
- 4, 2, 1, 3
- 3, 1, 2, 4
- 4, 2, 3, 1
Answer: 2
28. Identify the rational number A marked in the following number line.
- \( x=\frac{3}{7} \)
- \( x=\frac{4}{6} \)
- \( x=\frac{4}{7} \)
- \( x=\frac{5}{7} \)
Answer: 3
29. Write the rational numbers for the points labelled with letters P, Q, R, S in order on the number line
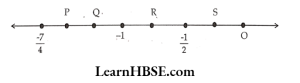
- \( \frac{-3}{2}, \frac{-5}{4}, \frac{-3}{4}, \frac{-1}{4} \)
- \( \frac{-1}{4}, \frac{-3}{4}, \frac{-5}{4}, \frac{-3}{2} \)
- \( \frac{6}{4}, \frac{5}{4}, \frac{3}{4}, \frac{1}{4} \)
- \( \frac{1}{4}, \frac{3}{4}, \frac{5}{4}, \frac{6}{4} \)
Answer: 1
30. Which letter of the number indicates \( \frac{17}{5} \)?

- A
- B
- C
- D
Answer: 2
Fill in the blanks :
31. All integers and fractions are…………..
Answer: rational numbers
32. Equivalent rational number for \( \frac{-3}{7} \) is………..
Answer: \( \frac{-6}{14} \)
33. The number…………. is neither a positive nor a negative rational number
Answer: zero
34. There are……….. number of rational numbers between any two rational numbers.
Answer: infinite
35. Both the numerator and the denominator of a rational number are positive then it is called a……………..
Answer: positive rational number
36. Match the following:
1. Reduce to standard form \( \frac{-3}{-15} \) ( ) A) \( \frac{1}{4} \)
2.Which is greater \( \frac{-1}{4}, \frac{1}{4} \) ( ) B) \( \frac{10}{9} \)
3. The additive inverse of \( \frac{5}{7} \) ( ) C) \( \frac{-5}{7} \)
4) \( \frac{-2}{9} \times(-5)= \) ( ) D) \( \frac{-15}{2} \)
5) \( (-5) \div \frac{2}{3}= \) ( ) E) \( \frac{1}{5} \)
Answer:
1. E 2. A 3. C 4. B 5. D
