Haryana Board Class 9 Maths Solutions For Chapter 4 Linear Equations In Two Variables

Haryana Board Class 9 Maths Solutions For Chapter 4 Linear Equations In Two Variables

• Equation: An equation is a statement in which one expression equals to another expression.
  Eg: 2x + 3 = 7y
  5m – 9 = 0
  3 + 6 = 9
  3\(x^2\)-5x+6=0
• Linear equation in one variable: An equation with only one variable of degree one is called linear equation in one variable. (or) An equation of the form ax + b = 0, where a, and b are real numbers such that a ≠ 0, is called a linear equation in one variable.
  Eg: 5x + 6 = 7; 3p = -7
• Standard form: ax + b = 0, where a and b ∈ R and a ≠ 0.
• Solution: A linear equation in one variable has a number that can satisfy the equation. This numbers are called the solution of the linear equation in one ” variable.
  • Linear equation has unique solution.

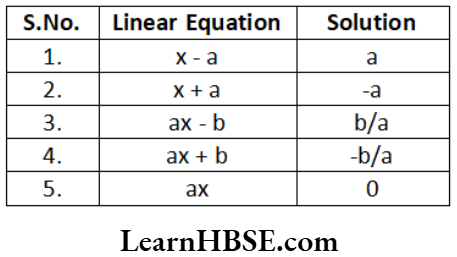
• Linear equation in two variables
  • An equation with two variables both of degree one is called linear equation in two variables. (or) An equation of the form ax + by + c = 0, where a, b and c are real numbers such that a ≠ 0 and b ≠ 0, is called a linear equation in two variables.
    Eg: 7a + 3b = 12
    2x = 3y – 5
  • Standard form: ax + by + c = 0, where a, b, c ∈ R and a, b ≠ 0.
• Solution of linear equation in two variables:
  A linear equation in two variables has a pair of numbers that can satisfy the equations. This pair of numbers is called the solution of the linear equation in two variables.
  • There are infinitely many solutions for a single linear equation in two variables.
  • The process of finding solution(s) is called solving an equation.
  • The solution of a linear equation is not affected when
    • the same number is added to (subtracted from) both sides of the equation.
    • both sides of the equation are mutiplied or divided by the same non-zero number.
• Graphical representation of linear equations:
  • Any linear equation in the standard form ax + by + c = 0 has a pair of solutions (x,y), that can be represented in the coordinate plane.
  • The graph of every linear equation in two variables (ax + by + c = 0) is a straight line.
  • Every point on the graph of a linear equation in two variables is a solution of the linear equation.
  • Every solution of the linear equation is a point on the graph of the linear equation.
  • The linear equation with constant value zero (in ax + by + c = 0, c = 0) passes through origin.
  • An equation of the type y = mx represents a straight line passing through the origin. Certain linear equations exist such that their solution is (0,0).
• Steps to draw the graph of linear equations in two variables:
  • Step 1: Let the given equation be ax + by + c = 0.
  • Step 2: Make the y as subject. i.e., y = \(-\left(\frac{a x+c}{b}\right)\)
  • Step 3: Take any 2 values (Most probably integrals) to x and calculate the values of y to obtain solutions (ordered pairs).
  • Step 4: Plot the ordered pairs on the graph paper on a suitable
  • Step 5: Draw the line passing through plotted points.
    Now the obtained line represents the equation: ax + by + c = 0.
    Note: We can take more than 2 values to x to get more solutions to check the correctness of the graph.
• Equations of the lines parallel to the coordinate axes:
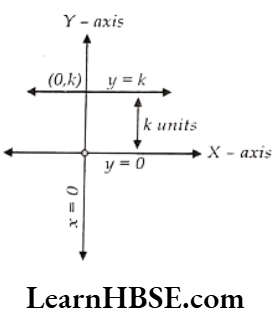
  • The equation of the X-axis: y = 0.
  • The equation of the Y-axis: x = 0.
  • The equation of the straight line parallel to X-axis: y = k. It lies at k units from X-axis and passes through (0,k).

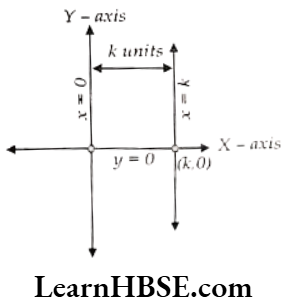
• • The equation of straight line parallel to Y-axis: x = k. It lies at k units from Y-axis and passes through (k, 0).

Haryana Board Class 9 Maths Chapter 4 Solutions

Haryana Board Class 9 Maths Solutions For Chapter 4 Linear Equations In Two Variables Exercise – 4.1

Question 1. The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.

Solution. Let the cost of a notebook = ₹ x

Let the cost of a pen = ₹ y

The cost of a notebook is twice the cost of a pen.

Cost of a notebook = 2 × cost of a pen

⇒ x = 2xy

⇒ x = 2y

⇒ x – 2y = 0

∴ Required equation

Question 2. Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:

Solution. (1) 2x + 3y = 9.35

Given equation: 2x + 3y = 9.35

⇒ 2x + 3y – 9.35 = 0

⇒ 2x + 3y + (-9.35) = 0

On comparing with ax + by + c = 0,

We get, a = 2,b = 3,c = -9.35

(2) Given equation: x – \(\frac{y}{5}\) – 10 = 0

⇒ \(x+\left(-\frac{1}{5}\right) y+(-10)=0\)

On comparing with ax + by + c = 0,

We get, a = 1, b = [latex-\frac{1}{5}[/latex], c = -10

(3) Given equation: -2x + 3y = 6

⇒ -2x + 3y – 6 = 0

On comparing with ax + by + c = 0,

We get, a = -2, b = 3, c = -6

(4) Given equation: x = 3y

⇒ x – 3y = 0

⇒ x + (-3)y + 0 = 0

On Comparing with ax + by + c = 0,

We get, a = 1, b = -3, c = 0

(5) Given equation: 2x = -5y

⇒ 2x + 5y = 0

⇒ 2x + 5y + 0 = 0

On comparing with ax + by + c = 0,

We get, a = 2, b = 5, c = 2.

(6) Given equation: x = 3y

⇒ x – 3y = 0

⇒ x + (-3)y + 0 = 0

On comparing with ax + by + c = 0,

We get, a = 1, b = -3, c = 0.

(5) Given equation : 2x = -5y

⇒ 2x + 5y = 0

⇒ 2x + 5y + 0 = 0

On comparing with ax + by + c = 0,

We get, a = 2, b = 5, c = 0.

(6) Given equation: 3x + 2 = 0

⇒ 3x + (0)y + 2 = 0

On comparing with ax + by + c = 0,

We get, a = 3, b = 0, c = 2.

(7) Given equation: y – 2 = 0

⇒ 0(x) – 1(y) – 2 = 0

On comparing with ax + by + c = 0,

We get, a = 0,b = 1, c = -2.

(8) Given equation: 5 = 2x

⇒ 2x – 5 = 0

⇒ 2x + (0)y + (-5) = 0

On comparing with ax + by + c = 0,

We get, a = 2, b = 0, c = -5.

Class 9 Maths Chapter 4 Important Questions Haryana Board

Haryana Board Class 9 Maths Solutions For Chapter 4 Linear Equations In Two Variables Exercise – 4.2

Question 1. Which one of the following options is true, and why?

(1) A unique solution

(2) Only two solutions

(3) Infinitely many solutions

Solution. A linear equation in two variables has infinitely many solutions.

So, y = 3x + 5 has infinitely many solutions. So, option (3) is correct.

Question 2. Write four solutions for each of the following equations:

(1) 2x + y = 7

Solution. Given equation: 2x + y = 7

⇒ y = 7 – 2x

(a) Let x = 0 ⇒ y = 7 – 2(0) = 7 – 0 = 7.

Here solution = (0,7).

(b) Let x = 1 ⇒ y = 7 – 2(1) = 7 – 2 = 5.

Here solution = (1,5)

(c) Let x = -1 ⇒ y = 7 – 2(-1) = 7 + 2 = 9.

Here solution = (-1,9).

(d) Let x = 2 ⇒ y = 7 – 2(2) = 7 – 4 = 3.

Here solution = (2, 3).

∴ The solutions are (0,7), (1, 5), (-1, 9), (2, 3).

(2) πx + y = 9

Solution. Given equation: πx + y = 9

⇒ y = 9 – πx

(a) Let x = 0 ⇒ y = 9 – π(0) = 9 – 0 = 9.

Here solution = (0,9)

(b) Let x = 1 ⇒ y = 9 – π(1) = 9 – π

Here solution = (1, 9 – π)

(c) Let x = -1 ⇒ y = 9 – π(-1) = 9 + π

Here solution = (-1, 9 + π)

(d) Let x = 2 ⇒ y = 9 – π(2) = 9 – 2π

Here solution = (2, 9 – 2π)

∴ The solutions are (0,9), (1, 9 – π), (-1, 9 + π), (2, 9 – 2π)

(3) x = 4y

Solution. Given equation: x = 4y

⇒ y = \(\frac{x}{4}\)

(a) Let x = 0 ⇒ y = \(\frac{0}{4}\) = 0

Here solution = (0,0).

(b) Let x = 1 ⇒ y = \(\frac{1}{4}\)

Here solution = (1,7).

(c) Let x = 4 ⇒ y = \(\frac{4}{4}\) = 1

Here solution (4, 1).

(d) Let x = 2 ⇒ y = \(\frac{2}{4}\) = \(\frac{1}{2}\)

Here solution = (2, \(\frac{1}{2}\))

∴ The solutions are (0,0), (1, \(\frac{1}{4}\)), (4,1), (2,\(\frac{1}{2}\)).

Step-by-step Solutions for Class 9 Maths Chapter 4 Haryana Board

Question 3. Check which of the following are solutions of the equation x – 2y = 4 and which are not:

(1)(0, 2)

(2) (2,0)

(3) (4,0)

(4) (√2,4√2)

(5) (1,1)

Given equation: x – 2y = 4

Solution. (1) (0,2)

Substitute x = 0 and y = 2

LHS = x – 2y = 0 – 2(2) = 0 – 4 = -4 ≠ RHS

∴ (0, 2) is not a solution of the given equation.

(2) (2, 0)

Substitute x = 2 and y = 0

LHS = x – 2y = 2 – 2(0) = 2 – 0 = 2 ≠ RHS

∴ (2, 0) is not a solution of the given equation.

(3) (4,0)

Substitute x = 4 and y = 0

LHS = x – 2y = 4 – 2(0) = 4 – 0 = 4 = RHS

∴ (4,0) is a solution of the given equation.

(4) (√2,4√2)

Substitute x = √2 and y = 4√2

LHS = x – 2y = √2 – 2(4√2)

= √2 – 8√2 = -7√2 ≠ RHS

∴ (√2, 4√2) is not a solution of the given equation.

(5) (1,1)

Substitute x = 1 and y = 1

LHS = x – 2y = 1 – 2(1) = 1 – 2 = -1 ≠ RHS

∴ (1, 1) is not a solution of the given equation.

Question 4. Find the value of K, if x = 2, y = 1 is a solution of the equation 2x + 3y = K.

Solution. Given equation 2x + 3y = K.

x = 2, y = 1 is a solution.

on substituting x = 2 and y = 1.

⇒ 2(2) + 3(1) = K

4 + 3 = K

7 = K

∴ K = 7

Haryana Board Class 9 Maths Solutions For Chapter 4 Linear Equations In Two Variables Very Short Answer Type Questions

Question 1. Define linear equation in two variables.

Solution. An equation of the form ax + by + c = 0, where a, b and c are real numbers such that a ≠ 0 and b ≠ 0, is called a linear equation in two variables.

Question 2. Panth and Pandya scored 125 runs together. Express the information in the form of an equation.

Solution. Let the runs scored by Panth = x

Let the runs scored by Pandya = y

Total runs = 125

⇒ x + y = 125

Graphical Method of Solving Linear Equations Class 9 Haryana Board

Question 3. Express each of the equation y = 3 in the form of ax + by + c = 0 and write the values of a, b and c.

Solution. Given equation : y = 3

⇒ 0.x + y + (-3) = 0

On comparing with ax + by + c = 0,

We get, a = 0, b = 1, c = -3.

Question 4. Express each of the equation x – 5 = √3y in the form of ax + by + c = 0 and write the values of a, b and c.

Solution. Given equation: x – 5 = √3y

⇒ x – √3y – 5 = 0

⇒ x +(-√3)y + (-5) = 0

On comparing with ax + by + c = 0,

We get, a = 1, b = -√3,c = -5.

Question 5. How many solutions does a linear equation in two variables have?

Solution. A linear equation in two variables has infinitely many solutions.

Question 6. How many linear equations in two variables exist for which (2, 4) is a solution?

Solution. There are infinitely many linear equations in two variables exist for which (2, 4) is a solution.

Example: x + y = 6; x – y = -2; y = 2x.

Question 7. Write any two linear equations in two variables whose solution is (6,2).

Solution. Given solution: (6,2)

Sum of x-coordinate and y coordinate = 8 ⇒ x + y = 8

Difference of x-coordinate and y coordinate ⇒ 4x – y = 4

Question 8. Check whether (2, -5) is a solution of equation 2x + 5y = 2 or not.

Solution. Given equation : 2x + 5y = 2

Substitute x = 2 and y = -5

LHS = 2x + 5y = 2(2) + 5(-5)

= 4 – 25 = -21 ≠ RHS

∴ (2,-5) is not a solution of the given equation.

Question 9. Check whether (5, 0) is a solution of equation x + 3y = 5 or not.

Solution. Given equation: x + 3y = 5

Substitute x = 5 and y = 0

LHS = x + 3y = 5 + 3(0)

= 5 + 0 = 5 = RHS

∴ (5, 0) is a solution of the given

Question 10. Find 2 different solutions of x + y = 9

Solution. Given equation: x + y = 9

⇒ y = 9 – x

(a) Let x = 0 ⇒ y = 9 – 0 = 9.

Here solution = (0,9).

(b) Let x = 2 ⇒ y = 9 – 2 = 7.

Here solution = (2,7).

Question 11. Find two different solutions of 4x + y = 3.

Solution. Given equation: 4x + y = 3

⇒ y = 3 – 4x

(a) Let x = 0 ⇒ y = 3 – 4(0) = 3-0 = 3.

Here solution = (0,3).

(b) Let x = 2 ⇒ y = 3 – 4(2) = 3 – 8 = -5

Here solution = (2,-5).

Question 12. Which type of graph of a linear equation ax + by + c = 0 (Here a, b and c ∈ R & a ≠ 0, b ≠ 0) represents?

Solution. The graph of every linear equation in two variables (ax + by + c = 0) is a straight line.

Question 13. If (2, 0) is a solution of the linear equation 5x – 4y = k, then find the value of k.

Solution. Given equation: 5x – 4y = k

(2, 0) is a solution.

On substituting, x = 2 and y = 0.

⇒ 5(2) – 4(0) = k

⇒ 10 – 0 = k

⇒ 10 = k

∴ k = 10

Question 14. Write the equations of coordinate axes x and y.

Solution. The equation of the X-axis: x = 0

The equation of the Y-axis: y = 0

Question 15. Linear equation x – 2 = 0 is parallel to which axis?

Solution. Given equation: x – 2 = 0 ⇒ x = 2.

It is in the form of x = k.

∴ It is parallel to Y-axis.

Question 16. Write the equation of the line parallel to y-axis and passing through the point (-7,3).

Solution. The equation of the straight line parallel to Y-axis: x = k

Required equation: x = -7

⇒ x + 7 = 0

Question 17. Write the equation of the line parallel to X-axis and passing through the point (-2,-4)

Solution. The equation of the straight line parallel to X-axis: y = k

∴ Required equation: y = -4

⇒ y + 4 = 0

Question 18. Write the equation of three lines that are parallel to X-axis

Solution. The equation of three lines that are parallel to X-axis:

(1) y = 2

(2) y + 9 = 0

(3) 2y = 3

Question 19. Write the equation of three lines that are parallel to Y-axis

Solution. The equation of three lines that are parallel to X-axis:

(1) x = -2

(2)x – 9 = 0

(3) 5x = -3

Question 20. Find the distance between the graph of x – 5 = 0 and the Y-axis.

Solution. Given equation: x – 5 = 0 ⇒ x = 5

The graph of x = k is a straight line parallel to Y-axis. It lies at k units from Y-axis.

∴ The distance between the graph of x – 5 = 0 and the Y-axis is 5 units.

Question 21. Find the distance between the graph of 2y – 5 = 0 and the X-axis.

Solution. Given equation: 2y – 5 = 0 ⇒ x = 2.5

The graph of y k is a straight line parallel to X-axis. It lies at k units from X-axis.

∴ The distance between the graph of 2y – 5 = 0 and the Y-axis is 2.5 units.

Haryana Board Class 9 Maths Solutions For Chapter 4 Linear Equations In Two Variables Short Answer Type Questions

Question 22. Bhargavi got 10 more marks than double of the marks of Sindhu. Express the information in the form of an equation.

Solution. Let marks got by Bhargavi = x

Let marks got by Sindhu = y

Given that Bhargavi got 10 more marks than double of the marks Sindhu

∴ x = 10 + 2y

⇒ x – 2y – 10 = 0

Question 23. A number is 27 more than the number obtained by reversing its digits. If its units and tens digits are x and y respectively, write the linear equation representing the above statement.

Solution. Let the digit in units place = x

Let the digit in tens place = y

The number = 10y + x

If we reverse the digits, then the new number = 10x + y

From problem,

(Two-digit number) – (number formed by reversing the digits) = 27.

i.e., 10y + x – (10x + y) = 27

⇒ 10y + x – 10x – y – 27 = 0

⇒ 9y – 9x – 27 = 0

⇒ y – x – 3 = 0

⇒ x – y + 3 = 0

Haryana Board 9th Class Maths Chapter 4 Exercise Solutions

Question 24. The cost of a ball pen is 5 less than half the cost of a fountain pen. Write a linear equation in two variables to rep- resent this statement.

Solution. Let the cost of fountain pen = ₹ x

Let the cost of ball pen = ₹ y

Given that the cost of a ball pen is 5 less than half the cost of a fountain pen.

⇒ y = \(\frac{x}{2}\) – 5

⇒ 2y = x – 10

⇒ x – 2y = 10

Question 25. If x = 2k + 1 and y = k is a solution of the equation 5x + 3y – 7 = 0, find the value of k.

Solution. Given equation: 5x + 3y – 7 = 0

x = 2k + 1 and y = k is a solution of the equation.

On substituting, x = 2k + 1 and y = k.

⇒ 5(2k+1) – 3(k) – 7 = 0

⇒ 10k + 5 – 3k – 7 = 0

⇒ 7k – 2 = 0

⇒ 7k = 2

⇒ k = \(\frac{2}{7}\)

Question 26. Find 4 different solutions of 5x + y = 3

Solution. Given equation: 5x + y = 3

⇒ y = 3 – 5x

(a) Let x = 0 ⇒ y = 3 – 5(0) = 3 – 0 = 3.

Here solution = (0,3).

(b) Let x = 1 ⇒ y = 3 – 5(1) = 3 – 5 = -2.

Here solution = (1,-2).

(c) Let x = -1 ⇒ y = 3 – 5(-1) = 3 + 5 = 8.

Here solution = (-1, 8).

(d) Let x = 2 ⇒ y = 3 – 5(2) = 3 – 10 = -7

Here solution (2, -7).

(e) ∴ The solutions are

(0,3), (1, -2), (-1, 8), (2, -7).

Question 27. At which point the graph of the linear equation 2x – 3y = 6 cuts the Y-axis.

Solution. Given equation: 2x – 3y = 6

The x-coordinate of any point on the y-axis is zero.

Let the point of the line cuts the y-axis is (0, a).

On substituting, x = 0 and y = a.

⇒ 2(0) – 3(a) = 6

⇒ 0 – 3a = 6

⇒ -3a = 6

⇒ a = \(-\frac{6}{3}\)

⇒ a = -2

∴ The required point = (0, -2).

Haryana Board Class 9 Maths Solutions For Chapter 4 Linear Equations In Two Variables Long Answer Type Questions

Question 28. If (0, a) and (b, 0) are the solutions of the following linear equation 2x – 3y = 6. Find ‘a’ and ‘b’.

Solution. Given equation: 2x – 3y = 6.

(0, a) is one of the solutions of equation.

On substituting, x=0 and y = a.

⇒ 2(0) – 3(a) = 6

⇒ 0 – 3n = 6

⇒ -3a = 6

⇒ a = \(-\frac{6}{3}\)

⇒ a = -2

(b, 0) is another solution of equation.

On substituting, x = b and y = 0.

⇒ 2(b) – 3(0) = 6

⇒ 2b – 0 = 6

⇒ 2b = 6

⇒ b = \(\frac{6}{2}\)

⇒ b = 3

∴ a = -2 and b = 3

Haryana Board Class 9 Maths Solutions For Chapter 4 Linear Equations In Two Variables Objective Type Questions

Multiple Choice Questions:

Question 1. Which of the following is an equation?

1. 2x + 3 ≠ 4
2. 3x + y – 3
3. 7x – 7
4. 3m²+ m = 1

Answer. 4. 3m² + m = 1

Question 2. General form of linear equation in two variables is where a, b, c ∈ R and a and b ≠ 0.

1. ax + b = c
2. ax + by = cz
3. ax + by + c = 0
4. ay + bx = c

Answer. 3. ax + by + c = 0

Question 3. Sankar and Sanvi collected 100 together. Suitable equation for this information is

1. x + y + 100 = 0
2. x + y = 100
3. x – y = 100
4. x – y = -100

Answer. 2. x + y = 100

MCQ Questions on Linear Equations in Two Variables Class 9 Haryana Board

Question 4. On comparing 4x – y = 0 with ax + by + c = 0, we get c =

1. 4
2. -1
3. 0
4. -4

Answer. 3. 0

Question 5. On comparing -y = 0 with ax + by + c = 0, we get a + b + c =.

1. -1
2. 0
3. -2
4. 3

Answer. 1. -1

Question 6. The linear equation 2x+5 has _______ solution(s).

1. Unique
2. two
3. No
4. Infinitely many

Answer. 1. Unique

Question 7. The linear equation 2x + y = 5 has _______ solution(s).

1. Unique
2. two
3. No
4. Infinitely many

Answer. 4. Infinitely many

Question 8. The linear equation x + y = 5 has _______ natural solution(s).

1. Unique
2. two
3. No
4. Infinitely many

Answer. 1. Unique

Question 9. The solution of equation x – 2y = 4 are

(1)(0-2)

(2) (8.0)

(3)(6, 1)

(4) (-2,3)

1. (1) only
2. (1) & (3) only
3. (2) & (4) only
4. (4) only

Answer. 2. (1) & (3) only

Question 10. Number of linear equations in x and y can be satisfied by x=1 and y = 2 is

1. one
2. two
3. zero
4. Infinitely many

Answer. 4. Infinitely many

Question 11. If (2, 0) is a solution of the linear equation 2x + 3y = k, then the value of k is:

1. 4
2. -4
3. 3
4. 5

Answer. 1. 4

Question 12. x = 9, y = 4 is a solution of the linear equation

1. x + y + 13 = 0
2. x – y = 5
3. x – y + 5 = 0
4. x + y = -5

Answer. 2. x – y = 5

Question 13. (3,1) is the solution of the equation

1. 2x – y = 7
2. x – 2y = -7
3. 2x + y = 7
4. x – 2y = 7

Answer. 3. 2x + y = 7

Question 14. (2,-1) is the solution of the equation

(1) 3x + y = 5

(2) 2x – y = 5

(3) x + y + 1 = 0

(4) x + 2y = 1

1. (1) & (2) only
2. (1) & (3) only
3. (3) & (4) only
4. (4) only

Answer. 1. (1) & (2) only

Question 15. If x = -2 and y = 3 is the solution of equation x + 2y = k, then k=

1. 4
2. -4
3. 3
4. 5

Answer. 1. 4

Question 16. The geometrical representation of linear equation in two variables is

1. Straight line
2. Circle
3. Parabola
4. Triangle

Answer. 1. Straight line

Class 9 Maths Chapter 4 Theorems and Formulas Haryana Board

Question 17. For the equation 5x – 7y = 35, if y = 5, then the value of ‘x’ is

1. -14
2. 0
3. 14
4. 10

Answer. 3. 14

Question 18. The straight line passing through the points (0,0), (-1, 1) and (1, -1) has the equation

1. x – y = 0
2. x + y = 0
3. x + y = -1
4. x – y = 1

Answer. 2. x + y = 0

Question 19. Any point of the form (a, a) always lies on the graph of the equation

1. x – y = 0
2. x + y = 0
3. x + y = -1
4. x – y = 1

Answer. 1. x – y = 0

Question 20. Which of the following is not a solution of 2x – y + 3 = 0?

1. (3,9)
2. (0,3)
3. (-1,1)
4. (-1,-2)

Answer. 4. (-1,-2)

Question 21. The graph of the equation 2x + 3y = 6 cuts the X-axis at the point

1. (3,0)
2. (0,-3)
3. (-2,0)
4. (0,2)

Answer. 1. (3,0)

Question 22. The graph of linear equation x + 2y = 2, cuts the Y-axis at the point

1. (1,0)
2. (0,-3)
3. (-2,0)
4. (0,1)

Answer. 4. (0,1)

Question 23. Which of the following is true?

1. The line y = 2 parallel to Y-axis.
2. The line y – 3 = 0 parallel to X-axis.
3. The line y = 2 passes through (2,0)
4. The line y – 3 = 0 passes through (-3,0)

Answer. 2. The line y – 3 = 0 parallel to X-axis.

Question 24. Which of the following is not a solution of 3x – y = 6?

1. (0, -6)
2. (2, 0)
3. (-1,9)
4. (1,-3)

Answer. 3. (-1,9)

Question 25. The value of k if x = 2, y = 1 is a solution of equation 2x – k = -3y is

1. 7
2. 6
3. -6
4. -7

Answer. 1. 7

Question 26. Which of the following lines pass through origin?

(1) √3x + 3y = 0

(2) 4y = 3

(3) 5x = 2

(4) 4y = 3y

1. (1) & (2) only
2. (2) & (3) only
3. (3) & (4) only
4. (1) & (4) only

Answer. 4. (1) & (4) only

Question 27. The equation 2x+5y= 7 has a unique solution, if x, y are _______ numbers.

1. natural
2. integers
3. rational
4. real

Answer. 1. natural

Linear Equations in Two Variables Word Problems Class 9 Haryana Board

Question 28. A linear equation in two variables is of the form ax + by + c = 0 where

(1) a ≠ 0

(2) b ≠ 0

(3) c ≠ 0

(4) c = 0

1. (1) & (2) only
2. (2) & (3) only
3. (3) & (4) only
4. (4) only

Answer. 1. (1) & (2) only

Question 29. A linear equation in two variables is of the form ax + by + c = 0 passes through origin if

(1) a = 0

(2) b ≠ 0

(3) c ≠ 0

(4) c = 0

1. (1) & (2) only
2. (2) & (3) only
3. (3) & (4) only
4. (4) only

Answer. 4. (4) only

Question 30. The number of linear equations in 2 variables passes through 2 distinct points is

1. one
2. two
3. zero
4. Infinitely many

Answer. 1. one

Question 31. The positive solutions of the equation ax + by + c = 0 always lie in

1. 1st Quadrant
2. 2nd Quadrant
3. 3rd Quadrant
4. 4th Quadrant

Answer. 1. 1st Quadrant

Question 32. If we multiply or divide both sides of a linear equation with a non-zero number, then the solution of the linear equation

1. Changes
2. Remains the same
3. Changes in case of multiplication only
4. Changes in case of division only

Answer. 2. Remains the same

Question 33. Which of the following equation has graph parallel to Y-axis?

1. x = 3
2. y = 5
3. 2x + 3y = 0
4. 2x = 3y

Answer. 1. x = 3

Question 34. Which of the following equation has graph parallel to X-axis ?

1. 4x = 3
2. y + 6 = 0
3. 2x – y = 0
4. 2x + 4y = 8

Answer. 2. y + 6 = 0

Question 35. The equation of the line parallel to X-axis and passing through the point

1. y – 3 = 0
2. y + 3 = 0
3. y + 2 = 0
4. y – 2 = 0

Answer. 2. y + 3 = 0

36-40: Direction: There are two statements are given in each question. Select the options as the following.

1) Both statements are true

2) Statement A is true, statement B is false.

3) Both statements are false

4) Statement A is false, statement B is true.

Question 36. Statement A: The linear equation 2x – 5y = 7 has infinitely many solutions.

Statement B: Only one linear equation in x and y can be satisfied by x = 1 and y = 2.

Answer. 2. Statement A is true, statement B is false.

Question 37. Statement A: (1, -4) is one of the solution of equation x – 2y = 9.

Statement B: The equation x + y = 5 has only one pair of natural number solutions.

Answer. 1. Both statements are true

Question 38. Statement A: Equation of Y-axis is : y = 0.

Statement B: y = 2 line parallel to y axis.

Answer. 3. Both statements are false

Question 39. Statement A: The line 3x + 5y = 0 passes through origin.

Statement B: The y = x passes through (4,4).

Answer. 1. Both statements are true

Question 40. Statement A: The line parallel to the Y-axis at a distance 4 units to the left of Y-axis is x = -4.

Statement B: The equation of X-axis is of the form y = 0.

Answer. 4. Statement A is false, statement B is true.

41-50: Assertion and Reasoning questions

Direction: In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as

1) Both assertion and reason are true and reason is the correct explanation of assertion.

2) Both assertion and reason are true but reason is not the correct explanation of assertion.

3) Assertion is true but reason is false.

4) Assertion is false but reason is true.

Question 41. Assertion: There are infinite number of lines which passes through (-3,5)

Reason: A linear equation in two variables has infinitely many solutions.

Answer. 1. Both assertion and reason are true and reason is the correct explanation of assertion.

Question 42. Assertion: The graph of the equation 3x + y = 0 is a line passing through the origin.

Reason: An equation of the form ax + by + c = 0, where a, b, c R and a0, b0 is a linear equation in x and y.

Answer. 1. Both assertion and reason are ture and reason is the correct explanation of assertion.

Question 43. Assertion: The point (0, 3) lies on the graph of the linear equation 3x + 4y = 12.

Reason: (0, 3) satisfies the equation 3x + 4y = 12.

Answer. 2. Both assertion and reason are true but reason is not the correct explanation of assertion.

Question 44. Assertion The graph of the linear equation x – 2y = 1 passes through the point (-1, -1)

Reason: The linear equation x – 2y = 1 has unique solution.

Answer. 3. Assertion is true but reason is false.

Question 45. Assertion: The point (2, 2) lies on the line y = x

Reason: Any point on the line y = x is of the form (a, a)

Answer. 1. Both assertion and reason are true and reason is the correct explanation of assertion.

Question 46. Assertion: A linear equation 2x + 3y = 5 has a unique solution.

Reason: There are infinitely many solutions for a linear equation in two variables.

Answer. 4. Assertion is false but reason is true.

Question 47. Assertion: The graph of a line 3x – 4y + 12 = 0 intersects Y-axis at (0,3).

Reason: The line ax + by + c = 0 intesects X-axis at (\(-\frac{c}{a}\),0).

Answer. 2. Both assertion and reason are true but reason is not the correct explanation of assertion.

Question 48. Assertion: All the points (0, 0), (0,5), (0,3) and (0, 6) lie on the Y-axis.

Reason: Equation of the Y-axis is x = 0.

Answer. 1. Both assertion and reason are true and reason is the correct explanation of assertion.

Question 49. Assertion: The line y = 5x passes through origin..

Reason: The linear equation y = mx + c (c+0) passes through origin.

Answer. 3. Assertion is true but reason is false.

Question 50. Assertion: The geometric representation of x = -2 meets the X-axis at (0, -2).

Reason: The line y = k is parallel to X-axis and passes through the point (0, k).

Answer. 4. Assertion is false but reason is true.

Haryana Board Class 9 Maths Solutions For Chapter 4 Linear Equations In Two Variables Match the following:

Question 51. Match the following linear equations and points on those lines.

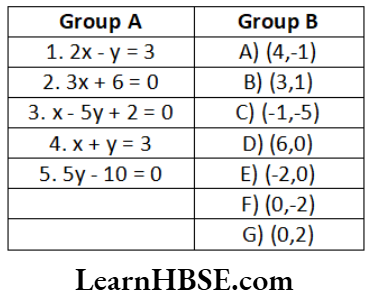
Answer. 1 – C, 2 – E, 3 – B, 4 – A, 5 – G.

Question 52. Match the following with suitable equations

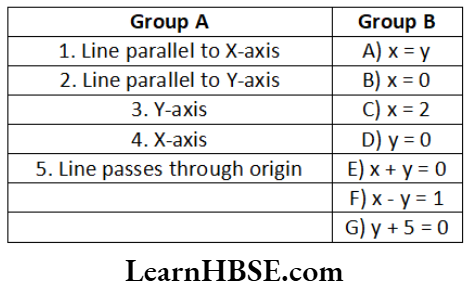
Answer. 1 – G, 2 – C,3 – B, 4 – D, 5 – A.

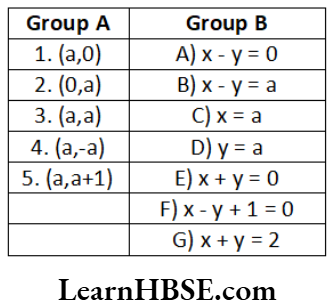
Question 53. Match the following general form of points with their equations. (Here a ≠ 0)

Answer. 1 – C, 2 – D, 3 – A, 4 – E, 5 – F.

Haryana Board Class 9 Maths Solutions For Chapter 4 Linear Equations In Two VariablesTrue or False Questions

Question 54. Any equation which can be put in the form ax + by + c = 0, where a, b and c are real numbers, and a and b are not both zero is called a linear equation in two variables

Answer. True

Question 55. 5x – 3 = 2x is a linear equation in one variable

Answer. True.

Question 56. 3x – y² = 5 is a linear equation in two variables

Answer. False

Question 57. ax² + by + c = 0 where a, b and c are real numbers, is a linear equation in two variables.

Answer. False

Question 58. There are infinitely many solutions for a given linear equation in two variables

Answer. True

Question 59. 3x + 5 = 0 has a unique solution

Answer. True

Question 60. The linear equation 2x + 5y = 7 has unique natural solutions.

Answer. True

Question 61. The linear equation 2x – 3y = 4 has unique solution.

Answer. False

Question 62. The point of the form (a,a) always lies on X-axis

Answer. False

Question 63. The graph of every linear equation in two variables need not be a line

Answer. False

Question 64. (0,2) is a solution for x – 2y = 4

Answer. False

Question 65. The point (0,-3) lies on the graph of the linear equation 3x + 4y = 12

Answer. True

Question 66. The graph of the linear equation x + 2y = 7 passes through the point (0,7)

Answer. False

Question 67. The graph of linear equation 2x – 3y = 0 is a line parallel to X-axis

Answer. False

Question 68. The line x – y = 4 intersects X-axis at (4,0)

Answer. True

Question 69. The line ax + by + c = 0 intersects Y-axis at (0, \(-\frac{c}{a}\))

Answer. False

Question 70. The line ax + by + c = 0 passes through origin if c = 0.

Answer. True

Question 71. (3, -3) lies on x + y = 3.

Answer. False

Question 72. The line passes through (4,7) and parallel to X-axis is y = 7.

Answer. True

Question 73. The line passes through (-3,7) and parallel to Y-axis is x – 3 = 0

Answer. False

Question 74. The line y = -3 intersects Y-axis at (0,-3)

Answer. True

Question 75. The line x + 2 = 0 intersects Y-axis at (0,-2)

Answer. False

Question 76. The line y = mx passes through origin.

Answer. True

Question 77. x = 0 is the equation of the X-axis.

Answer. False

Question 78. The linear equation 3x + 2 = 0 represents a line parallel to Y-axis.

Answer. True

Question 79. The graph of y = 6 is a line parallel to X-axis at a distance 6 units from the X-axis

Answer. True

Haryana Board Class 9 Maths Solutions For Chapter 4 Linear Equations In Two Variables Fill in the Blanks:

Question 80. A statement in which one expression equals to another expression is _______

Answer. equation

Question 81. An equation with only one variable of degree one is called as _______ equation in one variable.

Answer. linear

Question 82. General form of linear equation in one variable is _______

Answer. ax + b = 0

Question 83. Solution of linear equation ax + b = 0 is _______

Answer. –\(\frac{b}{a}\)

Question 84. An equation with two variables both of degree one is called as _______ equation in _______ variables.

Answer. linear, 2

Question 85. General form of linear equation in two variables is _______

Answer. ax + by + c = 0

Question 86. The number of solutions of linear equations in two variables is _______

Answer. infinite

Question 87. The graph of every linear equation in two variables (ax + bt + c = 0) is a _______

Answer. line

Question 88. If x = 1 and y = 1 is one of the solutions of x – y = k then k = _______

Answer. 0

Question 89. All the points (2,0), (-3,0), and (5,0) lie on the _______ axis.

Answer. x

Question 90. All the points (0,3), (0,0), (0,-4) and (0,7) lie on the _______ axis.

Answer. y

Question 91. Abscissa of all points on the Y-axis is _______

Answer. 0

Question 92. The negative solutions of the equation ax + by + c = 0 always lie in the _______ quadrant.

Answer. 3rd

Question 93. The positive solutions of the equation ax + by + c = 0 always lie in the _______ quadrant.

Answer. 1st

Question 94. If the point (3,4) lies on the graph of 3y = ax + 7, then the value of a = _______

Answer. \(\frac{5}{3}\)

Question 95. The line ax + by + c = 0 intersects X-axis at _______

Answer. (-\(\frac{c}{a}\), 0)

Question 96. The graph of the linear equation 2x + 3y = 6 is a line which meets the X-axis at _______

Answer. (3,0)

Question 97. The graph of the linear equation 3x – 4y – 12 = 0 is a line which meets the Y-axis at _______

Answer. (0,-3)

Question 98. The value of y if x = 2 in the linear equation 3x – 4y – 12 = 0 is _______

Answer. 3

Question 99. The value of x for which y = -4 is a solution of the linear equation 5x – 8y = 40 is _______

Answer. \(\frac{8}{5}\)

Question 100. An ordered pair that satisfy an equation in two variables is called its _______

Answer. solution

Question 101. If x = 1 and y = 0 is the solution of equation 2x + y = 3a, then the value of a _______

Answer. \(\frac{2}{3}\)

Question 102. If (3,-2) is a solution of the equation 3x – py – 7 = 0, then the value of p is _______

Answer. -1.

Question 103. If 7x – 3y = k passes through origin, then k = _______

Answer. 0

Question 104. The point of the form (a,a) always lies on _______

Answer. x = y

Question 105. The equation x = 7, in two variables, can be written as _______

Answer. 1.x + 0.y – 7 = 0

Question 106. If (a,1) lies on the graph of 3x – 2y + 4 = 0, then a = _______

Answer. –\(\frac{2}{3}\)

Question 107. The area of a triangle formed by coordinate axes and line x + y = 4 is _______

Answer. 8 sq. units

Question 108. The area of a rectangle formed by coordinate axes, line x = 2 and y = 6 is _______

Answer. 12 sq. units

Question 109. The line passes through (0,p) and parallel to X-axis is _______

Answer. y = p

Question 110. The linear equation such that each point on its graph has an ordinate 3 times its abscissa _______

Answer. y = 3x

Question 111. The line y = mx passes through _______

Answer. origin

Question 112. The equation of the X-axis is _______

Answer. y = 0

Question 113. The line parallel to the Y-axis at a distance 4 units to the left of Y-axis is given by the equation _______

Answer. x + 4 = 0

Question 114. The graph of y = 6 is a line parallel to _______ axis.

Answer. x

Question 115. The line x + 3 = 0 passes through _______ and _______ quadrants.

Answer. 2nd, 3rd

Question 116. The line passes through (-6,-5) and parallel to Y-axis is _______

Answer. x + 6 = 0

Question 117. The line passes through (-2,-3) and parallel to X-axis is _______

Answer. y + 3 = 0

Question 118. The line x + 2 = 0 intersects X-axis at _______

Answer. (-2,0)

Question 119. The line y = 2 intersects Y-axis at _______

Answer. (0,2)