Adiabatic and Isothermal Processes

Thermodynamics

First And Second Law Of Thermodynamics Isothermal And Adiabatic Process

Isothermal Process Definition: A process in which the temperature of a system remains constant is called an isothermal process. The changes in volume, pressure, and other quantities in iso-thermal processes are called isothermal changes.

Let a gas be enclosed inside a metallic cylinder-piston arrangement. The cylinder and the piston are made of a conducting material. The piston can move without friction along the inner walls of the cylinder.

• Now, if the gas expands very slowly, external work is done by the gas. As a result, the internal energy of the gas will tend to fall, as it supplies the energy necessary to do the work.
• But the internal energy of a gas depends on its temperature. So the temperature of the gas will also tend to fall. As metal is a good conductor of heat and the expansion of the gas is very slow, heat will enter the metallic cylinder from its surroundings and keep the temperature of the gas constant.
• This is called an isothermal expansion because there is no change in temperature during expansion.

Similarly, if the gas contracts very slowly, work is done on the gas. For that, heat is evolved, and the temperature of the gas increases. As the compression of the gas is very slow, heat evolved will be transmitted to the surroundings through the conducting cylinder, so that the temperature of the gas remains constant Such type of compression of a gas is called isothermal compression.

For an ideal gas, if the temperature remains constant, the internal energy also remains constant.

So, \(U_f=U_i \quad \text { or, } U_f-U_i=0\)

Then from the first law of thermodynamics,

Q = \(\left(U_f-U_i\right)+W=0+W \text { or, } Q=W\)

i.e., heat taken from the surroundings = external work done.

For an isothermal compression, both Q and W are negative. This means that work is done on the system by its surroundings and the system loses an equal amount of heat.

Isothermal conditions In Thermodynamic:

1. The heat exchange between the system and its surroundings should occur very fast. So the gas should be kept in a good conducting container and surrounded by a medium of high thermal capacity.
2. The process should be very slow so that the time is sufficient for heat exchange to keep the temperature constant. Because this expansion or compression of a gas should take place very slowly, an isothermal process is a very slow process, and any slow thermal process is usually regarded as isothermal.

Isothermal process of an ideal gas on a pV-diagram: For n mol of an ideal gas, pV = nRT. For an isothermal process, T = constant.

So, pV = constant.

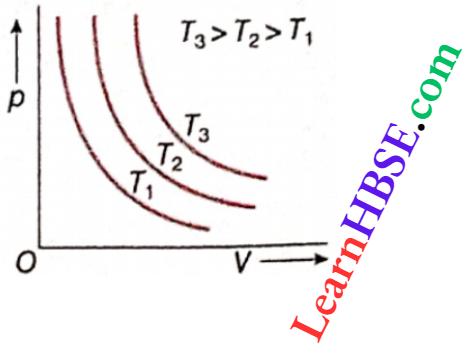
This equation is represented by a rectangular hyperbola on a pV diagram, Isothermal processes at higher temperatures have higher values of RT, i.e., higher values of pV. So the corresponding curves will be at greater distances from the origin.

The curves shown are called isothermal curves for an ideal gas. No two curves can intersect, because a point of intersection denotes two values of temperature of a gas simultaneously. This can never happen.

Adiabatic and Isothermal Processes 

Work done by an ideal gas in an isothermal process: For a change in volume dV at constant temperature of a certain amount of an ideal gas, work done dW = pdV. If the volume changes from Vi to Vj, the total work done is

W = \(\int_{V_i}^{V_f} p d V\)

= the area ABCDA on the pV-diagram

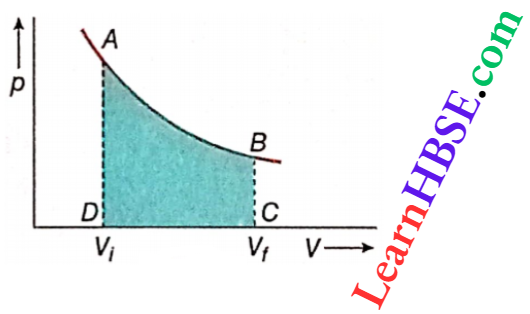
For n mol of an ideal gas, pV = nRT or, p = \(\frac{n R T}{V}\).

For an isothermal process, T = constant.

∴ \(W =\int_{V_i}^{V_f} \frac{n R T}{V} d V=n R T \int_{V_i}^{V_f} \frac{d V}{V}\)

= \(n R T \ln \frac{V_f}{V_i} \quad\left[\ln x=\log _e x\right]\)

Again, from Boyle’s law for an isothermal process,

⇒ \(p_i V_i=p_f V_f \quad \text { or, } \frac{V_f}{V_i}=\frac{p_i}{p_f}\)

So, \(W=n R T \ln \frac{V_f}{V_i}=n R T \ln \frac{p_i}{p_f}\)…(1)

For isothermal expansion, \(V_f>V_i\), so the ratio \(V_f / V_i\) is greater than 1.

Hence. W = \(n R T \ln \frac{V_f}{V_i}>0\)

Now for an isothermal compression of a gas, W = \(n R {In}\frac{V_f}{V_i}<0\).

So for an isothermal expansion, work done is positive while for an isothermal compression, associated work done is negative.

For an ideal gas, U = constant, when T = constant. So from the first law of thermodynamics,

Q = (U_f – U_i) + W = 0 + W = W.

Thus from equation (1),

Q = \(n R T \ln \frac{V_f}{V_i}=n R T \ln \frac{p_i}{p_f}\)….(2)

Adiabatic Process In Thermodynamics: A process in which no heat is exchanged between a system and its surroundings, is called an adiabatic process. The changes in volume, pressure, temperature, and other quantities in an adiabatic process are called adiabatic changes.

• Let a gas be enclosed inside a cylinder-piston arrangement. The cylinder and the piston are made of a non-conducting material. This piston can move without friction along the inner walls of the cylinder. When the gas expands rapidly, work is done by die gas.
• The internal energy of the gas decreases, as it supplies die energy necessary to do the work. However, the internal energy of a gas depends on its temperature. So the temperature of the gas wall also decreases.
• As the walls of the cylinder are non-conducting and the expansion of gas takes place very fast, no heat can enter from the surroundings to stop this fall in temperature. So there will be no heat exchange during this expansion.
• This is called an adiabatic expansion. The corresponding fall in temperature is known as adiabatic cooling.
• Similarly, if the gas contracts rapidly, work is done on the gas. Hence, heat is generated, and temperature of the gas increases.
• As the gas is compressed very fast, the heat evolved will not be transmitted to the surroundings through the non-conducting cylinder and the gas will remain hot.
• Such type of compression of the gas is called adiabatic compression and the corresponding rise in temperature is known as adiabatic heating.

In an adiabatic process, no heat is exchanged. So Q = 0. Then from the first law of thermodynamics, Q = (U_f – U_i) +W

or, 0 = ( U_f– U_i) + W

or, W = -(U_f– U_i) = -ΔU

i.e., external work done = decrease in internal energy.

For adiabatic compression, W is negative. This means that work is done on the system by its surroundings. As a result, the internal energy increases.

Adiabatic and Isothermal Processes 

Adiabatic Conditions In Thermodynamics:

1. In an adiabatic change, temperature does not remain constant. No heat should be exchanged between a system and its surroundings during this process. So the containers should be made of highly non-conducting materials. Here, the walls of the containers are known as adiabatic walls. A common example is the walls of a thermos flask.
2. The process should be very fast no effective heat exchange can take place in that very short time interval. Because of this reason expansion or compression of the gas should take place very fast. So adiabatic process is a very rapid process and any rapid thermal process is usually regarded as an adiabatic process.

We know that even good conduction is a relatively slow process. If we heat one end of a copper rod, the other end is not heated instantly. The heat takes some time to be conducted to the other end.

So a very rapid process is adiabatic even when the container is made of a conducting material. For this reason, a bicycle pump made of brass gets adiabatically heated due to very rapid pumping operations.

Relation between volume, pressure, and temperature of an Ideal gas in an adiabatic process: in an adiabatic process of an ideal gas, the relation pV = constant (Boyle’s law) is not obeyed, because the temperature is no longer a constant. Instead, the relation between volume and pressure becomes

pV^γ = constant ….(1)

where \(\gamma=\frac{C_p}{C_p}\) = constant for an ideal gas.

For n mol of an ideal gas, pV = nRT

So, \(p=\frac{n R T}{V} \text { and } V=\frac{n R T}{p}\)

Now, \(p V^\gamma= constant =A (say)\)

Then,  \(\frac{n R T}{V} V^\gamma=A\)

or, \(T V^{\gamma-1}=\frac{A}{n R}\)

i.e., \(T V^{\gamma-1}=\) constant ….(2)

Again, \(p\left(\frac{n R T}{p}\right)^\gamma=A or, T^\gamma p^{1-\gamma}=\frac{A}{(n R)^\gamma}\)

i.e., \(T^\gamma p^{1-\gamma}= constant\)….(3)

Relations (1) to (3) relate V, p, and T during an adiabatic process of an ideal gas.

Proof of equation pV^γ = constant: It has been shown that the first law of thermodynamics for a hydrostatic system can be written as

dQ = \(n C_\nu d T+p d V\)…(4)

Again for \(n \mathrm{~mol}\) of an ideal gas,

pV = nRT

or, pdV + Vdp = nRdT

or, \(d T=\frac{p d V+V d p}{n R}\)…(5)

For an adiabatic process, dQ = 0

∴ From equations (4) and (5) we get,

0 = \(n C_v\left(\frac{p d V+V d p}{n R}\right)+p d V\)

or, \(0=C_v V d p+(C_v+R) p d V\)

or, \(C_\nu V d p=-C_p p d V\) (because \(C_p-C_V=R\))

or, \(\frac{d p}{p}=-\frac{C_p}{C_v} \frac{d V}{V} or, \frac{d p}{p}+\gamma \frac{d V}{V}=0\) (because \(\gamma=\frac{C_p}{C_\nu}\))

∴ \(\int \frac{d p}{p}+\gamma \int \frac{d V}{V}=\text { constant }\)

or, \(\ln p+\gamma \ln V=\) constant

or, \(\ln p+\ln V^\gamma=\) constant

or, \(p V^\gamma=\) constant

Adiabatic process of an ideal gas on a pV- diagram: p V diagrams of adiabatic changes are called adiabatic curves. For a gas of particular mass, these curves are shown where S₁, S₂, and S₃ are the entropies of the gas.

The relation pV^γ = constant indicates that the adiabatic curves on a pV diagram will be different from the isothermal curves.

Calculations show that at every point on a pV diagram, the adiabatic curve has a greater slope. This means that the adiabatic curves are steeper than the isothermal curves.

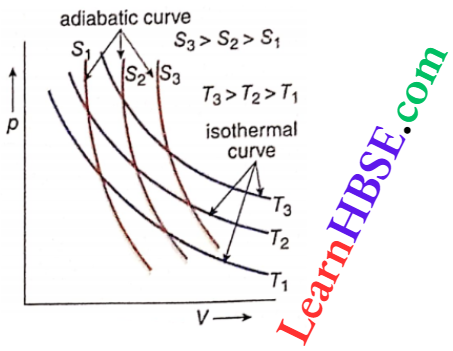
Two adiabatic curves cannot intersect because a point of intersection means two entropies of a gas, which is impossible. The slopes of an isothermal and an adiabatic curve on a pV-diagram are called isothermal slope and adiabatic slope, respectively.

Adiabatic and Isothermal Processes 

Relation between Isothermal and adiabatic slopes: For an isothermal change, pV = constant

Differentiating, pdV+ Vdp = 0

or, \(\frac{d p}{d V}=-\frac{p}{V}\) = slope of isothermal curve

For an adiabatic change, pV^γ = constant

Differentiating, \(\gamma p V^{\gamma-1} d V+V^\gamma d p=0\)

or, \(\frac{d p}{d V}=-\gamma \frac{p}{V}=\) = slope of adiabatic curve

So, adiabatic slope at a point = γ x isothermal slope at that point

As γ > 1, the adiabatic slope at every point is greater than the isothermal slope.

Work done by an ideal gas in an adiabatic process: The first law can be written (for all processes of an ideal gas) as

dQ = nC_vdT+ dW

Now, for an adiabatic process, dQ = O.

Then dW = -nC_vdT.

So for a change in temperature from T_i to T_f in an adiabatic process of an ideal gas, the total work done is,

W = \(\int d W=-n C_v \int_{T_i}^{T_f} d T=n C_v\left(T_i-T_f\right)\)

Again, \(\frac{R}{C_v}=\frac{C_p-C_v}{C_v}=\frac{C_p}{C_p}-1=\gamma-1\)

or, \(C_v=\frac{R}{\gamma-1}\)

So, \(W=\frac{n R}{\gamma-1}\left(T_i-T_f\right)\)…(7)

Again, \(p_i V_i=n R T_i$ and $p_f V_f=n R T_f\)

⊂ W = \(\frac{n R T_i-n R T_f}{\gamma-1}=\frac{p_i V_i-p_f V_f}{\gamma-1}\)

In relations (6) and (7), \(C_\nu and \frac{R}{\gamma-1}\) are positive quantities.

1. For an adiabatic expansion, W is positive. So T_i – T_f is positive, or T_f < T_i This means that the temperature decreases. This is adiabatic cooling. For this reason, the air coining out of a bursting bicycle or car tire appears to be cooler. This process is sometimes utilised to liquefy some gases.

2. For adiabatic compression, similar arguments show that the temperature increases. This is adiabatic heating. For this reason, a bicycle or football pump becomes hot during air compression due to pumping. However, adiabatic heating has no practical utilization.

Comparison between isothermal and adiabatic processes:

 Thermodynamics

First And Second Law Of Thermodynamics Isothermal And Adiabatic Process Numerical Examples

Example 1. 10 mol of an ideal gas is taken through an isothermal process in which the volume is compressed from 40 L to 30 L. If the temperature and the pressure of the gas are 0°C and 1 atm respectively, find the work done in the process. Given: R = 8.31 J · mol^-1 · K^-1.
Solution:

Given

10 mol of an ideal gas is taken through an isothermal process in which the volume is compressed from 40 L to 30 L. If the temperature and the pressure of the gas are 0°C and 1 atm respectively

R = 8.31 J · mol^-1 · K^-1

Work done for  n mole of gas, due to change in volume is an isothermal process,

W = \(n R T \ln \frac{V_f}{V_l}=n R T \times 2.3026 \log _{10} \frac{V_f}{V_l}\)

= \(10 \times 8.31 \times 273 \times 2.3026 \log _{10} \frac{30}{40}\)

= \(10 \times 8.31 \times 273 \times 2.3026 \log _{10} \frac{3}{4}\)

= \(10 \times 8.31 \times 273 \times 2.302610 .4771-0.6020]\)

= \(-10 \times 8.31 \times 273 \times 2.3026 \times 0.1251\)

The work done in the process= \(-6534.91 \mathrm{~J}\)

[the negative sign shows that work is done on the gas]

Adiabatic and Isothermal Processes 

Question 2. A gas has an initial volume of ll at a pressure of 8 atm. An adiabatic expansion takes the gas to a pressure of I atm. What will be its final volume? Given, γ = 1.5.
Solution:

Given

A gas has an initial volume of ll at a pressure of 8 atm. An adiabatic expansion takes the gas to a pressure of I atm.

⇒ \(p_1 V_1^\gamma=p_2 V_2^\gamma or, V_2^\gamma=V_1^\gamma \cdot \frac{p_1}{p_2}\)

Here, \(p_1=8 \mathrm{~atm}, V_1=1 \mathrm{l}, p_2=1 \mathrm{~atm}\)

∴ \(V_2=V_1\left(\frac{p_1}{p_2}\right)^{\frac{1}{\gamma}}=1 \times\left(\frac{8}{1}\right)^{\frac{2}{3}}\left[\gamma=1.5=\frac{3}{2}  \frac{1}{\gamma}=\frac{2}{3}\right]\)

= \(\left(2^3\right)^{\frac{2}{3}}=2^2=4 \mathrm{~L}\)

Example 3. Some amount of air, initially at STP, is adiabatically compressed to 1/5 th its initial volume. Determine the rise in temperature. Given, γ = 1.41.
Solution:

Given

Some amount of air, initially at STP, is adiabatically compressed to 1/5 th its initial volume.

In an adiabatic process, TVγ-1 = constant

or, \(T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1}\)

or, \(T_2=T_1\left(\frac{V_1}{V_2}\right)^{\gamma-1}\)

Here, \(T_1=0^{\circ} \mathrm{C}=273 \mathrm{~K}  \frac{V_1}{V_2}=5  \gamma-1=1.41-1=0.41\)

∴ \(T_2=273 \times(5)^{0.41}\)

= \(528.13 \mathrm{~K}=(528.13-273)^{\circ} \mathrm{C}=255.13^{\circ} \mathrm{C}\)

∴ Rise in temperature = \(255.13-0=255.13^{\circ} \mathrm{C}\).

Example 4. Some amount of gas at 27 °C is suddenly compressed to 8 times its initial pressure. If γ = 1.5, find out the rise in temperature.
Solution:

Given

Some amount of gas at 27 °C is suddenly compressed to 8 times its initial pressure. If γ = 1.5

As the gs is suddenly compressed, the process is adiabatic.

So, \(T_1^\gamma p_1{ }^{1-\gamma}=T_2^\gamma p_2{ }^{1-\gamma} or, \left(\frac{T_1}{T_2}\right)^\gamma=\left(\frac{p_2}{p_1}\right)^{1-\gamma} or, T_2=T_1\left(\frac{p_1}{p_2}\right)^{\frac{1-\gamma}{\gamma}}\)

Here, \(T_1=27^{\circ} \mathrm{C}=300 \mathrm{~K} ; \frac{p_2}{p_1}=8; \gamma=1.5=\frac{3}{2} or, 1-\gamma=1-\frac{3}{2}=-\frac{1}{2}\)

or, \(\frac{1-\gamma}{\gamma}=-\frac{1}{3}\)

∴ \(T_2=300 \times\left(\frac{1}{8}\right)^{-1 / 3}\)

= \(300 \times(8)^{1 / 3}\)

= \(300 \times 2=600 \mathrm{~K}\)

∴ Rise in temperature =600-300 =300 K = \(300^{\circ} \mathrm{C}\).

Adiabatic and Isothermal Processes 

Example 5. Find out the work done to expand an ideal gas isothermally to twice its initial volume.
Solution:

If 1 mol of an ideal gas is at a temperature T K

then, p V=R T or, \(p=\frac{R T}{V}\)

∴ Work done in isothermal process,

W = \(\int_{V_i}^{V_{f^{\prime}}} p d V=\int_{V_i}^{V_f} \frac{R T}{V} d V=R T \int_{V_i}^{V_f} \frac{d V}{V}=R T \ln \frac{V_f}{V_i}\)

[ T = constant in isothermal process]

Here,  \(\frac{V_f}{V_i}=2 \text { and } R=8.31 \mathrm{~J} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1}\)

W = \(8.31 \times T \times \ln 2=8.31 \times 0.693 T\)

= 5.76 T J

Example 6. Find out the work done in adiabatic compression of 1 mol of an ideal gas. The initial pressure and volume of the gas are 10⁵ N · m^-2 and 6 L respectively; the final volume is 2 L; the molar specific heat of the gas at constant volume is 3/2 R
Solution:

Here, \(C_v=\frac{3}{2} R\)

As \(C_p-C_v=R, C_p=C_v+R=\frac{3}{2} R+R=\frac{5}{2} R; so, \gamma=\frac{C_p}{C_v}=\frac{5}{3}\)

For 1 mol of the gas, \(p V=R T\) or, \(T=\frac{1}{R} p V\); the fall in temperature is \(T_i-T_f=\frac{1}{R}\left(p_i V_i-p_f V_f\right)\)

For this adiabatic process, \(p_i V_i^\gamma=p_f V_f^\gamma\)

or, \(p_f=p\left(\frac{V_f}{V_f}\right)^\gamma=10^5 \times\left(\frac{5}{2}\right)^{5 / 3}=6.24 \times 10^5 \mathrm{~N} \cdot \mathrm{m}^{-2}\)

∴  Work done, W = \(\frac{R}{\gamma-1}\left(T_i-T_f\right)=\frac{R}{7-1} \cdot \frac{1}{R}\left(p_i V_i-p_f V_f\right)\)

= \(\frac{p_i V_i-p_f V_f}{\gamma-1}\)

= \(\frac{10^5 \times 6 \times 10^{-3}-6.24 \times 10^5 \times 2 \times 10^{-3}}{\frac{5}{3}-1}\)

= \(\frac{3}{2} \times\left(6 \times 10^2-6.24 \times 2 \times 10^2\right) \quad\left[1 \mathrm{~L}=10^{-3} \mathrm{~m}^3\right]\)

= \(\frac{3}{2} \times 10^2 \times(6-12.48)=-\frac{3}{2} \times 10^2 \times 6.48\)

=-972 J.

Adiabatic and Isothermal Processes 

Example 7. The molar specific heat of an Ideal gas at constant pressure is C_p = 5/2 R. Some amount of this gas in a closed container has a volume of 0.0083 m³, a temperature 300 K, and a pressure 1.6 x 10⁶ N · m^-2. if 2.49 x 10⁴ J of heat is supplied at a constant volume of the gas, find out the final temperature and pressure. Given, R = 8.3 J · mol^-1 · K^-1
Solution:

Given

The molar specific heat of an Ideal gas at constant pressure is C_p = 5/2 R. Some amount of this gas in a closed container has a volume of 0.0083 m³, a temperature 300 K, and a pressure 1.6 x 10⁶ N · m^-2. if 2.49 x 10⁴ J of heat is supplied at a constant volume of the gas,

Let n mol of the gas be present in the container.

∴ p V=n R T

or, n =\(\frac{p V}{R T}\)

= \(\frac{\left(1.6 \times 10^6\right) \times 0.0083}{8.3 \times 300}=5.33\)

Now, \(C_y  =C_p-R=\frac{5}{2} R-R=\frac{3}{2} R\)

= \(1.5 \times 8.3 \mathrm{~J} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1}\)

Heat supplied at constant volume, \(Q_v=n C_v\left(T_f-T_i\right)\)

or, \(T_f-T_i=\frac{Q_v}{n C_v}=\frac{2.49 \times 10^4}{5.33 \times(1.5 \times 8.3)}=375.2 \mathrm{~K}\)

or, \(T_f=T_i+375.2=300+375.2=675.2 \mathrm{~K}\)

∴ Final temperature is 675.2 K

At constant volume, \(\frac{p_i}{T_i} \neq \frac{p_f}{T_f}\)

or, \(p_f=p_i \frac{T_f}{T_i}=\left(1.6 \times 10^6\right) \times \frac{675.2}{300}\)

= \(3.6 \times 10^6 \mathrm{~N} \cdot \mathrm{m}^{-2}\)

∴ Final pressure is 3.6 x 10⁶ N m^-2

Example 8. 8 g oxygon, 14 g nitrogen, and 22 g carbon dioxide arc mixed in a container of volume 4 1. Find out the pressure of the gas mixture at 27°C. Given, R = 8.315 j • mol^-1 • K^-1.
Solution:

Given

8 g oxygon, 14 g nitrogen, and 22 g carbon dioxide arc mixed in a container of volume 4 1.

If n = number of moles in a gas, then pV = nRT.

So, p = \(\frac{n R T}{V}=\frac{m}{M} \frac{R T}{V}\), where m = mass of the gas and M = molecular weight.

Then the pressures due to oxygen, nitrogen, and carbon dioxide gases,  respectively, are

∴ \(p_1=\frac{8}{32} \frac{R T}{V}, p_2=\frac{14}{28} \frac{R T}{V}, p_3=\frac{22}{44} \frac{R T}{V}\)

∴ Net pressure of the gas mixture is

p = p₁ + p₂ + p₃

= \(\left(\frac{8}{32}+\frac{14}{28}+\frac{22}{44}\right) \frac{R T}{V}=\left(\frac{1}{4}+\frac{1}{2}+\frac{1}{2}\right) \frac{R T}{V}=\frac{5}{4} \frac{R T}{V}\)

= \(\frac{5}{4} \times \frac{8.315 \times 300}{4 \times 10^{-3}}\)

(Here, \(T=27^{\circ} \mathrm{C}=300 \mathrm{~K}, V=41=4 \times 10^{-3} \mathrm{~m}^3\))

= \(7.795 \times 10^5 \mathrm{~N} \cdot \mathrm{m}^{-2}\)