Class 11 Physics Kinetic Theory Of Gases Question and Answers

Kinetic Theory Of Gases

Question 1. Which one of the following is not true for an ideal gas?

1. The molecules of an ideal gas move randomly
2. The molecules of an ideal gas attract one another
3. The volume of the molecules of an ideal gas is negligible
4. The pressure of an ideal gas increases with an increase in the velocity of its molecules

Answer: 2. The molecules of an ideal gas attract one another is correct

Question 2. A monatomic ideal gas is heated at constant pressure. How much fraction of heat is used to increase internal energy?

1. 2/5
2. 3/5
3. 3/7
4. 3/4

Answer:

If ΔT is the increase in temperature of a monoatomic ideal gas, increase in internal energy, \(\Delta E=\frac{3}{2} R \Delta T\) [for 1 mol gas]

Again, molar specific heat at constant pressure, \(C_p=\frac{5}{2} R\).

So, given heat to increase the temperature by ΔT at constant pressure = \(C_p \Delta T=\frac{5}{2} R \Delta T\)

Hence, the required fraction

= \(\frac{\text { increase in internal energy }}{\text { given heat }}=\frac{\frac{3}{2} R \Delta T}{\frac{5}{2} R \Delta T}=\frac{3}{5}\)

The option 2 is correct.

Kinetic Theory Of Gases Class 11 Notes

Question 3. Kinetic theory proves that, the pressure of a gas p = \(\frac{2 E}{3 v}\)(where v = 1 molar volume, E = kinetic = energy).
Answer:

Given

The pressure of a gas p = \(\frac{2 E}{3 v}\)(where v = 1 molar volume, E = kinetic = energy)

Molar mass of the gas = M;

Number of molecules = Avogadro’s number = N;

Molar volume of the gas = v = \(\frac{M}{\rho} \text {. }\)

We know, pressure, \(p=\frac{1}{3} \rho c^2\)

Here, ρ = density of the gas,

c = rms speed of gas molecules

Now, the kinetic energy of the gas molecules,

E = \(\frac{1}{2} m c_1^2+\frac{1}{2} m c_2^2+\cdots+\frac{1}{2} m c_N^2\)

= \(\frac{1}{2} m N \frac{c_1^2+c_2^2+\cdots+c_N^2}{N}\)

= \(\frac{1}{2} M c^2=\frac{1}{2} M \cdot \frac{3 p}{\rho}=\frac{3}{2} p v\)

Hence, \(p=\frac{2 E}{3 v}\)

Kinetic Theory Of Gases Class 11 Numericals

Question 4. In thermal equilibrium, the rms velocity of a gas molecule is

1. Proportional to T²
2. Proportional to T²
3. Proportional to √T
4. Zero

Answer:

rms speed of gas molecule, = \(\sqrt{\frac{3 R T}{M}}\)

The option 3 is corrections

Question 5. Write the expression for mean free path
Answer:

The expression for mean free path

Mean free path, \(\lambda=\frac{1}{\pi \sigma^2 n}\)

where n = number of molecules in unit volume;

= diameter of each gas molecule.

Question 6. From fonetic theory of gases proves that the pressure of 1 a gas p = 2E/3V, where V = 1 molar volume, E = Kinetic energy.
Answer:

Given

Molar mass of the gas =M, Number of molecules = Avogadro number = N,

Molar volume = V = \(\frac{M}{\rho}\), pressure = p = \(\frac{1}{3} \rho c^2\), here = density of gas, c= rms speed.

Kinetic energy of gas molecules, E

= \(\frac{1}{2} m c_1^2+\frac{1}{2} m c_2^2+\cdots+\frac{1}{2} m c_N^2\)

= \(\frac{1}{2} m N \frac{c_1^2+c_2^2+\cdots+c_N^2}{N}=\frac{1}{2} M c^2=\frac{1}{2} M \cdot \frac{3 p}{c}=\frac{3}{2} p V\)

Therefore, \(p=\frac{2 E}{3 V}\)

Question 7. The volume and pressure of two moles of an ideal gas are V and p respectively Another 1 mol ideal gas haring volume 2V also exerts the same pressure p. Molecular mass of the second gas is 16 times that of the first gas. Compare the rms velocities of the two gases.
Answer:

Given

The volume and pressure of two moles of an ideal gas are V and p respectively Another 1 mol ideal gas haring volume 2V also exerts the same pressure p. Molecular mass of the second gas is 16 times that of the first gas.

If the temperature of the first gas is \(T_1\), then \(p V=2 R T_1\) and the temperature of the second gas \(T_2\), then P.

then \(P \cdot 2 \mathrm{~V}=R T_2 or, p \mathrm{~V}=\frac{1}{2} R T_2\)

According to the question, \(2 R T_1=\frac{1}{2} R T_2 \quad \text { or } \frac{T_1}{T_2}=\frac{1}{4} \)

rms speed, c = \(\sqrt{\frac{3 R T}{M}}\)

∴ \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2} \cdot \frac{M_2}{M_1}}=\sqrt{\frac{1}{4} \times \frac{16}{1}}=\frac{2}{1}\)

or, \(c_1=2 c_2\)

Kinetic Theory Of Gases Class 11 Important Questions

Question 8. The perfect equation for 4g ofhydroÿst gas is

1. pV = RT
2. pV = 2RT
3. pV = 1/2 RT
4. pV = 4RT

Answer:

The number of moles in 4 g of hydrogen gas.

n = \(\frac{m}{M}=\frac{4}{2}=2 \mathrm{~mol}\)

∴ perfect equation, pV = nRT

on pV=2RT

The option 2 is correct.

Question 9. The relation \(p=\frac{1}{3} m n c_{m s}^2\), shows that the mean kinetic energy of a molecule is the same for all types of gases.
Answer:

Given, \(p=\frac{1}{3} m n c_{\text {rms }}^2=\frac{1}{3} \frac{m N}{V} c_{\text {rms }}^2\)

[N= number of molecules, V= volume]

or, \(\frac{1}{3} m c_{\mathrm{mms}}^2=\frac{p V}{N}=\frac{\left(\frac{N}{N_n}\right) R T}{N}\)

(\(N_A\)= Avogadro’s number)

or \(\frac{1}{2} m c_{\mathrm{rms}}^2=\frac{3 R T}{2} \frac{R}{N_A}\)

∴ mean kinetic energy of a molecule = \(\frac{1}{2} m c_{\text {rms }}^2=\frac{3 R T}{2} \frac{R T}{N_A}\)

Is the same for all types of gases at a particular temperature.

Kinetic Theory Of Gases Class 11 Derivations

Question 10. The rms speed of oxygen is v at a particular temperature. If the temperature is doubled and oxygen molecules dissociate Into oxygen atoms, the rms speed becomes

1. v
2. √2v
3. 2v
4. 4v

Answer:

The rms speed of oxygen molecule, v = \(\sqrt{\frac{2 R T}{M}}\)

When the molecules dissociate into oxygen atoms, molar mass will change from M to M/2 (when the temperature changes from T to 2 T)

Then, rms speed = \(\sqrt{\frac{3 R \cdot 2 T}{M / 2}}=2 \sqrt{\frac{3 R T}{M}}=2 v\)

The option 3 is correct.

Question 11. If the rms velocity of hydrogen gas at a certain temperature is c, then the rms velocity of oxygen gas at the same temperature is

1. \(\frac{c}{8}\)
2. \(\frac{c}{10}\)
3. \(\frac{c}{4}\)
4. \(\frac{c}{2}\)

Answer:

rms velocity of hydrogen gas, c = \(\sqrt{\frac{3 R T}{2}}\)

rms velocity of oxygen gas, \(c_{\mathrm{O}_2}=\sqrt{\frac{3 R T}{32}}\)

∴ \(c_{\mathrm{O}_2}=\sqrt{\frac{2}{32}} \times c=\frac{c}{4}\)

The option 3 is correct.

Question 12. The temperature of an ideal gas, initially at 27°C, is raised by 6°C. The rms velocity of the gas molecule will,

1. Increase by nearly 2%
2. Decrease by nearly 2%
3. Increase by nearly 1%
4. Decrease by nearly 1%

Answer:

⇒\(\nu_{\mathrm{rms}} \propto \sqrt{T}\)

or, \(\frac{\Delta \nu}{\nu}=\frac{1}{2} \frac{\Delta T}{T}=\frac{1}{2} \times \frac{6}{(273+27)}=\frac{1}{100}=1 \%\)

The option 3 is correct

Question 13. An open pipe made up of glass is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by an additional 46 cm. What will be the length of the air column above the mercury in the tube now? (atm pressure = 76 cm of Hg)

1. 16 cm
2. 22 cm
3. 38 cm
4. 6 cm

Answer:

Let <α = cross-sectional area of the pipe (in cm²)

So, initially, the volume of air above mercury, V₁ = 8α cm³; pressure, p₁ = 76 cm Hg.

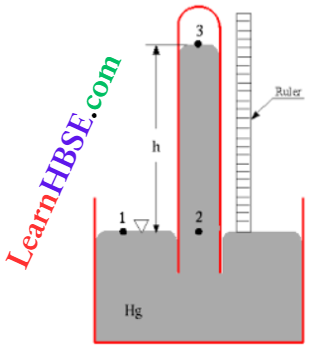
When the top of the pipe is (46 + 8) or 54 cm higher than the outer mercury level, let x = rise of mercury level inside the pipe.

Then, the volume of air inside the pipe, v₂ = (54 – x)a cm³

and its pressure, p₂ = (76 – x) cm Hg

From Boyle law, p₁V₁ = p₂V₂

or, 76 x 8a = (76 – x)(54 – x)a

or, 608 = 4104- 130x+ x²

or, x² – 130x + 3496 = 0

or, (x-38)(x-92) = 0;

So, x = 38 cm or, x = 92 cm

The only physically meaningful solution is x = 38 cm Therefore, the length of the air column in the pipe above mercury =54-38 = 16 cm

The option 1 is correct.

Question 14. Consider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion, the average time of collision between molecules increases as V^q, where V is the volume of the gas. The value of q is  \(\left(\gamma=\frac{C_p}{C_\nu}\right)\)

1. \(\frac{3 \gamma+5}{6}\)
2. \(\frac{3 \gamma-5}{6}\)
3. \(\frac{\gamma+1}{2}\)
4. \(\frac{\gamma-1}{2}\)

Answer:

The rms speed of the molecules, c = \(\sqrt{3 R T / M}\)

Mean free path, \(\lambda=\frac{1}{\sigma^2 n}=\frac{1}{\sigma^2 \frac{N}{\nu}}\)

[N = number of molecules, cr = diameter of the molecules]

Average time of collision between the molecules,

t = \(\frac{\lambda}{c}=\frac{V}{\sigma^2 N} \frac{1}{\sqrt{3 R T / M}}\)

or, \(t \propto \frac{V}{\sqrt{T}}\)

or, \(T \propto \frac{V^2}{t^2}\)

Again, in the adiabatic process, \(T V^{\gamma-1}=\text { constant } \quad \text { or, } T \propto V^{1-\gamma}\)

∴ \(\frac{V^2}{t^2} \propto V^{1-r}\)

or, \(t^2 \propto v^{\gamma+1}\) or, \(t \propto V^{\frac{\gamma+1}{2}}\)

Hence, \(q=\frac{\gamma+1}{2}\)

The option 3 is correct

Kinetic Theory Of Gases Formula Class 11

Question 15. An ideal gas undergoes a quasistatic, reversible process in which its molar heat capacity C remains constant. If during this process the relation of pressure p and volume V is given by pVⁿ = constant, then n is given by (here C_p and C_v are molar specific heat at constant pressure and constant volume, respectively)

1. n = \(\frac{C_p}{C_\nu}\)
2. n = \(\frac{C-C_p}{C-C_\nu}\)
3. n = \(\frac{C_p-C}{C-C_\nu}\)
4. n = \(\frac{C-C_\nu}{C-C_p}\)

Answer:

Here, \(p V^n=k\) (constant)….(1)

For \(1 \mathrm{~mol}\) of ideal gas,

pV = RT…(2)

Dividing (1) by (2) we get, \(V^{n-1} T=\frac{k}{R}\)

∴ \(\left(\frac{d V}{d T}\right)=\frac{V}{(n-1) T}=\frac{V}{(1-n) T}\)

According to first law of thermodynamics,

dQ = \(C_\nu d T+p d V\)

∴ \(\frac{d Q}{d T}=C_\nu+p\left(\frac{d V}{d T}\right)=C_\nu+\frac{p V}{(1-n) T}=C_\nu+\frac{R}{1-n}\)

Hence, thermal capacity, \(C=C_\nu+\frac{R}{1-n}\)

or, \(1-n=\frac{R}{C-C_v}\)

or, \(n=1-\frac{R}{C-C_\nu}=\frac{C-\left(C_\nu+R\right)}{C-C_\nu}=\frac{C-C_p}{C-C_\nu}\)

(because \(C_p-C_v=R\))

The option 2 is correct.

Question 16. The mean free path of a molecule of gas (radius r) is inversely proportional to

1. r³
2. r²
3. r
4. √r

Answer:

Mean free path,

λ = \(\frac{1}{\sqrt{2} \pi d^2 n}=\frac{1 \times 4}{\sqrt{2} \pi r^2 n}\)

∴ \(\lambda \propto \frac{1}{r^2}\)

The option 2 is correct

Question 17. The ratio of the specific heats \(\frac{C_p}{C_v}=\gamma\) in terms of degrees of freedom (n) is given by

1. \(\left(1+\frac{1}{n}\right)\)
2. \(\left(1+\frac{n}{3}\right)\)
3. \(\left(1+\frac{2}{n}\right)\)
4. \(\left(1+\frac{n}{2}\right)\)

Answer:

⇒ \(C_\nu=\frac{n}{2} R, C_P=\frac{n}{2} R+R=\frac{n+2}{2} R\)

∴ \(\gamma=\frac{\frac{n+2}{2} R}{\frac{n}{2} R}=\frac{n+2}{n}=1+\frac{2}{n}\)

The option 3 is correct.

Question 18. The molecules of a given mass of a gas have rms velocity of 200 m · s^-1 at 27 °C and 1.0 x 10⁵ N · m^-2 pressure. When the temperature and pressure of the gas are respectively, 127 °C and 0.05 x 10⁵ N · m^-2, the rms velocity of its molecules in m · s^-1 is

1. \(\frac{400}{\sqrt{3}}\)
2. \(\frac{100 \sqrt{2}}{3}\)
3. \(\frac{100}{3}\)
4. \(100 \sqrt{2}\)

Answer:

rms speed of gas molecule, c ∝ √T

∴ \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}=\sqrt{\frac{27+273}{127+273}}=\sqrt{\frac{300}{400}}=\frac{\sqrt{3}}{2}\)

or, \(c_2=\frac{2}{\sqrt{3}} c_1=\frac{2}{\sqrt{3}} \times 200=\frac{400}{\sqrt{3}} \mathrm{~m} / \mathrm{s}\)

The option 1 is correct.

Kinetic Theory Of Gases Assumptions Class 11

Question 19. When the temperature of a gas is raised from 30°C to 90°C, the percentage Increase in the rms velocity of the molecules will be

1. 60%
2. 10%
3. 15%
4. 30%

Answer:

30°C = 303K, 90°C = 363K

rms speed, \(c \propto \sqrt{T}\)

Hence, \(\frac{c_2}{c_1}=\sqrt{\frac{T_2}{T_1}}=\sqrt{\frac{363}{303}}=\sqrt{1.2} \approx 1.1\)

∴ The percentage increase

= \(\frac{c_2-c_1}{c_1} \times 100=\left(\frac{c_2}{c_1}-1\right) \times 100\)

= \((1.1-1) \times 100=10 \%\)

The option 2 is correct.

Question 20. At what temperature will the rms speed of oxygen molecules become just sufficient for escaping from the earth’s atmosphere? [Given: Mass of oxygen molecule (m) = 2.76 x 10^-26 kg Boltzmann’s constant k =
1.38 x 10^-23 J • K^-1]

1. 5.016 X10⁴ K
2. 8.360 x 10⁴ K
3. 2.508 x 10⁴K
4. 1.254 x 10⁴ K

Answer:

Escape velocity of a body for the earth, \(v_e=\sqrt{2 g R}=\sqrt{2 \times 9.8 \times 6400 \times 10^3}\)

= 11200 m/s

Let us consider, at temperature TK, the escape velocity of the oxygen molecules will be (v_e).

Then, \(\sqrt{\frac{3 k_B T}{m}}=v_e\)

or, \(\frac{3 \times 1.38 \times 10^{-23}}{2.76 \times 10^{-26}} \cdot T=(11200)^2\)

or, T = \(8.363 \times 10^4 \mathrm{~K}\)

The option 2 is correct.

Question 21. What would be the effect on the rms speed of gas molecules if the temperature of the gas is increased by a factor of 4?
Answer:

We know, rms speed, c = \(\sqrt{\frac{3 R T}{M}}\)

∴ \(c \propto \sqrt{T}\)

Now, \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}=\sqrt{\frac{T_1}{4 T_1}}=\frac{1}{2}\)

(since \(T_2=4 T_1\))

or, \(\quad c_2=2 c_1\)

So, rms speed is doubled

Question 22. A flask contains Argon and Chlorine in the ratio of 2:1 by mass. The temperature of the mixture is 27°C. Obtain the ratio of average kinetic energy per molecule and root mean square speed v_rms of the molecules of the two gases. Given: atomic mass of argon =39,9 U and molecular mass of chlorine = 70.9 u.
Answer:

Given

A flask contains Argon and Chlorine in the ratio of 2:1 by mass. The temperature of the mixture is 27°C.

atomic mass of argon =39,9 U and molecular mass of chlorine = 70.9 u

Average kinetic energy of a molecule of any ideal gas = \(\frac{3}{2}\)kT

1. As both argon and chlorine have the same temperature, the ratio of average kinetic energy per molecule of the two gases =1:1

2. Let m be the mass of a molecule of the gas.

Now, average kinetic energy per molecule = \(\frac{1}{2} m v_{\mathrm{rms}}^2\)

∴ \(\frac{1}{2} m_1 v_1^2=\frac{1}{2} m_2 v_2^2=\frac{3}{2} k T\)

or, \(\frac{v_1^2}{v_2^2}=\frac{m_2}{m_1}=\frac{M_2}{M_1}=\frac{70.9}{39.9}=1.7\)

where M is the atomic or molecular mass of the gas.

So, \(\frac{v_1}{v_2}=\sqrt{1.77}=1.33\)

Here, the composition of a mixture of gases is not relevant since,

⇒ \(\frac{v_1}{v_2}=\sqrt{\frac{\overline{M_2}}{M_1}}=\text { constant }\)

Question 23. Prove that the average kinetic energy of a molecule of an ideal gas is directly proportional to the absolute temperature of the gas.
Solution:

We know that the average kinetic energy of a molecule is directly proportional to the absolute temperature of the gas.

Let one gram mole of an ideal gas occupy a volume V at temperature T.

If m is the mass of each molecule of the gas, then M = m x N_A [where N_A is the Avogadro’s number]

If c is the rms speed of the gas molecules, then the pressure exerted by the ideal gas is p = \(\frac{1}{3} \rho c^2=\frac{1}{3} \frac{M}{V} c^2\)

Now from the equation pV = RT,

⇒ \(\frac{1}{3} M c^2=R T \quad or, M c^2=3 R T \quad or, [latex]\frac{1}{2} M c^2=\frac{3}{2} R T\)

or, \(\frac{1}{2} m N_A c^2=\frac{3}{2} R T \quad\left[because M=m N_A\right]\)

or, \(\frac{1}{2} m c^2=\frac{3}{2}\left(\frac{R}{N_A}\right) T=\frac{3}{2} k_B T\left[because k_B=\frac{R}{N_A}\right]\)

So, the average kinetic energy of translation per molecule of a gas

= \(\frac{1}{2} m c^2=\frac{3}{2} k_B T\)

Hence, the average kinetic energy of a molecule is directly proportional to the absolute temperature of the gas.

Question 24. The absolute temperature of a gas is increased 3 times. What will be the increase in root mean square velocity of the gas molecule?
Answer:

Given

The absolute temperature of a gas is increased 3 times.

rms velocity in terms of Boltzmann constant (k),

c = \(\sqrt{\frac{3 k T}{m}}\)

At temperature, \(T_1, c=\sqrt{\frac{3 k T_1}{m}}\)

Now, \(T_2=3 T_1\)

∴ \(c_2=\sqrt{\frac{3 k T_2}{m}}=\sqrt{\frac{3 k \times 3 T_1}{m}}=\sqrt{3} \cdot \frac{\sqrt{3 k T_1}}{m}\)

or, \(c_2=\sqrt{3} c\)

If the temperature of the gas increases 3 times, then the root mean square velocity of the gas particles increases by a factor of √3.