Class 11 Physics Work And Energy Questions And Answers

Work And Energy Questions And Answers

In this type, the answer to each of the questions is a single-digit integer ranging from 0 to 9.

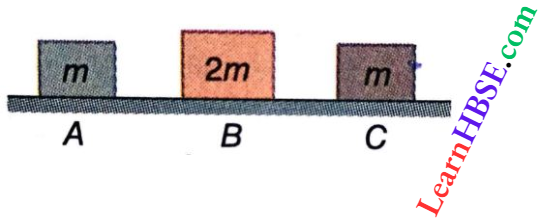
Question 1. Three objects A, B, and C are kept in a straight line on a frictionless horizontal surface. These have masses m, 2 m, and m respectively. The object A moves towards B with a speed of 9 m · s^-1 and makes an elastic collision with it. Thereafter, B makes a completely inelastic collision with C. All motions occur in the same straight line. Find the final speed (in m · s^-1) of the object C.
Answer: 4

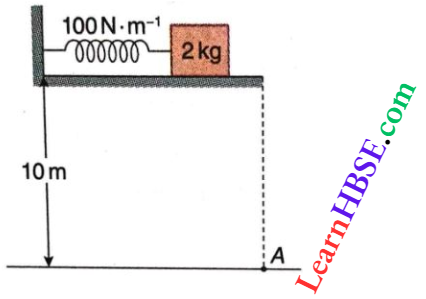
Question 2. A block of mass 2kg is compressed against a spring of spring constant 100 N m^-1 such that the compression in the spring is 20 cm. From here the block is released from rest as shown. Determine the distance (in meters) from A where the block falls. [Take g = 10 m · s^-2]
Answer: 2

Wave Motion Class 11 Physics Notes

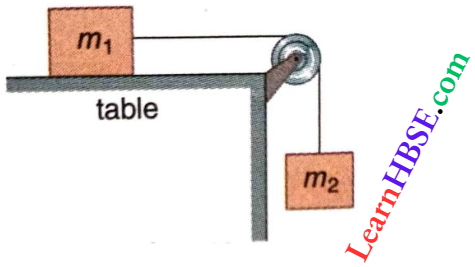
Question 3. Two blocks having masses m₁ = 10 kg and m₂ = 5 kg are connected by an ideal string as shown. The coefficient of friction between m₁ and the surface is μ = 0.2. Assuming that the system is released from rest, calculate the .velocity (in m • s^-1) of the blocks when m₂ has descended by 4m. [Take g = 10 m • s^-2]
Answer: 4

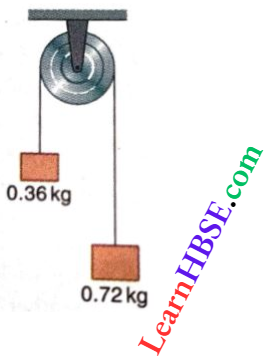
Question 4. A light inextensible string that goes over a smooth fixed pulley, as shown, connects two blocks of masses 0.36 kg and 0.72 kg. Taking g = 10m · s^-2, find the work done (in joules) by the string on the block of mass 0.36 kg during the first second after the system is released from rest.
Answer: 8

Wave Motion Class 11 Pdf Download

Question 5. A body of mass 4 kg’ is moving with a momentum of 8 kg · m · s^-1. A force of 0.4 N acts on it in the direction of motion of the body for 10 seconds. Determine the increase in kinetic energy in joules.
Answer: 9

Work And Energy Short Answer Type Questions

Question 1. The velocity of a 10 kg mass is increased from 2 m · s^-1 to 4 m · s^-1. The amount of work done in doing so is

1. 60 J
2. 20 J
3. 120 J
4. Cannot be determined from the given data

Answer:

Amount of work

= \(\frac{1}{2} m\left(v_f^2-v_i^2\right)=\frac{1}{2} \times 5 \times\left(4^2-2^2\right)=60 \mathrm{~J}\)

The option 1 is correct.

Question 2. When a spring is stretched by an amount of 3 cm, the potential energy stored in the spring is U. If the spring is stretched by an amount of 6 cm its stored potential energy is

1. 2U
2. 3 U
3. 4U
4. 6U

Answer:

Stored energy = U x \(\frac{6^2}{3^2}\) = 4 U

The option 3 is correct.

Numerical Problems On Wave Motion Class 11

Question 3. A car of mass M moves up an inclined road making an angle 6 with the horizontal with constant speed v. If H is the coefficient of friction between the tyre of the car and the road, show that the power of the engine of the car is P = vMg(sinθ + μcosθ).
Answer:

Given

A car of mass M moves up an inclined road making an angle 6 with the horizontal with constant speed v. If H is the coefficient of friction between the tyre of the car and the road,

The upward acceleration along the inclined plane, a = g(sinθ + μcosθ)

Now the upward force acting on the car, F = Ma

Hence, the power of the car engine,

P = Fv = vMg(sinθ + μcosθ)

Question 4. A particle moves from a point \(\vec{r}_1=\hat{i}+3 \hat{j}\) in meter to another point \(\vec{r}_2=2\hat{i}+4\hat{j}\) in meter under the action of the force \(\vec{F}=3\hat{i}+5\hat{j}\) in newton. Find the work done by the force on the particle during the displacement.
Answer:

Displacement, \(\vec{s}=\vec{r}_2-\vec{r}_1=(2 \hat{i}+4 \hat{j})-(\hat{i}+3 \hat{j})=(\hat{i}+\hat{j}) \mathrm{m}\)

Thus, work done, \(W=\vec{F} \cdot \vec{s}=(3 \hat{i}+5 \hat{j}) \cdot(\hat{i}+\hat{j})=3+5=8 \mathrm{~J}\)

Question 5. A box is being displaced by a machine of fixed power along a straight line. The displacement is time t is proportional to

1. \(t^{1 / 2}\)
2. \(t^{3 / 4}\)
3. \(t^{3 / 2}\)
4. \(t^2\)

Answer:

At t = 0, let velocity and displacement be zero.

Now when v = 0 and s = 0, C = 0 and C’ = 0

In that case, s = \(\frac{2 \sqrt{2}}{3} \sqrt{\frac{p}{m}}(t+0)+0=\frac{2}{3} \sqrt{\frac{2 p}{M}} t^{3 / 2} \quad \text { or, } s \propto t^{3 / 2}\)

The option 4 is correct.

Wave Motion Class 11 NCERT Solutions

Question 6. Two springs having force constant k₁ and k₂( k₁ > k₂) respectively increase their length by the same amount. On which spring work will be more and why?
Answer:

Given

Two springs having force constant k₁ and k₂( k₁ > k₂) respectively increase their length by the same amount.

Let the increase in length of each spring be x.

So the work done on the first spring, \(W_1=\frac{1}{2} k_1 x^2\)

and work done on the second spring, \(W_2=\frac{1}{2} k_2 x^2\)

∴ \(\frac{W_1}{W_2}=\frac{k_1}{k_2}\) (because \(k_1>k_2\)(given))

Hence, more work will be done on the first spring.

Question 7. The velocity of a moving body of mass m along positive. x axis is v = a√x (a = constant). Find the work done by the force applied on the body to displace it from x = 0 to x = l.
Answer:

Given

The velocity of a moving body of mass m along positive. x axis is v = a√x (a = constant)

Power, P = Fv = mfv = mv\(\frac{dv}{dt}\)

(acceleration of the body =\(\frac{dv}{dt}\))

So, work done,

W = \(\int p d t=m \int v d v=\frac{m v^2}{2}+c=\frac{m a^2 x}{2}+c\)

[c = integration constant]

At x = 0 , W = 0

∴ c = 0

Now when x = l, W = \(\frac{1}{2}\)ma²l

Wave Motion Examples Class 11

Question 8. If the coefficient of restitution is zero for collision between two bodies then

1. Both the bodies are at rest
2. Both are attached with each other
3. Both are moving with the same velocity in the opposite directions
4. Both are moving in the same direction with different velocities

Answer:

The option 2 is correct.

Question 9. 1 joule = 1 _______

1. N · ²
2. kg · m · s^-2
3. N · m
4. N² · m²

Answer:

Work done = applied force x displacement

The option 3 is correct.

Question 10. Prove that for perfect elastic collisions of two bodies moving in the same line, the kinetic energy is conserved.
Answer:

Suppose m₁ and m₂ are the masses of two particles which are moving with velocities u₁ and u₂ respectively (u₁> u₂) in the same direction along a straight line. They collide elastically, and after collision, move along the same direction with velocities v₁ and v₂ respectively.

So, the coefficient of restitution, e = \(\frac{v_2-v_1}{u_1-u_2}\)

For elastic collision, e = 1

or, \(v_2-v_1=u_1-u_2\)

or, \(u_1+v_1=u_2+v_2\)…(1)

As no external force is applied on the system, from the law of conservation of momentum,

total momentum before collision = total momentum after collision

or, \(m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2\)

or, \(m_1\left(v_1-u_1\right)=m_2\left(u_2-v_2\right)\)….(2)

Multiplying equations (1) and (2), \(m_1\left(v_1^2-u_1^2\right)=m_2\left(u_2^2-v_2^2\right)\)

or, \(\frac{1}{2} m_1\left(v_1^2-u_1^2\right)=\frac{1}{2} m_2\left(u_2^2-v_2^2\right)\)

or \(\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2=\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2\)

Kinetic energy after collision = kinetic energy before collision.

Progressive And Stationary Waves Class 11

Question 11. Define the gravitational unit of work done.
Answer:

The gravitational unit of work done

In SI, the gravitational unit of work done is kg • m.

Question 12.

1. Draw the graph representing linear momentum and change in kinetic energy.
2. A particle of mass m is rotated in a circular path of radius r under the influence of a force F = –\(\frac{k}{r ^2}\) where k is a constant. Find the total energy of the particle.

Answer:

1. Linear momentum of a particle of mass m, p = \(\sqrt{2 m K}\)

[where K is kinetic energy of the particle]

∴ p ∝ √K

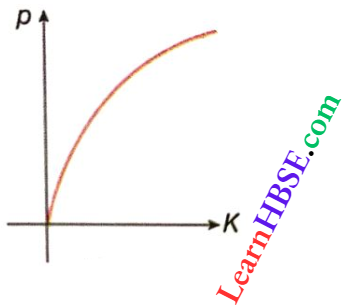
2. \(\frac{m v^2}{r}=\frac{k}{r^2}\)

Kinetic energy = \(\frac{1}{2} m v^2=\frac{1}{2} \cdot \frac{k r}{r^2}=\frac{k}{2 r}\)

Potential energy = \(-\int_{\infty}^r F \cdot d r=k \int_{\infty}^r \frac{d r}{r^2}=-\frac{k}{r}\)

∴ Total energy = \(\frac{k}{2 r}-\frac{k}{r}=-\frac{k}{2 r}\)

Transverse And Longitudinal Waves Class 11

Question 13. Which of the following is not conserved in an inelastic collision?

1. Momentum
2. Kinetic energy
3. Both momentum and KE
4. None of these

Answer:

Kinetic energy is not conserved in inelastic collision.

The option 2 is correct.

Question 14. A stone tied to a string of length L is whirled in a vertical circle with the other end of the string at the center. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of its velocity, as it reaches a position where the string is horizontal, is

1. \(\sqrt{u^2-2 g L}\)
2. \(\sqrt{2 g L}\)
3. \(\sqrt{u^2-g L}\)
4. \(\sqrt{2\left(u^2-g L\right)}\)

Answer:

Let the mass of the stone is m.

At the lowest point of the circular path, the potential energy of the stone = 0 and kinetic energy = \(\frac{1}{2}\)mu³

When the string is horizontal, the stone is at a height L from its lowest point.

Hence, potential energy = mgL

and kinetic energy = \(\frac{1}{2}\)mv²

[v = velocity of the stone at L]

From the law of conservation of energy, we get, \(0+\frac{1}{2} m u^2=m g L+\frac{1}{2} m v^2\)

or, \(v^2=u^2-2 g L \quad \text { or, } v=\sqrt{u^2-2 g L}\)

The option 1 is correct.

Question 15. The number of joules in 1 kg· m is

1. 9.8
2. 980
3. 1000
4. 10⁵

Answer:

1 kg · m = 1 kgf x 1 m = 9.8 N x 1 m = 9.8 J

The option 1 is correct.

Question 16. The displacement of a body of mass 3 kg under the action of a force is s = \(\frac{t^2}{s}\) meter. The work done in time 2s by the same force (in J) is

1. 2
2. 3.8
3. 5.2
4. 2.66

Answer:

The displacement at any time t is s = \(\frac{t^2}{s}\)

∴ Velocity, v = \(\frac{ds}{dt}\) = \(\frac{2}{3}\)t*

∴ Work done = change in kinetic energy in time 2 s = \(\frac{1}{2} m v^2=\frac{1}{2} \times 3 \times\left(\frac{2}{3} \times 2\right)^2=2.67 \mathrm{~J}\)

The option 4 is correct.

Characteristics Of Wave Motion Class 11

Question 17. Which one of the kinematic equations states the work-energy principle?
Answer:

The equation \(\vec{F}=m \vec{a}\) states the work-energy principle.

Question 18. A particle moves from a point \(\vec{r}_1=\hat{i}+2 \hat{j}\) in meter to another point \(\overrightarrow{r_2}=2 \hat{i}+4 \hat{j}\)in meter under the action of a force \(\vec{F}=2 \hat{i}+3 \hat{j}\) in newton. Find the work done by the force on the particle in the displacement.
Answer:

Given, \(\vec{F}=2 \hat{i}+3 \hat{j}\); initial position, \(\overrightarrow{r_1}=(\hat{i}+2 \hat{j})\)m; final position, \(\overrightarrow{r_2}=(2 \hat{i}+4 \hat{j}) \mathrm{m}\).

Displacement, \(\vec{r}=\left(\vec{r}_2-\vec{r}_1\right)=[(2 \hat{i}+4 \hat{j})-(\hat{i}+2 \hat{j})]\)

= \((\hat{i}+2 \hat{j}) \mathrm{m}\)

∴ Work done, W = \(\vec{F} \cdot \vec{r}=(2 \hat{i}+3 \hat{j}) \cdot(\hat{i}+2 \hat{j})=8 \mathrm{~J}\)

Question 19. Work done for a certain spring when stretched through 1 mm is 10 J. The amount of work that must be done on the spring to stretch if further by 1 mm is

1. 30 J
2. 40 J
3. 10 J
4. 20 J

Answer:

Work done in stretching the spring, W = \(\frac{1}{2} k x^2\)

[the spring is stretched by x; force constant of the spring is k]

When x = 1 mm, work done W₁ = \(\frac{1}{2}\)k = 10 J

∴ k = 20 J

When the spring is stretched further 1 mm, x = 2 mm

∴ Work done, W₂ = \(\frac{1}{2}\)k(2)² = 2k = 40 J

So, work done to stretch the spring further by 40 -10 = 30 J

The option 1 is correct.

Question 20. A bullet of mass 4.2 x 10^-2 kg moving at a speed of 300 m/s, gets stuck into a block with a mass 9 times that of the bullet. If the block is free to move without any kind of friction, the heat generated in the process will be

1. 45 cal
2. 405 cal
3. 450 cal
4. 1701 cal

Answer:

Let, the mass of the bullet is m, the mass of the block is M, the speed of the bullet before the collision is v, and speed of the combined bullet and block system after the collision is v₁.

According to the law of conservation of momentum, \(m v=(m+M) \nu_1 \quad \text { or, } v_1=\frac{m}{m+M} \nu\)

Heat energy generated = loss of kinetic energy

= \(\frac{1}{2} m v^2-\frac{1}{2}(m+M) v_1^2\)

= \(\frac{1}{2} m v^2-\frac{1}{2}(m+M) \times \frac{m^2 v^2}{(m+M)^2}=\frac{1}{2} \frac{m M v^2}{(m+M)}\)

= \(\frac{1}{2} \times \frac{m \times 9 m \times 300^2}{(m+9 m)}=\frac{1}{2} \times \frac{9}{10} \times 4.2 \times 10^{-2} \times 300^2\)

= \(1701 \mathrm{~J}=\frac{1701}{4.2} \mathrm{cal}=405 \mathrm{cal}\)

The option 2 is correct.

Question 21. A small steel ball bounces on a steel plate held horizontally. On each bounce, the speed of the ball arriving at the plate is reduced by a factor e (coefficient of restitution) in the rebound so that \(V_{\text {upward }}=e V_{\text {downward }}\). If the ball is initially dropped from a height of 0.4 m above the plate and if 10 s later the bouncing ceases, the value of e is

1. \(\sqrt{\frac{2}{7}}\)
2. \(\frac{3}{4}\)
3. \(\frac{13}{18}\)
4. \(\frac{17}{18}\)

Answer:

We know, t = \(\sqrt{\frac{2 h}{g}}\left[\frac{1+e}{1-e}\right]\)

∴ 10 = \(\sqrt{\frac{2 \times 0.4}{10}}\left[\frac{1+e}{1-e}\right] \text { [taking } g=10 \mathrm{~m} / \mathrm{s}^2 \text { ] }\)

or, e = \(\frac{25 \sqrt{2}-1}{25 \sqrt{2}+1} \approx \frac{17}{18}\)

The option 4 is correct.

Question 22. A particle of mass m moving in the x direction with speed 2 v is hit by another particle of mass 2 m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to

1. 44%
2. 50%
3. 56%
4. 62%

Answer:

Due to the conservation of momentum along x-axis, \(m \cdot 2 v=(m+2 m) v_1 \quad \text { or, } v_1=\frac{2 v}{3}\)

Now, along y-axis, \(2 m \cdot v=(m+2 m) v_2 \quad \text { or, } v_2=\frac{2 v}{3}\)

So, velocity of the particle of mass (m+2 m=3 m) after collision, \(v^{\prime}=\sqrt{v_1^2+v_2^2}=\frac{2 \sqrt{2}}{3} v\)

Thus, energy loss = \(E_1-E_2\)

= \(\left\{\frac{1}{2} m(2 v)^2+\frac{1}{2}(2 m) v^2\right\}-\frac{1}{2} \cdot 3 m\left(\frac{2 \sqrt{2}}{3} \nu\right)^2\)

= \(3 m v^2-\frac{4}{3} m v^2=\frac{5}{3} m v^2\)

Hence, the percentage loss in energy

= \(\frac{E_1-E_2}{E_1} \times 100=\frac{\frac{5}{3} m v^2}{3 m v^2} \times 100=\frac{500}{9}=55.6 \approx 56\)

The option 3 is correct

Wave Motion Formula Class 11

Question 23. A point particle of mass m, moves along the uniformly rough track PQR as shown. The coefficient of friction between the particle and the rough track equals μ. The particle is released from rest from point P and it comes to rest at a point R. The energies lost by the ball, over the parts PQ and QR of the track are equal to each other and no energy is lost when the particle changes direction from PQ to QR. The values of the coefficient of friction μ and the distance x(=QR) are respectively close to

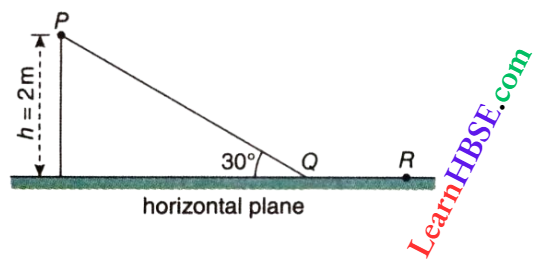
1. 0.2 and 6.5 m
2. 0.2 and 3.5 m
3. 0.29 and 3.5 m
4. 0.29 and 6.5 m

Answer:

As the energy lost over PQ and QR are equal, 2μmgcotθ = μmgx…(1)

∴ x = 2cotθ = 2cot30° ≈ 3.5 m

For work-energy theorem, mgh-2μmgcoθ – μmgx = 0

or, mgh-4μmgcotθ = 0 [using (1)]

∴ \(\mu=\frac{h}{4 \cot \theta}=\frac{2}{4 \cot 30^{\circ}}=\frac{1}{2 \sqrt{3}}=0.29\)

The option 3 is correct

Question 24. A person trying to lose weight by burning fat lifts a mass of 10 kg up to a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted? Fat supplies 3.8 x 10⁷ of energy- per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 m/s²

1. 2.45 x 10^-3 kg
2. 6.45 x 10^-3 kg
3. 9.89 x 10^-3 kg
4. 12.89 x 10^-3 kg

Answer:

Loss ofpotential energy = mgh x 1000 = 10 x 9.8 x 1 x 1000 = 9.8 x 10⁴ J

If fat of mass m is dissipated, then mechanical energy obtained

= \(m \times 3.8 \times 10^7 \times \frac{20}{100}=m \times 0.76 \times 10^7 \mathrm{~J}\)

According to the question, \(m \times 0.76 \times 10^7=9.8 \times 10^4\)

m = \(\frac{9.8 \times 10^4}{0.76 \times 10^7}=12.89 \times 10^{-3} \mathrm{~kg}\)

According to tire question, m x 0.76 x 10⁷ = 9.8 x 10⁴

∴ m = \(\frac{9.8 \times 10^4}{0.76 \times 10^7}=12.89 \times 10^{-3} \mathrm{~kg}\)

The option 4 is correct.

Question 25. A body of mass m = 10^-2 kg is moving in a medium and experiences a frictional force F = -kv². Its initial speed is v₀ = 10 m · s^-1. If after 10 s, its energy is \(\frac{1}{8}\)\(m v_0^2\), the value of k is

1. \(10^{-3} \mathrm{~kg} \cdot \mathrm{m}^{-1}\)
2. \(10^{-3} \mathrm{~kg} \cdot \mathrm{s}^{-1}\)
3. \(10^{-4} \mathrm{~kg} \cdot \mathrm{m}^{-1}\)
4. \(10^{-1} \mathrm{~kg} \cdot \mathrm{m}^{-1} \cdot \mathrm{s}^{-1}\)

Answer:

⇒ \(\frac{K_f}{K_i}=\frac{\frac{1}{8} m v_0^2}{\frac{1}{2} m v_0^2} \quad \text { or, } \frac{\frac{1}{2} m v_f^2}{\frac{1}{2} m v_0^2}=\frac{1}{4}\)

or, \(\frac{v_f}{v_0}=\frac{1}{2} \quad \text { or, } v_f=\frac{v_0}{2}=\frac{10}{2}=5 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Given, \(F=-k v^2\)

Also, \(\frac{d v}{d t}=\frac{F}{m}=\frac{-k v^2}{m}\)

∴ \(\int_{v_0=10}^{v_f=5} \frac{d v}{v^2}=-\frac{k}{m} \int_{t=0}^{t=10} d t\)

or, \(\left[-\frac{1}{v}\right]_{10}^5=-\frac{k}{m}[t]_0^{10}\) or, \(-\frac{1}{10}=-\frac{k}{m} \times 10\) or, \(k=10^{-4} \mathrm{~kg} \cdot \mathrm{m}^{-1}\)

The option 3 is correct

Wave Motion Class 11 Important Questions

Question 26. A time-dependent force F = 6t acts on a particle of mass 1 kg. If the particle starts from rest, the work done by the force during the first 1 s will be

1. 4.5 J
2. 22 J
3. 9J
4. 18 J

Answer:

Given, F = 6t

or, \(m \cdot \frac{d v}{d t}=6 t\)

or, \(\int_0^v d v=6 \int_0^1 t d t[m=1 \mathrm{~kg}]\)

or, \(v=6\left[\frac{t^2}{2}\right]_0^1=3 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

∴ Work done, W = \(\Delta \mathrm{KE}=\frac{1}{2} m v^2=\frac{1}{2} \times 1 \times 3^2=4.5 \mathrm{~J}\)

The option 1 is correct

Question 27. It is found that if a neutron suffers an elastic collinear collision with deuterium at rest, fractional loss of its energy is p_d; while for its similar collision with carbon nucleus at rest, fractional loss of energy is p_c. The values of p_d and p_c are respectively.

1. 0,0
2. 0,1
3. 0.89,0.28
4. 0.28,0.89

Answer:

In the first case, \(m u_n=m v_n+2 m \times v_D\)….(1)

(\(u_n\) and \(v_n\) are respectively initial and final velocity of neutron; \(v_D\) is the final velocity of deuterium)

∴ \(u_n=\left(v_D-v_n\right)\)[because e=1]…(2)

From (1) and (2) we get, \(v_n=-\frac{u_n}{3}\)

∴ \(p_d=\frac{\Delta E}{E}=\frac{\frac{1}{2} m u_n^2-\frac{1}{2} m v_n^2}{\frac{1}{2} m u_n^2}=\frac{8}{9}=0.89\)

In the second case, \(m u_n=m v_n^{\prime}+(12 m) \times v_C\)…(3)

(\(u_n\) and \(v_n^{\prime}\) are respectively initial and final velocity of neutron; \(v_C\) is the final velocity of carbon atom)

∴ \(u_n=v_c-v_n^{\prime}\)[because e=1]….(4)

From (3) and (4) we get, \(v_n^{\prime}=-\frac{11}{13} u_n\)

∴ \(p_c=\frac{\Delta E}{E}=\frac{\frac{1}{2} m u_n^2-\frac{1}{2} m\left(v_n^{\prime}\right)^2}{\frac{1}{2} m u_n^2}=\frac{48}{69}=0.28\)

Option 3 Correct

Question 28. A particle is moving in a circular path of radius a under the action of an attractive potential U = \(-\frac{k}{2 r^2}\). Its total energy is

1. Zero
2. \(-\frac{3}{2} \frac{k}{a^2}\)
3. \(-\frac{k}{4 a^2}\)
4. \(\frac{k}{2 a^2}\)

Answer:

F = \(-\frac{d U}{d r}=-\frac{k}{r^3}\)

This force provides the required centripetal force for circular motion of the particle.

∴ \(\frac{m v^2}{r}=\frac{k}{r^3}\)

or, \(m v^2=\frac{k}{r^2} \quad \text { or, } \frac{1}{2} m v^2=\frac{k}{2 r^2}\)

So, kinetic energy = \(\frac{k}{2 r^2}\)

The total energy of the particle = kinetic energy + potential energy

= \(\frac{k}{2 r^2}-\frac{k}{2 r^2}=0\)

The option 1 is correct

Wave Motion Derivation Class 11 Physics

Question 29. In a collinear collision, a particle with an initial speed v₀ strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is

1. \(\frac{v_0}{2}\)
2. \(\frac{v_0}{\sqrt{2}}\)
3. \(\frac{v_0}{4}\)
4. \(\sqrt{2} v_0\)

Answer:

From the law of conservation of linear momentum, mv₀ = mv₁ + mv₂

[m is the mass of the particles, v_1, and v₂ are the final velocities of the first and second particles respectively]

or, v₁ + v₂ = v₀ ….(1)

According to the question, \(\frac{1}{2} m\left(v_1^2+v_2^2\right)=\frac{3}{2}\left(\frac{1}{2} m v_0^2\right)\)

or, \(v_1^2+v_2^2=\frac{3}{2} v_0^2\)

or, \(\left(\nu_1+v_2\right)^2=\frac{3}{2} v_0^2+2 v_1 v_2\)

or, \(v_0^2-\frac{3}{2} v_0^2=2 v_1 v_2\) [from (1)]

or, \(2 v_1 v_2=-\frac{v_0^2}{2}\)

Now, \(\left(v_1-v_2\right)^2=v_1^2+v_2^2-2 v_1 v_2=\frac{3}{2} v_0^2+\frac{v_0^2}{2}=2 v_0^2\)

So, \(v_1-v_2=\sqrt{2} v_0\)

The option 4 is correct.

Question 30. A body of mass 4 m is lying in xy-plane at rest. It suddenly explodes into three pieces. Two pieces, each of mass m move perpendicular to each other with equal speeds v. The total kinetic energy generated due to the explosion is

1. mv²
2. \(\frac{3}{2}\)mv²
3. 2mv²
4. 4mv²

Answer:

By conservation of linear momentum, 2mv₁ = √2mv

or, \(v_1=\frac{v}{\sqrt{2}}\)

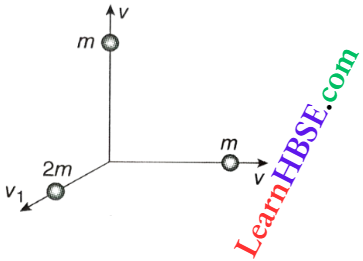
Total KE generated = \(\frac{1}{2} m v^2+\frac{1}{2} m v^2+\frac{1}{2}(2 m) v_1^2 v_1 \underset{O}{2 m}\)

= \(m v^2+m v_1^2=m v^2+\frac{1}{2} m \nu^2=\frac{3}{2} m v^2\)

The option 2 is correct.

Question 31. A particle of mass m is driven by a machine that delivers a constant power k watts. If the particle starts from rest the force on the particle at time t is

1. \(\sqrt{\frac{m k}{2}} t^{-1 / 2}\)
2. \(\sqrt{m k} t^{-1 / 2}\)
3. \(\sqrt{2 m k} t^{-1 / 2}\)
4. \(\frac{1}{2} \sqrt{m k} t^{-1 / 2}\)

Answer:

Work done =kt = \(\frac{1}{2}\)mv² = change in kinetic energy

∴ v = \(\sqrt{\frac{2 k t}{m}}\)

So, the required force = \(m a=m \frac{d v}{d t}=m \sqrt{\frac{2 k}{m}} \cdot \frac{1}{2} t^{-1 / 2}\)

= \(\sqrt{\frac{m k}{2}} t^{-1}\)

The option 1 is correct.

Types Of Wave Motion Class 11

Question 32. Two particles of masses m₁, m₂ move with initial velocities u₁ and u₂. On collision, one of the particles gets excited to a higher level, after absorbing energy ε. If the final velocities of particles are v₁ and v₂, then we must have

1. \(m_1^2 u_1+m_2^2 u_2-\varepsilon=m_1^2 v_1+m_2^2 v_2\)
2. \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2=\frac{1}{2} m_1 \nu_1^2+\frac{1}{2} m_2 \nu_2^2-\varepsilon\)
3. \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2-\varepsilon=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\)
4. \(\frac{1}{2} m_1^2 u_1^2+\frac{1}{2} m_2^2 u_2^2+\varepsilon=\frac{1}{2} m_1^2 \nu_1^2+\frac{1}{2} m_2^2 v_2^2\)

Answer:

A part of the initial kinetic energy ε excites a particle to a higher level. The remaining portion of the initial kinetic energy goes on to become the final kinetic energy.

The option 1 is correct.

Question 33. A body of mass 1 kg begins to move under the action of a time-dependent force \(\vec{F}=\left(2 t \hat{i}+3 t^2 \hat{j}\right) \mathrm{N}\), where \(\hat{i}\) and \(\hat{j}\) are unit vectors along x and y -axes. What power will be developed by the force at the time t?

1. (2t² + 4t⁴)W
2. (2t³ + 3t⁴)W
3. (2t³ + 3t⁵)W
4. (2t² + 3t³)W

Answer:

Acceleration of the particle at time t, \(\vec{a}=\frac{\vec{F}}{m}=\frac{2 t \hat{i}+3 t^2 \hat{j}}{1}=\left(2 t \hat{i}+3 t^2 \hat{j}\right) \mathrm{m} / \mathrm{s}^2\)

Velocity of the particle at time t, \(\vec{v}=\int_0^t \vec{a} d t=\int_0^t\left(2 t \hat{i}+3 t^2 \hat{j}\right) d t=\left(t^2 \hat{i}+t^3 \hat{j}\right) \mathrm{m} / \mathrm{s}\)

Power developed by the force at time r, \(P=\vec{F} \cdot \vec{v}=\left(2 \hat{t}+3 t^2 \hat{j}\right) \cdot\left(t^2 \hat{i}+t^3 \hat{j}\right)=\left(2 t^3+3 t^5\right) \mathrm{W}\)

The option 3 is correct.

Question 34. What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?

1. \(\sqrt{2 g R}\)
2. \(\sqrt{3 g R}\)
3. \(\sqrt{5 g R}\)
4. \(\sqrt{g R}\)

Answer:

The least velocity of a body of mass m at the lowest point on the vertical loop of radius R to complete the loop is given by u = \(\sqrt{5 g R}\)

The option 3 is correct

Question 35. A particle of mass 10 g moves along a circle of radius 6.4 cm with a constant tangential acceleration. What is the magnitude of this acceleration if the kinetic energy of the particle becomes equal to 8 x 10^-4 J by the end of the second revolution after the beginning of the motion?

1. \(0.15 \mathrm{~m} / \mathrm{s}^2\)
2. \(0.18 \mathrm{~m} / \mathrm{s}^2\)
3. \(0.2 \mathrm{~m} / \mathrm{s}^2\)
4. \(0.1 \mathrm{~m} / \mathrm{s}^2\)

Answer:

Kinetic energy of the particle, \(E=\frac{1}{2} m v^2=8 \times 10^{-4} \mathrm{~J}\)

or, \(\frac{1}{2} \times 10 \times 10^{-3} \times v^2=8 \times 10^{-4}\)

or,\(v^2=\frac{8 \times 10^{-4} \times 2}{10^{-2}}=0.16\)

∴ \(v=\sqrt{0.16}=0.4 \mathrm{~m} / \mathrm{s}\)

From \(v^2=u^2+2 a s\), \((0.4)^2=0+2 a \times 2(2 \pi r)=8 \pi r a\)

[s= distance covered by the particle =2(2πr); r= radius of the circle]

or, \(0.16=8 \times 3.14 \times 6.4 \times 10^{-2} \times a\)

or, \(a=\frac{0.16}{8 \times 3.14 \times 6.4 \times 10^{-2}}=0.1 \mathrm{~m} / \mathrm{s}^2\)

The option 4 is correct

Question 36. A body initially at rest, breaks up into two pieces of A masses 2 M and 3 M respectively, together having a total kinetic energy E. The piece of mass 2M, after breaking up, has a kinetic energy

1. \(\frac{2 E}{5}\)
2. \(\frac{E}{2}\)
3. \(\frac{E}{5}\)
4. \(\frac{3 E}{5}\)

Answer:

From the law of conservation of momentum, p₁ = p₂

Kinetic energy, E = \(\frac{p^2}{2 m} \quad \text { or, } E \propto \frac{1}{m}\)

∴ \(\frac{E_1}{E_2}=\frac{m_2}{m_1}=\frac{3 M}{2 M}=\frac{3}{2}\)

∴ \(\frac{E_1}{E_1+E_2}=\frac{3}{3+2}=\frac{3}{5}\)

or, \(\frac{E_1}{E}=\frac{3}{5} \quad \text { or, } E_1=\frac{3 E}{5}\)

The option 4 is correct

Question 37. A body starts moving unidirectionally under the influence of a source of constant power. Which one of the graphs correctly shows the variation of displacement (s) with time (t)?

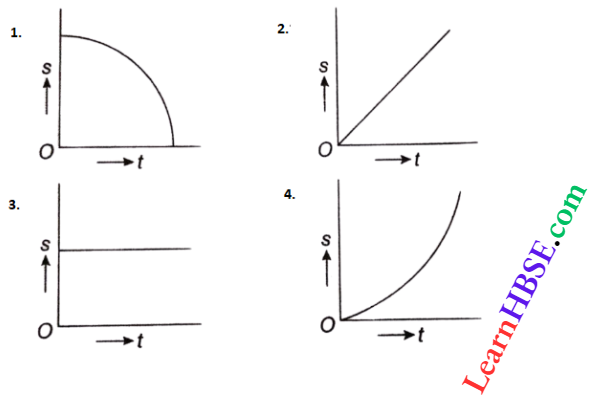
Answer:

We know, power

= work done per second

= increase in kinetic energy per second = constant

So, the velocity of the body increases with time

Therefore, slope (\(\frac{d s}{d t}\) = v) of the s-t graph increases
with time.

The option 4 is correct

Question 38. A body initially at rest and sliding along a frictionless track from a height h just completes a vertical circle of diameter AB = D. The height h is equal to

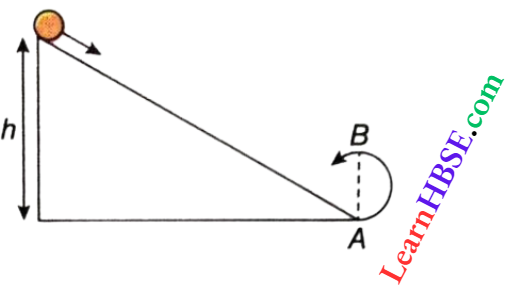
1. \(\frac{7}{5}\) D
2. D
3. \(\frac{3}{2}\) D
4. \(\frac{5}{4}\) D

Answer:

To complete a vertical circle of diameter D, the minimum speed at point A,

v = \(\sqrt{5 g R}=\sqrt{5 g \frac{D}{2}}\)

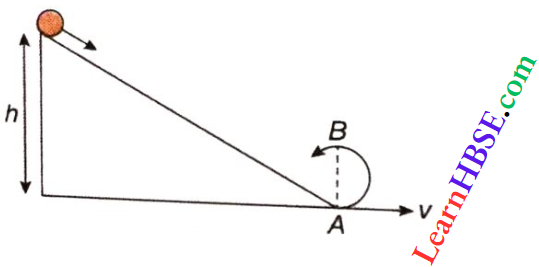
The potential energy of the body at height h, E_P = mgh

From the law of conservation of energy, 0 + mgh = \(\frac{1}{2} m v^2+0\)

or, \(m g h=\frac{1}{2} m \frac{5 g D}{2} or, h=\frac{5}{4} D\)

The option 4 is correct.

Question 39. A moving block having a mass m collides with another stationary block having a mass 4m. The lighter block comes to rest after collision. When the initial velocity of the lighter block is u, then the value of the coefficient of restitution (e) will be

1. 0.8
2. 0.25
3. 0.5
4. 0.4

Answer:

According to law of conservation of linear momentum, \(m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2\)

or, \(m \nu+0=0+4 m v_2\)

or, \(v_2=\frac{v}{4}\)

∴ Coefficient of restitution, e = \(\frac{\text { relative velocity of separation after collision }}{\text { relative velocity of approach before collision }}\)

∴ \(\frac{{v}{4}}{\nu}\) =0.25

The option 2 is correct

Question 40. Answer with reason: In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e., when they are in contact)?
Answer:

The collision produces a slight deformation of both balls. A part of the KE is used for that deformation; so the total KE is not conserved during the short time of collision. However, due to the elastic stress developed in the perfectly elastic balls, the kinetic energy is regained after the collision.

Question 41. The casting of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket the atmosphere, or both?
Answer:

Given

The casting of a rocket in flight burns up due to friction

The only source of energy is the kinetic energy of the rocket. The atmosphere does not contribute any energy. Its role is only to provide friction to convert the kinetic energy of the rocket into heat energy.

Question 42. If the force applied on an object is 5 N and the power expended by it is 20 W, what is the velocity of the object?
Answer:

Given

If the force applied on an object is 5 N and the power expended by it is 20 W

If the velocity v of the object and the force F acting on it are in the same direction, then the power expended is P = Fv.

Here, P = 20 W, F = 5 N.

∴ v = \(\frac{P}{F}=\frac{20}{5}=4 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Question 43. From the graph shown calculate the work done by the applied force and frictional force over a distance of 2 m.
Answer:

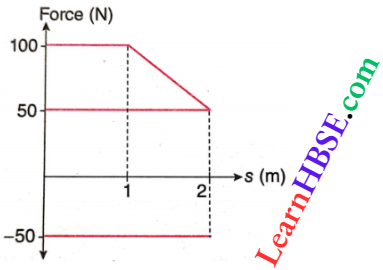
If the displacement s is along the direction of the force F, the work done is

W = ∫Fds = Area under the graph showing the variations on a force-displacement graph.

So, the work done by the applied force is, Wj = areas (A + B + C + D)

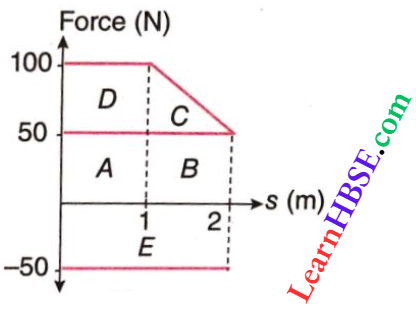
= 50 X 1 + 50 x (2- 1) + \(\frac{1}{2}\)(100- 50)(2- 1) + (100- 50) x 1

= 50 + 50 + 25 + 50 = 175 J

The work done by the frictional force is, W₂ = area of E = -50 x 2 = -100 J

Question 44. Two objects of masses in the ratio 1:2 collide elastically with each other. What is the ratio of their kinetic energies?
Answer:

Insufficient data

Question 45. Two bodies A and B weighing 5 kg and 6 kg respectively have equal momentums. Which one has more kinetic energy?
Answer:

Given

Two bodies A and B weighing 5 kg and 6 kg respectively have equal momentums.

Kinetic energy, \(E_k=\frac{1}{2} m v^2=\frac{1}{2} \frac{\left(m^2 v^2\right)}{m}=\frac{p^2}{2 m} .\)

where p = mv = momentum.

Thus the body with a lower mass of 5 kg, i.e., body A has higher kinetic energy.

Question 46. Two bodies of different masses have equal kinetic energies. Which will have more momentum?
Answer:

Given

Two bodies of different masses have equal kinetic energies.

Momentum, p = mv = \(\sqrt{m^2 v^2}=\sqrt{2 m \cdot \frac{1}{2} m v^2} \text {. }\)

= \(\sqrt{2 m E}\) (where E = kinetic energy]

For the two bodies, E is the same. So the momentum will be greater for the heavier body, as m is greater.

Question 47. Angad and Nalin were observing a building having two different staircases. One slanting and the other vertically spiral. Angad was of the opinion that a person using a slanting staircase will be doing more work against gravity but Nalin thought otherwise. They started quarreling. Arif, their friend, explained and gave an entirely different view and pacified them.

1. What according to you was the explanation given by Arif?
2. What appreciable values do you see in Arif?
3. Does it also follow with friction? Why or why not?

Answer:

1. Arif explained that gravitational force is a conservative force. Hence work done to lift a body to the same height will be the same, whatever may the nature of the path be. So, a person using a slanting staircase or a vertically spiral staircase will do the same work as the height is the same.
2. Arif is honest and he has the ability to explain the incident of nature scientifically.
3. In the case of a slanting staircase, the path traversed by a person is more than that of a vertically spiral staircase. For the longer path, the work done against friction will be more. So for friction, the total work done by a person using a slanting staircase will be more than that of a spiral staircase.

Question 48. The momentum of a body of mass 5 kg is 500 kg · m · s^-1. Find its kinetic energy.
Answer:

Given

The momentum of a body of mass 5 kg is 500 kg · m · s^-1.

Mass of the body, m = 5 kg; let the velocity of the body = v.

Momentum of the body = mv = 500 kg · m · s^-1

So, velocity of the body, v = \(\frac{m v}{m}\) = \(\frac{500}{5}\) = 100 m · s^-1.

Hence. Kinetic energy = \(\frac{1}{2} m v^2=\frac{1}{2} \times 5 \times(100)^2=25000 \mathrm{~J}=25 \mathrm{~kJ}\)

Question 49. State if the following statement is true or false. Give a reason for your answer. In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.
Answer:

The given statement is true.

Reason: In an inelastic collision, a part of the initial kinetic energy is converted to some other form of energy, for example, heat energy, or sound energy. This results in the reduction of kinetic energy. Hence, the final kinetic energy is always less than the initial kinetic energy.

Question 50. A ball of 0.1 kg makes an elastic collision with a ball of unknown mass that is initially at rest. If the 0.1 kg ball rebounds at one-third of its original speed, what is the mass of the other ball?
Answer:

Given

A ball of 0.1 kg makes an elastic collision with a ball of unknown mass that is initially at rest. If the 0.1 kg ball rebounds at one-third of its original speed,

For elastic collision, \(v_1=\frac{\left(m_1-m_2\right) u_1+2 m_1 u_2}{m_1+m_2}\)

(\(m_2\) = mass of the other ball, \(v_1\) = final velocity of the ball of mass 0.1 kg)

Now, \(m_1=0.1 \mathrm{~kg}, u_1=\nu ; u_2=0 ; v_1=-\frac{v}{3}\)

∴ \(-\frac{\nu}{3}=\frac{\left(0.1-m_2\right) \nu+0}{0.1+m_2}\)

or, \(-\nu \times 0.1-v m_2=0.3 \times \nu-3 \nu m_2\)

or, \(m_2=0.2 \mathrm{~kg}\)

Question 51. The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:

1. Work done by a man in lifting a bucket out of a well using a rope tied to the bucket.
2. Work done by friction on a body sliding down an inclined plane.
3. Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity.

Answer:

1. Work done is positive as both the force and displacement are in the same direction.
2. Work done is negative as the direction of friction is opposite to the direction of motion.
3. In order to maintain the uniform velocity, the applied force must act in the direction of motion of the body. Hence, the work done is positive.