Rotation Of Rigid Bodies Short Answer Type Questions
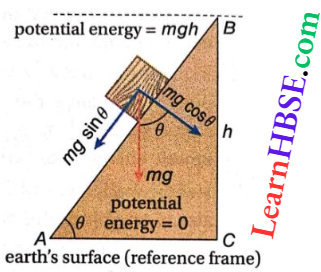
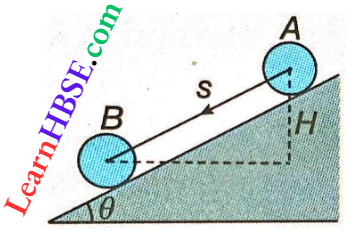
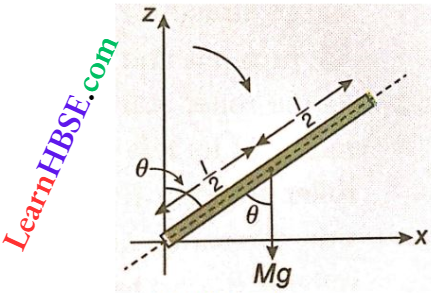
Question 1. A disc of mass M and radius R is rolling without slipping down an inclined plane. Show that the acceleration of the centre of mass of the disc c is \(\frac{2}{3}\)gsinθ. Given that, angle of inclination of the plane is θ and the moment of inertia of the disc is \(\frac{M R^2}{2}\).
Answer:
Given
A disc of mass M and radius R is rolling without slipping down an inclined plane.
Given that, angle of inclination of the plane is θ and the moment of inertia of the disc is \(\frac{M R^2}{2}\)
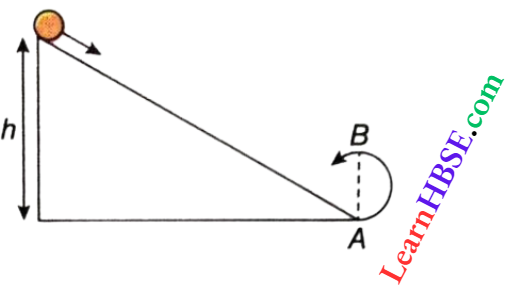
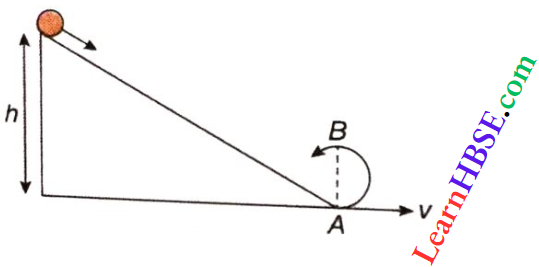
Let at A the velocity of the disc = 0, i.e., kinetic energy = 0.
Now the disc sliding along the inclined plane reaches at point B. Suppose, the velocity of the disc be v, so the angular velocity is ω = \(\frac{v}{R}\).
Hence kinetic energy,
\(K =\frac{1}{2} M \nu^2+\frac{1}{2} I \omega^2=\frac{1}{2} M v^2+\frac{1}{2} \cdot \frac{1}{2} M R^2 \frac{v^2}{R^2}\)
= \(\frac{3}{4} M v^2\)
So, an increase in kinetic energy from A to B = \(\frac{3}{4} M v^2-0=\frac{3}{4} M v^2\)
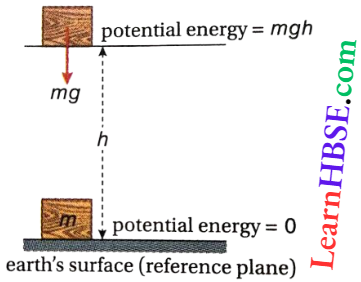
Decrease in potential energy from A to B = \(M g H=M g s \sin \theta\)
∴ \(\frac{3}{4} M v^2=M g s \sin \theta \quad \text { or, } v^2=\frac{4}{3} g s \sin \theta\)
When acceleration of the centre of mass of the disc is a, v² = 2as.
∴ \(2 a s=\frac{4}{3} g s \sin \theta\)
or, \(a=\frac{2}{3} g \sin \theta\)
Question 2. Show that the angular momentum of a particle under the action of the force \(\vec{F}=k \vec{r}\) is conserved, where k is a constant quantity.
Answer:
Torque, \(\vec{\tau}=\vec{r} \times \vec{F}=\vec{r} \times \overrightarrow{k r}=0\)
So, \(\vec{\tau}=\frac{d \vec{L}}{d t}=0\)
i.e., angular momentum (\(\vec{L}\)) is conserved.
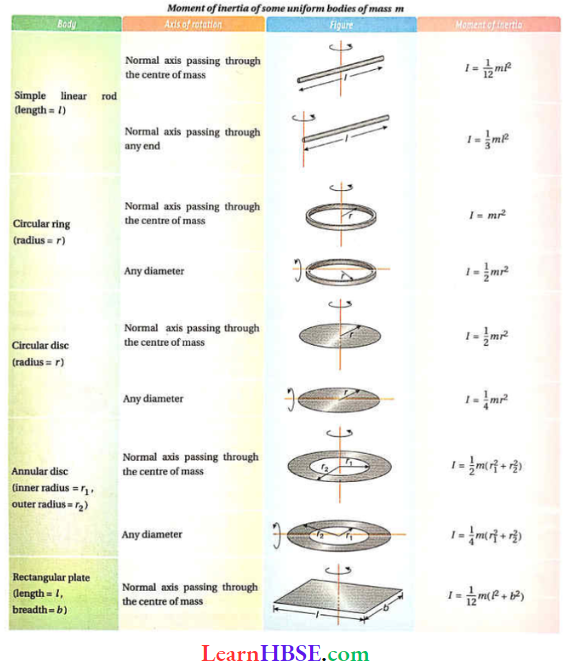
Question 3. If the moment of inertia of a solid sphere of mass M and radius R is \(\frac{2}{5}\)MR², what will be the radius of gyration?
Answer:
Given
The moment of inertia of a solid sphere of mass M and radius R is \(\frac{2}{5}\)MR²
If k is the radius of gyration, then moment of inertia = Mk²
Here, \(M k^2=\frac{2}{5} M R^2 \quad \text { or, } k=R \sqrt{\frac{2}{5}}\)
Question 3. Four point masses, each of mass m, are arranged in the xy-plane at the points (0,0), (a, a), (a, -a) and (2a, 0) respectively. What is the moment of inertia of this array of masses about the y-axis?
Answer:
Given
Four point masses, each of mass m, are arranged in the xy-plane at the points (0,0), (a, a), (a, -a) and (2a, 0) respectively.
The moment of inertia of the array of four-point masses about the y-axis, \(I_y=m_1 x_1^2+m_2 x_2^2+m_3 x_3^2+m_4 x_4^2\)
= \(m \times 0+m \times a^2+m \times a^2+m \times(2 a)^2\)
= \(6 m a^2\)
Question 4. The moment of inertia of a uniform circular disc of mass M and radius R about its diameter is \(\frac{1}{4}\)MR². What is the moment of inertia of the disc about an axis passing through its centre and perpendicular to the plane of the disc?
Answer:
Given
The moment of inertia of a uniform circular disc of mass M and radius R about its diameter is \(\frac{1}{4}\)MR².
If we consider another diameter on the plane of the disc perpendicular to the diameter mentioned in the question, the moment of inertia of the disc will also be \(\frac{1}{4}\)MR².
The intersection point of these two diameters is the centre of the disc; so the moment of inertia of the disc about an axis passing through its centre and perpendicular to the plane of the disc (according to the perpendicular axis theorem),
I = \(\frac{1}{4} M R^2+\frac{1}{4} M R^2=\frac{1}{2} M R^2\)
Question 5. A uniform solid sphere of mass M and radius R rolls down an inclined plane making an angle θ with the horizontal without slipping. Show that the acceleration of the sphere is \(\frac{5}{7}\)gsinθ. [Given: moment of inertia of the sphere is \(\frac{2}{5}\)MR²]
Answer:
Given
A uniform solid sphere of mass M and radius R rolls down an inclined plane making an angle θ with the horizontal without slipping.
moment of inertia of the sphere is \(\frac{2}{5}\)MR²
The forces acting on the sphere are frictional force (f), normal force (n) and weight (Mg). The net force on the sphere acting parallel to the inclined plane = Mgsinθ-f
If the linear acceleration of the sphere is a, Mgsinθ – f = Ma…(1)
The moment of inertia of the sphere, I = \(\frac{2}{5}\)MR²
If the angular acceleration of the sphere about its centre is α, the torque on the sphere, τ = Iα = fR
∴ f = \(\frac{I a}{R}=\frac{I a}{R^2}\) (because \(a=\frac{a}{R}\))….(2)
From equation (1) we get, \(M g \sin \theta-\frac{I a}{R^2}=M a\)
or, \(a=\frac{g \sin \theta}{1+\frac{I}{M R^2}}=\frac{g \sin \theta}{1+\frac{2}{5}}=\frac{5}{7} g \sin \theta\)
Question 6. A uniform solid spherical ball is rolling down a smooth inclined plane from a height h. The velocity attained by the ball when it reaches the bottom of the inclined plane is v. If the ball is now thrown vertically upwards with the same velocity v, the maximum height to which the ball will rise is
- \(\frac{5 h}{8}\)
- \(\frac{3 h}{5}\)
- \(\frac{5 h}{7}\)
- \(\frac{7 h}{9}\)
Answer:
I = \(\frac{2}{5}\)mr², where r = radius of the ball, m = mass of the ball
so, mgh = \(\frac{1}{2} m v^2+\frac{1}{2} I \omega^2 \quad \text { or, } v=\sqrt{\frac{10 g h}{7}}\)
In the case of the upward motion of the ball, \(v^2=u^2-2 g h^{\prime} \quad \text { or, } u^2=2 g h^{\prime}\) [v=0]
or, \(\frac{10 g h}{7}=2 g h^{\prime} \quad or, h^{\prime}=\frac{5 h}{7}\)
The option 3 is correct
Question 7. A solid uniform sphere resting on a rough horizontal plane is given a horizontal impulse directed through its centre so that it starts sliding with an initial velocity v0. When it finally starts rolling without slipping the speed of its centre is
- \(\frac{2}{7}\)v0
- \(\frac{3}{7}\)v0
- \(\frac{5}{7}\)v0
- \(\frac{6}{7}\)v0
Answer:
The angular momentum remains conserved along the point of contact between the sphere and the inclined plane.
So, \(m v_0 R=m v R+\frac{2}{5} m R^2\left(\frac{\nu}{R}\right) \quad \text { or, } v=\frac{5}{7} v_0\)
The option 3 is correct
Question 8. A thin rod AB has held horizontally so that it can freely rotate in a vertical plane about the end A as shown. The potential energy of the rod when it hangs vertically is taken to be zero. The end B of the rod is released from rest from a horizontal position. At the instant, the rod makes an angle θ with the horizontal,
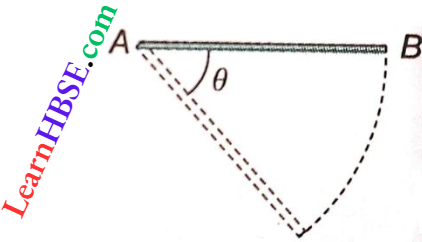
- The speed of end B is proportional to \(\sqrt{\sin \theta}\)
- The potential energy is proportional to (1- cosθ)
- The angular acceleration is proportional to cosθ
- The torque about A remains the same as its initial value
Answer:
Decrease in potential energy of the centre of mass of the rod = increase in kinetic energy of the centre of mass of the rod
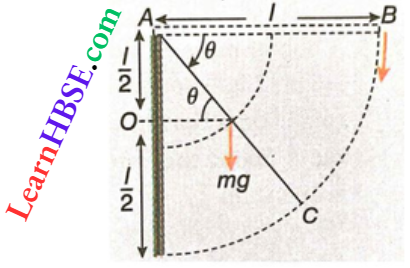
or, \(m g \times A O=\frac{1}{2} I \omega^2\)
[I = moment of inertia of the rod]
or, \(m g \times \frac{l}{2} \sin \theta=\frac{1}{2} I \omega^2\)
or, \(\omega \propto \sqrt{\sin \theta}\)
or, \(\nu \propto \sqrt{\sin \theta}\)
Torque, \(\tau=I \omega\)
or, \(m g \times \frac{l}{2} \cos \theta=\frac{m l^2}{3} \alpha \quad or, \alpha \propto \cos \theta\)
Option 1 and 3 is correct
Question 9. Three identical square plates rotate about the axes shown in such a way that their kinetic energies are equal. Each of the rotation axes passes through the centre of the square. Then the ratio of angular speeds ω1 : ω2: ω3 is
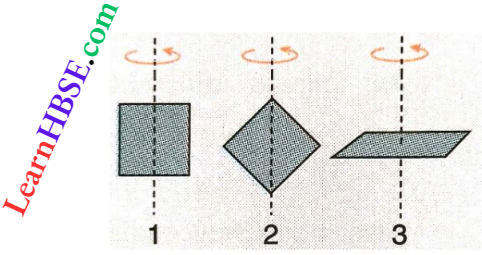
- 1:1:1
- √2:√2:1
- 1:√2:1
- 1:2:√2
Answer:
Kinetic energy, K = \(\frac{1}{2}\)Iω²
According to the question, K = constant
∴ \(\omega \propto \frac{1}{\sqrt{I}}\)
⇒ \(I_1=I_2=\frac{1}{12} R^2 m\)
[l = length of the side of square and m = mass of the square plate]
and \(I_3=\frac{1}{6} R^2 m\)
∴ \(\omega_1: \omega_2: \omega_3=\frac{1}{\sqrt{I_1}}: \frac{1}{\sqrt{I_2}}: \frac{1}{\sqrt{I_3}}\)
= \(\sqrt{12}: \sqrt{12}: \sqrt{6}=\sqrt{2}: \sqrt{2}: 1\)
The option 2 is correct.
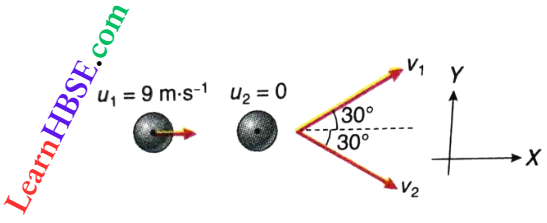
Question 10. Two particles A and B are moving as shown. Their total angular momentum g about the point O is
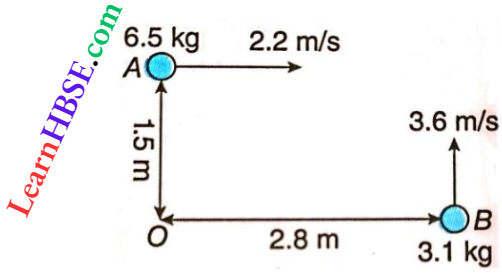
- 9.8 kg m²s
- Zero
- 52.7 kg m²/s
- 37.9 kg m²/s
Answer:
Momentum (\(\vec{p}=m\vec{v}\)) and distance (\(\vec{r}\)) from the axis of rotation these two vectors are perpendicular to each other for both A and B.
So, angular momentum, L = mvr
According to the given figure, L = L1 + L2 = 6.5 x 2.2 x 1.5- 3.1 x 3.6 x 2.8 = -9.8 kg · m²/s
So the value of the angular momentum = 9.8 kg · m²/s
The option 1 is correct.
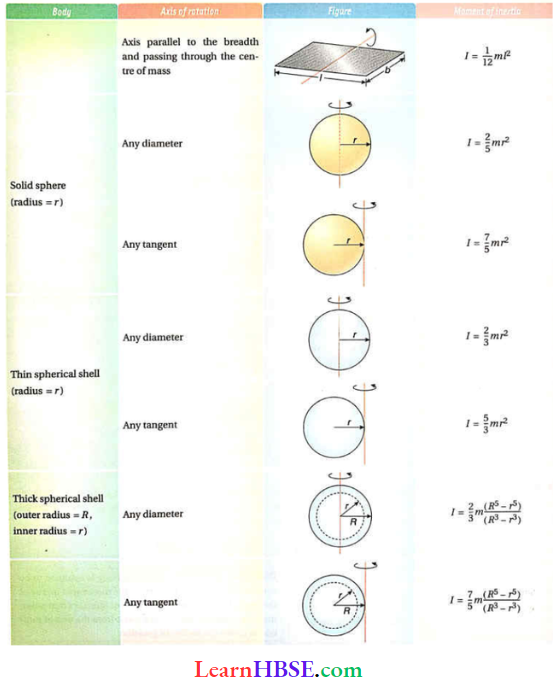
Question 11. A solid spherical ball and a hollow spherical ball of two different materials of densities ρ1 and ρ2 respectively have the same outer radii and the same mass. What will be the ratio of the moment of inertia (about an axis passing through the centre) of the hollow sphere to that of the solid sphere?
- \(\frac{\rho_2}{\rho_1}\left(1-\frac{\rho_2}{\rho_1}\right)^{5 / 3}\)
- \(\frac{\rho_2}{\rho_1}\left[1-\left(1-\frac{\rho_2}{\rho_1}\right)^{5 / 3}\right]\)
- \(\frac{\rho_2}{\rho_1}\left(1-\frac{\rho_1}{\rho_2}\right)^{5 / 3}\)
- \(\frac{\rho_2}{\rho_1}\left[1-\left(1-\frac{\rho_1}{\rho_2}\right)^{5 / 3}\right]\)
Answer:
⇒ \(\frac{4}{3} \pi R^3 \rho_2-\frac{4}{3} \pi R_1^3 \rho_2=\frac{4}{3} \pi R^3 \rho_1\)
or, \(R^3 \rho_2-R^3 \rho_1=R_1^3 \rho_2\)
or, \(R_1=R\left(1-\frac{\rho_1}{\rho_2}\right)^{1 / 3}\)
∴ \( \frac{I_{\text {hollow }}}{I_{\text {solid }}}=\frac{\frac{4}{3} \pi R^3 \rho_2 \times \frac{2}{5} R^2-\frac{4}{3} \pi R_1^3 \rho_2 \times \frac{2}{5} R_1^2}{\frac{4}{3} \pi R^3 \rho_1 \times \frac{2}{5} R^2}\)
= \(\frac{\rho_2\left(R^5-R_1^5\right)}{\rho_1 R^5}=\frac{\rho_2}{\rho_1}\left(1-\frac{R_1^5}{R^5}\right)\)
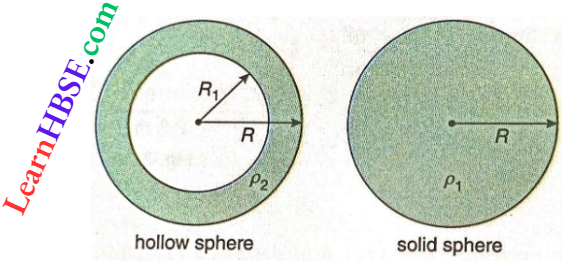
= \(\frac{\rho_2}{\rho_1}\left\{1-\left(1-\frac{\rho_1}{\rho_2}\right)^{5 / 3}\right\}\)
The option 4 is correct.
Question 12. A mass m supported by a massless string would be around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall on release?
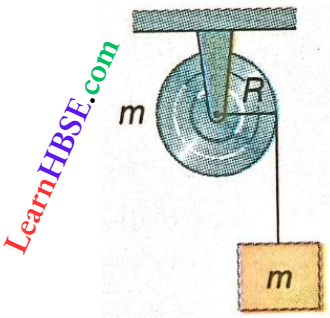
- \(\frac{2g}{3}\)
- \(\frac{g}{2}\)
- \(\frac{5g}{6}\)
- g
Answer:
Let a = downward acceleration of mass m
Its apparent weight = m(g- a)
Torque on the hollow cylinder = m(g- a)R
Now, angular acceleration, \(\alpha=\frac{\text { torque }}{\text { moment of inertia }}=\frac{m(g-a) R}{m R^2}=\frac{(g-a)}{R}\)
So, linear acceleration a = αR = g -a or, 2a = g or, a = \(\frac{g}{2}\)
The option 2 is correct.
Question 13. A block of mass m is placed on a surface with a vertical cross-section given by y = \(\frac{x^3}{6}\). If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is
- \(\frac{1}{6}\) m
- \(\frac{2}{3}\) m
- \(\frac{1}{3}\) m
- \(\frac{1}{2}\) m
Answer:
Angle of repose, θ = tan-1μ or, tanθ = 0.5
The surface y = \(\frac{x^3}{6}\) is curved.
At any point on it, \(\tan \theta=\frac{d y}{d x}=\frac{3 x^2}{6}=\frac{x^2}{2} \quad \text { or, } \frac{x^2}{2}=0.5\)
∴ x = 1
So, maximum height, \(y_m=\frac{1^3}{6}=\frac{1}{6} \mathrm{~m}\)
The option 1 is correct.
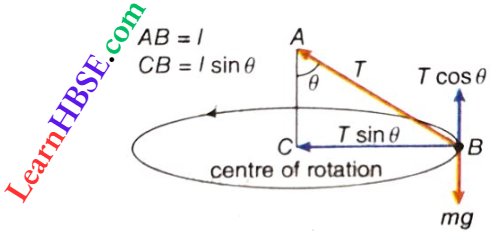
Question 14. A bob of mass m attached to an inextensible string of length l is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω rad/s about the vertical support. About the point of suspension
- Angular momentum is conserved
- Angular momentum changes in magnitude but not in direction
- Angular momentum changes in direction but not in magnitude
- Angular momentum changes both in direction and magnitude
Answer:
Magnitude of radius vector \(\vec{r}=|\vec{r}|=l\) = constant.
Magnitude of the momentum \(\vec{p}\) of the bob
= \(|\vec{p}|\) = M = mv = constant
As angular momentum \(\vec{L}=\vec{r} \times \vec{p}\) and the angle between \(\vec{r}\) and \(\vec{p}\) is always 90°,
⇒ \(|\vec{L}|=l \cdot m \omega l \cdot \sin 90^{\circ}=m l^2 \omega=\text { constant }\)
Also, \(\vec{r}\) is always radially outwards and \(\vec{p}\) is tangential.
So \(\vec{L}\) is always directed along the axis of rotation. So its direction is also fixed.
The option 1 is correct
Question 15. From a solid sphere of mass M and radius R a cube of maximum possible volume is cut. The moment of inertia of a cube about an axis passing through its centre and perpendicular to one of its faces is
- \(\frac{M R^2}{32 \sqrt{2} \pi}\)
- \(\frac{M R^2}{16 \sqrt{2} \pi}\)
- \(\frac{4 M R^2}{9 \sqrt{3} \pi}\)
- \(\frac{4 M R^2}{3 \sqrt{3} \pi}\)
Answer:
Let a be the side of the cube.
So, its diagonal = \(2 R=\sqrt{a^2+a^2+a^2}=\sqrt{3} a\)
or, \(a=\frac{2}{\sqrt{3}} R\)
Hence, volume of the cube = \(a^3=\frac{8}{3 \sqrt{3}} R^3\)
Now, density of the material of the sphere = \(\frac{M}{\frac{4}{3} \pi R^3}=\frac{3 M}{4 \pi R^3}\)
So the mass of the cube = \(\frac{3 M}{4 \pi R^3} \cdot \frac{8}{3 \sqrt{3}} R^3=\frac{2 M}{\sqrt{3} \pi}\)
Now let \(\frac{2 M}{\sqrt{3} \pi}=M^{\prime}\)
Hence, required moment of inertia
= \(\frac{1}{12} M^{\prime}\left(a^2+a^2\right)=\frac{1}{6} \cdot \frac{2 M}{\sqrt{3} \pi} \cdot\left(\frac{2}{\sqrt{3}} R\right)^2=\frac{4 M R^2}{9 \sqrt{3} \pi}\)
The option 3 is correct.
Question 16. A particle of mass m is moving along the side of a square of side a1 with a uniform speed v in the xy-plane as shown. Which of the following statements is false for the angular momentum \(\vec{L}\) about the origin?
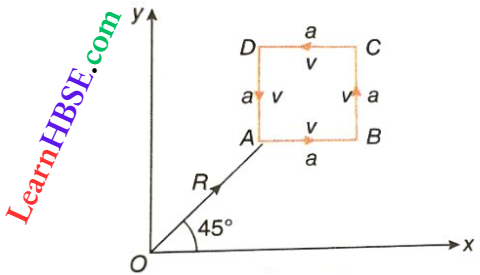
- \(\vec{L}=-\frac{m \nu R}{\sqrt{2}} \hat{k}\) when the particle is moving from A to B
- \(\vec{L}=m \nu\left[\frac{R}{\sqrt{2}}-a\right] \hat{k}\) when the particle is moving from C to D
- \(\vec{L}=m \nu\left[\frac{R}{\sqrt{2}}+a\right] \hat{k}\) when the particle is moving from B to C
- \(\vec{L}=\frac{m v}{\sqrt{2}} R \hat{k}\)nwhen the particle is moving from D to A
Answer: When the particle is moving from A to B, the angular momentum
⇒ \(\vec{L}=\vec{R} \times m \vec{v}=\left(\frac{R}{\sqrt{2}} \hat{i}+\frac{R}{\sqrt{2}} \hat{j}\right) \times m v \hat{i}=-\frac{R}{\sqrt{2}} m v \hat{k}\)
When the particle is moving from B to C, \(\vec{L}=(\vec{R}+\vec{a}) \times m \vec{v}=\left(\frac{R}{\sqrt{2}} \hat{i}+\frac{R}{\sqrt{2}} \hat{j}+a \hat{i}\right) \times m v \hat{j}\)
= \(\left(\frac{R}{\sqrt{2}}+a\right) m v \hat{k}\)
When the particle is moving from C to D, \(\vec{L}=\left(\frac{R}{\sqrt{2}} \hat{i}+\frac{R}{\sqrt{2}} \hat{j}+a \hat{i}+a \hat{j}\right) \times m v(-\hat{i})=\left(\frac{R}{\sqrt{2}}+a\right) m v \hat{k}\)
When the particle is moving from D to A, \(\vec{L}=(\vec{R}-\vec{a}) \times m \vec{v}\)
= \(\left[\frac{R}{\sqrt{2}} \hat{i}+\frac{R}{\sqrt{2}} \hat{j}-a(-\hat{j})\right] \times m v(-\hat{j})=-\frac{R}{\sqrt{2}} m v \hat{k}\)
The option 2 and 4 is false.
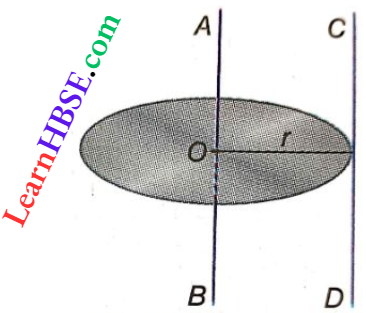
Question 16. A roller is made by joining together two cones at their vertices O. It is kept on two rails AB and CD which are placed asymmetrically, with its axis perpendicular to CD and its centre O at the centre of the line joining AB and CD. It is given a light push so that it starts rolling with its centre O moving parallel to CD in the direction shown. As it moves, the roller will tend to

- Turn left
- Turn right
- Go straight
- Turn left and right alternately
Answer:
As the roller starts to roll to the forward direction, the radius of its left part decreases. So, the left side of the roller traverses less distance along AB than the right side for the same number of rotations. That is why the roller will tend to turn left.
The option 1 is correct.
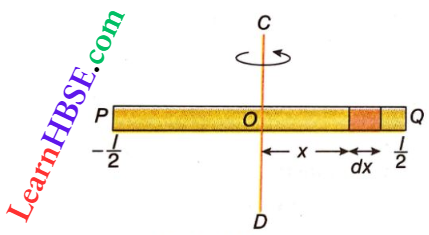
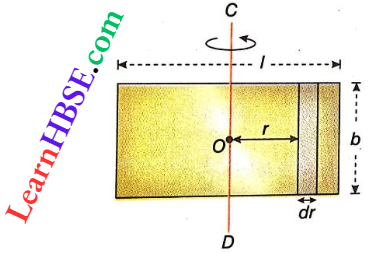
Question 17. The moment of inertia of a uniform cylinder of length l and radius R about its perpendicular bisector is I. What is the ratio \(\frac{1}{R}\) such that the moment of inertia is minimum?
- \(\sqrt{\frac{3}{2}}\)
- \(\frac{\sqrt{3}}{2}\)
- 1
- \(\frac{3}{\sqrt{2}}\)
Answer:
I = \(\frac{M R^2}{12}+\frac{M R^2}{4}\)
But M=\(\pi R^2 l \rho\)
(\(\rho\)= density of the material of the cylinder) or, \(R^2=\frac{M}{\pi \rho l}\)
∴ I = \(\frac{M l^2}{12}+\frac{M^2}{4 \pi \rho l} \quad \text { or, } \frac{d I}{d l}=\frac{2 M l}{12}-\frac{M^2}{4 \pi \rho}\left(\frac{1}{l^2}\right)\)
For the minimum value of I, \(\frac{d I}{d l}=0\)
Hence, \(\frac{2 M l}{12}-\frac{M^2}{4 \pi \rho}\left(\frac{1}{l^2}\right)=0\) or, \(\frac{l}{R}=\sqrt{\frac{3}{2}}\)
The option 4 is correct
Question 18. A slender uniform rod of mass M and length l is pivoted at one end so that it can rotate in a vertical plane. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod, when it makes an angle θ with the vertical, is:
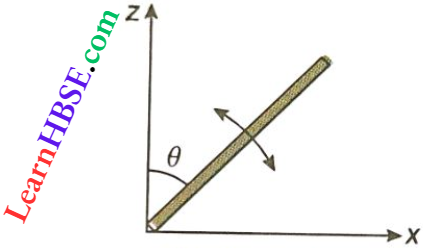
- \(\frac{3 g}{2 l} \sin \theta\)
- \(\frac{2 g}{3 l} \sin \theta\)
- \(\frac{3 g}{2 l} \cos \theta\)
- \(\frac{2 g}{3 l} \cos \theta\)
Answer:
When the rod is inclined at an angle θ then the torque on it, \(\tau=M g \sin \theta \cdot \frac{l}{2}\)
or, \(I \alpha=M g \sin \theta \cdot \frac{l}{2}\)
or, \(\frac{M l^2}{3} \cdot \alpha=M g \sin \theta \cdot \frac{l}{2}\)
or, \(\alpha=\frac{3 g \sin \theta}{2 l}\)
The option 1 is correct.
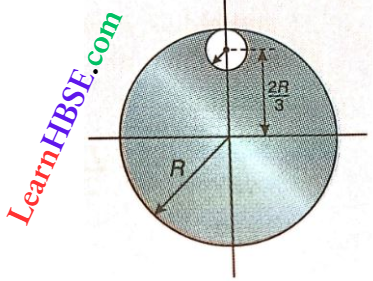
Question 19. From a uniform circular disc of radius R and mass 9M, a small disc of radius \(\frac{R}{3}\) is removed as shown. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through the centre of the disc is
- 10MR²
- \(\frac{37}{9}\)MR²
- 4MR²
- \(\frac{40}{9}\)MR²
Answer:
The mass of the circular disc of radius R = 9M
Therefore, the mass of the removed small disc of radius \(\frac{R}{3}\)
= \(9 M \times \frac{\pi\left(\frac{R}{3}\right)^2}{\pi R^2}=M\)
The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of the disc
= \((9 M) \frac{R^2}{2}-\left[\frac{M\left(\frac{R}{3}\right)^2}{2}+M\left(\frac{2 R}{3}\right)^2\right]=\frac{9}{2} M R^2-\frac{M R^2}{2}\)
The option 3 is correct.
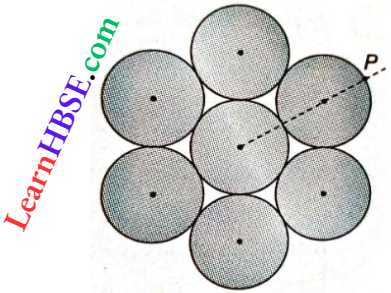
Question 20. Seven identical circular planar discs, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of r the arrangement about the V axis normal to the plane x and passing through the P is
- \(\frac{73}{2} M R^2\)
- \(\frac{181}{2} M R^2\)
- \(\frac{19}{2} M R^2\)
- \(\frac{55}{2} M R^2\)
Answer:
⇒ \(I_O=\frac{M R^2}{2}+6\left[\frac{M R^2}{2}+M(2 R)^2\right]\)
[the point O is the centre of mass of the arrangement]
=\(M R^2\left(\frac{1}{2}+3+24\right)\) = \(\frac{55}{2} M R^2\)
The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is \(I_P=I_O+7 M(3 R)^2=\frac{55}{2} M R^2+63 M R^2=\frac{181}{2} M R^2\)
The option 2 is correct
Question 21. The ratio of the accelerations for a solid sphere (mass m and radius R) rolling down an incline of angle Q without slipping and slipping down the incline without rolling is
- 5:7
- 2:3
- 2:5
- 7:5
Answer:
⇒ \(a_{\text {slipping }}=g \sin \theta, a_{\text {rolling }}=\frac{g \sin \theta}{1+\frac{k^2}{r^2}}\)
For sphere, \(k=\sqrt{\frac{2}{5}} r\)
∴ \(k^2=\frac{2}{5} r^2\)
So, \(a_{\text {rolling }}=\frac{g \sin \theta}{1+\frac{2}{5}}=\frac{5}{7} g \sin \theta\)
∴ \(\frac{a_{\text {rolling }}}{a_{\text {slipping }}}=\frac{\frac{5}{7} g \sin \theta}{g \sin \theta}=\frac{5}{7}\)
Option 1 is correct
Question 22. A mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0. The mass is attached to a string which passes through a smooth hole in the plane as shown.
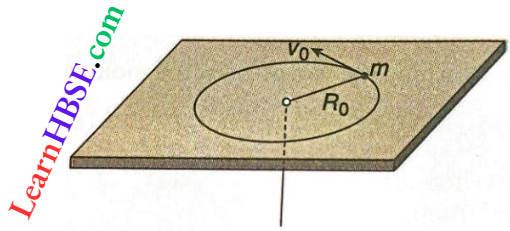
The tension in the string is increased gradually and finally, m moves in a circle of radius \(\frac{R_0}{2}\). The final value of the kinetic energy is
- \(m v_0^2\)
- \(\frac{1}{4} m v_0^2\)
- \(2 m v_0^2\)
- \(\frac{1}{2} m v_0^2\)
Answer:
The torque acting on the moving mass is directed upward.
The increasing tension in the string does not have any effect on the torque.
As a result, angular momentum will remain conserved,
i.e., \(m v_0 R_0=m v \frac{R_0}{2} \quad \text { or, } v=2 v_0\)
Hence, kinetic energy = \(\frac{1}{2} m\left(2 v_0\right)^2=2 m v_0^2\)
The option 3 is correct.
Question 23. Three identical spherical shells, each of mass m and radius r are placed as shown. Consider an axis xx’ which is touching to two shells and passing through the diameter of the third shell. Moment of inertia of the system consisting of these three spherical shells about xx’ axis is
- \(\frac{11}{5} m r^2\)
- \(3 m r^2\)
- \(\frac{16}{5} m r^2\)
- \(4 m r^2\)
Answer:
The moment of inertia of any spherical shell with respect to its diameter = \(\frac{2}{3}\)mr²
and moment of inertia with respect to tangent = \(\frac{2}{3} m r^2+m r^2=\frac{5}{3} m r^2\)
Hence, moment of inertia of the whole system = \(\frac{2}{3} m r^2+2 \times \frac{5}{3} m r^2=4 m r^2\)
The option 4 is correct
Question 24. From a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
- \(\frac{13 M R^2}{32}\)
- \(\frac{11 M R^2}{32}\)
- \(\frac{9 M R^2}{32}\)
- \(\frac{15 M R^2}{32}\)
Answer:
The mass of the removed part, \(M^{\prime}=\frac{M}{\pi R^2} \times \pi\left(\frac{R}{2}\right)^2=\frac{M}{4}\)
The moment of inertia of the disc about the perpendicular axis passing through the centre, I = \(\frac{MR^2}{2}\)
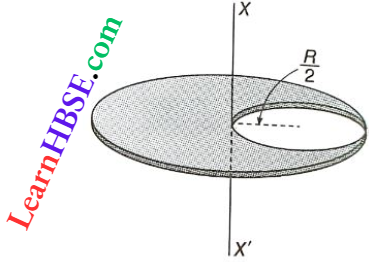
The moment of inertia of the removed part about XX’,
⇒ \(I^{\prime}=I_{\mathrm{cm}}+M^{\prime} d^2\)
= \(\frac{\frac{M}{4}\left(\frac{R}{2}\right)^2}{2}+\frac{M}{4}\left(\frac{R}{2}\right)^2\)
= \(\frac{M R^2}{32}+\frac{M R^2}{16}=\frac{3 M R^2}{32}\)
∴ The moment of inertia of the remaining part of the disc about XX’,
⇒ \(I^{\prime \prime}=I-I^{\prime}=\frac{M R^2}{2}-\frac{3 M R^2}{32}=\frac{13 M R^2}{32}\)
The option 1 is correct
Question 25. A disc and a sphere of same radius but different masses roll off on two inclined planes of the same altitude and length. Which one of the two objects gets to the bottom of the plane first?
- Sphere
- Both reach at the same time
- Depends on their masses
- Disc
Answer:
In the case of rolling down on the plane, the time taken by an object to reach to the bottom of the plane,
t = \(\frac{1}{\sin \theta} \sqrt{\frac{2 h}{g}\left(1+\frac{k^2}{R^2}\right)}\)
[where, h = the vertical height from which the object starts to roll down, θ = angle of inclination of the plane]
In the case of the disc, \(\frac{k^2}{R^2}=\frac{1}{2}=0 \cdot 5\)
In the case of the sphere, \(\frac{k^2}{R^2}=\frac{2}{5}=0.4\)
The time taken by the sphere is less than the disc to reach the bottom of the plane.
Hence, the sphere gets to the bottom of the plane first.
The option 1 is correct.
Question 26. The angular momentum of a rigid body of mass m about an axis is n times the linear momentum (P) of the body. The total kinetic energy of the rigid body is
- \(\frac{n^2 p^2}{2}\)
- \(\frac{P^2\left[1+n^2\right]}{2 m}\)
- \(\frac{n^2 P^2}{2 m}\)
- \(n^2 p^2 \times 2 m\)
Answer:
Angular momentum, L = Iω given, L = nP
Total kinetic energy
= \(\frac{P^2}{2 m}+\frac{L^2}{2 I}=\frac{P^2}{2 m}+\frac{n^2 P^2}{2 I}\)
= \(\frac{P^2}{2}\left(\frac{1}{m}+\frac{n^2}{I}\right)\)
It is impossible to calculate the total kinetic energy as no information is given about the moment of inertia I of the rigid body.
Besides, P = rβ and given L = nβ.
Therefore, the dimension of n is equal to the dimension of r. So, the dimension of the kinetic energy does not match with any one of the dimensions of the four options.
The question is incorrect or incomplete.
None of the options are correct.
Question 27. A thin uniform rod of mass M and length L is rotating about a perpendicular axis passing through its centre with a constant angular velocity ω. Two objects each of mass \(\frac{M}{3}\) are attached gently to the two ends of the rod. The rod will now rotate with an angular velocity of
- \(\frac{1}{3}\)ω
- \(\frac{1}{7}\)ω
- \(\frac{1}{6}\)ω
- \(\frac{1}{2}\)ω
Answer:
Initially the moment of inertia of the uniform rod, I = \(\frac{L}{2}\)ML²
After attaching the two objects, the moment of inertia, \(I^{\prime}=\frac{1}{12} M L^2+2 \times \frac{1}{3} M\left(\frac{L}{2}\right)^2=\left(\frac{1}{12}+\frac{1}{6}\right) M L^2=\frac{1}{4} M L^2\)
From the law of conservation of the angular momentum, \(I \omega=I^{\prime} \omega^{\prime}\)
or, \(\omega^{\prime}=\frac{I}{I^{\prime}} \omega=\frac{\frac{1}{12} M L^2}{\frac{1}{4} M L^2} \omega=\frac{1}{3} \omega\)
The option 1 is correct.
Question 28. The rotational kinetic energy of a solid sphere of mass 3 kg and radius 0.2 m rolling down an inclined plane of height 7 m is
- 42 J
- 60 J
- 36 J
- 70 J
Answer:
From the law of conservation of energy, initial potential energy = final translational kinetic energy + final rotational kinetic energy
∴ \(m g h=\frac{1}{2} m v^2+\frac{1}{2} I \omega^2=\frac{1}{2} m R^2 \omega^2+\frac{1}{2}\left(\frac{2}{5} m R^2\right) \omega^2\)
= \(\frac{1}{2} m R^2 \omega^2+\frac{1}{5} m R^2 \omega^2=\frac{7}{10} m R^2 \omega^2\)
Rotational kinetic energy,
= \(\frac{1}{5} m R^2 \omega^2=\frac{2}{7} \times \frac{7}{10} m R^2 \omega^2\)
= \(\frac{2}{7} m g h=\frac{2}{7} \times 3 \times 10 \times 7=60 \mathrm{~J}\)
The option 2 is correct.
Question 29. Three objects, A (a solid sphere), B (a thin circular disc) and C (a circular ring), each have the same mass M and radius R. They all spin with the same angular speed ω about their own symmetry axes. The amount of work (W) required to bring them to rest, would satisfy the relation
- WB >WA>WC
- WA>WB> WC
- WC> WB> WA
- WA>WC> WB
Answer:
Given
Three objects, A (a solid sphere), B (a thin circular disc) and C (a circular ring), each have the same mass M and radius R. They all spin with the same angular speed ω about their own symmetry axes.
The amount of work (W) required to bring the objects = change in kinetic energy (ΔEk)
For the solid sphere, \(W_A=\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{2}{5} M R^2\right) \omega^2=\frac{1}{5} M R^2 \omega^2\)
For the thin circular disc, \(W_B=\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{1}{2} M R^2\right) \omega^2=\frac{1}{4} M R^2 \omega^2\)
For the circular ring, \(W_C=\frac{1}{2} I \omega^2=\frac{1}{2}\left(M R^2\right) \omega^2=\frac{1}{2} M R^2 \omega^2\)
∴ \(W_A: W_B: W_C=\frac{1}{5}: \frac{1}{4}: \frac{1}{2}=4: 5: 10\)
Therefore, \(W_C>W_B>W_A\)
The option 3 is correct.
Question 30. A solid sphere is rotating freely about its symmetry axis in free space. The radius of the sphere is increased keeping its mass the same. Which of the following physical quantities would remain constant for the sphere?
- Rotational kinetic energy
- Moment of inertia
- Angular velocity
- Angular momentum
Answer:
Given
A solid sphere is rotating freely about its symmetry axis in free space. The radius of the sphere is increased keeping its mass the same.
⇒ \(\tau_{\text {ext }}=0\)
∴ \(\frac{d L}{d t}=0\)
Hence, L = constant
Angular momentum would remain constant for the sphere.
The option 4 is correct.
Question 31. A solid sphere is in a rolling motion. In rolling motion, a body possesses translational kinetic energy (Kt) as well as rotational kinetic energy (Kr) simultaneously. The ratio Kt:(Kt+ Kr) for the sphere is
- 10:7
- 5:7
- 7:10
- 2:5
Answer:
Given
A solid sphere is in a rolling motion. In rolling motion, a body possesses translational kinetic energy (Kt) as well as rotational kinetic energy (Kr) simultaneously.
⇒ \(K_t=\frac{1}{2} m v^2\)
⇒ \(K_r=\frac{1}{2} I \omega^2=\frac{1}{2}\left(\frac{2}{5} m r^2\right) \cdot\left(\frac{\nu}{r}\right)^2=\frac{1}{5} m v^2\)
∴ \(\frac{K_t}{K_t+K_r}=\frac{\frac{1}{2} m v^2}{\frac{1}{2} m v^2+\frac{1}{5} m v^2}\)=\(\frac{\frac{1}{2} m v^2}{\frac{7}{10} m v^2}=\frac{5}{7}\)
or, \(K_t:\left(K_t+K_r\right)=5: 7\)
The option 2 is correct.
Question 32. A solid sphere of mass m and radius r is rolling on a horizontal surface. What rotation of total energy of the sphere is: Kinetic energy of rotation? The kinetic energy of translation?
Answer:
Given
A solid sphere of mass m and radius r is rolling on a horizontal surface.
Mass of sphere = m, radius = r
Moment of inertia = \(\frac{2}{5}\)mr²
Total energy = KR + Kr
⇒ \(K_{\text {total }}=\frac{1}{2} I \omega^2+\frac{1}{2} m v^2=\frac{1}{2} \times \frac{2}{5} m r^2\left(\frac{v^2}{r^2}\right)+\frac{1}{2} m v^2\) (because v=rω)
⇒ \(K_{\text {total }}=\frac{1}{2}\left(\frac{7}{5}\right) m v^2\)
Fraction of kinetic energy of rotation
= \(\frac{K_R}{K_{\text {total }}}=\frac{\frac{1}{2}\left(\frac{2}{5}\right) m v^2}{\frac{1}{2}\left(\frac{7}{5}\right) m v^2}=\frac{2}{7}\)
Fraction of kinetic energy of translation
= \(\frac{K_T}{K_{\text {total }}}=\frac{\frac{1}{2} m v^2}{\frac{1}{2}\left(\frac{7}{5} m v^2\right)}=\frac{5}{7}\)
Question 33. Find
- The moment of inertia of a rod of mass 100 g and length 100 cm about and axis passing through its centre and perpendicular to its length and
- The radius of gyration.
Answer:
Mass of rod, M = 100 g = 0.1 kg; length, L = 100 cm = 1 m.
1. Moment of inertia about the said axis is,
I = \(\frac{1}{12} M L^2\) = \(\frac{1}{12} \times 0.1 \times 1^2\)
= \(\frac{1}{120}=8.33 \times 10^{-3} \mathrm{~kg} \cdot \mathrm{m}^2\)
2. If k is the radius of gyration, then I = Mk²
or, \(k=\sqrt{\frac{I}{M}}=\sqrt{\frac{\frac{1}{120}}{0.1}}=\sqrt{\frac{1}{12}}=0.29 \mathrm{~m}\)
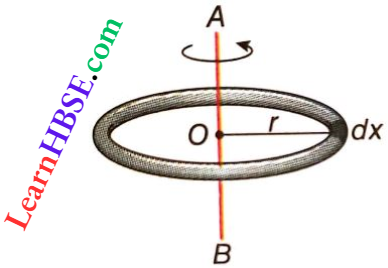
Question 34. Using it find the moment of inertia of a ring of mass m and radius r about an axis passing through the tangent to the circle of the ring.
Answer:
Let m be mass of a ring and r be its radius. Then, the moment of inertia of the ring about the axis passing through its centre and perpendicular to its plane (z-axis) is,
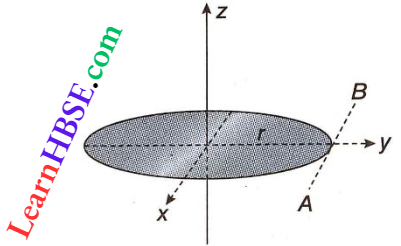
Iz = mr²
If Ix and Iy be the moments of inertia of the ring, respectively, about two perpendicular diameters on the plane of the ring (along x and y-axes), then from the perpendicular-axes theorem, \(I_z=\left(I_x+I_y\right)\)
= \(2 I_x=m r^2 \quad\left[I_x=I_y, \text { from symmetry }\right]\)
or, \(I_x=\frac{1}{2} m r^2\)
Now from the parallel-axes theorem, the moment of inertia about the axis AB, which is parallel to the x-axis and tangential to the ring, is
I = \(I_x+m r^2=\frac{1}{2} m r^2+m r^2=\frac{3}{2} m r^2\)
Question 35. Write the expression for work done in the rotational motion of an object about a fixed axis.
Answer:
Work done, dW = \(\vec{\tau} \cdot d \vec{\theta}\), where \(\vec{\tau}\) = torque about the fixed axis and \(d \vec{\theta}\) = angular displacement
Question 36. Given the moment of inertia of a disc of radius R, mass M about an axis along its diameter to be (MR²)/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge.
Answer:
Given
The moment of inertia of the disc about the x-axis lying along one of its diameters is Ix = \(\frac{1}{4}\)MR² (given).
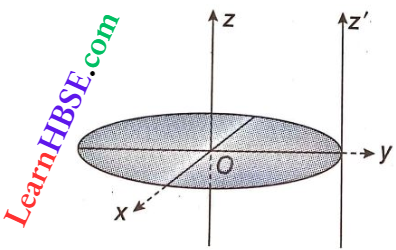
From symmetry, Iy = Ix = \(\frac{1}{4}\)MR²
From the perpendicular-axes theorem, the moment of inertia about the z-axis, passing through the centre of the disc and normal to it, is
⇒ \(I_z=I_x+I_y=2 I_x=2 \times \frac{1}{4} M R^2=\frac{1}{2} M R^2\)
So, the moment of inertia about an axis (denoted by z’) parallel to the z-axis and passing through a point on the edge of the disc, using the parallel-axes theorem, is
I = \(I_{\mathrm{cm}}+M R^2=I_z+M R^2=\frac{1}{2} M R^2+M R^2=\frac{3}{2} M R^2\)
Question 37. If no external force is acting on a two-body system, what will happen to
- The velocity of the centre of mass, and
- Angular momentum?
Answer:
- Whatever be the interaction between the two bodies, their centre of mass would remain unaffected if no external force is acting. So, if the centre of mass is at rest or in motion initially, it would continue in that state, i.e., would be at rest or in motion with a uniform velocity.
- External force = 0; so, external torque on the system = 0. Hence, the angular momentum of the system would remain conserved.
Question 38. The moment of inertia of a circular ring about its diameter is \(\frac{1}{2}\)MR². Calculate the moment of inertia of the ring about its tangent lying in its plane.
Answer:
Given, the moment of inertia of this circular ring about its diameter AB, Icm = \(\frac{1}{2}\)MR²
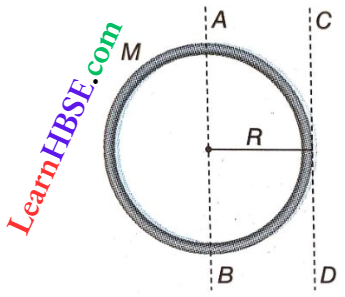
From the parallel-axes theorem, the M.I. of the ring about the tangent CD, lying in its plane, is
I = ICM + MR²
= \(\frac{1}{2}\)MR² + MR² = \(\frac{3}{2}\)MR²
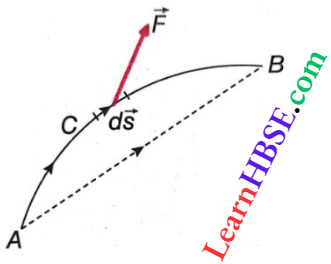
Question 39. Using the formula of torque\(\tau=x F_y-y F_x\), derive the polar formula of torque.
Answer:
Given
\(\tau=x F_y-y F_x\)
Let an external force \(\vec{F}\) act on a particle P. Suppose the line of action of \(\vec{F}\) makes an angle α with the x-axis.
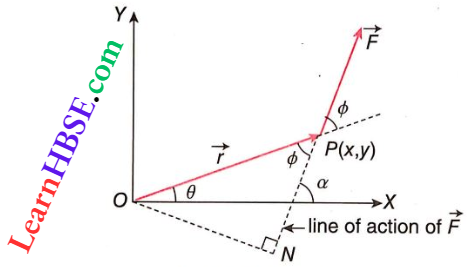
From, Fx = Fcosα…..(1)
Fy = Fsinα….(2)
If the coordinates of P are denoted by (x, y) where \(\overrightarrow{O P}\) = \(\vec{r}\) and ∠POX = θ, then
x = rcosdθ……(3)
and y = rsinθ….(4)
Putting the values of Fx, Fy, x and y in the expression of torque τ = xFy – yFx we get,
τ = rF[sinαcosθ – cosαsinθ] = rFin(α – θ) …..(5)
Let the line of action of \(\vec{F}\) make an angle ø with the position vector \(\vec{r}\).
From, θ + ø = α
or, ø = ∝ – θ…..(6)
Putting the value of ø in equation (5), τ = rFsinø
which is the expression of torque in polar coordinates.
Question 40. Calculate the moment of inertia of a ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring.
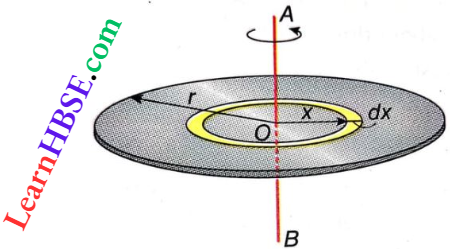
Answer:
The moment of inertia of a ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring
Let M be the mass of the ring with radius r and centre O.
Length of the ring =2πr
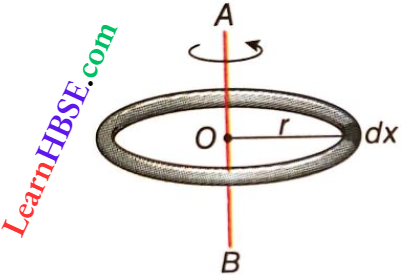
Mass per unit length of the ring = \(\frac{m}{2 \pi r}\)
Now, mass of length element dx = \(\frac{m}{2 \pi r}\) · dx
Moment of inertia of this element about the axis \(=\left(\frac{m}{2 \pi r} d x\right) r^2=\frac{m r}{2 \pi} \cdot d x\)
Hence, moment of inertia of the entire ring about the axis,
I = \(\int_0^{2 \pi r} \frac{m r}{2 \pi} d x=\frac{m r}{2 \pi} \int_0^{2 \pi r} d x\)
= \(\frac{m r}{2 \pi}(2 \pi r-0)=m r^2\)
Question 41. Derive an expression for torque in a polar coordinate system, with the help of the appropriate figure.
Answer:
An expression for torque in a polar coordinate system
Suppose the position vector of the particle at point P(x, y) is \(\vec{r}\) and it makes an angle θ with the x-axis. Let the angle between the force vector \(\vec{F}\) and position vector \(\vec{r}\) be ø. If \(\vec{F}\) makes an angle α with the positive direction of the x-axis, then
ø = α – θ
Now Fx = Fcosα and Fy = Fsinα
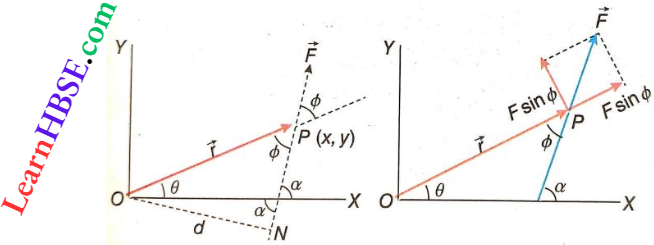
If x and y are coordinates of the point P where PO = r and ∠XOP = θ, then
x = rcosθ and y = rsinθ
We have seen that, τ = xFy – yFx…..(1)
Putting the various values in equation (1), we have,
⇒ \(\tau=(r \cos \theta)(F \sin \alpha)-(r \sin \theta)(F \cos \alpha)\)
= \(r F(\sin \alpha \cos \theta-\cos \alpha \sin \theta)\)
= \(r F \sin (\alpha-\theta)\)
= \(r F \sin \phi\) (because \(\phi=\alpha-\theta\))
τ =r F sin∅
The above expression is the expression for torciue in polar coordinates. Note that torque due to a \(\vec{F}\) force depends upon the magnitude of force and displacement (\(\vec{r}\)) of the force from the axis of rotation (point O).