Work And Energy – Elastic And Inelastic Collisions
The total momentum of a system of interacting bodies remains constant in the absence of an external force. But generally, the total kinetic energy of the system is not conserved. In most collisions, a fraction of the kinetic energy transforms into heat and sound.
- If the total momentum and the total kinetic energy of a system are conserved, the collision is termed as an elastic collision. The collision of two billiard balls on a smooth board is almost elastic. Collisions in atoms and molecules, or interactions involving protons, electrons, neutrons, etc., are assumed to be elastic.
- On the other hand, if the total momentum is conserved, but the total kinetic energy is not, it is an inelastic collision. Most practical collisions are inelastic.
Derivation Of One-Dimensional Elastic Collision Between Two Particles: Suppose m1 and m2 are the masses of two particles that are moving with velocities \(\overrightarrow{u_1}\) and \(\overrightarrow{u_2}\) respectively(ux > 1ÿ) in the same direction along a straight line. They collide elastically, and after collision, move along the same direction with velocities \(\overrightarrow{v_1}\) and \(\overrightarrow{u_2}\) respectively.
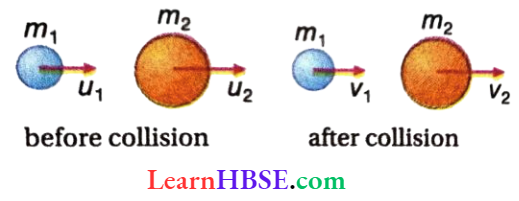
Since one-dimensional motion is considered here vector notation can be dropped. Only components can be used with signs to indicate direction.
From the law of conservation of momentum, \(m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2\)
or, \( m_1\left(u_1-v_1\right)=m_2\left(v_2-u_2\right)\)…(1)
In an elastic collision, the total kinetic energy of the particles will also be conserved.
Hence, kinetic energy before collision = kinetic energy after collision
or, \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\)
or, \(m_1\left(u_1^2-v_1^2\right)=m_2\left(v_2^2-u_2^2\right)\)…(2)
Now, (2) ÷(1) gives, \(u_1+v_1=v_2+u_2 \quad \text { or, } u_1-u_2=v_2-v_1\)…(3)
Hence, \(v_2=u_1+v_1-u_2\)
Substituting the value of \(v_2\) in equation (1) \(m_1\left(u_1-v_1\right)=m_2\left(u_1+v_1-2 u_2\right)\)
or, \(u_1\left(m_1-m_2\right)+2 u_2 m_2=v_1\left(m_1+m_2\right)\)
or, \(v_1=\frac{m_1-m_2}{m_1+m_2} u_1+\frac{2 m_2}{m_1+m_2} u_2\)
Similarly, taking the value of \(v_1\) from equation (3) and substituting it in equation (1), \(v_2=\frac{m_2-m_1}{m_1+m_2} u_2+\frac{2 m_1}{m_1+m_2} u_1\)
It is important to note that, equations (4) and (5) are symmetrical against interchange of the first and the second particles i.e., if the subscripts 1 and 2 are interchanged same equations (4) and (5) will be obtained.
Derivation Of One-Dimensional Elastic Collision Between Two Particles Special Cases:
1. Particles Are Of Equal Mass: In this case m1 = m2, hence from equations (4) and (5), v1 = u2 and v2 = u1.
Particles exchange their velocities after the collision.
2. Particles Are Of Equal Mass, And The Second Particle Is Initially At Rest: Here, m1 = m2 and u2 = 0. Hence v1 = 0 and v2= u1, from equations (4) and (5). The first particle comes to rest and the second particle gains the velocity of the first, after collision. Such events are frequent in games like billiards.
3. Particles Are Of Equal Mass, And The Second Particle Is Initially At Rest: Here, m1 = m2 and u2 = 0. Equations (4) and (5) thus change as,
⇒ \(v_1=\frac{m_1-m_2}{m_1+m_2} u_1 \text {, and } v_2=\frac{2 m_1}{m_1+m_2} u_1\)
If m1 and m2 have different values, the first particle will not stop after collision. Hence, when a striker hits a stationary coin in a game of carrom, both the striker and the coin move after collision.
Class 11 Physics Elastic and Inelastic Collision notes
4. The First Particle Is Much Heavier Than The Second Particle And The Second Particle Is Initially At Rest.
In this case, m1 >> m2 and u2 = 0.
Hence, m1 – m2 ≅ m1 + m2 ≅ m1
∴ v1 ≅ u1 and v2 ≅ 2u1
Therefore, after collision, the velocity of the first (massive) particle practically remains unchanged; but the second particle gains a velocity equal to almost twice the initial velocity of the first particle. In a collision, the velocity acquired by a body cannot be greater than twice the velocity of the collider.
5. The Second Particle Is Much Heavier Than The First And Is Initially At Rest: Here, m2 >>m1 and u2 = 0. Hence m1 -m2 ≈ -m2 and m1 + m2 ≈ m2.
Values of v1 and v2 are thus v1 ≈ -u1 and v2 = 0.
Hence, after the collision, the massive body will continue to be at rest; and the collider will recoil with the same magnitude of velocity. A collision between a tennis ball and the earth’s surface is of this type.
Work And Energy – Elastic Collisions Numerical Examples
Example 1. Two particles of equal mass moving towards each other with velocities 20 m · s-1 and 30 m · s-1 collide. If the collision is elastic, find their velocities after the collision.
Solution:
Given
Two particles of equal mass moving towards each other with velocities 20 m · s-1 and 30 m · s-1 collide. If the collision is elastic
The particles are moving towards each other. If the velocity (u1) of one is 20 m · s-1, then the velocity (u2) of the other particle is -30 m · s-1.
After the collision, suppose the velocities are v1 and v2 respectively
From the law of conservation of linear momentum, m x 20 – m x 30 = mv1 + mv2
or, v1 + v2 = -10…(1)
For elastic collision, v2 – v1 = u1 – u2
or, v2 – v1 = 20-(-30) = 50…..(2)
Solving equations (1) and (2), v1 = -30 m · s-1 and v2 = 20 m · s-1.
Difference between elastic and inelastic collision Class 11
Example 2. Three balls A, B, and C of masses m1, m2, and m3 respectively are kept at rest along a straight line. Now A moving in that straight line with velocity u1 strikes B and then B moving with velocity u2 strikes C. As a result velocity of C becomes u3. If the collisions are elastic, show that u3 ≅ 4u1, when m1 >> m2 and m2 >>m3. In case A hits C directly, will the velocity of C be higher or lower?
Solution:
Given
Three balls A, B, and C of masses m1, m2, and m3 respectively are kept at rest along a straight line. Now A moving in that straight line with velocity u1 strikes B and then B moving with velocity u2 strikes C. As a result velocity of C becomes u3. If the collisions are elastic,
Suppose A acquires a velocity v1 after collision with B. From the law of conservation of linear momentum, for collision between A and B, m1u1 = m1v1 + m2u2
or, m1(u1 – v1) = m2u2…..(1)
From the law of conservation of kinetic energy for elastic collision \(\frac{1}{2} m_1 u_1^2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 u_2^2\)
or, \(m_1\left(u_1^2-v_1^2\right)=m_2 u_2^2\)….(2)
Dividing equation (2) by (1), \(u_1+v_1=u_2 \text { or, } v_1=u_2-u_1\)
Inserting the value of \(v_1\) in equation (1), \(m_1\left(2 u_1-u_2\right)=m_2 u_2 \quad \text { or, } 2 m_1 u_1=\left(m_1+m_2\right) u_2\)
Hence, \(u_2=\frac{2 m_1}{m_1+m_2} \cdot u_1=\frac{2}{1+\frac{m_2}{m_1}} \cdot u_1\)
As \(m_1 \gg m_2, \frac{m_2}{m_1} \ll 1\); hence, \(1+\frac{m_2}{m_1} \approx 1\).
Thus, \(u_2 \approx 2 u_1\).
Similarly, for the collision of B with C, \(u_3 \approx 2 u_2\). Thus \(u_3 \approx 4 u_1\).
But, for the direct collision of A with C, the velocity gained by C, u3‘ ≈ 2u1
∴ u3‘ is less than u3.
Hence, in case of a direct collision between A and C, the speed of C will be less.
Laws of conservation in elastic and inelastic collision Class 11
One-Dimensional Inelastic Collision Between Two Particles: In an inelastic collision, the total kinetic energy is not conserved, but the total momentum is conserved.
- Two particles are moving in the same direction in a straight line with velocities u1 and u2 respectively (u1 > u2). Before the collision, the distance between the two particles will decrease, and their velocity of approach will be = (u1 – u2).
- After collision, their separation increases with time i.e., (v2 > v1), where v1 = velocity of first particle, v2 = velocity of second particle after the impact. Therefore, ( v2 – v1) = the velocity of separation.
Coefficient Of Restitution: Coefficient of restitution is defined as the ratio of the velocity with which the two bodies separate after collision to the velocity of their approach before collision,
i.e., e = \(\frac{\text { relative velocity of separation after collision }}{\text { relative velocity of approach before collision }}\)
= \(\frac{v_2-v_1}{u_1-u_2}\)…..(2)
The value of e is practically constant for two specific bodies.
Perfectly Inelastic Collision: In this type of collision the two colliding bodies stick together and move as a single body, i.e., they move with a common velocity. A perfectly inelastic collision has been shown.
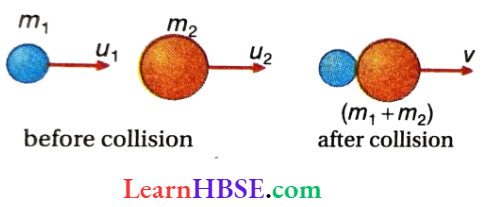
Suppose, two bodies of masses m1 and m2, moving with velocities u1 and u2 respectively in the same direction along a straight line, collide perfectly inelastically. After the collision, they stick together and move with velocity v along the same straight line.
From the principle of conservation of linear momentum, we get, \(m_1 u_1+m_2 u_2=\left(m_1+m_2\right) v\)
or, \(v^{\prime}=\frac{m_1 u_1+m_2 u_2}{m_1+m_2}\)…(2)
Perfectly Inelastic Collision Loss Of Kinetic Energy: Total kinetic energy before collision = \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2\)
Total kinetic energy after collision = \(\frac{1}{2}\left(m_1+m_2\right) v^2\)
∴ Loss of kinetic energy
= \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2-\frac{1}{2}\left(m_1+m_2\right) v^2\)
= \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2-\frac{1}{2}\left(m_1+m_2\right)\left(\frac{m_1 u_1+m_2 u_2}{m_1+m_2}\right)^2\)
= \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2-\frac{1}{2} \frac{\left(m_1 u_1+m_2 u_2\right)^2}{m_1+m_2}\)
= \(\frac{1}{2\left(m_1+m_2\right)}\)
= \(\frac{1}{2\left(m_1+m_2\right)}\) (\(m_1^2 u_1^2+m_1 m_2 u_1^2+m_1 m_2 u_2^2\))
= \(\frac{m_1 m_2}{2\left(m_1+m_2\right)}\left[u_1^2+u_2^2-2 u_1^2 u_2^2\right]\)
= \(\frac{m_1 m_2}{2\left(m_1+m_2\right)} \cdot\left(u_1 u_1^2-m_2^2 u_2^2-2 m_1 m_2 u_1 u_2 u_2\right]\)
Here (u1– u2) is the relative velocity of the two bodies before collision. So the loss of kinetic energy is proportional to the square of this relative velocity. Again if u2 = 0 i.e., if the second body is at rest before collision the loss of kinetic energy becomes maximum.
Elastic and inelastic collision Class 11 NCERT solutions
Partially Elastic Collision Definition: In this type of collision the two bodies do not stick, but move separately along the same straight line with different velocities. Here momentum remains conserved while the total kinetic energy decreases.
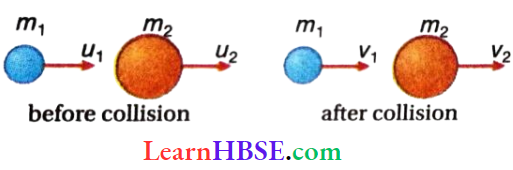
The relative velocity of the two bodies before collision = u1 – u2 and that after collision = v2 – v1.
So, the coefficient of restitution, e = \(\frac{v_2-v_1}{u_1-u_2}\)…(4)
According to the law of conservation of momentum, \(m_1 u_1+m_2 u_2=m_1 \nu_1+m_2 v_2\)…(5)
Now from equation (4) we have, \(e\left(u_1-u_2\right)=v_2-v_1\)
Multiplying the above equation by \(m_2\) we have, \(e m_2 u_1-e m_2 u_2=m_2 \nu_2-m_2 v_1\)…(6)
Subtracting equation (6) from equation (5) we get, \(u_1\left(m_1-e m_2\right)+u_2(1+e) m_2=\left(m_1+m_2\right) v_1\)
∴ \(\nu_1=\frac{\left(m_1-e m_2\right) u_1+(1+e) m_2 u_2}{m_1+m_2}\)…(7)
Similarly, \(v_2=\frac{\left(m_2-e m_1\right) u_2+(1+e) m_1 u_1}{m_1+m_2}\)
Elastic and inelastic collision Class 11 problems with solutions
Partially Elastic Collision Loss Of Kinetic Energy: \(\left(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2\right)-\left(\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\right)\)
= \(\frac{1}{2\left(m_1+m_2\right)}\left[\left(m_1+m_2\right)\left(m_1 u_1^2+m_2 u_2^2\right)-\right.\) \(\left.\quad\left(m_1+m_2\right)\left(m_1 v_1^2+m_2 v_2^2\right)\right]\)
Now, \(\left(m_1+m_2\right)\left(m_1 u_1^2+m_2 u_2^2\right)\)
= \(m_1^2 u_1^2+m_2^2 u_2^2+m_1 m_2\left(u_1^2+u_2^2\right)\)
= \(\left(m_1 u_1+m_2 u_2\right)^2+m_1 m_2\left(u_1-u_2\right)^2\)
Similarly, \(\left(m_1+m_2\right)\left(m_1 v_1^2+m_2 v_2^2\right)\)
= \(\left(m_1 v_1+m_2 v_2\right)^2+m_1 m_2\left(v_1-v_2\right)^2\)
= \(\left(m_1 u_1+m_2 u_2\right)^2+m_1 m_2 e^2\left(u_1-u_2\right)^2\)
(because \(v_2-v_1=e\) \((u_1-u_2)\))
So, the loss of kinetic energy = \(\frac{1}{2\left(m_1+m_2\right)}[\left(m_1 u_1+m_2 u_2\right)^2+m_1 m_2\left(u_1-u_2\right)^2\)
– \((m_1 u_1+m_2 u_2)^2-m_1 m_2 e^2\left(u_1-u_2\right)^2\)
= \(\frac{m_1 m_2}{2\left(m_1+m_2\right)}\left(1-e^2\right)\left(u_1-u_2\right)^2 \)…(9)
- If e = 1, i.e., if the collision is perfectly elastic, then the loss of kinetic energy = 0, i.e., in case of a perfectly elastic collision kinetic energy remains conserved.
- If e = 0 , i.e., if the collision is perfectly inelastic, kinetic energy decreases and the loss of kinetic energy = \(\frac{m_1 m_2}{2\left(m_1+m_2\right)}\left(u_1-u_2\right)^2\)
- For partially elastic collision, 0 < e < 1.
Inelastic Collisions Numerical Examples
Example 1. Two bodies of masses 5 kg and 10 kg move towards each other with velocities 10 m · s-1 and 14 m s-1 respectively. If the coefficient of restitution is 0.8, find their velocities after the collision.
Solution:
Given
Two bodies of masses 5 kg and 10 kg move towards each other with velocities 10 m · s-1 and 14 m s-1 respectively. If the coefficient of restitution is 0.8
Let u1 and u2 respectively be the velocities of the first and the second body before the collision. After the collision, their velocities will be v1 and v2 respectively.
From the law of conservation of linear momentum \(m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2\)
Here, \(m_1=5 \mathrm{~kg}, \quad m_2=10 \mathrm{~kg}, \quad u_1=10 \mathrm{~m} \cdot \mathrm{s}^{-1}\) and \(u_2=-14 \mathrm{~m} \cdot \mathrm{s}^{-1}\)
[let us assume \(u_1\) to be taken along positive x-axis and \(u_2\) along negative x-axis]
∴ \(5 \times 10+10 \times(-14)=5 v_1+10 v_2\)
or, \(v_1+2 v_2=-18\)….(1)
Also, \(e=\frac{v_2-v_1}{u_1-u_2}\) or, \(0.8=\frac{v_2-v_1}{10-(-14)}\)
or, \(v_2-v_1=0.8 \times 24=19.2\)…..(2)
Hence, from (1) and (2), \(3 v_2=1.2 \text { or, } v_2=\frac{1.2}{3}=0.4 \mathrm{~m} \cdot \mathrm{s}^{-1}\)
and \(v_1=-18.8 \mathrm{~m} \cdot \mathrm{s}^{-1}\) which means after the collision the 5 kg mass advances along the negative x-axis and the 10 kg mass goes along positive x-axis.
Real life examples of elastic and inelastic collision Class 11
Example 2. Two bodies of masses 1 kg and 0.5 kg towards each other with velocities 10 cm · s-1 and 5 cm · s-1 respectively. After the collision, the bodies coalesce (Join together). Find the common velocity after collision and the loss in kinetic energy.
Solution:
Given
Two bodies of masses 1 kg and 0.5 kg towards each other with velocities 10 cm · s-1 and 5 cm · s-1 respectively. After the collision, the bodies coalesce
Let the velocity of the combined mass after collision be v. From the law of conservation of momentum, \(m_1 u_1+m_2 u_2=\left(m_1+m_2\right)v\)
or, \(1 \times 0.1+0.5 \times(-0.05)=(1+0.5) v\)
or, \(0.1-0.025=1.5 v \quad \text { or, } v=\frac{0.075}{1.5}=0.05 \mathrm{~m} \cdot \mathrm{s}^{-1} .\)
This implies that the velocity of the combined mass is along the direction of the initial velocity of the 1kg mass.
The initial kinetic energy of the bodies = \(\frac{m_1 u_1^2}{2}+\frac{m_2 u_2^2}{2}=\frac{1}{2} \times 1 \times(0.1)^2+\frac{1}{2} \times(0.5) \times(0.05)^2\)
= \(5.625 \times 10^{-3} \mathrm{~J}\)
The final kinetic energy of the combined mass after the collision = \(\left(m_1+m_2\right) \frac{v^2}{2}\)
= \(\frac{1}{2} \times(1+0.5) \times(0.05)^2=1.875 \times 10^{-3} \mathrm{~J}\)
∴ Loss in kinetic energy = \((5.625-1.875) \times 10^{-3}=3.75 \times 10^{-3} \mathrm{~J} \text {. }\)
Elastic and inelastic collision Class 11 important questions
Example 3. A car of mass 2000 kg collides with a truck of mass 104 kg moving at 48 km • h-1. After the collision, the car rides up the truck, and the truck-car combination moves at 15 km • h-1. What was the velocity of the car before the collision?
Solution:
Given
A car of mass 2000 kg collides with a truck of mass 104 kg moving at 48 km • h-1. After the collision, the car rides up the truck, and the truck-car combination moves at 15 km • h-1
The collision is inelastic as both bodies move together after the collision. Suppose a body of mass m, moving with velocity u, collides inelastically along a straight line with a body of mass M and velocity v. After collision, the two masses combine and move with velocity V. Applying the law of conservation of momentum,
mu+Mv = (m + M)V or, mu – (m + M)V-Mv
or, u = \(\frac{m+M}{m} V-\frac{M}{m} \nu=\left(1+\frac{M}{m}\right) V-\frac{M}{m} \nu\)
Here \(m=2000 \mathrm{~kg}, \quad \nu=48 \mathrm{~km} \cdot \mathrm{h}^{-1}, \quad M=10000 \mathrm{~kg}\),
V = \(15 \mathrm{~km} \cdot \mathrm{h}^{-1}\)
∴ \(\frac{M}{m}=\frac{10000}{2000}=5\)
u = (1 + 5) x 15- 5 x 48 = 90 – 240 = -150 km · h-1
The negative sign indicates that, before the collision, the car was moving in the direction opposite to that of the truck.
Example 4. A ball of mass 100 g was thrown vertically upwards with a velocity of 49 m · s-1. At the same time another identical ball was dropped, to fall along the same path from a height of 98 m. After some time, the two balls collided and got stuck together. This combined mass then fell to the ground. How long was the combined mass in motion?
Solution:
Given
A ball of mass 100 g was thrown vertically upwards with a velocity of 49 m · s-1. At the same time another identical ball was dropped, to fall along the same path from a height of 98 m. After some time, the two balls collided and got stuck together. This combined mass then fell to the ground.
Suppose the balls collide at a height h above the ground in time t1. Analysing the upward motion of the 1st ball, we get, h = \(49 t_1-9.8 t_1^2 / 2\)…….(1)
Analysing the downward motion of the 2nd ball, we get, 98-h = \(9.8 t_1^2 / 2\)……(2)
From equations (1) and (2), 98 = 49t1 or, t1 = 2 s
At the time of the collision, let the velocity of the 1st ball be v1 and that of the 2nd ball be v2.
∴ v1 = 49 – 9.8 x 2 = 29.4 m · s-1 (upward) and
v2 = 9.8 x 2 = 19.6 m · s-1 (downward)
After the collision, let the velocity of the combined mass be V. Then according to the law of conservation of momentum, 0.1 x 29.4 – 0.1 x 19.6 = 2 x 0.1 x V [indicating downward motion with a negative sign]
or, V = 4.9 m · s-1 (upward)
From equation (1), we get, h = 49 x 2 – 9.8 x (2)²/2 = 78.4 m
If the combined mass was in motion for a time t, then from the relation h = ut+ 1/2 gt², we get,
-78.4 = 4.9t – 1/2 x 9.8 t², or, t2 – t- 16 = 0
∴ t = \(\frac{1}{2}(1 \pm \sqrt{1+4 \times 1 \times 16})\)
As t cannot be negative, we have, t = 4.53 s
Elastic and inelastic collision derivation Class 11
Example 5. A bullet of mass 50 g is fired into a wooden block of mass 2 kg resting on a smooth table surface. The bullet enters at 50 m · s-1 and gets embedded in the block. Find the final velocity of the block. Find the initial and the final kinetic energy of the block-bullet system.
Solution:
Given
A bullet of mass 50 g is fired into a wooden block of mass 2 kg resting on a smooth table surface. The bullet enters at 50 m · s-1 and gets embedded in the block.
From the law of conservation of momentum, m1v = (m1 + m2)V
or, V = \(\frac{m_1 \nu}{m_1+m_2}\)….(1)

Here, m1 = 50 g = 0.05 kg, v = 50 m · s-1 and m2 = 2 kg.
∴ The final velocity of the block, V = \(\frac{0.05 \times 50}{0.05+2}=1.22 \mathrm{~m} \cdot \mathrm{s}^{-1}\)
Initial kinetic energy of the system, \(E_i=\frac{1}{2} \times 0.05 \times 50^2=62.5 \mathrm{~J}.\)
Final kinetic energy, \(E_f=\frac{1}{2} \times(2+0.05) \times(1.22)^2=1.52 \mathrm{~J}\)
Elastic and inelastic collision Class 11 numericals
Example 6. A bullet of mass 250 g, moving with a horizontal velocity of 400 m · s-1, gets embedded in a target The target of mass 4.75 kg can move freely. Find the loss of kinetic energy due to this collision. What happens to this energy loss?
Solution:
Given
A bullet of mass 250 g, moving with a horizontal velocity of 400 m · s-1, gets embedded in a target The target of mass 4.75 kg can move freely.
Mass of the bullet, m = 250 g = 0.25 kg, the velocity of the bullet, v = 400 m · s-1, and the mass of the target, M = 4.75 kg.
After the impact, the target and the bullet both move with a velocity V (say).
From the law of conservation of momentum, mv = (M+ m)V
∴ V = \(\frac{m v}{M+m}=\frac{0.25 \times 400}{0.25+4.75}=20 \mathrm{~m} \cdot \mathrm{s}^{-1} .\)
Kinetic energy of the target and the bullet after collision = \(\frac{1}{2}(M+m) V^2=\frac{1}{2}(4.75+0.25) \times 20^2=1000 \mathrm{~J}\)
Kinetic energy of the bullet before the collision,
= \(\frac{1}{2} m v^2=\frac{1}{2} \times 0.25 \times(400)^2=20000 \mathrm{~J}\).
Hence, the kinetic energy lost in collision = 20000-1000 = 19000 J.
This kinetic energy transforms into heat and sound energy.
Collisions In Two Dimensions: Let a particle of mass m1 moving with a velocity u1 along AO, collide at point O with another particle of mass m2 moving with velocity u2 along BO. The point O is chosen as the origin, the direction of AO as the x-axis, and a perpendicular direction on the plane of AO and BO as the y-axis.
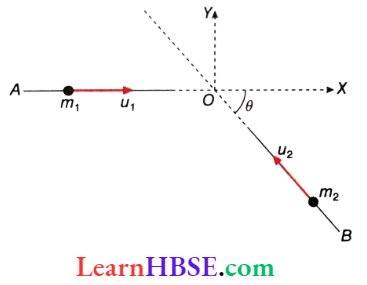
Before the collision, it is evident that, the x-component of momentum of the 1st particle = m1u1,
y -component of momentum of the 1st particle = 0,
x -component of momentum of the 2nd particle = -m2u2 cosθ,
y -component of momentum of the 2nd particle = m2u2 sinθ.
So, there is no component of momentum perpendicular to the xy-plane, i.e., along the z-direction. We know that, in both elastic and inelastic collisions, the total momentums of the particles remain conserved.
Thus, even after the collision between the two particles, there will be no z-component of momentum. This means that every two-particle collision, in general, is two-dimensional, i.e., such a collision is always confined in a plane.
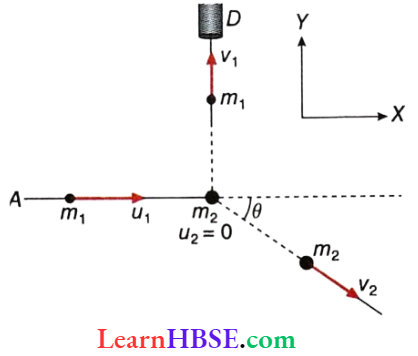
In collision experiments, usually, a beam of incident particles hits a stationary target. After the collision, the first particle is observed by placing detector D in a definite orientation, say, at right angles with the direction of the incident beam.
In the figure, m1, m2: masses of the particles; u1= velocity of m1 before collision; u2 = 0 = velocity of m2 before collision;
v1 = velocity of m1 after collision deviated by 90°;
v2 = velocity of m2 after collision;
θ = angle made by v2 with the direction of the incident beam.
Now, we may apply the principle of conservation of momentum, with the choice of the x and y-axes as shown
In the figure, x -direction: \(m_1 u_1+0=0+m_2 v_2 \cos \theta\)
or, \(m_2 v_2 \cos \theta=m_1 u_1\)…(1)
y-direction: \(0+0=m_1 v_1-m_2 v_2 \sin \theta\)
or, \(m_2 v_2 \sin \theta=m_1 v_1\)..(2)
Squaring and adding equations (1) and (2), \(m_2 v_2=m_1 \sqrt{u_1^2+v_1^2} \text { or, } v_2=\frac{m_1}{m_2} \sqrt{u_1^2+v_1^2}\)…(3)
Again, dividing equation (2) by equation (1), \(\tan \theta=\frac{v_1}{u_1} \quad \text { or, } \theta=\tan ^{-1} \frac{v_1}{u_1}\)…(4)
Usually, m1, m2, and are known prior to the experiment, and v1 is measured by the detector D. So the magnitude and direction of the velocity (v2) of the second particle after collision can be calculated using equations (3) and (4).
General Analysis Of Two-Dimensional Collisions: We have already seen that the motion of two particles, both before and after they collide with each other, is confined in a plane. Let that plane be chosen as the xy-plane. We assume that the magnitudes and the directions of the velocities (i.e., of the momenta) of the two particles, before the collision, are known beforehand.
Then, four unknown quantities, associated with the collision, are to be solved. They are the magnitudes and the directions of the velocities of the two particles after the collision.
If the collision is elastic, we can construct at most three equations from the conservation principles:
- Conservation Of Momentum Along The X-Axis,
- Conservation Of Momentum Along The Y-Axis,
- Conservation Of Kinetic Energy
These three equations are not sufficient to solve for four unknown quantities. If the collision is inelastic, the kinetic energy is not conserved. Then we have only two equations at hand. So, for a complete analysis of a two-particle collision, we should have some information on the particles after the collision.
- For example, in the collision experiment described above, we had placed a detector in such a way—at right angles to the initial direction of motion of one particle—that the final direction of the velocity of that particle was already assigned. Moreover, the detector could measure the magnitude of its velocity.
- So, we had to solve for only two unknown quantities—the magnitude and direction of the velocity of the second particle. So, only two equations were sufficient— equations obtained from the momentum conservation along the x- and the y-axes. Even the kinetic energy equation was not necessary; so the treatment was applicable to elastic as well as inelastic collisions.
- One other point is to be noted. In general, both the particles may be in motion before the collision. However, the collision may be observed by assuming one of the particles to be at rest.
The particle 2 is at rest; then the velocity of particle 1 is actually its relative velocity with respect to particle 2. This means that the frame attached to particle 2 has been taken as the frame of reference. So, there is no loss of generality if we describe a two-particle collision as a moving particle colliding with a stationary target.