Mechanical Energy
Mechanical Energy Definition: The ability of a body to do work due to its motion, position, or configuration, is called its mechanical energy.
Mechanical Energy Is Of Two Types:
- Kinetic energy and
- Potential energy.
Kinetic Energy Definition: The ability of a body to do work due to its motion is called its kinetic energy.
An external force is needed to stop a moving body. Work done by the body against the applied force till it comes to rest is equal to its initial kinetic energy.
Examples Of Kinetic Energy:
- A bullet fired from a gun can penetrate through a target, whereas a stationary bullet cannot. A high-speed bullet is able to do some work due to the kinetic energy acquired from its motion. Most of this kinetic energy is converted to heat energy.
- The wind carries a boat forward when the sails of the boat are hoisted. Wind has the ability to do work due to its motion.
- An athlete takes a long run to acquire kinetic energy, before a long jump. Using this energy, the athlete works against air friction and gravity and can cover a longer distance during the jump.
- While hammering a nail into a wall, the hammer should be brought swiftly to the nail to apply an impulsive force. The hammer acquires kinetic energy due to its rapid motion. This energy is used for doing work against the resistance of the wall on the nail, as it penetrates through the wall.
The kinetic energy of water and wind is used for different purposes, including the production of electrical energy, windmill operations, etc.
Expression Of Linear Kinetic Energy: Suppose a body of mass m moves in a straight line with velocity u. Let a constant force F be applied against the motion of the body. Hence, a retardation a is produced and after a further displacement s the body comes to rest.
So, work done against the force F until the body stops = Fs = mas…(1)
As the final velocity of the body is zero, 0 = u²-2as [using the formula, v² = u² + 2as]
or, \(a s=\frac{u^2}{2}\)….(2)
or, \(mas =\frac{m u^2}{2}\)
∴ Work done = \(\frac{1}{2} m u^2\)
This expression, 1/2 mu², is regarded as the measure of the kinetic energy (K) of a body of mass m, moving with a velocity u. It is equal to the work done to stop the motion of the body.
Hence, K = \(\frac{1}{2}\)….(3)
or, linear kinetic energy = \(\frac{1}{2}\) x mass x (linear velocity)²
If due to the application of a force, a body accelerates, its kinetic energy increases, and the opposite happens when the body decelerates.
mechanical energy class 11 notes
Relationship Between Momentum And Kinetic Energy: A body of mass m, moving with a velocity u, has a momentum, p = mu.
∴ Its kinetic energy, K = \(\frac{1}{2} m u^2=\frac{1}{2} \cdot \frac{m^2 u^2}{m}=\frac{p^2}{2 m}\).
∴ \(p^2=2 m K \quad \text { or, } p=\sqrt{2 m K}\)
Work Energy Theorem Derivation: Let m = mass of a particle, \(\vec{F}\) = force or resultant of forces, acting on the particle, \(\vec{s}\) = displacement of the particle in time t, \(\vec{v}\) = velocity of the particle at time t, and its initial and final values are vA and vB.
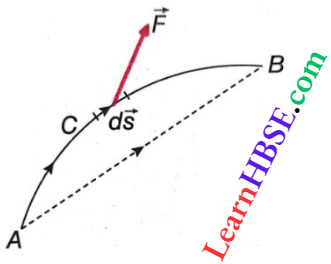
We shall consider the most general case
- The path ACB of the particle is a curved path,
- \(\vec{F}\) is a variable force, changing with time both in magnitude and in direction,
- The angle, between \(\vec{F}\) and the infinitesimal displacements d\(\vec{s}\) along the path, also varies with time.
Then, the work done for the entire motion along the path ACB is
W = \(\int_A^B \vec{F} \cdot d \vec{s}=\int_A^B m \vec{a} \cdot d \vec{s}=m \int_A^B \vec{a} \cdot d \vec{s}\)
where, \(\vec{a}=\) acceleration of the particle \(=\frac{d \vec{\nu}}{d t}\); we also know, \(\vec{v}=\frac{d \vec{s}}{d t}\)
So, W = \(m \int_A^B \frac{d \vec{v}}{d t} \cdot d \vec{s}=m \int_A^B d \vec{v} \cdot \frac{d \vec{s}}{d t}\)
= \(m \int_A^B d \vec{v} \cdot \vec{v}=m \int_A^B \vec{v} \cdot d \vec{v}\)
Now, \(\vec{v} \cdot d \vec{v} =\frac{1}{2}(\vec{v} \cdot d \vec{v}+d \vec{v} \cdot \vec{v})\)
= \(\frac{1}{2} d(\vec{v} \cdot \vec{v})=\frac{1}{2} d\left(v^2\right)\)
∴ W = \(m \int_A^B \vec{v} \cdot d \vec{v}=\frac{1}{2} m \int_A^B d\left(v^2\right)\)
= \(\frac{m}{2}\left[v^2\right]_{v_A}^{v_B}=\frac{1}{2} m\left(v_B^2-v_A^2\right)\)
or, W = \(\frac{1}{2} m v_B^2-\frac{1}{2} m v_A^2\)…(4)
i.e., work done = final K.E.- initial K.E. = change in K.E.
This is known as the work-energy theorem: the work done by the net force on a particle is equal to the change in its kinetic energy. Or, alternatively, the work done on a particle transforms into an equal amount of kinetic energy of the particle.
mechanical energy formula class 11
Kinetic Energy Due To On Explosion: in a bomb explosion, the body splits into many fragments, and these scatter in different directions. Hence, the explosion imparts kinetic energy to the fragments.
Let us assume that, a body of mass (M+ m) was initially at rest. So, initial momentum = 0. After the explosion, two fragments of masses m and M scatter off in mutually opposite directions.
Let their velocities be v and -V, respectively.
Then, final momentum = mv- MV.
From the law of conservation of momentum,
0 = \(m \nu-M V \text { or, } v=\frac{M V}{m} \text {. }\)
If velocity V of mass M is in the direction opposite to v, then \(\frac{\text { K.E. of mass } m}{\text { K.E. of mass } M}=\frac{K_1}{K_2} =\frac{\frac{1}{2} m v^2}{\frac{1}{2} M V^2}=\frac{m v^2}{M V^2}\)
= \(\frac{m}{M V^2}\left(\frac{M^2 V^2}{m^2}\right)=\frac{M}{m} .\)
Hence, kinetic energy is inversely proportional to the mass.
K1 > K2 if M>m.
This means that, after an explosion, the smaller fragments have larger amounts of K.E. If a fragment is too heavy, it remains almost stationary.
Also, \(\frac{K_1}{K_1+K_2}=\frac{M}{M+m}\) or, \(K_1=\frac{M\left(K_1+K_2\right)}{M+m}\)
or, \(K_1=\frac{M K}{M+m}\) where \(K=K_1+K_2=\) total kinetic energy of the two fragments.
Similarly, \(K_2=K_1 \cdot \frac{m}{M}=\frac{m K}{M+m}\).
Potential Energy Definition: The ability of a body to do work due to its special position or configuration, is called the potential energy of the body.
- An equilibrium position or configuration is primarily taken as the standard or reference; any other position or configuration is then termed as special position. The reference position or configuration is also called the zero state of the body.
- Some work has to be done on a body to take it from its reference state to any special state. This work is stored as potential energy in the body. When it comes back to its reference state, it can do some work using its stored potential energy.
Potential Energy Due To Change In Position: Work has to be done against gravity to lift a body above the surface of the earth. This work gets stored in the body in the form of gravitational potential energy.
- While returning to its reference position, i.e., the earth’s surface, the body can do work using this stored energy.
- As the body does work, its potential energy decreases and finally on reaching the reference position, its potential energy reduces to zero. For example
- A nail is half inserted into the ground. If a hammer is just held on the head of the nail, no further penetration takes place.
- But if the hammer is raised and allowed to fall on the nail head, the nail penetrates further into the earth, doing some work against the resistance of the earth’s surface.
- The raised hammer acquires the ability to do this work. This capacity to do work is its potential energy.
- Hydroelectric power is generated mainly using the gravitational potential energy of stored water. River water is stored by constructing a dam on it.
- The water in the reservoir has a large amount of potential energy due to its height. While flowing down through pipes, this potential energy changes to kinetic energy which is used to rotate the turbines of an electric generator.
mechanical energy class 11 important questions
Potential Energy Due To Change In Configuration: Let us consider an elastic body. The relative positions between the different parts of that body may be altered and the shape of the body changed. The work done to alter its shape gets stored as elastic potential energy.
The body spends this energy by doing work, to regain its original shape, and the process continues until the potential energy reduces to zero. For example:
- When the hairspring of a watch is wound, the work done is stored as potential energy. This energy is used to unwind the spring slowly and thus the watch works.
- However, when the spring unwinds completely and returns to its original shape, the stored potential energy becomes zero and the watch stops.
- In order to shoot an arrow from a bow, the bow string is pulled to change the natural shape of the bow.
- This stored potential energy in the bow transforms into the kinetic energy of the arrow.
- Hence, work has to be done to change the shape and size of an object; this work is stored as the potential energy of the object in its special configuration.
Gravitational Potential Energy Definition: The ability to do work imparted on a body, by raising it against gravity, is called the gravitational potential energy of the body.
To find the magnitude of the gravitational potential energy of a body, a reference plane has to be chosen. The potential energy of the body on the reference plane is taken as zero. The surface of the earth is the usual choice for the reference plane.
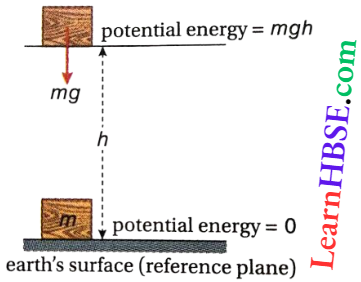
Let a body of mass m be raised to a height h from the surface of the earth (reference plane)
Force acting on the body = its weight = mg Work done against gravitational force = force x displacement = mg · h
This work done is stored as the potential energy (V) in the body.
∴ V = mgh
or, gravitational potential energy of a body = mass of the body x acceleration due to gravity x-height of the body from the reference plane
In this case, the value of g can be taken as a constant, as the height h is usually negligible compared to the radius of the earth.
mechanical energy derivation class 11
Gravitational Potential Energy Is Independent Of Path: Gravitational potential energy depends on the vertical height, but not on the actual path followed to attain that height. Let a body of mass m be raised from the earth’s surface to a height h along a frictionless plane AB of inclination θ. The weight of the body mg acts vertically downwards.
Component mg sinθ of this force along the inclined plane acts downwards and the vertical component mgcosθ acts perpendicular to the inclined surface AB. To pull the body up along the inclined surface, work has to be done against the component mgsinθ.
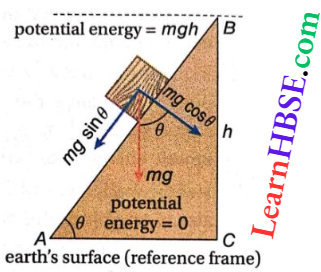
So work done to pull the body from A to B
= force x displacement
= mg sinθ x AB = mgx AB sinθ = mgx BC [AB sinθ = BC]
= mgh
Hence, the potential energy of the body at a height h above the surface of the earth = mgh.
Therefore, if the height of a body from the reference plane remains the same, the gravitational potential energy also remains the same whatever the path followed to attain that height may be.
Gravitational Potential Energy Depends On Reference Plane: For measuring the gravitational potential energy, generally, the surface of the earth is taken as the zero plane. However, the choice of this plane is totally arbitrary.
In practice, we do not measure the absolute value of the potential energy, but rather its change. Thus any convenient plane can be taken as the reference plane or zero plane. Therefore, the potential energy will be different, depending on the selection of the reference plane, even if the position of the body remains unchanged.
Gravitational Potential Energy May Be Negative: Gravitational potential energy of a body above the reference plane is positive and of that below the reference plane is negative. For example, when a body of mass m is raised from a point Q on the reference plane, to point P at a height h1, the work done is mgh1.
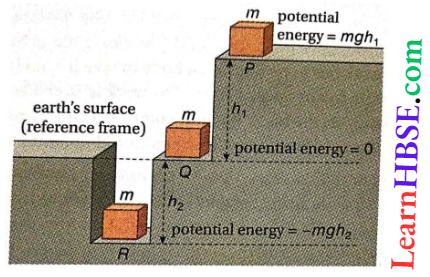
This work gets stored as potential energy and hence, the potential energy at the point P is positive. On the other hand, when the mass is taken from Q to R, a point at a depth h2 below the plane of reference, the work done is -mgh2. Hence, the potential energy at the point R is negative.
Potential Energy And Stable Equilibrium: There exists a close relationship between the potential energy and the equilibrium state of a body. An intrinsic property of a body or a system of bodies is to position itself in such a way that, its potential energy is minimal.
The equilibrium state of a body is disturbed on increasing its potential energy. Hence, water flows downwards; an extended spring regains its original configuration when released.
mechanical energy conservation class 11 physics
Elastic Potential Energy In An Extended Spring Definition: The ability of a body to do work, by virtue of its special shape, is the elastic potential energy of the body.
To extend or compress a spring, i.e., to give the spring a special shape, work has to be done against the elastic force of the material of the spring. This work remains stored in the spring as its elastic potential energy.
Let x1 = initial length of the spring, and x2 = final length on application of the stretching force.
Hence, extension in length = (x2-x1) = x (say).
Within the elastic limit, an extension of a spring is directly proportional to the stretching force applied.
∴ Applied force = k(x2 – x1), where k is a constant, called the force constant of the spring.
At the initial length x1 of the spring, the stretching force on it = 0.
Thus, for an extension of (x2 – x1) of the spring i.e., for a displacement of (x2 – x1) of the point of application of the force, an average force of [0 + k(x2 – x1)/2] or, k(x2 – x1)/2, acts on the spring.
Hence, the work done for the extension of the spring = average force x displacement
= \(\frac{1}{2} k\left(x_2-x_1\right) \times\left(x_2-x_1\right)=\frac{1}{2} k\left(x_2-x_1\right)^2=\frac{1}{2} k x^2\)
So, the potential energy of the stretched spring = \(\frac{1}{2} k x^2\)
For compression also, the potential energy stored in a spring = \(\frac{1}{2} k x^2\), where x is the change in its length.
Deduction Using Calculus Formula: When a spring is stretched in length by an amount x, an equal and opposite restoring force F is developed in the spring, and F = -kx, where k is the force constant of the spring.
When the length of the spring is further increased by dx, work done against the restoring force, dW = F · dx = kxdx [as dx is very small, F is taken as constant over this range]
Hence, the work done against the restoring force for a stretching from 0 to x0,
W = \(\int d W=\int_0^{x_0} k x d x=\frac{1}{2} k x_0^2\)
This work gets stored in the stretched spring as potential energy.
Thus, the potential energy of a stretched spring = 1/2 x force constant x (extension)².
Relation Between Work And Potential Energy: Let us consider a stone of mass m, falling freely under gravity. If we ignore air resistance, the net force acting on the stone is its weight mg, which acts downwards.
- On the other hand, the expression mgh shows that its potential energy increases with h i.e., in the upward direction. In general, the potential energy of an object increases in the direction opposite to that of the resultant force acting on it.
- When the stone is lifted from the earth’s surface, the gravitational force and displacement are in opposite directions: so, by convention, the work done by the gravitational force is negative, i.e., W = -mgh.
- At the same time, the potential energy changes from zero to mgh, i.e., the change in potential energy = mgh. So, we come to the rule that, work done = -change in P.E.
Unit 4 Work Energy Power Chapter 1 Work And Energy
Mechanical Energy Numerical Examples
Example 1. Calculate the kinetic energy of a bullet of mass 50 g moving with a velocity of 200 m · s-1.
Solution:
Kinetic energy of the bullet = \(\frac{1}{2}\) mv²
= \(\frac{1}{2}\) x 0.05 x (200)² = 103 J.
[Here, m= 50g = 0.05 kg, v = 200 m ·s-1]
mechanical energy numerical problems class 11
Example 2. A ball is moving in air at 15 m · s-1. The ball is hit with a bat and it attains a velocity of 20 m · s-1 in the opposite direction. If its kinetic energy changes by 8.75 J, what is the change in its momentum?
Solution:
Given
A ball is moving in air at 15 m · s-1. The ball is hit with a bat and it attains a velocity of 20 m · s-1 in the opposite direction. If its kinetic energy changes by 8.75 J
Change in kinetic energy of the ball, \(\Delta K=\frac{1}{2} m\left(v_2^2-v_1^2\right)\)
or, \(8.75=\frac{1}{2} m\left(20^2-15^2\right)\)
or, \(m=\frac{2 \times 8.75}{35 \times 5}=0.1 \mathrm{~kg}\)
∴ The change in momentum of the ball
= \(m\left[v_1-\left(-v_2\right)\right]=m\left(v_1+v_2\right)\)
= \(0.1(15+20)=3.5 \mathrm{~kg} \cdot \mathrm{m} \cdot \mathrm{s}^{-1} .\)
Example 3. A body of mass 10 kg falls from a height of 10 m. What will be its kinetic energy just before it touches the ground? Prove that, this kinetic energy is equal to the potential energy stored at the initial position of the body, [g = 980 cm · s-2]
Solution:
Given
A body of mass 10 kg falls from a height of 10 m.
The potential energy at the initial position =mgh = 10 x 9.8 x 10 = 980 J
Let the final velocity of the body just before it touches the ground be v.
So, v² – u² + 2gh = 0 + 2 x 9.8 x 10 = 196 m² · s-2
∴ Kinetic energy of the body just before it touches ground = \(\frac{1}{2}\)mv2 = \(\frac{1}{2}\) x 10 x 196 = 980 J
Hence, kinetic energy gained = initial potential energy.
Example 4. A force F acts on a stationary body of mass m for a time t. Show that, the kinetic energy of the body in that time = \(\frac{F^2 t^2}{2 m} \text {. }\)
Solution:
Given
A force F acts on a stationary body of mass m for a time t.
In this case, force = F; initial speed, u = 0; mass = m.
From F = ma, we can write, a = \(\frac{F}{m}\)
Also, final velocity v = u + at = \(0+\frac{F}{m} t=\frac{F}{m} t\)
∴ Kinetic energy of the body = \(\frac{1}{2} m v^2=\frac{1}{2} m\left(\frac{F}{m} t\right)^2=\frac{F^2 t^2}{2 m} \text {. }\)
Example 5. A body of mass m, starting from rest, moves with constant acceleration. After a time T it attains a velocity V. Show that the work done by the body in time t = \(\frac{1}{2} m \frac{V^2}{T^2} \cdot t^2\).
Solution:
Given
A body of mass m, starting from rest, moves with constant acceleration. After a time T it attains a velocity V.
Let the velocity attained by the body after a time t be v.
As the acceleration a is constant, V = \(a T \text { and } \nu=a t=\frac{V t}{T}\)
∴ Work done by the body = \(\frac{1}{2} m v^2=\frac{1}{2} m \frac{V^2 t^2}{T^2}\) [initial kinetic energy =0]
Example 6. A body of mass 1 kg is projected upwards with a velocity of 250 cm · s-1, from a height 8 m above the earth’s surface. What will be its kinetic energy just before it touches the ground?
Solution:
Given
A body of mass 1 kg is projected upwards with a velocity of 250 cm · s-1, from a height 8 m above the earth’s surface.
Let the speed of the body just before it touches the ground be v.
Taking the upward direction as positive,
v² = u² + 2gh = (2.5)² + 2 x 9.8 X 8
= 163.05 m² · s-2
[u = 250 cm · s-1 = 2.5 m · s-1, g = -9.8 m · s-2 and h = -8m]
∴ Kinetic energy just before it touches the ground
= \(\frac{1}{2}\) x 1 x 163.05 = 81.525 J.
principle of conservation of mechanical energy class 11
Example 7. A body of mass 5 g is moving in a straight line with a velocity of 10 cm · s-1. A force of 10√2 dyn is applied on the body at an angle of 45° with the line of motion. What is the change in kinetic energy of the body in 1st second?
Solution:
Given
A body of mass 5 g is moving in a straight line with a velocity of 10 cm · s-1. A force of 10√2 dyn is applied on the body at an angle of 45° with the line of motion.
Let the line of motion of the body be chosen as the x-axis.
Initial kinetic energy of the body
= \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) x 5 x (10)² = 250 erg
Components of the applied force along and at right angle to the direction of motion are respectively,
⇒ \(F_x=10 \sqrt{2} \cos 45^{\circ}=10 \sqrt{2} \cdot \frac{1}{\sqrt{2}}=10 \mathrm{dyn}\)
and \(F_y=10 \sqrt{2} \sin 45^{\circ}=10 \sqrt{2} \cdot \frac{1}{\sqrt{2}}=10 \mathrm{dyn}\)
∴ Components of acceleration of the body, \(a_x=a_y=\frac{F_x}{m}=\frac{F_y}{m}=\frac{10}{5}=2 \mathrm{~cm} \cdot \mathrm{s}^{-2}\)
∴ The velocity along x-axis after 1s, vx = 10 + 2 x 1 = 12cm · s-1 and along y-axis after 1s, vy =0 + 2 x 1 = 2 cm · s-1
Total kinetic energy of the body after 1s
= \(\frac{1}{2} m\left(v_x^2+v_y^2\right)\)
= \(\frac{1}{2} \times 5 \times\left(12^2+2^2\right)=\frac{1}{2} \times 5 \times 148=370 \mathrm{erg}\)
∴ Change in kinetic energy in 1 second = 370-250 = 120 erg.
Example 8. A bullet of mass 50 g, moving with a velocity of 200 m · s-1, strikes and penetrates a wooden block. If the resistance of the wooden block on the bullet is 4900 N, find the distance up to which the bullet penetrates the block.
Solution:
Given
A bullet of mass 50 g, moving with a velocity of 200 m · s-1, strikes and penetrates a wooden block. If the resistance of the wooden block on the bullet is 4900 N
Let the distance in the block that the bullet penetrates through be x.
Work done = change in kinetic energy
∴ 4900 x x =\(\frac{1}{2}\) x 0.05 x [(200)² – 0²]
∴ x = \(\frac{0.05 \times 4 \times 10^4}{2 \times 4900}=0.204 \mathrm{~m} .\)
Example 9. A bullet, of mass 50 g and of initial speed 400 m s-1, penetrates a wall against an average force of 4 x 104 N. It comes out with a speed of 50m · s-1. What is the thickness of the wall? Another bullet with a lesser mass, but with the same initial velocity, penetrates the wall but is unable to come out. What is the maximum possible mass of the second bullet?
Solution:
Given
A bullet, of mass 50 g and of initial speed 400 m s-1, penetrates a wall against an average force of 4 x 104 N. It comes out with a speed of 50m · s-1
In the first case v1 = 400 m · s-1, v2 = 50 m · s-1, F = 4 x 104 N, m = 50 g = 0.05 kg
Let the thickness of the wall be x.
Since the work done against the force is the change in kinetic energy of the bullet,
∴ \(\frac{1}{2} m\left(v_1^2-v_2^2\right)=F \cdot x \quad \text { or, } x=\frac{m\left(v_1^2-v_2^2\right)}{2 F}\)
or x = \(\frac{0.05 \times\left(400^2-50^2\right)}{2 \times 4 \times 10^4}=984.4 \times 10^{-4} \mathrm{~m}=9.844 \mathrm{~cm}\)
In the second case, let the mass of the bullet be m1.
As v2 = 0, \(\frac{1}{2} m_1 v_1^2=F \cdot x\)
∴ \(m_1=\frac{2 F \cdot x}{v_1^2}=\frac{2 \times 4 \times 10^4 \times 984.4 \times 10^{-4}}{(400)^2} \mathrm{~kg}\)
= \(492.2 \times 10^{-4} \mathrm{~kg}=49.22 \mathrm{~g}\)
Example 10. A body of mass 0.03 kg, falling from a height of 20 m, penetrates 1.5 m into the soil. Find the average resistive force of the soil.
Solution:
Given
A body of mass 0.03 kg, falling from a height of 20 m, penetrates 1.5 m into the soil.
Decrease in potential energy of the body when it comes to rest
= mgh = 0.03 x 9.8 x (20 + 1.5) = 6.32 J
Let the average resistive force of soil = F.
∴ F x 1.5 = 6.32 or, F = 4.21 N.
