Rotation Of Rigid Bodies – Relation Between Torque And Angular Acceleration
Definition Of Moment Of Interia Or Rotational Interia: When a force is applied to a body, a linear acceleration is produced in that body. Similarly, when a torque is applied to a body, an angular acceleration is produced in it. So it can be said that torque plays the same role in rotational motion as that of force in the case of linear motion. Hence, torque is the rotational analogue of force.
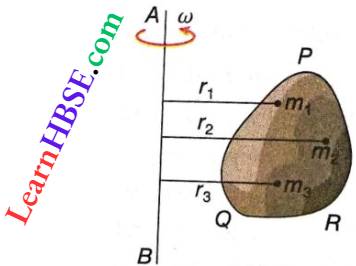
Suppose the body PQR is revolving with a uniform angular acceleration about the axis AB. The body is assumed to be made up of innumerable point masses m1, m2, m3, …, etc. These point masses are at distances r1, r2, r3, … etc. respectively from the axis of rotation AB. In the case of pure rotation, the axis of rotation remains fixed and the angular acceleration of each point mass remains the same.
But due to the difference in distances of the point masses from the axis of rotation, their linear accelerations are different. If the linear acceleration of the particle m1 is a1, then a1 = r1α and the force acting on it is F1 = m1a1 – m1r1α.
The moment of force F1 about the axis of rotation, G1 = force x perpendicular distance of the particle from the axis of rotation
⇒ \(F_1 r_1=m_1 r_1^2 \alpha\)
In this way, the moment of force can be found for every particle. The couple or torque acting on the entire rigid body is the algebraic sum of the moments of the forces acting on individual particles.
Hence, torque \(\tau=G_1+G_2+\cdots=m_1 r_1^2 \alpha+m_2 r_2^2 \alpha+\cdots\)
= \(\left(m_1 r_1^2+m_2 r_2^2+\cdots\right) \times \alpha=\sum_i m_i r_i^2\)
[mi is the mass of the i-th particle and ri is its perpendicular distance from the axis of rotation] = Iα …(1)
Here, \(I=\sum_i m_i r_i^2\)….(2)
= moment of inertia of the body about the axis of rotation
So, \(I=\frac{\tau}{\alpha}\)
i.e., moment of inertia = \(\frac{\text { torque }}{\text { angular acceleration }}\)
Relation Between Torque And Angular Acceleration Class 11
Definition Of Moment Of Inertia: A body about an axis of rotation is defined as the torque acting on the body divided by the corresponding angular acceleration thus generated about the same axis of rotation.
In calculus, equation (2) can be represented as I = \(\int r^2 d m\)…(3)
Unit And Dimension Of Moment Of Inertia:
CGS System: g · cm²
SI: kg · m²
Dimension of moment of inertia = dimension of mass x (dimension of distance)² = ML²
Some Important Points About Moment Of Inertia:
1. Moment of inertia not only depends on the mass of a body but also depends on the perpendicular distance of the particles constituting the body from the axis of rotation, i.e., on the distribution of mass of the body.
2. In case of translational motion, force = mass x acceleration (F = ma)
Again, in case of rotational motion, torque = moment of inertia x angular acceleration (τ = lα)
Hence, the equation τ = lα is the rotational analogue of the equation F = ma. Moreover, we know that rotational analogues of force and linear acceleration are torque and angular acceleration, respectively.
So, comparing the above two equations, we can say that the rotational analogue of the mass of a body is its moment of inertia. Hence, the moment of inertia in rotational motion plays the same role as the mass in the case of translational motion.
3. The moment of inertia of a rigid body about a specific axis does not depend on the total mass \(\left(M=\sum_i m_i\right)\) of the body but on the distribution of mass of the constituent particles i.e., \(\sum_i m_i r_i^2\) of the body.
As the distribution of masses from the axis of rotation changes, the moment of inertia is due to the change of the axis of rotation in its position. Except in those cases, the moment of inertia of the rigid body about a specific axis of rotation. It can safely be assumed to be a scalar quantity.
Torque And Angular Acceleration Derivation Class 11
Concept Of Moment Of Inertia: it has been said that the moment of inertia in rotational motion plays the same role as the mass in translational motion. It is evident from the following discussion.
- We know that the mass of a body in translational motion can be called its translational inertia. This is because mass is nothing but the hindrance that is generated in a body to resist any change in its translational motion.
- In the case of rotational motion, a body is compelled to change its state of motion when an external torque (rotational analogue of force) acts on it.
- In the absence of external torque, the body either remains at rest or executes uniform circular motion. It means that the moment of inertia of a body can be called its rotational inertia.
- It resists any change in the rotational motion of the body. To sum up it can be said that the relation between moment of force (torque) and moment of inertia is similar to the relation between force and mass.
- It is clear that the more the moment of inertia of a body about an axis, the more the torque necessary to rotate the body about that axis or to stop the body from rotating.
Two Important Theorems Regarding Moment Of Inertia: A regular-shaped body usually has some axis of symmetry. When the body rotates about such an axis, it undergoes just a spinning motion; during this spin, the entire body remains confined in the same region of space. A few examples of such axes of symmetry are:
- Circular Ring Or Circular Disc: The axis passing through the centre of the circle and perpendicular to its plane is the axis of symmetry.
- Sphere: Any diameter is an axis of symmetry.
- Right Circular Cylinder: The axis passing through the centres of the two circular faces is the axis of symmetry.
Now, it should be mentioned that the symmetry axis is not the only possible axis of rotation of a rigid body; a body may rotate about any other axis as well.
- For example, the diurnal motion of the earth (a sphere) is about its diameter, which is of course an axis of symmetry. In addition, the Earth rotates around the distant sun the axis of rotation passing through the sun is certainly not an axis of symmetry of the Earth. Earth has a different moment of inertia about that axis also.
- From the above discussion, it is evident that a rigid body may rotate about many possible axes. Fortunately, it is not necessary to tabulate the formulae for moments of inertia corresponding to all those axes.
- The following two theorems help us to find the moments of inertia of a body about some special axes of rotation, provided that the expression for the moment of inertia about a symmetry axis is known beforehand.
Definition Of Parallel Axis Theorem: This theorem is applicable for a body of any shape.
The moment of inertia (I) of a rigid body about any axis is equal to the sum of its moment of inertia (Icm) about a parallel axis through its centre of mass and the product of the mass (M) of the body with the square of the perpendicular distance (d) between the two axes.
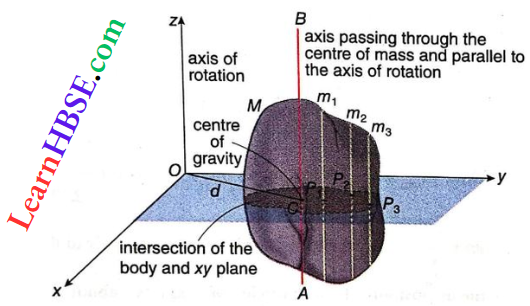
The mathematical form of the theorem, I = Icm + Md² …(1)
Torque And Angular Acceleration Formula Class 11
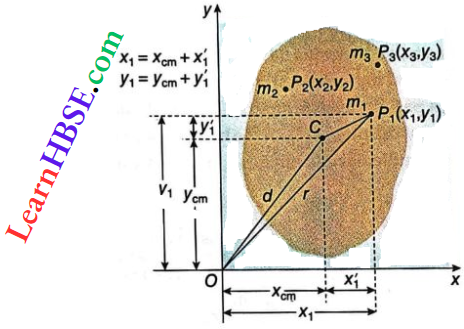
1. Parallel-Axes Theorem Explanation: Let a body is composed of an infinite number of straight-line segments parallel to the z-axis. The masses of the segments are m1, m2, m3,….. The part at which the body intercepts the xy-plane is shown.
Let, the total mass of the body M is concentrated at that intersection and mass m1 is at a distance r from the z-axis
Now, the moment of inertia of \(m_1\) about z-axis, \(I_1=m_1 r^2=m_1\left(x_1^2+y_1^2\right)\)
= \(m_1\left\{\left(x_{\mathrm{cm}}+x_1^{\prime}\right)^2+\left(y_{\mathrm{cm}}+y_1^{\prime}\right)^2\right\}\)
= \(m_1\left(x_{\mathrm{cm}}^2+y_{\mathrm{cm}}^2\right)+2 m_1\left(x_{\mathrm{cm}} x^{\prime}+y_{\mathrm{cm}} y^{\prime}\right)\) + \(m_1\left(x_1^{\prime 2}+y_1^{\prime 2}\right)\)
Therefore, the moment of inertia of the whole body about the z-axis,
I = \(\left(x_{\mathrm{cm}}^2+y_{\mathrm{cm}}^2\right) \sum m_i+2 x_{\mathrm{cm}} \sum_i m_i x_i^{\prime}\)
+ \(2 y_{\mathrm{cm}} \sum_i m_i y_i^{\prime}+\sum_i m_i\left(x_i^{\prime 2}+y_i^{\prime 2}\right) \cdots(2)\)…(2)
[where \(m_i=\) mass of the i th particle]
Now, \(\left(x_{\mathrm{cm}}^2+y_{\mathrm{cm}}^2\right)=d^2 and \sum m_i=M\).
Again \(\frac{\sum_i m_i x_i^{\prime}}{\sum_i m_i}\) and \(\frac{\sum_i m_i y_i^{\prime}}{\sum_i m_i}\) are x and y-coordinates respectively of the mean position of the particles of mass \(m_i\) about the centre of mass of the body.
∴ \(\frac{\sum_i m_i x_i^{\prime}}{\sum_i m_i}=0=\frac{\sum_i m_i y_i^{\prime}}{\sum_i m_i}\)
Hence, \(\sum_i m_i x_i{ }^{\prime}=0=\sum_i m_i y_i{ }^{\prime}\)
The last term of equation (2) is the moment of inertia of the body about A B.
Hence, \(\sum_i m_i\left(x_i^{\prime 2}+y_i^{\prime 2}\right)=I_{\mathrm{cm}}\)
∴ I = \(I_{\mathrm{cm}}+M d^2\)
Torque And Angular Acceleration Notes Class 11
2. Perpendicular Axis Theorem Definition : The moment of inertia (IZ) of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moments of inertia (Ix + Iy) of the lamina about two mutually perpendicular axes lying on the plane of the lamina and intersecting each other at the point through where the perpendicular axis passes.
The mathematical form of the theorem, Ix + Iy = Iz ….(3)
Perpendicular-Axes Theorem Explanation: Let the plane lamina be composed of an infinite number of particles and the masses of the particles are m1, m2, m3,…… Let the distance of the particle of mass m1 from the axes x, y and z be y1, x1 and d1 respectively.
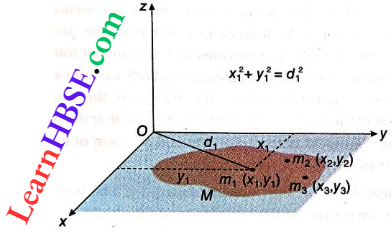
Now, the moments of inertia of the particle of mass m1 about x, y and z-axes, \(I_{x_1}=m y_1^2, I_{y_1}=m_1 x_1^2, I_{z_1}=m_1 d_1^2\)
Therefore, the moments of inertia of the whole lamina about x, y and z-axes,
⇒ \(I_x=\sum_i m_i y_i^2, I_y=\sum_i m_i x_i^2, I_z=\sum_i m_i d_i^2\)
∴ \(I_x+I_y=\sum_i m_i\left(x_i^2+y_i^2\right)=\sum_i m_i d_i^2=I_z\)
It is to be noted that this theorem of perpendicular axes is applicable only for plane sheets of small thicknesses.
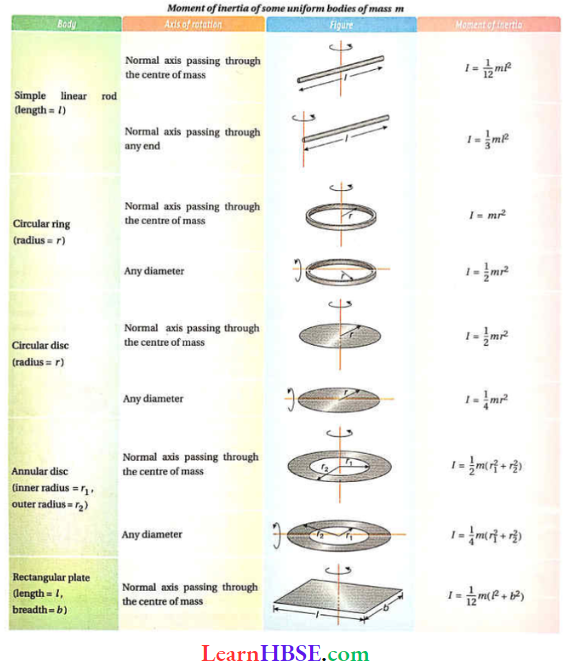
Determination Of Moment Of Inertia Of Some UniForm Symmetrical Objects:
1. Moment Of Inertia Of A Uniform Rod About The Perpendicular Axis To Its Length Passing Through Its Centre Of Mass: Let PQ be a uniform rod of mass m and length l. The centre of mass is at the midpoint O of the rod.
Considering O as the origin (0,0) and the x-axis along the length of the rod, the position coordinates of the points P and Q are (-\(\frac{1}{2}\), o) and (\(\frac{1}{2}\), o) respectively. The moment of inertia about the axis CD passing through the point O and perpendicular to the rod is to be determined.
Mass per unit length of the rod = \(\frac{m}{l}\)
Let us consider a small segment dx which is at a distance x from point O.
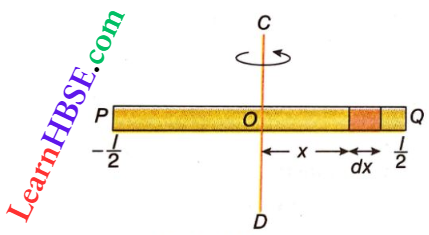
So, the mass of length dx = (\(\frac{m}{l}\)dx)
Moment of inertia of this small segment dx about CD = (\(\frac{m}{l}\)dx)x²
Hence, the moment of inertia of the whole rod about CD,
⇒ \(I_{C D}=\int_{-l / 2}^{L / 2} \frac{m}{l} x^2 d x=\frac{m}{l}\left[\frac{x^3}{3}\right]_{-\frac{l}{2}}^{\frac{l}{2}}\)
= \(\frac{m}{3 l}\left[\left(\frac{l}{2}\right)^3-\left(-\frac{l}{2}\right)^3\right]\)
= \(\left(\frac{m}{3 l} \cdot \frac{3}{4}\right)=\frac{1}{12} m l^2\)
Relation Between Moment Of Inertia And Torque Class 11
2. Moment Of Inertia Of A Uniform Rod About The Perpendicular Axis To Its Length Passing Through One End Of The Rod (Application Of Parallel-Axes Theorem): Suppose, the mass of the rod = m, length of the rod = l. Moment of inertia of A the rod about the axis CD passing through its centre of mass and perpendicular to its length, ICD = \(\frac{1}{12}\)ml²
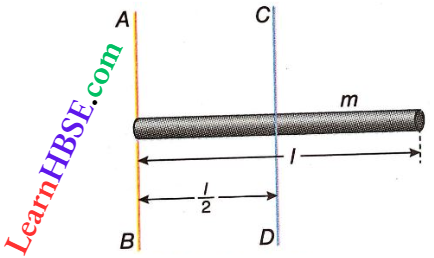
Now by the parallel axes theorem we can write,
⇒ \(I_{A B}=I_{C D}+m\left(\frac{l}{2}\right)^2\)
= \(\frac{1}{12} m l^2+\frac{1}{4} m l^2=\frac{1}{3} m l^2\)….(1)
3. Moment Of Inertia Of A Uniform Rectangular Lamina About An Axis Parallel To Its Length And Breadth Passing Through Its Centre Of Mass: Suppose, the mass of the lamina = m, length = l, breadth = b. The centre of mass of the lamina is O. The moment of inertia of the lamina about CD parallel to its breadth and passing through O is to be determined.
The mass per unit area of the rectangular lamina = \(\frac{m}{l b}\). Let us imagine a small rectangular strip of width dr at a distance r from CD
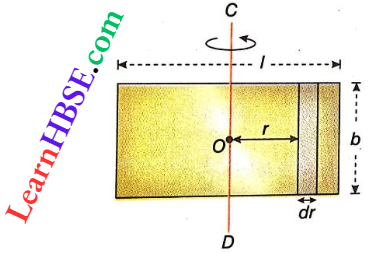
Area of this strip = bdr
Mass of this strip = bdr = \(\frac{m}{l b}\)bdr = \(\frac{m}{l}\)dr
Therefore, moment of inertia of the whole lamina about the axis parallel to its breadth and passing through the centre of mass,
Similarly, moment of inertia of the lamina about an axis parallel to its length and passing through the centre of mass, Iy = \(\frac{1}{12}\)mb²
4. Moment Of Inertia Of A Uniform Rectangular Lamina About An Axis Perpendicular To Its Plane Passing Through Its Centre Of Mass (Application Of Perpendicular-Axes Theorem): Suppose, the mass of the lamina = m; length of the lamina = l; breadth of the lamina = b
Suppose O be the centre of mass of the lamina. OX and OY are the two axes lying on the plane of the lamina, mutually perpendicular to each other. The axis OZ is perpendicular to the plane of the lamina.
We know, the moment of inertia of the lamina about an axis passing through its centre of mass and parallel to its length, Ix = \(\frac{1}{12}\)mb²
The moment of inertia of the lamina about an axis passing through its centre of mass and parallel to its breadth, Iy = \(\frac{1}{12}\)ml²
Now, by the perpendicular-axes theorem we can write, \(I_z =I_x+I_y=\frac{1}{12} m b^2+\frac{1}{12} m R^2\)
= \(\frac{1}{12} m\left(b^2+R^2\right)\)….(2)
5. Moment Of Inertia Of A Ring About An Axis Passing Through Its Centre And Perpendicular To The Plane Of The Ring: The mass of the circular ring is m and the radius of the ring is r, whose centre is O. The moment of inertia about AB passing through the point O and perpendicular to the plane of the ring to be calculated.
Let us imagine a small element of length dx on the circumference of the ring.
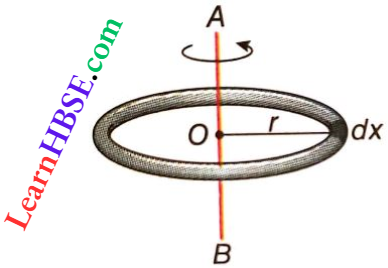
Mass per unit length of the ring = \(\frac{m}{2 \pi r}\)
Mass of that small element = \(\frac{m}{2 \pi r}\) dx
The moment of inertia of the element of length dx about AB = \(\left(\frac{m}{2 \pi r} d x\right) r^2=\frac{m r}{2 \pi} d x\)
∴ The moment of inertia of the ring about AB, \(I=\int_0^{2 \pi r} \frac{m r}{2 \pi} d x=\frac{m r}{2 \pi}[2 \pi r-0]=m r^2\)
Torque And Angular Acceleration Numericals Class 11
6. Moment Of Inertia Of A Ring About Its Diameter (Application Of Perpendicular Axes Theorem): Let AB and CD be the axes along two mutually perpendicular diameters of the ring.
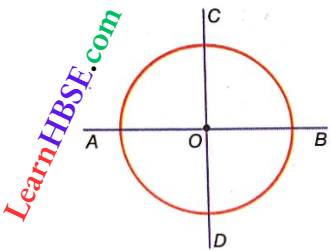
Now, by the theorem of perpendicular axes we can write, a moment of inertia of the ring about the axis AB + moment of inertia of the ring about the axis CD = moment of inertia of the ring about an axis through the centre of the ring O) and perpendicular to its plane,
i.e., IAB + ICD = mr² [where m = mass of the ring, r = radius of the ring]
For symmetry of the ring, IAB + ICD = I (say)
∴ I + I = mr² or, I = \(\frac{m r^2}{2}\) …..(3)
So, moment of inertia of a ring about its diameter = \(\frac{m r^2}{2}\)
7. Moment Of Inertia Of A Circular Disc About An Axis Passing Through Its Centre And Perpendicular To The Plane Of The Disc: P is a circular disc of mass m and radius r with centre O. The moment of inertia about AB passing through the point O and perpendicular to the plane of the disc is to be calculated.
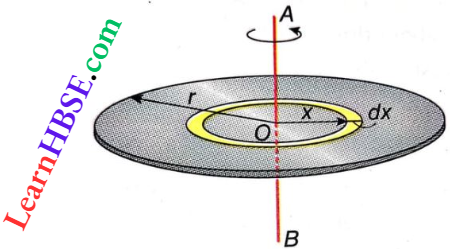
Mass per unit area of the disc = \(\frac{m}{\pi r^2}\)
Let us imagine an annular ring of width dx at a distance x (x < r) from the centre of the disc.
Area of this annular ring = \(\left(\frac{m}{\pi r^2}\right) 2 \pi x d x=\frac{2 m}{r^2} x d x\)
Therefore, a moment of inertia of this annular ring about
AB = \(\left(\frac{2 m}{r^2} x d x\right) x^2=\frac{2 m}{r^2} x^3 d x\)
Hence, moment of inertia of the whole disc about AB,
I = \(\int_0^r \frac{2 m}{r^2} x^3 d x=\frac{2 m}{r^2}\left[\frac{x^4}{4}\right]_0^r\)
= \(\frac{2 m}{4 r^2}\left[r^4-0\right]=\frac{m r^2}{2}\)
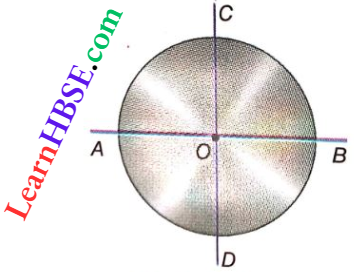
8. Moment Of Inertia Of A Circular Disc About Its Diameter (Application Of Perpendicular-Axes Theorem): Since the disc is symmetrical with respect to all diameters, its moment of inertia about every diameter is the same.
Let AB and CD be the axes along two mutually perpendicular diameters of the circular disc.
Relation Between Torque And Angular Momentum Class 11
Now, by the perpendicular-axes theorem, we can write, a moment of inertia of the disc about the axis AB + moment of inertia of the disc about the axis CD = moment of inertia of the disc about an axis through the centre of the disc O and perpendicular to its plane,
i.e., IAB + ICD = \(\frac{m r^2}{2}\)
[where, m = mass of the circular disc, r = radius of the circular disc]
For symmetry of the disc IAB + ICD = I (say)
∴ I+I= \(\frac{m r^2}{2}\)
or, \(I=\frac{m r^2}{4}\)……(4)
So, moment of inertia of a circular disc about its diameter = \(\frac{3 r^2}{4}\)
Torque And Angular Acceleration Examples Class 11
9. Moment Of Inertia Of A Circular Disc About A Tangent In The Plane Of The Disc (Application Of Parallel-Axes Theorem): Let CD be a tangent in the plane of the circular disc and AB be an axis along the diameter parallel to CD.
Let the mass of the disc be m and its radius is r.
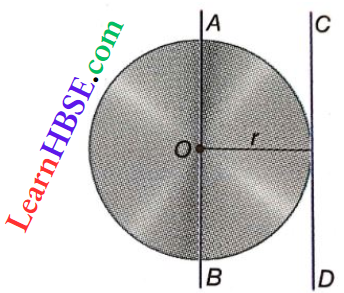
By parallel-axes theorem, we can write, a moment of inertia of the disc about CD = moment of inertia of the disc about AB+mr²
i. e., \(I_{C D}=I_{A B}+m r^2\)
= \(\frac{m r^2}{4}+m r^2\)
= \(\frac{5}{4} m r^2\)…(5)
So, the moment of inertia of a circular disc about a tangent on the plane of the disc = \(\frac{5}{4}\)[/latex]mr².
10. Moment Of Inertia Of A Circular Disc About A Tangent Perpendicular To The Plane Of The Disc (Application Of Parallel-Axes Theorem): Let CD be a tangent to the circular disc perpendicular to its plane and AB be an axis passing through the centre O of the disc and parallel to CD.
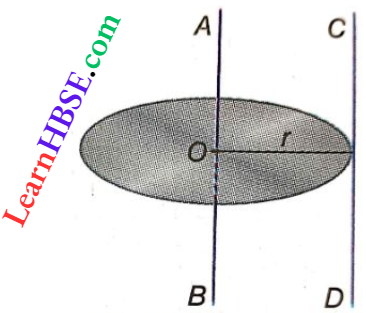
Let the mass of the disc be m and its radius is r.
By parallel-axes theorem, we can write, a moment of inertia of the disc about CD = moment of inertia of the disc about AB+mr²
i.e., \(I_{C D}=I_{A B}+m r^2\)
= \(\frac{m r^2}{2}+m r^2\)
= \(\frac{3}{2} m r^2\)….(6)
So, the moment of inertia of a circular disc about a tangent perpendicular to its plane = \(\frac{3}{2}\)mr².
Torque And Angular Acceleration Physics Class 11
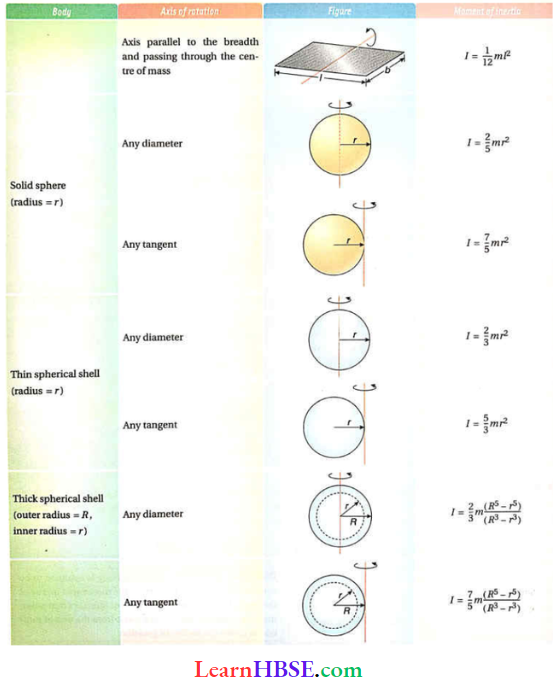

Radius Of Gyration: Notice from the above table, that in all cases moment of inertia of an extended body rotating about a specific axis depends not on total mass but on the mass distribution of the body from that very axis.
We shall now find a measuring way in which the mass of a rotating rigid body is related to the moment of inertia. For this, a new parameter, the radius of gyration (it) is introduced.
We notice that in all cases Moment of inertia can be expressed as I = Mk² form, where k has the dimension of length. ‘ k’ is a geometric property of the body and axis of rotation.
We know that if a point mass M is at a distance k from the axis of rotation, its moment of inertia, I = Mk². From this, we can define radius of gyration.
∴ k = \(\sqrt{\frac{I}{M}}\)
∴ I = Mk²
Radius Of Gyration Definition: If the whole mass of a body is assumed to be concentrated at a point such that the moment of inertia of the whole body equals the moment of inertia of that point, then the radial distance of the point from the axis of rotation is called the radius of gyration.
Radius Of Gyration Example: Moment of inertia of a solid sphere about its diameter is, I = \(\frac{2}{5}\) Mr². So, its radius of gyration with respect to its diameter,
k = \(\sqrt{\frac{\frac{2}{5} M r^2}{M}}=\sqrt{\frac{2}{5}} r\)
