Class 11 Physics Notes For Velocity Of Wave In Different Media

Wave Motion Velocity Of Sound In A Material Medium

The velocity with which sound waves will propagate in a material medium depends on two properties—density and elasticity—of the medium.

Definition Of Density In Physics: If the density of a medium is low, the effect of the pressure that a vibrating body exerts on such a medium can transmit through a large distance within a short time. On the other hand, if the density of the medium is high, the effect of pressure transmits through a comparatively small distance in equal time. Hence, the lengths of compression and rarefaction produced in a lighter medium become comparatively large and so the velocity of sound in this medium also becomes large.

Definition Of Elasticity: A vibrating particle exerts force on a medium. This results in elastic stress in the medium. Due to elastic stress, the compressed layer expands. The compressed layers of the medium which has large elasticity expand very rapidly and the expanded layers also contract very rapidly, i.e., the transformation of compression into rarefaction and vice versa takes a very short time. As a result, the velocity of sound in the medium increases.

From theoretical calculations Newton showed that the velocity of sound through a medium is given by, c = \(\sqrt{\frac{E}{\rho}}\)

where E = modulus of elasticity of the medium p = density of the medium

[As the symbol V will be used to represent volume in the next article, the velocity of sound is represented here by the symbol c.]

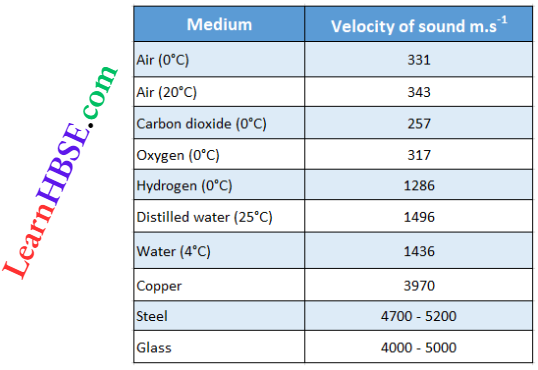
The velocity of sound in different media (at a given temperature)

Relation Between Torque And Angular Acceleration Class 11

Wave Motion Velocity Of Sound In A Gaseous Medium

Air or any gas is a material medium. So the formula of velocity of sound described in the previous section is applicable for a gas. Since gas has no length or size, the bulk modulus is the only modulus of elasticity for it. Hence, if ρ is the density of the gas, k is the bulk modulus, then the velocity of sound through the gas is given by,

c = \(\sqrt{\frac{k}{\rho}}\)…(1)

Newton’s Calculation: Sound wave propagates through a gaseous medium by the mechanism of formation of alternate layers of compression and rarefaction.

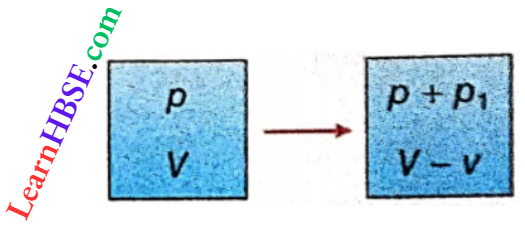
Newton assumed that propagation of sound through a gaseous medium is an isothermal process, i.e., successive compressions and rarefactions occur at such a rate that the temperature of the gaseous medium remains constant during the propagation though the pressure and volume of the gaseous medium may change.

Let the pressure and the volume of a particular amount of gas in a portion of the gaseous medium be p and V respectively.

During propagation of sound, suppose the pressure of this portion increases to p + p₁, and p₁ is very small with respect to p. As a result, its volume decreases to V- v, where v is very small with respect to V. So if the temperature remains constant, according to Boyle’s law we can write,

pV = \(\left(p+p_1\right)(V-v)=p V+p_1 V-p v-p_1 v\)

or, \(0=p_1 V-p v\)

[neglecting the term \(p_1 v\) which is very small]

or, \(\frac{p_1 V}{v}\)=p

or, \(p=\frac{p_1}{\frac{v}{V}}=\frac{\text { volume stress }}{\text { volume strain }}\)

So, bulk modulus, k = \(\frac{\text { volume stress }}{\text { volume strain }}\) = p

Proof By Calculus: According to Boyle’s law, pV = constant

On differentiation we have,

pdV + Vdp = 0 or p = \(\frac{-V d p}{d V}=-\frac{d p}{\frac{d V}{V}}\)

[the negative sign indicates that if pressure increases volume decreases]

∴ p = \(\frac{\text { volume stress }}{\text { volume strain }}\) = bulk modulus of the gas = k

So, from equation (1) we get,

Velocity of sound in a gaseous medium, c = \(\sqrt{\frac{p}{\rho}}\)…(2)

To understand how far this formula is correct, we can calculate the velocity of sound in air with this formula.

We know that standard atmospheric pressure = 76 cmHg = 76 x 13.6 x 980 dyn · cm^-2

and density of air at SIP = 0.001293 g · cm^-3

Therefore, the velocity of sound in air at STP according to Newton’s formula is

c = \(\sqrt{\frac{76 \times 13.6 \times 980}{0.001293}}=28000 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

= \(280 \mathrm{~m} \cdot \mathrm{s}^{-1} \text { (approx) }\)

However, it is found by different experiments that the velocity of sound in air at 0°C is 332 m · s^-1 (approx). From this, it can be concluded that there is a defect in Newton’s formula for determining the velocity of sound, in a gaseous medium.

Torque And Angular Acceleration Derivation Class 11

Laplace Correction Derivation: Scientist Laplace first pointed out that the propagation of sound waves through a gaseous medium takes place under adiabatic conditions and not under isothermal conditions as assumed by Newton.

According to Laplace’s assumption, compressions and rarefactions occur so quickly that the temperature of a gas cannot remain constant. On the other hand, the beat exchange does not take place among different portions of the gas during that small time interval.

As a result, the temperature of gaseous layers increases and decreases during the propagation of sound—the process is essentially adiabatic.

Now, the relation between pressure (p) and volume (V) of a. gas under adiabatic conditions is given by

pV^γ = constant

Here, \(\gamma=\frac{\text { molar specific heat of the gas at constant pressure }\left(C_p\right)}{\text { molar speciffic heat of the gas at constant volume }\left(C_v\right)}\)

Let the initial pressure and volume of a fixed amount of gas be p and V respectively. During the propagation of sound, pressure increases to p+p₁, whereas volume decreases to V-v. Here, p₁ is very small with respect to p and v is very small with respect to V.

So we write, \(p V^\gamma=\left(p+p_1\right)(V-\nu)^\gamma=\left(p+p_1\right) \cdot V^\gamma\left(1-\frac{\nu}{V}\right)^\gamma\)

or, p = \(\left(p+p_1\right)\left(1-\frac{\nu}{V}\right)^\gamma=\left(p+p_1\right)\left(1-\gamma \frac{\nu}{V}\right)\)

[neglecting other terms of binomial expansion]

= \(p+p_1-\frac{p \gamma \nu}{V}-\frac{p_1 \gamma \nu}{V}\)

or, \(p_1=\frac{\gamma p v}{V}\)….(1)

(neglecting the term \(\frac{p_1 \gamma \nu}{V} \text { as } p_1 \nu\) is very small)

∴ \(\gamma p=\frac{p_1}{\frac{v}{V}}\) = bulk modulus of the gas (k)

Hence, the bulk modulus of the gas, k = γp.

Torque And Angular Acceleration Formula Class 11

Proof By Calculus: The relation between pressure (p) and volume (V) of a gas under adiabatic condition is given by pV^ϒ = constant

On differentiation we have, \(V^\gamma d p+\gamma p^\gamma V^{\gamma-1} d V=0\)

or, \(d p+\frac{\gamma p d V}{V}=0\)

or, \(\gamma p=\frac{-d p}{\frac{d V}{V}}\)= bulk modulus of the gas (k)

So, from equation (1) we get, the velocity of sound in a gaseous medium, c = \(=\sqrt{\frac{\gamma p}{\rho}}\)….(2)

Using Laplace’s correction, the velocity of sound in air at STP,

c = \(\sqrt{\frac{1.4 \times 76 \times 13.6 \times 980}{0.001293}} \text { [for air, } \gamma=1.4 \text { ] }\)

= \(33117 \mathrm{~cm} \cdot \mathrm{s}^{-1}=331.2 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

This value of c Is very close to the experimental value of the velocity of sound in air. So we can come to the conclusion that Laplace’s equation for velocity of sound in a gaseous medium is correct.

Effect of Pressure, Temperature, Humidity, and Density of a Gas on the Velocity of Sound:

According to Laplace’s equation, if c is the velocity of sound in a gas of density ρ and pressure p, c = \(\sqrt{\frac{\gamma p}{\rho}}\)…(1)

Here γ is the ratio of the two molar-specific heats (at constant pressure and constant volume) of the gas. Now if 1 mol of gas is taken, mass = M, density \(\rho=\frac{M}{V}\)

and pV = RT (T = absolute temperature of the gas, R = universal gas constant)

So from equation (1) we get,

c = \(\sqrt{\frac{\gamma p}{\frac{M}{V}}}=\sqrt{\frac{\gamma p V}{M}}=\sqrt{\frac{\gamma R T}{M}}\)….. (2)

(Here, M = mass of 1 mol of gas, i.e., M is the molecular mass of the gas)

Effect Of Pressure: γ, R, and M are constants for a particular gas. So from equation (2) it is understood that, if the temperature of the gas remains constant, the velocity of sound does not change with a change in pressure, i.e., the pressure of the gas has no effect on the velocity of sound.

It can also be explained in a different way. At constant temperature, if the pressure of a gas is changed, the density of the gas also changes due to a change of the volume in such a way that the ratio \(\frac{p}{\rho}\) remains constant. So from equation (1) it can be said that the velocity of sound (c) remains constant with the change in pressure.

Torque And Angular Acceleration Notes Class 11

Effect Of Temperature: For a particular gas γ, R, and M—these three quantities are constants. So from equation (2) we get, c ∝ √T, i.e., the velocity of sound in the gas is directly proportional to the square root of its absolute temperature.

If c₁ and c₂ are the velocities of sound in the gas at absolute temperatures T₁ and T₂, then \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}\)

Let, \(T_1=0^{\circ} \mathrm{C}=273 \mathrm{~K}, T_2=t^{\circ} \mathrm{C}=(273+t) \mathrm{K}\)

If the velocities of sound at these two temperatures are \(c_0\) and c, then \(\frac{c_0}{c}=\sqrt{\frac{273}{273+t}}\)

or, \(c=c_0 \sqrt{\frac{273+t}{273}}=c_0\left(1+\frac{t}{273}\right)^{1 / 2} \approx c_0\left(1+\frac{1}{2} \cdot \frac{t}{273}\right)\)

= \(c_0(1+0.00183 t)\)

∴ c = \(c_0(1+0.00183 t)\)….(3)

The change of the velocity of sound due to any change in the temperature of the gas can be calculated with the help of equation (3).

Velocity of sound in air at 0°C, c₀ = 332 m · s^-1

So, c = 332(1 +0.00183t) = (332 + 0.61t) m · s^-1

Therefore, the velocity of sound in air increases by 0. 61 m · s^-1 or 61 cm · s^-1 for 1°C rise In temperature (61 cm · s^-1 ≈ 2ft · s^-1).

Effect Of Humidity: The density of water vapor is less (approximately 0.622 times) than the density of dry air at the same temperature and pressure. So if water vapor is mixed in the air, the density of air decreases. Hence, the velocity of sound in air increases, i.e., the velocity of sound in moist air is greater than that in dry air.

Let temperature of air = t°C; atmospheric pressure = p;

The velocity of sound in dry air at t°C = c;

The velocity of sound in moist air at t°C = c_m

Vapor pressure at that temperature = f

It can be shown from theoretical analysis that

c = \(c_m\left(1-0.378 \frac{f}{p}\right)^{1 / 2} \approx c_m\left(1-0.189 \frac{f}{p}\right)\)…(4)

Any experiment for determination of the velocity of sound is made in the normal atmosphere which is more or less humid. So, the velocity of sound determined by the experiment is the velocity of sound in moist air i.e., c_m. Thus tire velocity of sound in dry air, i.e., c can be obtained by using equation (4).

Relation Between Torque And Angular Momentum Class 11

Effect Of Density: Let two different gases be at the same temperature and pressure. Under this condition, if ρ₁ and ρ₂ are the densities of the two gases and c₁ and c₂ are the velocities of sound in the two gases,

⇒ \(c_1=\sqrt{\frac{\gamma p}{\rho_1}} ; c_2=\sqrt{\frac{\gamma p}{\rho_2}}\)

[It has been assumed that both the gases have the same γ]

So, \(\frac{c_1}{c_2}=\sqrt{\frac{\rho_2}{\rho_1}} \quad \text { i.e., } c \propto \frac{1}{\sqrt{\rho}}\)

Therefore, the velocity of sound in a gas is inversely proportional to the square root of its density.

For example, oxygen is 16 times, heavier than hydrogen. So velocity of sound in oxygen is \(\frac{1}{\sqrt{16}}\), i.e., \(\frac{1}{4}\) times the velocity of sound in hydrogen.

In the above discussion, γ of both gases has been taken to be equal. If each molecule of the two gases contains the same number of atoms, the values of γ for both are the same. Again if a different number of atoms are present in the molecules, corresponding values of γ are to be put in the formula.

Motion Velocity Of Sound In A Gaseous Medium Numerical Examples

Example 1. The velocity of sound in a gas at 51°C is 340 m · s^-1. What will be the velocity of sound if pressure is doubled and temperature becomes 127°C?
Solution:

Given

The velocity of sound in a gas at 51°C is 340 m · s^-1.

The pressure of the gas has no effect on the velocity of sound.

In this case velocity of sound will change only due to the change in temperature.

Initial temperature, T₁ = 51°C = (273 + 51) K = 324 K

Final temperature, T₂ = 127°C = (273 + 127) K = 400 K

We know that the velocity of sound in a gas is directly proportional to the square root of its temperature, i.e., c ∝√T.

∴ \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}\)

or, \(c_2=c_1 \sqrt{\frac{T_2}{T_1}}=340 \times \sqrt{\frac{400}{324}}\)

= \(340 \times \frac{20}{18}=378 \mathrm{~m} \cdot \mathrm{s}^{-1} \text { (approx.). }\)

Relation Between Moment Of Inertia And Torque Class 11

Example 2. The velocity of sound in a gas at 50°C is 340 m · s^-1. What will be the velocity of sound if pressure is doubled and temperature becomes 125°C?
Solution:

Given

The velocity of sound in a gas at 50°C is 340 m · s^-1.

The velocity of sound does not depend on the pressure of the gas.

Initial temperature, T₁ = 50°C = (50 + 273) K – 323 K

Final temperature, T₂ = 125°C = (125 + 273) K = 398 K

Now, velocity of sound, c ∝ √T,

i.e., \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}\)

or, \(c_2=c_1 \times \sqrt{\frac{T_2}{T_1}}=340 \times \sqrt{\frac{398}{323}}=377.4 \mathrm{~m} \cdot \mathrm{s}^{-1}\).

Example 3. Determine the velocity of sound in hydrogen at STP. At STP, density of the gas = 0.09 g L^-1; γ = 1.4
Solution:

Density, \(\rho=0.09 \mathrm{~g} \cdot \mathrm{L}^{-1}=\frac{0.09}{1000} \mathrm{~g} \cdot \mathrm{cm}^{-3}\)

= \(0.09 \times 10^{-3} \mathrm{~g} \cdot \mathrm{cm}^{-3}\)

Standard pressure, p = 76 x 13.6 x 980 dyn · cm^-2

Therefore, velocity of sound,

c = \(\sqrt{\frac{\gamma p}{\rho}} =\sqrt{\frac{1.4 \times 76 \times 13.6 \times 980}{0.09 \times 10^{-3}}}\)

= \(125525 \mathrm{~cm} \cdot \mathrm{s}^{-1}=1255.25 \mathrm{~m} \cdot \mathrm{s}^{-1} .\)

Torque And Angular Acceleration Numericals Class 11

Example 4. The ratio of γy of oxygen and methane is 21:20. The ratio of their densities at the same pressure is 2:1. lf the velocity of sound in oxygen is 316 m · s^-1, what is the velocity of sound in methane?
Solution:

Given

The ratio of γy of oxygen and methane is 21:20. The ratio of their densities at the same pressure is 2:1. lf the velocity of sound in oxygen is 316 m · s^-1,

If the velocities of sound in oxygen and methane are c₁ and c₂ respectively, then

⇒ \(c_1=\sqrt{\frac{\gamma_1 p}{\rho_1}}\) and \(c_2=\sqrt{\frac{\gamma_2 p}{\rho_2}}\)

∴\(\frac{c_1}{c_2}=\sqrt{\frac{\gamma_1}{\gamma_2} \times \frac{\rho_2}{\rho_1}}\)

or, \(c_2=c_1 \sqrt{\frac{\gamma_2}{\gamma_1} \times \frac{\rho_1}{\rho_2}}=316 \times \sqrt{\frac{20}{21} \times \frac{2}{1}} \approx 436 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Example 5. At what temperature the velocity of sound in nitrogen will be equal to its velocity in oxygen at 27°C?
Solution:

Since nitrogen and oxygen are both diatomic gases, the values of γ for both of them are equal.

The molecular mass of nitrogen, M₁ = 28

The molecular mass of oxygen, M₂ = 32

Velocity of sound, c = \(\sqrt{\frac{\gamma R T}{M}}\)

So, velocity of sound in nitrogen, \(c_1=\sqrt{\frac{\gamma R T_1}{M_1}}\)

velocity of sound in oxygen, c₂ = \(\sqrt{\frac{\gamma R T_2}{M_2}}\)

According to the question, c₁= c₂ and T₂ = 27°C = (273 + 27) K = 300 K

So, \(\sqrt{\frac{\gamma R T_1}{28}}=\sqrt{\frac{\gamma R \times 300}{32}}\)

or, \(T_1=\frac{300 \times 28}{32}=262.5 \mathrm{~K}=(262.5-273)^{\circ} \mathrm{C}\)

= \(-10.5^{\circ} \mathrm{C}\)

Torque And Angular Acceleration Examples Class 11

Example 6. The velocity of sound In hydrogen at 0tJC Is 1200 m · s^-1. If a certain amount of oxygen Is mixed with hydrogen, the velocity of sound decreases and becomes 500 m · s^-1, What Is the ratio of the volumes of hydrogen and oxygen In the mixture? It Is given that the density of oxygen Is 16 times that of hydrogen.
Solution:

Given

The velocity of sound In hydrogen at 0tJC Is 1200 m · s^-1. If a certain amount of oxygen Is mixed with hydrogen, the velocity of sound decreases and becomes 500 m · s^-1

We know, velocity of sound, c = \(\sqrt{\frac{\gamma p}{\rho}}\)

In case of hydrogen, 1200 = \(\sqrt{\frac{\gamma p}{\rho_1}}\)

In case of the given mixture, 500 = \(\sqrt{\frac{\gamma p}{\rho_2}}\)

∴ \(\frac{1200}{500}=\sqrt{\frac{\rho_2}{\rho_1}} \text { or, } \frac{\rho_2}{\rho_1}=\left(\frac{12}{5}\right)^2=\frac{144}{25}\)

Now if x volume of oxygen is mixed with 1 volume of hydrogen, the density of the mixture is given by,

⇒ \(\rho_2=\frac{1 \times \rho_1+x \times 16 \rho_1}{1+x}\)

or, \(\frac{\rho_2}{\rho_1}=\frac{1+16 x}{1+x}\)

∴\(\frac{1+16 x}{1+x}=\frac{144}{25}\)

or, \(25+400 x=144+144 x \quad \text { or, } 256 x=119\)

or, x = \(\frac{119}{256}\)

Hence, the ratio of the volumes of hydrogen and oxygen: 1 : (119/256) =256:119.

Example 7. What Is the velocity of sound in air saturated with water vapor at 27° C? It Is given that the velocity of sound in dry air at 0°C Is 332 m · s^-1 and aqueous tension at 27°C is 11.2 mmHg.
Solution:

The velocity of sound in dry air at 27°C,

c = 332(1 + 0.00183 x 27) = 332 x 1.05 m · s^-1

Aqueous tension at that temperature, f = 11.2 mm Hg = 1.12 cm Hg

If c_m is the velocity of sound in air saturated with water vapor at 27°C,

c = c_m(1-0.189 \({p}{f}\))= \(c_m\left(1-0.189 \times \frac{1.12}{76}\right)\)

= \(c_m \times 0.997\)

or, \(c_m=\frac{c}{0.997}=\frac{332 \times 1.05}{0.997}=350 \mathrm{~m} \cdot \mathrm{s}^{-1} (approx.).\)

Example 8. The velocity of sound In helium gas at -173°C is 582 m · s^-1, If the molecular mass of helium is 4, find the value of γ for the gas. (R = 8.31 x 10⁷ erg · mol^-1 · °C^-1)
Solution:

T = -173°C = (-173 + 273)K = 100K

The molecular mass of helium, M = 4

Velocity of sound, c = 582 m · s^-1 = 58200 cm · s^-1

Now, c = \(\sqrt{\frac{\gamma R T}{M}} \text { or, } \gamma=\frac{c^2 M}{R T}=\frac{(58200)^2 \times 4}{8.31 \times 10^7 \times 100}=1.63 \text {. }\)

Torque And Angular Acceleration Physics Class 11

Example 9. At STP, the velocity of sound in oxygen Is 317 m · s^-1. What is the velocity of sound In hydrogen at 30°C temperature and 374 mmHg pressure?
Solution:

At 0°C or 273 K, the velocity of sound in oxygen, c₁ =317 m · s^-1

Let c₂ be the velocity of sound in oxygen at 30°C or 303 K.

Now, \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}} \quad \text { or, } c_2=c_1 \times \sqrt{\frac{T_2}{T_1}}\)

Again at the same temperature, the velocity of sound in two gases is inversely proportional to the square root of their densities. So, if c₂‘ is the velocity of sound in hydrogen at 30°C,

∴ \(\frac{c_2{ }^{\prime}}{c_2}=\sqrt{\frac{\rho}{\rho^{\prime}}} \text { or, } c_2{ }^{\prime}=c_2 \times \sqrt{\frac{\rho}{\rho^{\prime}}}\)

∴ \(c_2{ }^{\prime}=317 \times \sqrt{\frac{303}{273}} \times \sqrt{\frac{16}{1}}=1336 \mathrm{~m} \cdot \mathrm{s}^{-1} \text { (approx.) }\)

The velocity of sound does not depend on the pressure of the gas. So, this velocity will remain the same at 374 mmHg pressure.

Example 10. The masses of 1L of hydrogen and 1L of air are 0.0896 g and 1.293 g respectively at the same temperature and pressure. If the velocity of sound In air at that temperature Is 330 m · s^-1, what will be the corresponding velocity In hydrogen?
Solution:

Given

The masses of 1L of hydrogen and 1L of air are 0.0896 g and 1.293 g respectively at the same temperature and pressure. If the velocity of sound In air at that temperature Is 330 m · s^-1

We know, the velocity of sound in a gas, c = \(\sqrt{\frac{\gamma p}{\rho}} .\)

γ = 1.41 for both hydrogen and air. If the velocities of sound in hydrogen and air at the same temperature and pressure are c_H and c_air respectively,

⇒ \(\frac{c_{\mathrm{H}}}{c_{\text {air }}}=\sqrt{\frac{\rho_{\text {air }}}{\rho_{\mathrm{H}}}}\)

or, \(c_{\mathrm{H}}=c_{\text {air }} \times \sqrt{\frac{\rho_{\text {air }}}{\rho_{\mathrm{H}}}}=330 \times \sqrt{\frac{1.293}{0.0896}}=1253.6 \mathrm{~m} \cdot \mathrm{s}^{-1} .\)