Wave Motion Echo
Definition Of Echo: We know from practical experiences that the sound produced by drums, crackers, gunshots, etc., reaches our ears directly, and also produces echoes after getting reflected from faraway buildings, trees, etc.
Echoes are distinct only when the distance between the listener and the reflecting surface is sufficiently large to allow the reflected sound to reach the listener without overlapping with the original sound.
Minimum Distance Of The Reflector
Inarticulate Sound: Echoes are produced due to the reflection of sound. But all reflected sounds cannot produce an echo. When we hear an inarticulate sound, its sensation persists in our ear for about \(\frac{1}{10}\)th of a second.
- This is known as the persistence of hearing. So to distinguish echo from the original sound, at least \(\frac{1}{10}\)th of a second should be elapsed between the production of sound and the arrival of the reflected sound in the ear-this is the condition required to hear an echo of inarticulate sound.
- We know that the velocity of sound at 0°C in air is about 330 m · s-1. So, distance travelled by sound in \(\frac{1}{10}\)s is 330 x \(\frac{1}{10}\) = 33 m. Hence, in order to hear an echo, the minimum distance between the reflecting surface and the listener should be \(\frac{33}{2}\) = 16.5 m = 54 ft. This calculation is valid for inarticulate sounds, like the sound produced by a gunshot, clapping, etc.
- If the distance of the reflector from the listener is less than 16.5 m or 54 ft, sound takes less than \(\frac{1}{10}\)s to come back to the listener after reflection. So, the listener cannot distinguish between the original sound and the reflected one, i.e., the echo is not heard. For this reason, echo is not audible in a room of ordinary size.
Wave Motion And Echo Class 11 Notes
Articulate Sound: To hear an echo of articulate sound, the minimum distance between the reflector and the listener is greater. This is due to the fact that a man cannot distinctly pronounce more than 5 syllables in one second. Our ears also cannot recognize separately more than 5 syllables in one second.
- So, for monosyllabic sound, the time interval between the original sound and its echo must not be less than \(\frac{1}{5}\)s During this time, sound travels (330 x \(\frac{1}{5}\)) or 66 m.
- This distance is again twice the distance between the listener and the reflector. So the minimum distance of the listener from the reflector should be \(\frac{66}{2}\) = 33 m, for bearing the echo of a monosyllabic word. For a disyllabic word, the distance should be 2 x 33 = 66 m, and so on.
Wave Motion Class 11 Physics Notes
Multiple Echoes: When a sound is reflected from a number of suitably placed reflecting surfaces, a number of echoes may be heard. Minimum \(\frac{1}{10}\)s of time interval is required between die original sound and the first echo and also between any two successive echoes that reach our ears.
The rumbling and rolling of under is really caused by multiple reflections from cloud surfaces. Successive reflections may also be produced between two reflecting surfaces suitably placed.
Reverberation: It is often noted that when a loud sound is produced near the walls of a big hall, it returns after reflection very quickly (i.e., the time interval is less than \(\frac{1}{10}\)s) when the effect of the original sound still persists. On account of successive reflections from the walls, a continuous rolling of sound goes on for some time. This persistence of sound due to multiple reflections from the walls is called reverberation.
- This effect is not at all desirable sometimes, because the original sound cannot be recognized distinctly. This effect is minimized by increasing the absorption of sound at the walls by carpeting them with sound-absorbing substances.
- It is obvious that if there are multiple reflectors, either echo or reverberation of sound will be produced. If the time interval between successive sounds is greater than \(\frac{1}{10}\)s, the echo will be heard; if the time interval is less than \(\frac{1}{10}\) s, reverberation will be heard.
Echo Formula And Examples Class 11 Physics
Practical Applications Of Echo:
1. Measurement Of A Distance: The distance of a distant hill or of any extended reflector can be determined with the help of an echo. In this case, a sharp inarticulate sound, like the sound of a gunshot, is produced, and simultaneously a stopwatch is Started. The stopwatch is stopped just on hearing the echo from the distant reflector.
Let the distance of the reflector from the place of the experiment be D, the time interval between the original sound and the echo heard be t, and the velocity of sound In air be V.
∴ Distance traveled by sound = Vt
Since sound travels the distance D and again returns to the place of experiment, the total distance traveled Is 2D.
∴ 2D = Vt or, D = \(\frac{Vt}{2}\)
Knowing the velocity of sound in air (V) and the time (t) from the stopwatch, the distance (D) of the reflector can be determined.
Echo In Wave Motion Class 11
2. Measurement Of The Depth Of A Sea: The depth of a sea can be measured with the help of an echo. A source S containing some explosive material is kept at a depth h from one end of a ship and a hydrophone H (an underwater microphone) is kept immersed at the same depth h from the other end. A loud sound is produced due to the explosion at S. Sound can reach the hydrophone along two paths
- Straight line path sh and
- Path soh after reflection from the bottom O of the sea.
The sound that reaches along SH is called original sound and the sound that reaches along SOH is called reflected sound. The hydrophone electrically records the time intervals in which sound travels along the direct path SH, as well as along the reflected path SOH.
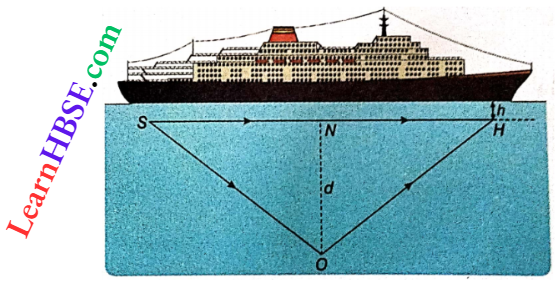
Let the velocity of sound in water be V, the depth of the source and the hydrophone from the surface of the sea be h, the depth of the sea with respect to the source or the hydrophone be NO = d, time taken by the sound to reach the hydrophone directly be t1, and time taken by the echo be t2.
According to the figure, SH = \(V t_1 \text {, i.e., } S N=\frac{V t_1}{2}\)
Again, SO + OH = Vt2
or, \(S O=\frac{V t_2}{2}\) [because SO=OH]
∴ d = ON = \(\sqrt{S O^2-S N^2}=\sqrt{\left(\frac{V t_2}{2}\right)^2-\left(\frac{V t_1}{2}\right)^2}\)
= \(\frac{V}{2} \sqrt{t_2^2-t_1^2}\)
So, the depth of the sea from its surface is,
D = h + d = \(h+\frac{V}{2} \sqrt{t_2^2-t_1^2}\) .
So if V is known, the depth D of the sea can be determined.
If the depth of the sea is very large, the length of the path SH is very small compared to the path SOH. So, t1 may be neglected relative to t2, and h may be neglected relative to d,
i.e., in that case, D = \(\frac{V t_2}{2}.\)
This method is called echo depth ranging or SONAR (Sound Navigation And Ranging).
Conditions For Echo Class 11 Physics
3. Measurement Of The Altitude Of An Airplane: The altitude of a flying airplane can also be measured with the help of an echo. Let us consider an airplane flying horizontally at a height h along the path AB with a velocity v as shown.
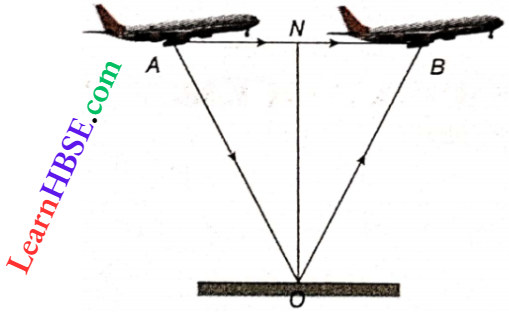
When the plane is at A, a loud sound is produced and the echo is heard after time t when the plane is at B. So, sound reflects from the ground at point O and reaches the airplane along the path AOB, where AO = OB.
Let the velocity of the plane be v, the velocity of sound in air be V, and the time interval between the original sound and the echo be t.
∴ Distance traveled by the plane = AB = vt
i.e., AN = \(\frac{v t}{2}\) [AN = NB]
Again, the distance travelled by the sound is AO + OB = Vt
i.e., AO = \(\frac{v t}{2}\) [AO = OB]
So, the altitude of the plane,
h = \(O N=\sqrt{A O^2-A V^2}=\sqrt{\left(\frac{V t}{2}\right)^2-\left(\frac{v t}{2}\right)^2}=\frac{t}{2} \sqrt{V^2-v^2}\)
Therefore, knowing v, V, and t, the altitude h of the plane can be determined from the above equation.
Class 11 Physics Unit 10 Oscillation And Waves Chapter 3 Wave Motion Echo Numerical Examples
Example 1. A shell is fired from a motor boat moving along the I surface of a sea with a speed of 60 km · h-1 towards j the shore. The echo of the firing is heard in the motor, boat after 9s. What was the distance of the boat from the shore at the time of firing? The velocity of sound = 330 m · s-1.
Solution:
Given
A shell is fired from a motor boat moving along the I surface of a sea with a speed of 60 km · h-1 towards j the shore. The echo of the firing is heard in the motor, boat after 9s.
Distance travelled by sound in 9 s = 330 x 9 = 2970 m
Now, \(60 \mathrm{~km} \cdot \mathrm{h}^{-1}=\frac{60 \times 1000}{60 \times 60} \mathrm{~m} \cdot \mathrm{s}^{-1}=\frac{50}{3} \mathrm{~m} \cdot \mathrm{s}^{-1}\)
So, the distance traveled by the motor boat in 9 s is, = \(\frac{50}{3}\) x 9 = 150 m
If the distance of the shore at the time of firing is xm, then the sound of firing moves x m and then returns (x-150) m after reflection from the shore.
So, x+(x- 150) =2970
or, 2x = 2970 + 150 or, 2x = 3120 or, x = 1560
So, the distance of the motor boat from the shore at the time of firing is 1560 m or 1.56 km.
Derivation Of Echo Formula Class 11
Example 2. What should be the minimum distance of a reflector to hear the echo of a tetrasyllable word? Velocity of sound= 330 m · s-1.
Solution:
The minimum time interval required between the original sound and the echo of a tetrasyllabic word = 4 x \(\frac{1}{5}\) = \(\frac{4}{5}\)s.
∴ Minimum required distance = \(\frac{330 \times 4 / 5}{2}=132 \mathrm{~m}\)
Velocity Of Sound And Echo Class 11 Physics
Example 3. A man Is approaching a hill with a velocity of 5 m · s-1. He fires a gun when he is 3 km away from the hill. When and where will he listen to the echo? The velocity of sound = 355 m · s-1.
Solution:
Given
A man Is approaching a hill with a velocity of 5 m · s-1. He fires a gun when he is 3 km away from the hill.
3km = 3000m
Let us consider that the man advances x m after firing the gim and before hearing the echo.
Time required for this purpose, t = \(\frac{x}{5}\) s
Distance travelled by sound in that time = 3000 +(3000-x) = (6000 -x) m
∴ t = \(\frac{6000-x}{355} \mathrm{~s}\)
i.e., \(\frac{x}{5}=\frac{6000-x}{355} \text { or, } 360 x=5 \times 6000\)
or, \(x=\frac{5 \times 6000}{360}=\frac{250}{3}=83.3 \mathrm{~m}\)
∴ t = \(\frac{x}{5}=\frac{83.3}{5}=16.67 \mathrm{~s}\)
So, the man will listen to the echo after traveling 835 m, 16.67s after firing the gun.
Wave Motion And Its Types Class 11
Example 4. A gun is fired from an airplane moving horizontally with a velocity of 180 km h and the echo of the sound after reflection from the ground Is heard after 3s. What is the height of the airplane? The velocity of sound = 340 m · s-1.
Solution:
Given
A gun is fired from an airplane moving horizontally with a velocity of 180 km h and the echo of the sound after reflection from the ground Is heard after 3s.
180 \(\mathrm{~km} \cdot \mathrm{h}^{-1}=\frac{180 \times 1000}{60 \times 60} \mathrm{~m} \cdot \mathrm{s}^{-1}=50 \mathrm{~m} \cdot \mathrm{s}^{-1}\)
Distance travelled by the plane in 3 s = AB = 50 x 3 m
So, \(A N=\frac{A B}{2}=\frac{50 \times 3}{2}=25 \times 3 \mathrm{~m}\)
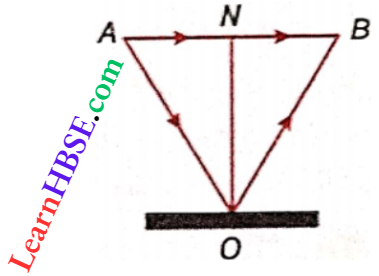
Distance travelled by sound in that time = AO + OB =340 x3 m
i.e AO = \(\frac{340 \times 3}{2}=170 \times 3 \mathrm{~m}\)
So, height of the plane = ON = \(\sqrt{A O^2-A N^2}\)
= \(\sqrt{(170 \times 3)^2-(25 \times 3)^2}\)
= \(\sqrt{(510)^2-(75)^2} \approx 504.45 \mathrm{~m}\)
Numerical Problems On Echo Class 11 Physics
Example 5. A man standing 85 m away from a high wall is clapping in a regulated manner. When he claps twice per second, each clap coincides with the echo of its previous clap. Determining the velocity of sound in air.
Solution:
Given
A man standing 85 m away from a high wall is clapping in a regulated manner. When he claps twice per second, each clap coincides with the echo of its previous clap.
Time interval between two claps, t = \(\frac{1}{2}\) s
If V is the velocity of sound in air, 2s = Vt
∴ 2 x 85 = \(V \times \frac{1}{2} \quad \text { or, } V=85 \times 4=340 \mathrm{~m} \cdot \mathrm{s}^{-1} \text {. }\)
Example 6. A ship’s sound measuring experiment sends our pulses looking for echoes from submarines within a 3 km radius. What should be the pulse repetition frequency? Given, the velocity of sound in water = 1500 m · s-1
Solution:
Given
A ship’s sound measuring experiment sends our pulses looking for echoes from submarines within a 3 km radius.
Total path travelled by the pulses = 3 + 3 = 6km = 6000m
Time taken by a pulse for the to and fro journey is,
t = \(\frac{6000}{1500}=4 \mathrm{~s}\)
∴ Pulse repetition frequency,
n = \(\frac{1}{4}\) per second = 15 per minute.
The pulse repetition frequency = 15 per minute.
Wave Motion Class 11 NCERT Solutions
Example 7. A man standing at a certain distance from a bill is heating a drum. He observes that if he beats the drum at the rate of 40 min-1, the echo is not heard distinctly. He advances 90 m towards the hill and observes that If he beats the drum at the rate of 60 min-1, the echo cannot be heard distinctly. Determine the distance of the first position of the man from the hill and aldo the velocity of sound.
Solution:
Given
A man standing at a certain distance from a bill is heating a drum. He observes that if he beats the drum at the rate of 40 min-1, the echo is not heard distinctly. He advances 90 m towards the hill and observes that If he beats the drum at the rate of 60 min-1, the echo cannot be heard distinctly.
Let the distance of the first position of the man from the hill be x and velocity of sound be V.
In the first case, the time interval between two consecutive sounds, \(t_1=\frac{60}{40}=\frac{3}{2} \mathrm{~s}\)
∴ When echo is just not heard distinctly, 2x = V x \(\frac{3}{2}\) s …(1)
In the second case, the time interval between two consecutive sounds, \(t_2=\frac{60}{60}\) = 1s
∴ In this case, when the echo is just not heard distinctly, 2(x-90) = V x 1 ……(2)
Dividing {2} by (1) we have, \(\frac{2(x-90)}{2 x}=\frac{V \times 2}{V \times 3} \quad \text { or, } 3 x-270=2 x \quad \text { or, } x=270 \mathrm{~m}\)
From equation (1) we have,
2 x 270 = \(V \times \frac{3}{2} \quad \text { or, } V=360 \mathrm{~m} \cdot \mathrm{s}^{-1} \text {. }\)
