Class 11 Physics Superposition Of Waves Question and Answers

Superposition Of Waves Shorts Answer Type Questions

Question 1. The resultant displacement due to the superposition of two identical progressive waves is y = 5cos(0.2πx)sin(64πt), where x, y are in cm and t is in sec. Find the equations of the two superposing waves.
Answer:

Given

Resultant displacement due to the superposition of two identical progressive waves,

∴ y = \(5 \cos (0.2 \pi x) \sin (64 \pi t)\)

= \(\frac{5}{2} \times 2 \cos (0.2 \pi x) \sin (64 \pi t)\)

= \(\frac{5}{2}[\sin (64 \pi t+0.2 \pi x)+\sin (64 \pi t-0.2 \pi x)]\)

So, the expression of those progressive waves is as follows,

∴ \(y_1=2.5 \sin (64 \pi t+0.2 \pi x)\)

and \(y_2=2.5 \sin (64 \pi t-0.2 \pi x)\)

Superposition Of Waves Class 11 Notes

Question 2. The expression for a standing wave is y(x, t) = 2sin(0.1πx)cos100πt, where x,y are in cm and t is in second. Find the distance between a node and the next antinode of the wave.
Answer:

Given

The expression for a standing wave is y(x, t) = 2sin(0.1πx)cos100πt, where x,y are in cm and t is in second.

y(x, t) = 2sin(0.1 π x)cos100πt = asinkxcotωt

Here, k = 0.1π, ω = 100π

So, \(\lambda=\frac{2 \pi}{k}=\frac{2 \pi}{0.1 \pi}=20 \mathrm{~cm}\)

So, the separation between a node and the next antinode

= \(\frac{\lambda}{4}\) = 5 cm

Question 3. Does the principle of conservation of energy always hold in the case of the superposition of two sound waves?
Answer: No, do not hold always.

Question 4.

1. Two waves are expressed as, \(y_1=a \sin \omega_1\left(\frac{x}{c}-t\right) \text { and } y_2=a \sin \omega_2\left(\frac{x}{c}-t\right)\) Find the resultant displacement due to superposition of the two waves.
2. Determine the amplitude of the resultant displace¬ment at x = 0.
3. If the two frequencies are nearly equal, find the beat frequency.

Answer:

1. Two waves are expressed as, \(y_1=a \sin \omega_1\left(\frac{x}{c}-t\right) \text { and } y_2=a \sin \omega_2\left(\frac{x}{c}-t\right)\)

So, the resultant displacement due to the superposition of these two waves is,

y = \(y_1+y_2=a \sin \omega_1\left(\frac{x}{c}-t\right)+a \sin \omega_2\left(\frac{x}{c}-t\right)\)

= \(2 a \sin \left[\frac{\left(\omega_1+\omega_2\right) \frac{x}{c}-\left(\omega_1+\omega_2\right) t}{2}\right]\)

x \(\cos \left[\frac{\left(\omega_1-\omega_2\right) \frac{x}{c}-\left(\omega_1-\omega_2\right) t}{2}\right]\)

= \(2 a \sin \left[\frac{\left(\omega_1+\omega_2\right) x}{2 c}-\frac{\left(\omega_1+\omega_2\right) t}{2}\right]\)

x \(\cos \left[\frac{\left(\omega_1-\omega_2\right) x}{2 c}-\frac{\left(\omega_1-\omega_2\right) t}{2}\right]\)

So, \(y=A \sin \left[\frac{\left(\omega_1+\omega_2\right) x}{2 c}-\frac{\left(\omega_1+\omega_2\right) t}{2}\right]\)

where, A = \(2 a \cos \left[\frac{\left(\omega_1-\omega_2\right) x}{2 c}-\frac{\left(\omega_1-\omega_2\right) t}{2}\right]\)

2. Amplitude of resultant displacement at x = 0

A = \(2 a \cos \left[-\frac{\left(\omega_1-\omega_2\right) t}{2}\right]=2 a \cos \frac{\left(\omega_1-\omega_2\right) t}{2}\)

3. Let ω₁ = 2πn₁ and ω₂ = 2πn₂, where n₁ and n₂ are two nearly equal frequencies.

∴ \(n_1=\frac{\omega_1}{2 \pi} \text { and } n_2=\frac{\omega_2}{2 \pi}\)

So, beat frequency

= \(n_1 \sim n_2=\frac{\omega_1}{2 \pi} \sim \frac{\omega_2}{2 \pi}=\frac{1}{2 \pi}\left(\omega_1 \sim \omega_2\right)\)

Numerical Problems On Superposition Of Waves Class 11

Question 5. When the waves y₁ = Asinωt and y₂ = A cosωt are superposed, then the resultant amplitude will be

1. √2A
2. \(\frac{1}{\sqrt{2}} A\)
3. A
4. 2A

Answer:

Resultant wave,

y = \(y_1+y_2=A \sin \omega t+A \cos \omega t\)

= \(\sqrt{2} A\left(\sin \omega t \cdot \frac{1}{\sqrt{2}}+\cos \omega t \cdot \frac{1}{\sqrt{2}}\right)\)

= \(\sqrt{2} A\left(\sin \omega t \cos \frac{\pi}{4}+\cos \omega t \sin \frac{\pi}{4}\right)\)

= \(\sqrt{2} A \sin \left(\omega t+\frac{\pi}{4}\right)\)
\end{aligned}

Hence, resultant amplitude = √2A.

The option 1 is correct.

Question 6. A tuning fork produces 10 beats per second with a sonometer wire of length 93cm and 100 cm. Find the frequency of the fork.
Answer:

Given

A tuning fork produces 10 beats per second with a sonometer wire of length 93cm and 100 cm.

Frequency of the fundamental tone of the sonometer wire, n = \(\frac{1}{2 I} \sqrt{\frac{T}{m}}\), then

∴ \(\frac{n_1}{n_2}=\frac{100}{95}=\frac{20}{19} \text { [here, } n_1>n_2 \text { ] }\)

If the frequency of the tuning fork is x, for 10 beats per second, n – x = 10 and  x – n = 0

Adding them, we get n₁ – n₂ = 20

So, \(\frac{n_1}{n_2}-1=\frac{20}{n_2}\)

or, \(\frac{20}{19}-1=\frac{20}{n_2}\)

or, \(\frac{1}{19}=\frac{20}{n_2} or, \quad n_2=380 \mathrm{~Hz}\)

Now, \(x-m_2=10\)

∴ x = \(10 \div n_2=10+380=390 \mathrm{~Hz}\)

Superposition Of Waves Class 11 NCERT Solutions

Question 7. If the tension and diameter of a sonometer wire of fundamental frequency n are doubled and the density halved, then its fundamental frequency will become

1. \(\frac{n}{4}\)
2. \(\sqrt{2} n\)
3. n
4. \(\frac{n}{\sqrt{2}}\)

Answer:

Mass per unit length of a wire m = πr²ρ [r = radius, ρ = density of the material

∴ Fundamental frequency, n = \(\frac{1}{2 l} \sqrt{\frac{T}{m}}=\frac{1}{2 l r} \sqrt{\frac{T}{\pi \rho}}\)

∴ In this case, after changing the tension and density of the sonometer wire, the frequency is

n’ = \(\frac{1}{2 l(2 r)} \sqrt{\frac{2 T}{\pi\left(\frac{\rho}{2}\right)}}=\frac{1}{4 l r} \sqrt{\frac{4 T}{\pi \rho}}\)

= \(\frac{1}{2 l r} \sqrt{\frac{T}{\pi \rho}}=n\)

[If diameter is doubled radius is also doubled]

∴ Fundamental frequency remains the same.

The option 3 is correct.

Question 8. How much is the separation between two consecutive nodes in a stationary wave?
Answer:

If the length of the stationary wave is T, then the distance between two consecutive nodes is = \(\frac{\lambda}{2}\).

Wave Interference And Superposition Class 11

Question 9. Two traveling waves superpose to form a stationary wave whose equation is y(x, t) = 5sin(0.1πx)cos50πt, where x, y are in cm and f is in s. Find the equations of the two superposing traveling waves.
Answer:

Given

Two traveling waves superpose to form a stationary wave whose equation is y(x, t) = 5sin(0.1πx)cos50πt, where x, y are in cm and f is in s.

y(x, t) = 5sin(0.1πx)cos50πt

= \(\frac{5}{2}\) x 2sin(0.1πx)cos50πt

= \(\frac{5}{2}\) x [sin(0.1πx + 50πt) + sin(0.1πx -50πt)]

∴ The equations of the two traveling waves are, \(y_1=\frac{5}{2} \sin (0.1 \pi x+50 \pi t)\)

and \(y_2=\frac{5}{2} \sin (0.1 \pi x-50 \pi t)\)

Question 10. Two tuning forks vibrating simultaneously produce 5 beats per second. The frequency of one fork is 275 Hz. A small wax is attached to the other fork and 2 beats per second are produced when the two vibrate simultaneously. Find the frequency of the other fork.
Answer:

Given

Two tuning forks vibrating simultaneously produce 5 beats per second. The frequency of one fork is 275 Hz. A small wax is attached to the other fork and 2 beats per second are produced when the two vibrate simultaneously.

Let the frequency of the other fork be x, beat frequency = difference in the frequencies of the two tuning forks.

If x < 275 Hz, before waxing we have, 275 -x = 5 or x – 270 Hz. After waxing, x will decrease, so the beat frequency will increase.

∴ x > 275 Hz and before waxing we have, x – 275 = 5 or x – 280 Hz . After waxing, x will decrease slightly, so the beat frequency will decrease to 2.

Question 11. Displacement of a particle, in periodic motion, is represented by y = \(4 \cos ^2\left(\frac{1}{2}\right) \sin (1000 t)\). If the equation is the superposition of n number of simple harmonic motion then n becomes

1. 1
2. 2
3. 3
4. 4

Answer:

The option 3 is correct.

Question 12. A whistle whose air column is open at both ends has a fundamental frequency of 5100 Hz. If the speed of sound in air is 340 m · s^-1, the length of the whistle in cm is

1. 5/3
2. 10/3
3. 5
4. 20/3

Answer:

If the length of the whistle is l, then the frequency of the fundamental tone, n₀ = \(\frac{V}{2}\)[V = velocity of sound ]

∴ l = \(\frac{V}{2 n_0}=\frac{340}{2 \times 5100}=\frac{1}{30} \mathrm{~m}=\frac{10}{3} \mathrm{~cm}\)

The option 2 is correct.

Constructive And Destructive Interference Class 11

Question 13. Sound waves are passing through two routes one in a straight path and the other along a semicircular path of radius r and are again combined into one pipe and superposed as shown. If the velocity of sound waves in the pipe is v, then frequencies of resultant waves of maximum amplitude will be integral multiples of

1. \(\frac{v}{r(\pi-2)}\)
2. \(\frac{v}{r(\pi-1)}\)
3. \(\frac{2 v}{r(\pi-1)}\)
4. \(\frac{v}{r(\pi+1)}\)

Answer:

Path difference = πr – 2 r = (π-2)r

According to the question, (π – 2)r = pλ, where p = any +ve integer

If the frequency is n, V = nλ or, \(n=\frac{V}{\lambda}=\left[\frac{V}{(\pi-2) r}\right] p\)

The option 1 is correct.

Question 14. The length of an open organ pipe is twice the length of another closed organ pipe. The fundamental frequency of the open pipe is 100Hz. The frequency of the third harmonic of the closed pipe is

1. 100Hz
2. 200Hz
3. 300Hz
4. 150Hz

Answer:

Frequency of the fundamental tone of the open organ pipe

= \(\frac{v}{2 l}\) [v = velocity of sound, l = length of the pipe]

∴ \(\frac{v}{2 l}\) = 100

Length of the closed organ pipe, L =  \(\frac{l}{2}\)

In this pipe, the second harmonic will be absent.

Frequency of the third harmonic

= 3 times the frequency of the fundamental tone

= \(3 \cdot \frac{v}{4 L}=3 \cdot \frac{v}{2 l}=3 \times 100=200 \mathrm{~Hz}\)

The option 3 is correct.

Superposition Of Waves Formula Class 11

Question 15. A uniform string of length L and mass M is fixed at both ends while it is subject to a tension T. It can vibrate at frequencies (v) given by the formula (where n = 1, 2m 3, ….)

1. \(\nu=\frac{n}{2} \sqrt{\frac{T}{M L}}\)
2. \(\nu=\frac{n}{2 L} \sqrt{\frac{T}{M}}\)
3. \(\nu=\frac{1}{2 n} \sqrt{\frac{T}{M L}}\)
4. \(\nu=\frac{n}{2} \sqrt{\frac{T L}{M}}\)

Answer:

The frequency of nth harmonic, emitted due to vibration of a stretched string, \(\nu=\frac{n}{2 L} \sqrt{\frac{T}{m}}\) where m = \(\frac{M}{L}\)

= \(\frac{n}{2 L} \sqrt{\frac{T L}{M}}=\frac{n}{2} \sqrt{\frac{T}{M L}}\)

The option 1 is correct.

Question 16. A pipe of length 85 cm is closed from one end. Find the number of possible natural oscillations of the air column in the pipe whose frequencies lie below 1250 Hz. The velocity of sound in air is 340 m/s.

1. 12
2. 8
3. 6
4. 4

Answer:

Fundamental frequency = \(\frac{V}{4 l}=\frac{34000}{4 \times 85}=100 \mathrm{~Hz}\)

So, possible frequencies below 1250 Hz are 100, 300, 500, 700, 900 and 1100 Hz.

The option 3 is correct.

Question 17. When a string is divided into three segments of length l₁, l_2, and l₃ the fundamental frequencies of these three segments are ν₁, ν₂, and ν₃ respectively. The original fundamental frequency (ν) of the string is

1. \(\sqrt{\nu}=\sqrt{\nu_1}+\sqrt{\nu_2}+\sqrt{\nu_3}\)
2. \(\nu=\nu_1+\nu_2+\nu_3\)
3. \(\frac{1}{\nu}=\frac{1}{\nu_1}+\frac{1}{\nu_2}+\frac{1}{\nu_3}\)
4. \(\frac{1}{\sqrt{\nu}}=\frac{1}{\sqrt{\nu_1}}+\frac{1}{\sqrt{\nu_2}}+\frac{1}{\sqrt{\nu_3}}\)

Answer:

Let l be the length of the string.

Fundamental frequency is given by \(\nu=\frac{1}{2 l} \sqrt{\frac{T}{\mu}}\)

or, \(\nu \propto \frac{1}{l}\) [because T and \(\mu\) are constant] or, \(\nu=\frac{k}{l}\), where k is a constant

Here, \(l_1=\frac{k}{\nu_1}, l_2=\frac{k}{\nu_2}, l_3=\frac{k}{\nu_3} and l=\frac{k}{\nu}\)

∴ \(\frac{1}{\nu}=\frac{1}{\nu_1}+\frac{1}{\nu_2}+\frac{1}{\nu_3} \quad\left[because l=l_1+l_2+l_3\right]\)

The option 3 is correct

Superposition Of Waves Examples Class 11

Question 18. The number of possible natural oscillations of the air column in a pipe closed at one end of length 85 cm whose frequencies lie below 1250 Hz are (velocity of sound = 350 m · s^-1).

1. 4
2. 5
3. 7
4. 6

Answer:

Velocity of sound (V) = 340 m · s¹ = 34000 cm · s¹

Length of dosed pipe (l) = 85 cm

So, fundamental frequency, \(n_0=\frac{V}{4 l}=\frac{34000}{4 \times 85}=100 \mathrm{~Hz}\)

Thus, present natural frequencies are odd multiples of the fundamental frequency, i.e., 100,300,500,700,900,1100

So, number of natural oscillations = 6

The option 4 is correct.

Question 19. The fundamental frequency of a closed organ pipe of length 20 cm is equal to the second overtone of an organ pipe open at both ends. The length of the organ pipe open at both ends is

1. 80cm
2. 100cm
3. 120cm
4. 140cm

Answer:

Frequency of the fundamental tone of the closed organ pipe

= \(\frac{\nu}{4 l}=\frac{\nu}{4 \times 20}=\frac{\nu}{80}\)[v = velocity of sound]

If L is the length of the organ pipe open at both ends, frequency of the fundamental tone = \(\frac{v}{2 L}\) then the frequency of the second overtone, i.e., the third harmonic, = \(\left(3 \cdot \frac{v}{2 L}\right)\)

According to the question, \(\frac{v}{80}=3 \cdot \frac{v}{2 L} \text { or, } L=\frac{3}{2} \times 80=120 \mathrm{~cm}\)

The option 3 is correct.

Question 20. An air column, closed at one end and open at the other, resonates with a tuning fork when the smallest length of the column is 50 cm. The next larger length of the column resonating with the same tuning fork is

1. 100 cm
2. 150 cm
3. 200 cm
4. 66.7 cm

Answer:

For 1st resonance, the length of the air column is l₁ = 50 cm

Let, for 2nd resonance the length of the air column is l₂

Resonant frequency for 1st resonance n = \(\frac{V}{4 l_1}\)

Resonant frequency for 2nd resonance n = \(\frac{3V}{4 l_2}\)

∴ \(l_1=\frac{V}{4 n} \text { and } l_2=\frac{3 V}{4 n}\)

∴ \(l_1=\frac{l_2}{3} \quad \text { or, } l_2=3 l_1=3 \times 50=150 \mathrm{~cm}\)

The option 2 is correct.

Applications Of Superposition Of Waves Class 11

Question 21. Two open organ pipes of fundamental frequencies n₁ and n₂ are joined in series. The fundamental frequency of the new pipe so obtained will be:

1. \(\left(n_1+n_2\right)\)
2. \(\frac{n_1+n_2}{2}\)
3. \(\sqrt{n_1^2+n_2^2}\)
4. \(\frac{n_1 n_2}{n_1+n_2}\)

Answer:

⇒ \(n_1=\frac{V}{2 l_1},\)

∴ \(l_1=\frac{V}{2 n_1} ; \text { similarly } l_2=\frac{V}{2 n_2}\)

∴ \(l_1+l_2=\frac{V}{2}\left(\frac{1}{n_1}+\frac{1}{n_2}\right)=\frac{V\left(n_1+n_2\right)}{2 n_1 n_2}\)

Fundamental frequency in joined open pipe

n = \(\frac{V}{2\left(l_1+L_2\right)}=\frac{V}{2} \cdot \frac{2 n_1 n_2}{V\left(n_1+n_2\right)}=\frac{n_1 n_2}{n_1+n_2}\)

The option 4 is correct.

Question 22. The fundamental frequency in an open organ pipe is equal to the third harmonic of a closed organ pipe. If the length of the closed organ pipe is 20 cm, the length of the open organ pipe is

1. 12.5 cm
2. 8 cm
3. 13.2 cm
4. 16 cm

Answer:

Third harmonic of a closed organ pipe, \(n_2=\frac{3 V}{4 l}\)

[l = length of closed organ pipe, V = velocity of sound]

Fundamental frequency of open organ pipe,

∴ \(\frac{3 V}{4 l}=\frac{V}{2 l^{\prime}} \quad \text { or, } l^{\prime}=\frac{4 l}{3 \times 2}=\frac{2 l}{3}=\frac{2 \times 20}{3}\)

or, l’ = 13.33 cm

The option 3 is correct.

Question 23. A tuning fork is used to produce resonance in a glass tube. The tire length of the air column in this tube can be adjusted by a variable piston. At room temperature of 27°C two successive resonances are produced at 20 cm and 73 cut of column length. If the frequency of the tuning fork is 320 Hz, the velocity of sound in air at 27°C is

1. 350 m/s
2. 339 m/s
3. 330 m/s
4. 300 m/s

Answer:

(2n-1)\(\frac{\lambda}{4}\) = 20…(1)

(2n+1)\(\frac{\lambda}{4}\) = 73…(2)

Subtracting equation (2) from equation (1), we get \((2 n+1-2 n+1) \frac{\lambda}{4}=(73-20)\)

or, \(\frac{\lambda}{2}=53 or, \lambda=106 \mathrm{~cm}=\frac{106}{100} \mathrm{~m}\)

∴ V = \(n \lambda=320 \times \frac{106}{100}=339.2 \mathrm{~m} / \mathrm{s}\)

The option 2 is correct.

Superposition Of Waves Derivation Class 11

Question 24. A progressive wave is given by y(x, t) = 8cos(300t-0.15x) where x in m, y in cm, and t in second. What is the

1. The direction of propagation,
2. Wavelength,
3. Frequency,
4. Wave speed and
5. The phase difference between two points 0.2 m apart?

Answer:

y(x,t)= 8 cos (300t- 0.15.x)

Comparing this equation with the stationary wave equation

y = \(a \cos 2 \pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)\), we have,

1. The direction of propagation is +x-axis
2. \(\frac{2 \pi}{\lambda}=0.15 \quad or, \lambda=\frac{2 \pi}{0.15}=41.87 \mathrm{~m}\)
3. \(\frac{2 \pi}{T}=300\) or, \(2 \pi n=300\) or, \(n=\frac{300}{2 \pi}=47.78 \mathrm{~Hz}\)
4. v = \(\lambda n=\frac{2 \pi}{0.15} \times \frac{300}{2 \pi}=2000 \mathrm{~m} / \mathrm{s}\)
5. \(\phi=\frac{2 \pi}{\lambda} \Delta x=\frac{2 \pi}{\lambda} \times 0.2\)

= \(\frac{2 \pi \times 0.2 \times 0.15}{2 \pi}=0.03 \mathrm{rad}\)

Question 25. A stationary wave is y = 12sin300tcos2x. What is the distance between the two nearest nodes?
Answer:

Given, y = 12sin300tcos2x.

Comparing this equation with the stationary wave equation, y = 2Asinωtcoskx we have, k = 2.

So, the distance between two consecutive nodes = \(\frac{\lambda}{2}\) where λ is the wavelength.

So, \(k=\frac{2 \pi}{\lambda} \quad$ or, $\frac{2 \pi}{\lambda}=2\) or, \(\frac{\pi}{(\lambda / 2)}=2\)

∴ \(\frac{\lambda}{2}=\frac{\pi}{2}\)

So the distance between two nearest nodes is \(\frac{\pi}{2}\)

Principle Of Superposition Of Waves Class 11

Question 26. In an open organ pipe, the third harmonic is 450 Hz. What is the frequency of the fifth harmonic?
Answer:

For the third harmonic frequency in an open organ pipe, n₃ = 3n₀

Here, n₃ = 450 Hz

∴ 450 = 3n₀ or, n₀ = 150 Hz

For fifth harmonic, n₅ = 5 n₀

Now, n₀ = 150 Hz

∴ n₅ = 5 x 150 Hz or, n₅ = 750 Hz

Question 27. The frequencies of the two tuning forks A and B are 250 Hz and 255 Hz respectively. Both are sounded together. How many beats will be heard in 5 seconds?
Answer:

Given frequencies are f₁ = 250 Hz; f₂ = 255 Hz.

Hence, the number of beats per second or beat frequency = (255-250) = 5.

So the number of beats heard in 5 seconds = 5×5 = 25.

Question 27. An incident wave and a reflected wave are represented by \(\xi_1=a \sin \frac{2 \pi}{\lambda}(\nu t-x) \text { and } \xi_2=a \sin \frac{2 \pi}{\lambda}(\nu t+x)\) Derive the equation of the stationary wave and calculate the position of the nodes and antinodes.
Answer:

Given

An incident wave and a reflected wave are represented by \(\xi_1=a \sin \frac{2 \pi}{\lambda}(\nu t-x) \text { and } \xi_2=a \sin \frac{2 \pi}{\lambda}(\nu t+x)\)

According to the principle of superposition

⇒ \(\xi =\xi_1+\xi_2=a \sin \frac{2 \pi}{\lambda}(\nu t-x)+a \sin \frac{2 \pi}{\lambda}(\nu t+x)\)

= \(2 a \cos \frac{2 \pi x}{\lambda} \sin \frac{2 \pi}{\lambda} \nu t\)

= \(2 a \cos \frac{2 \pi}{\lambda} x \sin 2 \pi n t[because v=n \lambda]\)

= \(A \sin 2 \pi n t, \text { where amplitude, } A=2 a \cos \frac{2 \pi}{\lambda} x\)

This equation represents a stationary wave.

For nodes, \(\xi\) = 0 for all values of t, i.e„ \(\cos \frac{2 \pi}{\lambda} x=0\) [because A=0]

or, \(\cos \frac{2 \pi x}{\lambda}=\cos (2 n+1) \frac{\pi}{2}, n=0,1,2 \cdots\)

or, x = \((2n+1) \frac{\lambda}{4}\)

The position of nodes at which particles do not vibrate, are x = \(\frac{\lambda}{4}, \frac{3 \lambda}{4}, \frac{5 \lambda}{4}\) etc.

Distance between two successive nodes = \(\frac{\lambda}{2}\).

For antinodes, \(\cos \frac{2 \pi}{\lambda}= \pm 1\), so that the particles vibrate with maximum amplitude ±2a. Hence, antinodes occur at a position for which

∴ \(\cos \frac{2 \pi x}{\lambda}=\cos n \pi, n=0,1,2 \cdots\)

or, \(\frac{2 \pi x}{\lambda}=n \pi\) or, \(x=\frac{n \lambda}{2}\)

So, the position of antinodes are x = \(0, \frac{\lambda}{2}, \lambda, \frac{3 \lambda}{2} \text { etc. }\)

The distance between two antinodes = \(\frac{\lambda}{2}.\)

Question 28. If an open organ pipe of length 20 cm resonates with 1 kHz, in the third harmonic mode, find the wavelength of the standing wave produced.
Answer:

Given

If an open organ pipe of length 20 cm resonates with 1 kHz, in the third harmonic mode,

Let l = length of an open organ pipe. For the fundamental mode of vibration, as shown, the wavelengths λ is such that, l = \(\frac{\lambda}{2}.\) or, λ = 21

Now, V = nλ, or, nλ = constant, as the velocity of sound is constant.

∴ \(\frac{1}{n}\)

An open organ pipe produces all the overtones. So the frequency of the 3rd harmonic would be three times that of the fundamental. Then the wavelength would be one-third. For the fundamental. We already have, λ = 2l.

So, for the 3rd harmonic, wavelength = \(\frac{2 l}{3}=\frac{2 \times 20}{3}=13.3 \mathrm{~cm}\)

[From the resonance condition, frequency = 1000 Hz.

∴ V = nλ = 1000 x 13.3 = 13300 cm · s^-1 = 133 m · s^-1

This is not the correct value of V, it should be 330 m · s^-1; incorrect data has been given.]

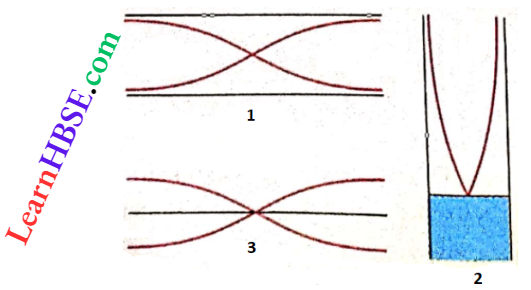
Question 29. Draw the stationary wave pattern in the fundamental mode for the following cases:

1. An open organ pipe
2. Resonance column apparatus
3. A rigid metallic rod clamped in the middle, the rod is hit with a stick at one of its free ends.

Answer:

1. Two antinodes at the two open ends and a node between them.
2. An antinode at the open end and the nearest node at the top of the liquid surface.
3. Two antinodes at the free ends and only one node between them at the clamped midpoint. It is to be noted that sound waves are always longitudinal waves. For convenience only they have been drawn as transverse waves.

Question 30. Two waves of nearly the same frequencies traveling in the same direction superimpose on each other. Name the resulting phenomenon.
Answer: Formation of beats.

Question 31. Calculate the speed of sound in a gas in which two waves of wavelengths 1.00 m and 1.01m produce 4 beats per second.
Answer:

Let V be the velocity of sound.

If λ₁ = 1 m and λ₂ = 1.01 m then

Frequencies \(n_1=\frac{V}{\lambda_1}=\frac{V}{1} \text { and } n_2=\frac{V}{\lambda_2}=\frac{V}{1.01}\)

Since, n₁ > n₂

So, n₁ – n₂ = 4

∴ \(\frac{V}{1}-\frac{V}{1.01}=4 \quad \text { or, } V \times \frac{1.01-1}{1.01}=4 \)

or, V = \(\frac{1.01 \times 4}{0.01}=404 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Question 32. A transverse harmonic wave on a string is described by Y(x, t) =3sin(36t+0.018x+\(\frac{\pi}{4}\)). Where X and Y are in cm and t in sec. The positive direction of x is from left to right.

1. What is speed of this wave?
2. What is its amplitude?
3. What is its frequency?
4. What is the initial phase at the origin?
5. What is its wavelength?

Answer:

Given, \(Y(x, t)=3 \sin \left(36 t+0.018 x+\frac{\pi}{4}\right)\)

It is comparable to the transverse harmonic wave equation as Y(x, t) =Asin(ωt+ kx+ ø)

Thus, A = 3 cm, w = 36 rad/s, k = 0.018 cm^-1 and = \(\phi=\frac{\pi}{4} \mathrm{rad}\).

Speed of the wave, V = nλ

∴ \(\frac{\omega}{k}=\frac{2 \pi n}{\frac{2 \pi}{\lambda}}=n \lambda\)

V = \(\frac{\omega}{k}=\frac{36}{0.018}=20 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Amplitude, A = 3 cm

Frequency, n = \(\frac{\omega}{2 \pi}\) = 5.73 Hz

Phase at the origin = \(\phi=\frac{\pi}{4} \mathrm{rad} .\)

Wavelength, \(\lambda=\frac{2 \pi}{k}=\frac{2 \pi}{0.018}=3.49 \mathrm{~m}\) = 3.49 m