Class 11 Physics Wave Motion Question and Answers

Wave Motion Short Answer Type Questions

Question 1. The equation y= a(sinkxcosωt- coskxsinωt) represents

1. A progressive wave propagating along the positive x-axis with velocity ω/k
2. A progressive wave propagating along the negative x-axis with velocity ω/k
3. A stationary wave
4. Not a wave motion

Answer:

Here, y = asin(kx-ωt); a progressive wave of ω/k velocity, along +ve x direction.

The option 1 is correct.

Question 2. The wavelength of a traveling wave is 2 m. What is the phase difference between two particles 1 m apart in the path of the wave?
Answer:

Given

The wavelength of a traveling wave is 2 m.

For λ = 2m, the phase changes by 2π.

So, for two points separated by 1 m, phase difference = \(\frac{\pi}{2}\) = π

Wave Motion Class 11 Physics Notes

Question 3. Are sound waves longitudinal or transverse?
Answer:

Sound waves are longitudinal waves.

Question 4. The equation of a traveling wave is y- 20 sin (0.2πx-50πt), where x and y are in cm and t is in second. Find out the

1. Amplitude,
2. Wavelength,
3. Frequency and
4. Velocity of the wave.

Answer:

Equation of progressive wave, y = 20 sin (0.2πx-50πt)

1. Amplitude (a) = 20 cm

2. Here, k = \(0.2 \pi \quad \text { or, } \frac{2 \pi}{\lambda}=0.2 \pi\)

∴ \(\lambda=\frac{2 \pi}{0.2 \pi}=10 \mathrm{~cm}\)

So, wavelength = 10 cm

3. According to given equation, angular velocity (ω) = 50 π;

∴ n = \(\frac{\omega}{2 \pi}=\frac{50 \pi}{2 \pi}=25\)

So, frequency = 25 Hz

4. Velocity (V) =nλ = 25 x 10 = 250 cm · s^-1

Types Of Wave Motion Class 11

Question 5. The percentage change of velocity of sound when temperature increases from 0°C to 20°C is

1. 1.5%
2. 2.5%
3. 1.75%
4. 2%

Answer:

The velocity of sound, c ∝ √T

Here, T₁ = 0 + 273 = 273 K

T₂ = 20 + 273 = 293 K

∴ \(\frac{c_{20}}{c_0}=\sqrt{\frac{293}{273}}=\left(1+\frac{20}{273}\right)^{1 / 2} \approx 1+\frac{1}{2} \cdot \frac{20}{273}=\frac{283}{273}\)

So, percentage change of velocity

= \(\left(\frac{283}{273}-1\right) \times 100=3.66 \%\)

None of the options is correct.

Numerical Problems On Wave Motion Class 11

Question 6. The velocity of sound in oxygen gas at STP is v. What will be the velocity of sound in Helium gas under the same conditions?
Answer:

Given

The velocity of sound in oxygen gas at STP is v.

Velocity of sound, c = \(\sqrt{\frac{\nu R T}{M}}\)

At STP, the molar mass of oxygen, M = 32 g

The molar mass of helium, M’ = 4g

Now as oxygen is a diatomic gas, v = \(\frac{7}{5}\)

Again helium is a monoatomic gas, v’ = \(\frac{5}{3}\)

So, \(\frac{\nu^{\prime}}{\nu}=\sqrt{\frac{\nu^{\prime}}{\nu}} \cdot \sqrt{\frac{M}{M^{\prime}}}=\sqrt{\frac{5}{\frac{5}{5}} \times \frac{32}{4}}=\sqrt{\frac{25}{21} \times 8}=3.086\)

∴ v’ = 3.086 v

Question 7. Two sound waves having a phase difference of 60° have path difference of

1. \(2 \lambda\)
2. \(\frac{\lambda}{6}\)
3. \(\frac{\lambda}{2}\)
4. \(\frac{\lambda}{3}\)

Answer:

Phase difference, \(\phi=\frac{2 \pi}{\lambda}\) x path difference (Δx)

or, \(60^{\circ}=\frac{\pi}{3}=\frac{2 \pi}{\lambda} \Delta x\)

∴ \(\Delta x=\frac{\lambda}{6}\)

The option B is correct.

Wave Motion Class 11 NCERT Solutions

Question 8. A stone is dropped from the top of a well of depth 39.2 m and a sound is heard when it reaches the bottom surface after a time of 2.95 s. Find the velocity of sound in the air. (g = 9.8 m/s²)
Answer:

Given

A stone is dropped from the top of a well of depth 39.2 m and a sound is heard when it reaches the bottom surface after a time of 2.95 s.

Depth of the well, h = 39.2 m

The time taken by the stone to travel a 39.2 m distance is,

t = \(\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 39.2}{9.8}}=2 . \sqrt{2}=2.83 \mathrm{~s}\)

The time taken for sound to travel h distance is, t’ = (2.95 – 2.83) = 0.12 s

∴ The velocity of sound in air, v = \(\frac{h}{t^{\prime}}=\frac{39.2}{0.12}\) = 326.67 m/s

Question 9. The frequency of a particle vibrating In a medium is fHz. How many waves are generated in 5 seconds in the medium?
Answer:

Given

The frequency of a particle vibrating In a medium is fHz.

The number of waves generated in 1 second = f

∴ The number of waves generated in 5 seconds = 5f

Wave Motion Examples Class 11

Question 10. A tuning fork in air vibrates at 30 Hz with 5 cm amplitude. If the velocity of sound in air is 330 m · s^-1, derive the expression for the generated traveling wave.
Answer:

Given

A tuning fork in air vibrates at 30 Hz with 5 cm amplitude. If the velocity of sound in air is 330 m · s^-1,

Amplitude, A = 5 cm = 0.05 m; frequency n = 30 Hz;

velocity, V = 330 m · s^-1

∴ Wavelength, \(\lambda=\frac{V}{n}=\frac{330}{30}=11 \mathrm{~m}\)

The expression for the generated traveling wave,

y = \(A \sin \frac{2 \pi}{\lambda}(V t-x)=0.05 \sin \frac{2 \pi}{11}(330 t-x) \mathrm{m}\)

Question 11. The path difference of two particles on a wave corresponding to a phase difference of 60° is

1. \(2 \lambda\)
2. \(\frac{\lambda}{2}\)
3. \(\frac{\lambda}{6}\)
4. \(\frac{\lambda}{3}\)

Answer:

The option 3 is correct.

Question 12. When sound enters water from air or vice-versa, which physical quantity of the waves remains unchanged?
Answer:

When sound enters water from air or vice-versa, the frequency of the waves remains unchanged.

Question 13. Two tuning forks vibrating simultaneously produce 5 beats per second. The frequency of one fork is 275 Hz. A small wax is attached to the other fork and 2 beats per second are produced when the two vibrate simultaneously. Find the frequency of the other fork.
Answer:

Given

Two tuning forks vibrating simultaneously produce 5 beats per second. The frequency of one fork is 275 Hz. A small wax is attached to the other fork and 2 beats per second are produced when the two vibrate simultaneously.

Let the frequency of the other fork be x.

Beat frequency = difference in the frequencies of the two tuning forks.

If x< 275 Hz, before waxing we have, 275 – x = 5 H or x = 270 Hz. After waxing, x will decrease, so the beat frequency will increase.

∴ x > 275 Hz and before waxing we have, x – 270 = 5

or x = 280 Hz. After waxing, A will decrease slightly, so the beat frequency will decrease to 2.

Progressive And Stationary Waves Class 11

Question 14. The velocity of sound in air at 20°C and 1 atm pressure is 344.2 m/s. At 40°C and 2 atm pressure, the velocity of sound in air is approximately

1. 350 m/s
2. 350 m/s
3. 303 m/s
4. 370 m/s

Answer:

If the velocities of sound are c₁ and c₂ at absolute temperatures T₁ and T₂, respectively, then

∴ \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}\)

Here, T₁ = 273 + 20 = 293 K and, T₂ = 273 + 40 = 313 K

∴ \(c_2=c_1 \times \sqrt{\frac{T_2}{T_1}}=344.2 \times \sqrt{\frac{313}{293}}\)

= 355.75 ≈ 356 m/s

The option 2 is correct.

Question 15. If the pressure, temperature, and density of an ideal gas are denoted by p, T, and ρ respectively, the velocity of sound in the gas is

1. Proportional to √p, when T is constant
2. Proportional to √T
3. Proportional to √p, when ρ is constant
4. Proportional to T

Answer:

Velocity of sound in air, \(\nu=\sqrt{\frac{\delta p}{\rho}}\)…(1)

or, \(\nu=\sqrt{\frac{\delta R T}{M}}\)…(2)

⇒ \(\left[because p V=R T \text { or, } p=\frac{R T}{V}=\frac{R T}{\frac{M}{\rho}}\right]\)

According to equation (1), v ∝ √p when ρ is constant.

According to equation (2), v ∝ √T

The options 2 and 3 are correct.

Transverse And Longitudinal Waves Class 11

Question 16. A uniform string of length 20 m is suspended from a rigid support. A short wave pulse is introduced at its lowest end. It starts moving up the string. The time taken to reach the support is

1. 2π√2 s
2. 2s
3. 2√2 s
4. √2s

Answer:

Tension at height y from the lowest end of the string, T = \(\frac{Mgy}{L}\)

[M is the mass of the string, L is the length of the string]

∴ The velocity of the wave at the height y of the string, \(\frac{d y}{d t}=\nu=\sqrt{\frac{T}{\mu}}\) [μ = mass per unit length of the string]

= \(\sqrt{\frac{\frac{M g y}{L}}{\frac{M}{L}}}=\sqrt{g y}\)

∴ \(\frac{d y}{\sqrt{y}}=\sqrt{g} d t\)

or, \(\int_0^L \frac{d y}{\sqrt{y}}=\sqrt{g} \int_0^t d t\)

or, \(\left.2 \sqrt{y}\right|_0 ^L=\left.\sqrt{g} t\right|_0 ^t\)

or, \(2 \sqrt{L}=\sqrt{g} t\)

∴ t = \(2 \sqrt{\frac{L}{g}}=2 \sqrt{\frac{20}{10}}=2 \sqrt{2} \mathrm{~s}\)

The option 3 is correct.

Characteristics Of Wave Motion Class 11

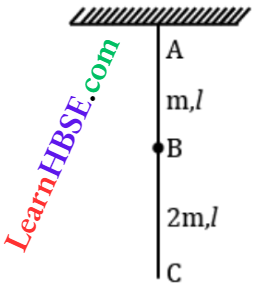
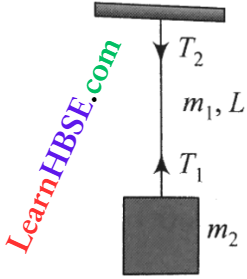
Question 17. A uniform rope of length L and mass m₁ hangs vertically from a rigid support. A block of mass m₂ is attached to the free end of the rope. A transverse pulse of wavelength λ₁ is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ₂. The ratio λ₂/λ₁ is

1. \(\sqrt{\frac{m_1+m_2}{m_2}}\)
2. \(\sqrt{\frac{m_2}{m_1}}\)
3. \(\sqrt{\frac{m_1+m_2}{m_1}}\)
4. \(\sqrt{\frac{m_1}{m_2}}\)

Answer:

Tension at the lower end of the rope, T₁ = m₂g

Tension at the top of the rope, T₂ = (m₁ + m₂)g

The velocity of the transverse wave, \(\nu=n \lambda=\sqrt{\frac{T}{\mu}}\)

[where n = frequency, λ = wavelength and μ = mass per unit length of the rope]

Hence, λ ∝ √T

∴ \(\frac{\lambda_1}{\lambda_2}=\sqrt{\frac{T_1}{T_2}}=\sqrt{\frac{m_2 g}{\left(m_1+m_2\right) g}}\)

= \(\sqrt{\frac{m_2}{m_1+m_2}}\)

or, \(\frac{\lambda_2}{\lambda_1}=\sqrt{\frac{m_1+m_2}{m_2}}\)

The option 1 is correct.

Wave Motion Formula Class 11

Question 18. A metal rod of 1 m in length, is dropped exactly vertically onto a hard metal floor. With an oscilloscope, it is determined that the impact produces a longitudinal wave of 1.2 kHz frequency. The speed of sound in the metal rod is

1. 600 m/s
2. 2400 m/s
3. 1800 m/s
4. 1200 m/s

Answer:

For the fundamental wave in the rod of length l, l \(=\frac{\lambda}{2}\)

Hence, Aλ =2l [l = wavelength]

∴ Velocity of sound,

V= nλ = (1.2 x 10³) x 2 x 1 = 2400 m/s

The option 2 is correct.

Question 19. The transverse harmonic wave on a string is described by Y(x,t) = 3.0sin(36t + 0.018x + π/4) where x and y are in cm and t is in second, The positive direction of x is from left to right,

1. Is this a traveling wave or a stationary wave? Give its direction of propagation.
2. What are its amplitude and frequency?
3. What is the initial phase at the origin?
4. What is the least distance between two successive crests in the wave?

Answer:

Compared with the general equation of a traveling wave,

y = a sin(ω- kx+ θ), we get, a = 3.0 cm,

ω = 36 Hz, k = -0.018 cm^-1 and \(\theta=\frac{\pi}{4}\)

1. The given equation corresponds to a traveling wave. As k is negative, the wave propagates along the negative x-direction.

2. Amplitude, a = 3.0 cm; frequency, \(\nu=\frac{\omega}{2 \pi}=\frac{36}{2 \times 3.14}=5.73 \mathrm{~Hz} .\)

3. Putting x = 0 and t = 0, we get

y = a sinθ = a sin \(\frac{\pi}{4}\)

So the initial phase at the origin = \(\frac{\pi}{4}\)

4. In magnitude, k = 0.018 cm^-1.

As k =\(\frac{2\pi}{\lambda}\), the wavelength,

∴ \(\frac{2\pi}{k}\) = 349 cm = least distance between two successive crests

Wave Motion Class 11 Important Questions

Question 20. What change is observed when a wave gets reflected from a hard and rigid support?
Answer:

• The reflected wave would propagate in the reverse direction, and
• Its phase would be reversed, i.e. a 180° phase difference would be introduced between the incident and the reflected waves.

Question 21. Though a violin note and a si tar note may have the same frequency, yet we can distinguish between the two notes. Explain how?
Answer:

• A violin note and a sitar note may have the same frequency or the same combination of frequencies. They may also have the same loudness.
• Yet, we can always distinguish between them because of a third property, which is essentially different for the two notes.
• This is the property called quality or timbre. The difference in timbre arises due to the distinct shapes of the waveforms associated with different musical notes.

Wave Motion Derivation Class 11 Physics

Question 22. If y = sin(3.6t + 0.018 x π/4) cm, find the amplitude and velocity of the wave.
Answer:

Given

y = sin(3.6t + 0.018 x π/4) cm

Comparing with the general equation y = asin(ωt -kx+θ) of a progressive wave, we get,

Amplitude, a = 3 cm,

Angular frequency, ω = 2πn = 3.6 Hz

and wave number, k = \(\frac{2 \pi}{\lambda}\) = -0.018 cm^-1

(The negative value means wave propagation in the negative x direction).

The velocity of the wave,

∴ V = \(n \lambda=\frac{2 \pi n}{\frac{2 \pi}{\lambda}}=\frac{\omega}{k}=\frac{3.6}{0.018}=200 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)