Collision Of A Falling Body With A Fixed Horizontal Plane
Example: Bouncing Of A Rubber Ball
Let a sphere be dropped from a height of h onto a horizontal plane at rest. After the impact with the plane, the sphere bounces up to a height H, (H< h). It falls again and after a second impact with the plane, the sphere comes to rest on the plane. These collisions are inelastic.
As the sphere is dropped from a height of h, the velocity v with which it strikes the plane,
v = √2gh …(1)
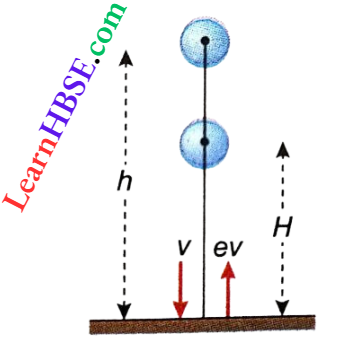
If the coefficient of restitution for the sphere-plane impact is e, the velocity of separation = ev. Hence, Work after the first Energy collision, the sphere rises up with the velocity ev. If it rises up to the height H, 0 = (ev)² – 2gh
or, H = \(\frac{e^2 \cdot 2 g h}{2 g}=e^2 h\)…(2)
If the collision was elastic, e = 1 and hence, H = h, i.e., the sphere would again rise up to h.
Collision Of A Falling Body With A Fixed Horizontal Plane
Total Distance Travelled Before Coming To Rest: After the first impact, the sphere rises up to a height H, given by (2). Then it falls from that height and causes a second impact with the plane. After the second impact, if the sphere rises up to a height H’ then from (2), the heights attained after the 2nd, 3rd, … impacts are respectively,
H’ = e²PH = e²-e²h = e4h,
H” = e²H’ = e² · e4h, and so on.
Hence, considering the up and down motions, the distance traveled, d, before coming to rest is given by the series.
d = \(h+2 e^2 h+2 e^4 h+2 e^6 h+\cdots \infty\)
= \(h+2 e^2 h\left(1+e^2+e^4+e^6+\cdots \infty\right)\)
= \(h+2 e^2 h \frac{1}{1-e^2}\)
[since the collisions are inelastic, \(e^2<1\) here.]
= \(h\left[1+\frac{2 e^2}{1-e^2}\right]\)
= \(h \frac{1+e^2}{1-e^2}\)…(3)
Time Taken To Reach The Steady State: Let t0 denote the time taken by the sphere to come down from the height h.
∴ h = \(\frac{g t_0^2}{2} \quad \text { or, } t_0=\sqrt{\frac{2 h}{g}}\)
If the time interval between the first and the second impacts is T, then,
0 = \(e v \cdot T-\frac{g T^2}{2}\)
or, \(g T^2=2 e v T\)
or, \(T=\frac{2 e v}{g}=\frac{2 e \sqrt{2 g h}}{g}=2 e \sqrt{\frac{2 h}{g}}\)
Similarly, if T’ is the time interval between the second and the third impacts, then
T’ = \(2 e^2 \sqrt{\frac{2 h}{g}}\)
Hence, the total time r taken by the sphere to reach the steady state,
t = \(\sqrt{\frac{2 h}{g}}+2 e \sqrt{\frac{2 h}{g}}+2 e^2 \sqrt{\frac{2 h}{g}}+\cdots+\infty\)
= \(\sqrt{\frac{2 h}{g}}\left[1+2 e+2 e^2+\cdots+\infty\right]\)
= \(\sqrt{\frac{2 h}{g}}\left[1+2 e\left(1+e+e^2+\cdots+\infty\right)\right]\)
= \(\sqrt{\frac{2 h}{g}}\left[1+\frac{2 e}{1-e}\right]\)
= \(\sqrt{\frac{2 h}{g}}\left(\frac{1+e}{1-e}\right)\)
Elastic And Inelastic Collision Of A Falling Body
The Value Of The Coefficient Of Restitution: From the relation H = e²h, e can be calculated by measuring H and h. However, if the same rubber ball is dropped from the same height h, it might not bounce up to H every time. Hence, the value of e determined by this method is an approximate one.
Impulse Of The Force Applied By The Plane: Let the mass of the sphere be m, downward velocity (while falling from a height h) just before the first impact be v, and upward velocity just after the impact be ev.
Hence, impulse of the upward force applied by the plane
= change in momentum
= m[ev-(-v)] = mv(1 + e)
= m√2gh[1 + e]
The Loss Of Kinetic Energy: The loss of kinetic energy due to the first impact
= \(\frac{1}{2}\) mv2 – \(\frac{1}{2}\)m(ev)²
= \(\frac{1}{2}\)mv(1-e²) = \(\frac{1}{2}\)m . 2gh(1-e²)
= mgh(1 – e²)
Work And Energy – Collision Of A Falling Body With A Fixed Horizontal Plane Numerical Examples
Example 1. A glass ball is dropped from a height of 15 m onto a horizontal glass plate at rest Find the upward rise of the ball after impact The coefficient of restitution e = 0.6.
Solution:
Given
A glass ball is dropped from a height of 15 m onto a horizontal glass plate at rest
If the ball falls from a height h onto a horizontal plane and rises up to H after impact, then H = e²h = (0.8)³ x 15 = 9.6 m.
Example 2. A ball is dropped from a height of 90 m onto a horizontal plane at rest. Find the total distance traveled by it before coming to rest. The coefficient of restitution, e = 0.5.
Solution:
Given
A ball is dropped from a height of 90 m onto a horizontal plane at rest.
Total distance travelled by the ball
= \(h \times \frac{1+e^2}{1-e^2}=90 \times \frac{1+(0.5)^2}{1-(0.5)^2}\)
= \(90 \times \frac{1.25}{0.75}=150 \mathrm{~m} .\)
Coefficient Of Restitution Class 11 Physics
Example 3. A ball is dropped from a height of 1 m onto a horizontal plane. The ball takes 1.3 seconds from its time of release for the second impact with the plane. Find the coefficient of restitution.
Solution:
Given
A ball is dropped from a height of 1 m onto a horizontal plane. The ball takes 1.3 seconds from its time of release for the second impact with the plane.
Let the velocity of the ball be V just before the 1st impact with the plane.
Then V² = 2gh = 2 x 980 x 100
or, V = \(\sqrt{2 \times 980 \times 100}=442.7 \mathrm{~cm} \cdot \mathrm{s}^{-1} \text {. }\)
If the time taken by the ball is r, to fall from the height of 1 m, then
t1 = \(\sqrt{\frac{2 h}{g}}\left[\text { using } h=\frac{1}{2} g t^2\right]\)
= \(\sqrt{2 \times \frac{100}{980}}=0.452 \mathrm{~s} .\)
So, the time interval between the first and the second impacts = 1.3 – 0.452 = 0.848 s.
The time taken by the ball to reach the highest point after the first impact is, t1 = \(\frac{1}{2}\) x 0.848 = 0.424 s
If the velocity of separation of the ball after the first impact is v, then
0 = v – gt1
or, v – gt1 = 980 x 0.424 = 415.5 cm · s-1
∴ Coefficient of restitution,
e = \(\frac{v}{V}=\frac{415.5}{442.7}=0.94\)
Numerical Problems On Collision Of Falling Objects
Example 4. A bullet of mass m hits a wooden block of mass M, suspended by a string of length l, and gets embedded In It. If the velocity of the bullet is v, find the angular displacement of the block.
Solution:
Given
A bullet of mass m hits a wooden block of mass M, suspended by a string of length l, and gets embedded In It. If the velocity of the bullet is v
Let the velocity of the block-bullet system after impact be V and the angular displacement be θ.
From the law of conservation of momentum,
mv = \((M+m) V \quad \text { or, } V=\frac{m v}{M+m}\)
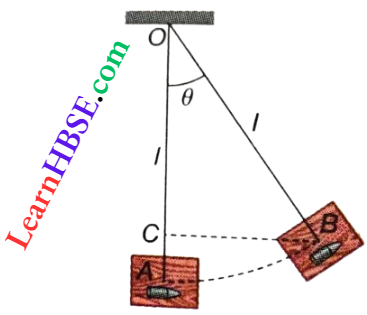
The kinetic energy of the block-bullet system at position A
= \(\frac{1}{2}(M+m) V^2\)
= \(\frac{1}{2}(M+m) \times \frac{m^2 v^2}{(M+m)^2}\)
= \(\frac{m^2 v^2}{2(M+m)}\)
The potential energy of the system at B
= \((M+m) g \cdot A C\)
= \((M+m) g[O A-O C]\)
= \((M+m) g(l-l \cos \theta)=(M+m) g l(1-\cos \theta)\)
From the law of conservation of energy, \(\frac{1}{2} \frac{m^2 v^2}{M+m}=(M+m) g l(1-\cos \theta)\)
or, \(1-\cos \theta=\frac{1}{2} \frac{m^2 v^2}{(M+m)^2 g l}\)
or, \(2 \sin ^2 \frac{\theta}{2}=\frac{1}{2}\left(\frac{m v}{M+m}\right)^2 \times \frac{1}{g l}\)
or, \(\sin \frac{\theta}{2}=\frac{m v}{2(M+m) \sqrt{g l}} or, \frac{\theta}{2}=\sin ^{-1}\left[\frac{m v}{2(M+m) \sqrt{g l}}\right]\)
∴ \(\theta=2 \sin ^{-1}\left[\frac{m v}{2(M+m) \sqrt{g l}}\right] .\)
Derivation Of Velocity After Collision Of A Falling Body
Example 5. A boy of mass m1, standing on a smooth horizontal surface, throws a sphere of mass m2 parallel to the surface. After a time t, If the separation between them becomes x, then show that the work done by the boy In throwing the sphere = \(\frac{1}{2}\left(\frac{x}{t}\right)^2\left(\frac{m_1 m_2}{m_1+m_2}\right)\)
Solution:
Given
A boy of mass m1, standing on a smooth horizontal surface, throws a sphere of mass m2 parallel to the surface. After a time t, If the separation between them becomes x,
Let v denote the velocity of the sphere, and V denote the velocity of the boy, due to reaction. From the law of conservation of momentum,
m1V = m2v…(1)
Separation between them after a time t, x = (V+ v)t…(2)
From (1) and (2) we get, \(\frac{m_2}{m_1} v+v=\frac{x}{t} \quad \text { or, } v=\frac{x}{t} \cdot \frac{m_1}{m_1+m_2}\)
Similarly, \(V=\frac{x}{t} \cdot \frac{m_2}{m_1+m_2}\)
Work done in throwing the sphere = sum of kinetic energies of the sphere and the boy
= \(\frac{1}{2} m_1 V^2+\frac{1}{2} m_2 v^2\)
= \(\frac{1}{2} m_1\left(\frac{x}{t}\right)^2 \cdot \frac{m_2^2}{\left(m_1+m_2\right)^2}+\frac{1}{2} m_2\left(\frac{x}{t}\right)^2 \frac{m_1^2}{\left(m_1+m_2\right)^2}\)
= \(\frac{1}{2}\left(\frac{x}{t}\right)^2 \frac{m_1 m_2}{\left(m_1+m_2\right)^2}\left(m_1+m_2\right)\)
= \(\frac{1}{2}\left(\frac{x}{t}\right)^2 \cdot \frac{m_1 m_2}{m_1+m_2}\)
Example 6. Two blocks mx and m2 of masses 2 kg and 5 kg, respectively, are moving on a smooth plane along a straight line in the same direction, with velocities 10 m · s-1 and 3m · s-1 respectively. The block mg is situated ahead of the block. An ideal spring (k = 1120 N · m-1) is attached to the back of the block m2. Find the compression of the spring when m1 collides with m2.
Solution:
Given
Two blocks mx and m2 of masses 2 kg and 5 kg, respectively, are moving on a smooth plane along a straight line in the same direction, with velocities 10 m · s-1 and 3m · s-1 respectively. The block mg is situated ahead of the block. An ideal spring (k = 1120 N · m-1) is attached to the back of the block m2.
Let initial velocities of blocks m1 and m2 be v1 and v2 respectively. After the collision, the two blocks combine and move with a velocity V.
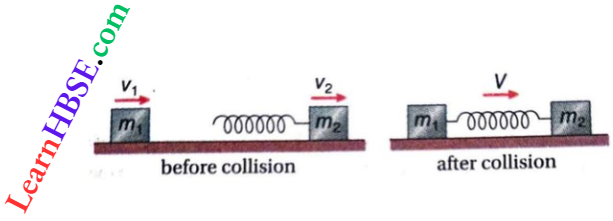
From the law of conservation of momentum, \(m_1 v_1+m_2 v_2=\left(m_1+m_2\right) V\)
or, \(2 \times 10+5 \times 3=(2+5) V\)
V = \(5 \mathrm{~m} \cdot \mathrm{s}^{-1}\)
Suppose the spring is compressed by x.
From the law of conservation of energy, we get total energy before collision = total energy after collision
or, total kinetic energy of the blocks = kinetic energy of the combined blocks + potential energy of the compressed spring
i.e., \(\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2=\frac{1}{2}\left(m_1+m_2\right) V^2+\frac{1}{2} k x^2\)
or, \(2 \times(10)^2+5 \times(3)^2=7 \times(5)^2+1120 \times x^2\)
∴ \(x^2=\frac{1}{16}\)
or, x = \(\frac{1}{4}=0.25 \mathrm{~m}\).
Energy Loss In Collision Of A Falling Object
Example 7. A ball moving at 9 m · s-1, collides with an identical ball at rest. After the collision, both the balls scatter at 30° with the initial direction of motion. Find the velocity of each ball after collision. Does the kinetic energy remain conserved in such a collision?
Solution:
Given
A ball moving at 9 m · s-1, collides with an identical ball at rest. After the collision, both the balls scatter at 30° with the initial direction of motion.
Let mass of each ball = m. Velocities of the two balls before collision, u1 = 9 m · s-1 and u2 = 0.
Let their velocities after collision be v1 and v2 respectively.
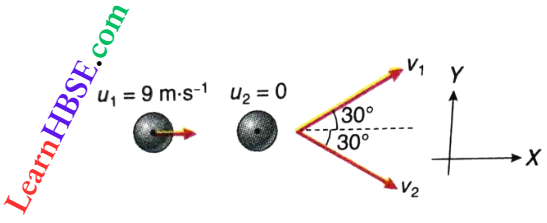
From the law of conservation of the x and y components of momentum,
9m+ 0 = mv1 cos 30° + mv2 cos 30°…(1)
and 0 = mv1 sin30° – mv2 sin 30°…(2)
From (1), \(v_1+v_2=\frac{18}{\sqrt{3}}\)…(3)
and from (2), v1 – v2 = 0…(4)
Solving (3) and (4), v1 = v2 = 373 m · s-1
Initial kinetic energy = \(\frac{1}{2} m u_1^2+\frac{1}{2} m u_2^2\) = \(\frac{1}{2} m\left(9^2+0\right)=\frac{81}{2} m\)
Final kinetic energy = \(\frac{1}{2} m v_1^2+\frac{1}{2} m v_2^2\) = \(\frac{1}{2} m(27+27)=27 m\)
Hence, kinetic energy does not remain conserved in this case.
Example 8. Two identical blocks A and B, each of mass m, are connected to each other with a spring of length L. The Force constant of the spring is k. The system is kept on a horizontal table. An identical third block C moving with a velocity v along the line AB collides with A elastically,
- What is the kinetic j energy of the system A-B in the most compressed state?
- What is the maximum compression of the spring?
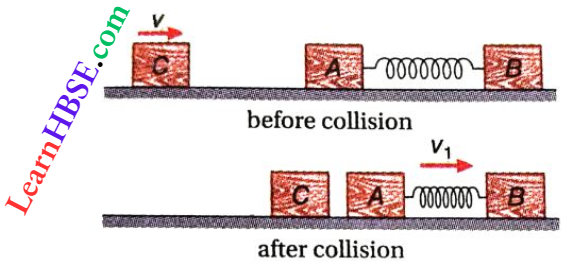
Solution:
1. The velocity of block C, just before collision = v. As the collision of C with A is elastic, block C comes to rest just after collision, and block A gets the velocity v in the forward direction.
Because of the spring between A and B, the velocity of A gradually decreases, but that of B gradually increases, and the spring is compressed.
As soon as velocities of the blocks A and B become equal, the spring attains maximum compression, and system A-B begins to move with a common velocity v1.
From the law of conservation of momentum, mv = 2m x v1.
or, \(v_1=\frac{\nu}{2}\)
∴ At maximum compression of the spring, the kinetic energy of the system A-B
= \(\frac{1}{2}(2 m) v_1^2=\frac{1}{2} \times 2 m \times \frac{v^2}{4}=\frac{1}{4} m v^2\)
2. If the maximum compression of the spring is x, then potential energy of the compressed spring
= \(\frac{1}{2} k x^2=\frac{1}{2} m v^2-\frac{1}{4} m v^2=\frac{1}{4} m v^2\)
or, \(x^2=\frac{m}{2 k} v^2\)
or, \(x=v \sqrt{\frac{m}{2 k}}\)
Rebound Velocity Of A Falling Body After Collision
Example 9. A mass 2m is at rest and another mass m is moving with a velocity. An elastic collision takes place between them. Show that the mass m loses 8/9 part of its initial kinetic energy in this collision.
Solution:
Given
A mass 2m is at rest and another mass m is moving with a velocity. An elastic collision takes place between them.
Let the velocity of mass m before collision =u and the velocity of mass m after collision = v1.
The velocity of mass 2m after collision = v2.
From the law of conservation of momentum, \(m u=m v_1+2 m v_2 \quad \text { or, } u=v_1+2 v_2\)
or, \(u-v_1=2 v_2\)…(1)
From the law of conservation of energy, \(\frac{1}{2} m u^2=\frac{1}{2} m v_1^2+\frac{1}{2}(2 m) v_2^2\)
or, \(u^2=v_1^2+2 v_2^2 or, u^2-v_1^2=2 v_2^2\)
or, \(\left(u+v_1\right)\left(u-v_1\right)=2 v_2^2\)…(2)
Dividing (2) by (1), we get, \(u+v_1=v_2\)….(3)
From (1) and (3) we get, \(v_2=\frac{2}{3} u\)
∴ \(v_1=-\frac{1}{3} u\)
Initial kinetic energy of the mass \(m=\frac{1}{2} m u^2\).
Its kinetic energy after collision \(=\frac{1}{2} m v_1^2=\frac{1}{2} m \cdot \frac{1}{9} u^2=\frac{1}{18} m u^2\)
Hence, decrease in kinetic energy
= \(\frac{1}{2} m u^2-\frac{1}{18} m u^2=\frac{8}{9} \times \frac{1}{2} m u^2\)
= \(\frac{8}{9}\) of its initial kinetic energy
Motion And Impact Of Falling Bodies Class 11
Example 10. Two flat discs A and B are kept on a smooth horizontal table. The disc A moves with a velocity u and makes a perfectly elastic collision with B. If the mass of A is k times the mass of B, using conservation laws, find the fraction of kinetic energy of A transferred from A to B. Also prove that if the mass of B was k times the mass of A, the fraction of kinetic energy transferred would have been the same.
Solution:
Given
Two flat discs A and B are kept on a smooth horizontal table. The disc A moves with a velocity u and makes a perfectly elastic collision with B. If the mass of A is k times the mass of B, using conservation laws,
Let mass of disc A be m1 and that of disc B = m2.
∴ m1 = km2
Let the velocities of A and B after collision be v1 and v2, respectively. From the law of conservation of momentum, \(m_1 u+0=m_1 v_1+m_2 v_2\)
or, \(k m_2 u=k m_2 v_1+m_2 v_2\)
∴ \(k\left(u-v_1\right)=v_2\)…(1)
As the collision is perfectly elastic, the kinetic energy is also conserved.
∴ \(\frac{1}{2} m_1 u^2+0=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\)
or, \(k\left(u^2-v_1^2\right)=v_2^2\)….(2)
From equation (1), \(v_2^2=k^2\left(u-v_1\right)^2\)…(3)
Dividing (3) by (2), 1 = \(\frac{k\left(u-v_1\right)}{u+v_1} \quad \text { or, } v_1=\left(\frac{k-1}{k+1}\right) u\)…(4)
Kinetic energy of A before collision \(E_1=\frac{1}{2} m_1 u^2=\frac{1}{2} k m_2 u^2\)
Kinetic energy of A after collision \(E_2=\frac{1}{2} m_1 \nu_1^2=\frac{1}{2} k m_2\left(\frac{k-1}{k+1}\right)^2 u^2\)
∴ Loss in kinetic energy, \(E_1-E_2=\frac{1}{2} k m_2 u^2\left[1-\left(\frac{k-1}{k+1}\right)^2\right]\)
= \(\frac{1}{2} k m_2 u^2 \cdot \frac{4 k}{(k+1)^2}\)
∴ Fraction of kinetic energy of A transferred to B,
x = \(\frac{E_1-E_2}{E_1}=\frac{4 k}{(k+1)^2}\)….(5)
If \(m_1=\frac{m_2}{k}\) (second case), k is to be replaced by \(\frac{1}{k}\) in expression (5). Then
y = \(\frac{4 \times \frac{1}{k}}{\left(\frac{1}{k}+1\right)^2}=\frac{4 k}{(k+1)^2}\)…(6)
Hence, in both cases, the same fraction of kinetic energy of A is transferred to B.
Collision With A Fixed Surface Physics Class 11
Example 11. A small ball A travels In a vertical plane along a quarter of a circular path of radius 10 cm, as shown, and hits another ball B of the same mass at rest Considering the collision to be elastic, and neglecting frictional force, find the velocity of each ball after the collision.
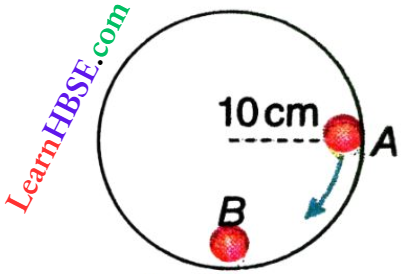
Solution:
Given
A small ball A travels In a vertical plane along a quarter of a circular path of radius 10 cm, as shown, and hits another ball B of the same mass at rest Considering the collision to be elastic, and neglecting frictional force
Let the mass of each ball be m and the velocity of A just before it collides with B be u.
From the conservation of energy of A, \(\frac{1}{2} m u^2=m g h\)
or, \(u=\sqrt{2 g h}=\sqrt{2 \times 980 \times 10}=140 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)
In an elastic collision, two bodies of equal masses exchange their velocities. Hence, after the collision, A will come to rest, and B will move with a velocity 140 cm · s-1.
Example 12. A fire brigade pump draws water from a reservoir 2 m below the ground. It hurls the stream of water at 50 kg per second. This water stream strikes the top of a 8 m high wall, at a speed of 5 m· s-1. Determine the power of the pump.
Solution:
Given
fire brigade pump draws water from a reservoir 2 m below the ground. It hurls the stream of water at 50 kg per second. This water stream strikes the top of a 8 m high wall, at a speed of 5 m· s-1
Water is raised through a height of 2 + 8 = 10 m
Total work done = total energy gained by the water = potential energy + kinetic energy
= mgh + \(\frac{1}{2}\)mv
The pump provides this energy.
∴ Work done by pump in one second
= 50 x 9.8 x 10 + \(\frac{1}{2}\) x 50 x 52 =50(98 + 12.5) = 5525 J
∴ Power of the pump = 5525 W = 5.525 kW.
Example 13. A vertical spring fixed at its upper end can be elon¬gated by 2 cm under the action of a stretching force of (80 g)g. A body of mass 600 g is attached to its free end, and then the system is displaced from its equilibrium position by 8 cm. Find the energy of the system at this position. The mass is then released. If the energy is conserved, find the velocity of the body 4 cm away from its equilibrium position, [g = 1000 cm · s-2]
Solution:
Given
A vertical spring fixed at its upper end can be elon¬gated by 2 cm under the action of a stretching force of (80 g)g. A body of mass 600 g is attached to its free end, and then the system is displaced from its equilibrium position by 8 cm.
Spring constant, k = \(\frac{80 g}{2}\) x 40 x 1000 = 40000 dyn · cm-1
Elongation of the spring due to a force of (80 g)g = 2 cm
∴ Extension of the spring due to the mass of 600 g = \(\frac{2 \times 600}{80}\) = 15 cm.
The potential energy of the spring at this stage
= \(\frac{1}{2} k x^2=\frac{1}{2} \cdot 40000 \cdot(15)^2=45 \times 10^5 \mathrm{erg}\)
The energy required for a further 8 cm elongation
= \(\frac{1}{2}\) x 40000 x 8² = 12.8 x 105 erg
Total energy of the system = (45 x 105 + 12.8 x 105) = 57.8 x 105 erg.
Again, potential energy for a displacement of 4 cm from the equilibrium position
= \(\frac{1}{2}\) x 40000 x 42 = 3.2 x 105 erg
∴ Kinetic energy in this condition = 12.8 x 105 – 3.2 x 105 = 9.6 x 105 erg.
If the velocity of the body is v, then \(\frac{1}{2} m v^2=9.6 \times 10^5 \quad \text { or, } v^2=\frac{2 \times 9.6 \times 10^5}{600}\)
or, v = 56.568 cm · s-1.
Physics Of Falling Objects And Collisions
Example 14. A conveyor belt, run by a motor, is moving at a constant speed of 5 m · s-1. If 5 kg of sand is sprinkled per second on the belt, then what extra power should the motor supply to the belt?
Solution:
Given
A conveyor belt, run by a motor, is moving at a constant speed of 5 m · s-1. If 5 kg of sand is sprinkled per second on the belt
The initial horizontal speed of sand before falling on the conveyor belt = 0.
So, the rate of supply of kinetic energy to the sand by the belt
= \(\frac{1}{2} \times \frac{\text { mass } \times \text { velocity }}{2}=\frac{1}{2} \times \frac{5 \times 5^2}{1}=62.5 \mathrm{~J} \cdot \mathrm{s}^{-1}\)
If there is no loss of energy otherwise, then extra power to be supplied to the belt by the motor = 62.5 J · s-1 or 62.5 W.
Example 15. A pump can raise 100 L of water per minute to a height of 10 m. What should be the power of the pump?
Solution:
Given
A pump can raise 100 L of water per minute to a height of 10 m.
Mass of 100 L of water, m = 100 x 103 g = 100 kg
Potential energy gained by the water per minute, V = mgh =100 x 9.8 x 10 = 9800 J
∴ Power of the pump = \(\frac{9800}{60}=163.3 \mathrm{~J} \cdot \mathrm{s}^{-1}=163.3 \mathrm{~W}\)
Coefficient Of Restitution Formula For Falling Body
Example 16. A conservative force acting on a particle is F = -Ax+ Bx² where A and B are constants and x i is in m. Find the potential energy associated with the force.
Solution:
Given
A conservative force acting on a particle is F = -Ax+ Bx² where A and B are constants and x i is in m.
F = -Ax+Bx²
∴ Potential energy, U = \(-\int F d x=-\int\left(-A x+B x^2\right) d x\)
= \(-\left[-\frac{A x^2}{2}+\frac{B x^3}{3}\right]+C\) [where C is a constant]
= \(\frac{A x^2}{2}-\frac{B x^3}{3}+C\)
