Haryana Board Class 6 Maths Solutions For Chapter 11 Algebra

Haryana Board Class 6 Maths Solutions For  Chapter 11 Algebra

• The branch of mathematics in which we study numbers is arithmetic.
• The branch of mathematics in which we study shapes is geometry.
• ‘n’ is an example of a variable. Its value is not fixed. It can take any value 1,2,3,4…
• The main feature of algebra is the use of letters or alphabet to represent numbers.
• We can make different patterns and shapes using match sticks. The relation between the patterns and number of sticks used is observed to frame rules.
• Number of matchsticks required = 3x No. of triangles to be formed.
• We may use any letter (small case alphabet) a, b, m, n, p, q, x, y, z etc…… to represent a variable.
• An expression is made up of variables and constants using different operations.
  Eg: 2x, 3m – 1, 3s + 7, 8p, \(\frac{y}{3}\) etc..
• Variables allow us to express many common rules of geometry and arithmetic in a more general way.
• A mathematical statement consisting of an equal symbol between two algebraic expressions that have the same value is called ‘Algebraic Equation’.
  Eg: 3m = 12, 2x + 1 = 10, 3p + 5 = 2p + 6….. etc.,
• Algebra is a powerful tool for solving ‘puzzles’, ‘riddles’ and problems in our daily life.

Haryana Board Class 6 Maths Solutions For  Chapter 11 Algebra Exercise 11.1

Question 1. Find the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.

a) A pattern of letter T as T

b) A pattern of letter Z as Z

c) A pattern of letter U as U

d) A pattern of letter V as V

e) A pattern of letter E as E

f) A pattern of letter S as S

g) A pattern of letter A as A

Solution. a) Number of matchsticks required = 2n

b) Number of matchsticks required = 3n

c) Number of matchsticks required =3n

d) Number of matchsticks required = 2n

e) Number of matchsticks required = 5n

f) Number of matchsticks required = 5n

g) Number of matchsticks required = 6n

Haryana Board Class 6 Maths Algebra Solutions

Question 2. We already know the rules for the pat- tern of letters L, C and F. Some of the letters from Q. 1 (given above) give us the same rule as that given by L. Which are these? Why does this happen?

Solution. The letters T and V that has pattern 2n, since 2 match sticks are used in all these letters.

Question 3. Cadets are marching in a parade. There are 5 cadets in a row. What is the rule which gives the number of cadets, given the number of rows? (Use ‘n’ for the number of rows.)

Solution. Number of cadets = 5n

Question 4. If there are 50 mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? (Use ‘b’ for number of boxes.)

Solution. Total number of mangoes = 50 b.

Question 5. The teacher distributes 5 pencils per student. Can you tell how many pencils are needed, given the number of students? (Use’s ‘for the number of students.)

Solution. Number of pencils needed = 5 s.

Question 6. A bird flies 1 kilometer in one minute. Can you express the distance covered by the bird in terms of its flying time in minutes. (Use t’ for flying time in minutes)

Solution. Distance covered by the bird in t minutes = t kilometres.

Question 7. Radha is drawing a dot Rangoli (a beautiful pattern of lines joining dots with chalk powder. She has 9 dots in a row. How many dots will her Rangoli have for r rows? How many dots are there if there are 8 rows? If there are 10 rows?

Solution. Number of dots her Rangoli will have for ‘r’ rows = 9r.

Number of dots if there are 8 rows = 8 x 9 = 72.

Number of dots if there are 10 rows = 10 × 9 = 90.

Class 6 HBSE Maths Chapter 11 Algebra Important Questions

Question 8. Leela is Radha’s younger sister. Leela is 4 years younger than Radha. Can you write Leela’s age in terms of Radha’s age? Take Radha’s age to be x years.

Solution. Radha’s age = x years.

Leela’s age = (x – 4) years

Question 9. Mother has made laddus. She gives some laddus to guests and family members; still 5 laddus remain. If the number of laddus mother gave away is 1, how many laddus did she make?

Solution. Number of laddus she made l + 5.

Question 10. Oranges are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still 10 oranges remain outside. If the number of oranges in a small box are taken to be x, what is the number of oranges in the larger box?

Solution. Number of oranges in the larger box = 2x + 10.

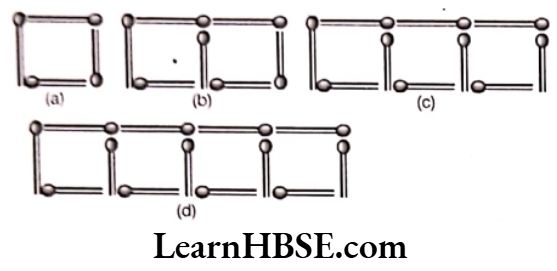
Question 11. a) Look at the following matchstick pattern of squares. The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares.

(Hint: If you remove the vertical stick at the and you will get a pattern of CS)

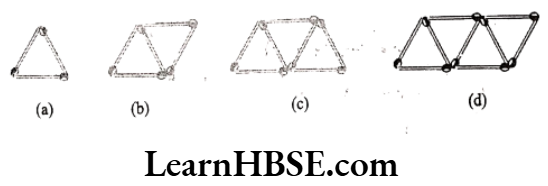
b) Gives a matchstick pattern of triangles. As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.

Solution. a) Number of matchsticks = 3n + 1, n= number of squares.

b) Number of matchsticks = 2n + 1, n = number of triangles.

Haryana Board Class 6 Maths Solutions For  Chapter 11 Algebra Very Short Answer Questions

Question 1. Make a rule between the number of blades required and the number of fans (say n) in a hall?

Solution. A rule between the number of blades required and number of fans (say n) in a hall is 3n.

Question 2. Harshini says that she has 5 biscuits more than Padma has. How can you express the relationship using the variable ‘y’?

Solution. Let the number of biscuits that Padma has = ‘y’.

Harshini says that she has 5 biscuits morethan Padma has.

∴ Number of biscuits that Harshini has = y + 5

Solving Simple Equations Class 6 Haryana Board

Question 3. Prabhakar has ‘p’ number of balls. Number of balls with Devi is 3 times the balls with Prabhakar. Write this as an expression.

Solution. Number of balls that Prabhakar has = p Devi has 3 times of the balls with Prabhakar

∴ The required expression is = 3 x p = 3p

Question 4. Find the general rule for the perimeter of a rectangle. Use variables ‘l’ and ‘b’ for length and breadth of the rectangle respectively.

Solution. Length of the rectangle = 1 units

Breadth = b units

Perimeter = 1 + b + 1 + b

= 21 + 2b

= 2(1 + b) units

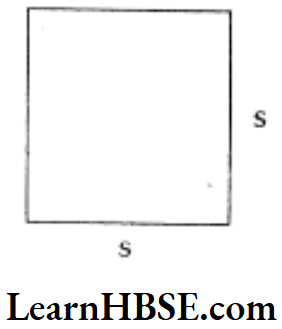
Question 5. Find the general rule for the area of a square by using the variable ‘s’ for the side of a square.

Solution. Side of a square = s units

Area of a square = side x side = s x s

= s2 square units

Algebraic Expressions Class 6 HBSE Notes

Haryana Board Class 6 Maths Solutions For  Chapter 11 Algebra Short Answer Questions

Question 1. Arrange 2 matchsticks to form the shape

Continue the same shape for 2 times, 3 times and 4 times. Frame the rule for repeating the pattern.

Solution.

Number of matchsticks required for shape – 1 is 2 = 2 × 1 = 2 × 1 times

Number of matchsticks required for shape – 2 is 4 = 2 x 2 = 2 × 2 times

Number of matchsticks required for shape – 3 is 6= 2 × 3 = 2 × 3 times

Number of matchsticks required for shape – 4 is 8.2 x 4 = 2 × 4 times

∴ The rule for number of matchsticks required for n times for the shape is = [2 x n] times.

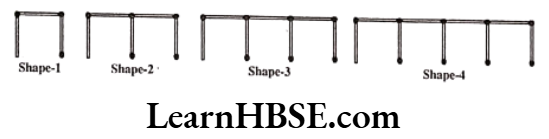
Question 2. A line of shapes is constructed using matchsticks.

Basic Algebra Problems For Class 6 With Solutions

1) Find the rule that shows how many sticks are needed to make a line of such shapes.

Solution.

∴ Number of matchsticks = 2 x (Number of shapes) + 1

Let s = Number of shapes

m = Number of matchsticks

∴ Number of matchsticks = m = 2s + 1

2) How many matchsticks are needed to form shape 12 ?

Solution. Number of matchsticks needed to form shape 12

= 2 × 12 + 1

= 24 + 1 = 25

Question 3. Find the rule which gives the number of matchsticks required to make the following matchstick patterns.

1) A pattern of letter ‘T’

2) A pattern of letter ‘E’

3) A pattern of letter ‘Z’

Solution. 1)

Number of matchsticks required to make a pattern of letter ‘T’ is 3

∴ The rule is 3 m.

2)

Number of matchsticks required to make a

pattern of letter ‘E’ is 4

∴ The rule is 4m

Word Problems On Algebra For Class 6 Haryana Board

3)

Number of matchsticks required to make a

pattern of letter ‘Z’ is 3

∴ The rule is 3m

Question 4. Find a rule for the following pattern between number of shapes formed and number of matchsticks required.

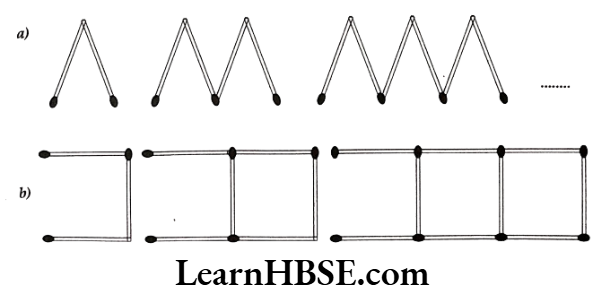
Solution. a) Number of match sticks used for this pattern is 2, 4, 6, ……… Rule is – 2n

b) Number of match sticks used for this pattern is 3, 6, 9, …… Rule is – 3n

Question 5. 1) How many match sticks are required to form a triangle?

Solution. To make a triangle 3 match sticks are required.

2) Complete the following table: Write the rule.

Solution. The rule is “number of matchsticks required = 3 times the number of triangles to be formed.”

Question 6. 1) How many matchsticks are required to form a square?

Solution. To make a square 4 matchsticks are required..

2) Complete the following table: Write the rule.

Solution. The rule is “Number of matchsticks required = 4 times number of squares to be formed”.

Haryana Board Class 6 Maths Solutions For  Chapter 11 Algebra Long Answer Questions

Question 1. Rita took matchsticks to form the shape

She repeated the pattern and gave a rule

Number of matchsticks needed = 6.y, where y is the number of shapes to be formed.

Is it correct? Explain.

What is the number of sticks needed to form 5 such shapes?

Solution.

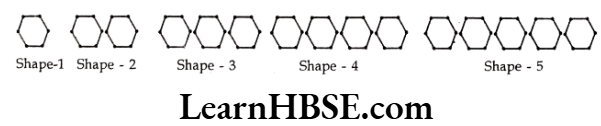
Number of match sticks required for shape – 1 is 6 = 6 × 1 times

Number of match sticks required for shape – 2 is 12 = 6 x 2 times

Number of match sticks required for shape – 3 is 18 = 6 x 3 times

Number of match sticks required for shape – 4 is 24 = 6 × 4 times

Number of match sticks required for shape 5 is 30 = 6 x 5 times

∴ Number of match sticks needed for the shape y is = 6 x y

[Where y is the number of shapes to be formed]

Yes, Rita is correct.

Number of match sticks needed to form 5 shapes = 6 x 5 = 30

Question 2. Find the nth term in the following sequences

(1),3,6,9,12,…

(2) 2,5,8,11,…

(3) 1, 4, 9, 16,…

Solution. 1) 3,6,9,12.

3 = 3 × 1

6 = 3 × 2

9 = 3 × 3

12 = 3 × 4

n^th term of the sequence = 3 x n

[∴ n is a natural number]

2) 2,5,8,11

2 = 3 x 1 – 1

5 = 3 × 2 – 1

8 = 3 × 3 – 1

11 = 3 x 4 – 1

n^th term of the sequence = 3 x n – 1

[∴ n is a natural number]

3) 1, 4, 9, 16……………….

1 = \(\mathrm{1}^2\)

4 = \(\mathrm{2}^2\)

9 = \(\mathrm{3}^2\)

16 = \(\mathrm{4}^2\)

n^th term of the sequence = \(\mathrm{n}^2\)

[∴ n is a natural number]

Haryana Board Class 6 Maths Solutions For  Chapter 11 Objective Type Questions

Choose the correct answer :

Question 1. The symbol used in equation is

1. >
2. =
3. <
4. ≠

Answer. 2. =

Question 2. How many sticks are needed to prepare the letter Z?

1. 6
2. 7
3. 2
4. 3

Answer. 4. 3

Question 3. 2, 4, 6, ……… nth term is …………

1. \(\frac{n}{2}\)
2. 2n
3. 4n
4. \(\mathrm{n}^2\)

Answer. 2. 2n

Class 6 Maths Variables And Constants Explained

Question 4. Statement – A: An expression is made up of variables and constants using different operations.

Statement – B: A mathematical statement consisting of an equal symbol between two algebraic expressions is called ‘Algebraic equation’

1. Both A & B are true
2. A is true, B is false
3. A is false, B is true
4. Both A & B are false

Answer. 1. Both A & B are true

Question 5. Write the statement for the expression 3m + 11

1. 11 more than three times of m
2. 11 is added to thrice the m
3. 11 times more than thrice them
4. Both A & B

Answer. 4. Both A & B

Question 6. Statement – A: Solution of an equation is the value of the variable for which LHS and RHS are equal.

Statement – B: The solution is also called root of the equation.

1. Both A & B are true
2. A is true, B is false
3. A is false, B is true
4. Both A & B are false

Answer. 1. Both A & B are true

Question 7. 3, 6, 9, 12 ………. nth term is

1. 2n
2. n + 3
3. 3n
4. \(\frac{n}{3}\)

Answer. 3. 3n

Question 8. The nth term of 2, 5, 8, 11 …….

1. 3n
2. 3n – 1
3. 3n + 1
4. 2n + 1

Answer. 2. 3n – 1

Question 9. The nth term of 1, 4, 9, 16 ……..

1. \(\mathrm{n}^2\)
2. 2n
3. 2n – 1
4. n + 2

Answer. 1. \(\mathrm{n}^2\)

Haryana Board Class 6 Maths Solutions For  Chapter 11 Algebra Fill in the blanks:

Question 10. 1, 4, 9, 16. nth term is ……..

Answer. \(\mathrm{n}^2\)

Question 11. The cost of one book is 101 then the cost of p such books is ………

Answer. ₹ 101p