Haryana Board Class 8 Maths Algebra Chapter 2 Multiplication And Division Of Polynomials
Question 1. Multiply the following:
1. (4-5x) by (7x+6)
Solution:
Given (4-5x) by (7x+6)
(4-5x) by (7x+6) = (4-5x) (7x+6)
(4-5x) (7x+6) = 28x + 24 – 35x2 = 30x
(4-5x) (7x+6) = -35x2 = 2x+24
2. (a2-30+7) by (2a-5)
Solution:
Given (a2-3a+7) by (2a-5)
(a2-3a+7) by (2a-5) = (a2-3a+7) (2a-5)
(a2-3a+7) (2a-5) = \(2 a^3-6 a^2+14 a-5 a^2+15 a-35\)
(a2-3a+7) (2a-5) = \(2 a^3-11 a^2+29 a-35\)
Haryana Board Class 8 Maths Multiplication and Division of Polynomials Solutions
3. \(\left(x^2+x y+y^2\right) \text { by }\left(x^2-x y+y^2\right)\)
Solution:
Given \(\left(x^2+x y+y^2\right) \text { by }\left(x^2-x y+y^2\right)\)
= \(x^2\left(x^2+x y+y^2\right)-x y\left(x^2+x y+y^2\right)+y^2\left(x^2+x y+y^2\right)\)
= \(x^4+x^2 y+x^2 y^2-x x^y y-x^2 y^2-x y_3^3+x^2 y^2+x y_3^3+y^4\)
= \(x^4+x^2 y^2+y^4\)
4. \(\left(\frac{a^2}{b c}+\frac{b^2}{c a}\right) \text { by }\left(\frac{a}{b c}-\frac{b}{c a}\right)\)
Solution:
Given \(\left(\frac{a^2}{b c}+\frac{b^2}{c a}\right) \text { by }\left(\frac{a}{b c}-\frac{b}{c a}\right)\)
= \(\frac{a}{b c}\left(\frac{a^2}{b c}+\frac{b^2}{c a}\right)-\frac{b}{c a}\left(\frac{a^2}{b c}+\frac{b^2}{c a}\right)\)
= \(\frac{a^3}{b^2 c^2}+\frac{a b^2}{b c^2 a}-\frac{a^2 b}{a b c^2}-\frac{b^3}{a^2 c^2}\)
= \(\frac{a^3}{b^2 c^2}+\frac{b}{c^2}-\frac{a}{c^2}-\frac{b^3}{a^2 c^2}\)
Question 2. Find the Successive product of the following:
1. \((a+b),(a-b),\left(a^2-a b+b^2\right),\left(a^2+a b+b^2\right)\)
Solution:
Given \((a+b),(a-b),\left(a^2-a b+b^2\right),\left(a^2+a b+b^2\right)\)
= \(((a+b)(a-b))\left(\left(a^2-a b+b^2\right)\left(a^2+a b+b^2\right)\right)\)
= \(\left(a^2-a b+a b b-b^2\right)\left(a^4+a^3 b+a^2 b^2-a^3 b-a^2 b^2-a b^3+a^2 b^2+ab^3+b^4)\right.\)
= \(\left(a^2-b^2\right)\left(a^4+b^4\right)\)
= \(\left(a^2-b^2\right)\left(a^4-b^4\right)\)
= \(\left(a^6-b^6\right)\)
Class 8 Maths Chapter 2 Multiplication and Division of Polynomials Haryana Board
2. \(\left(a^2-b^2\right),\left(b^2-c^2\right),\left(c^2-a^2\right)\)
Solution:
Given \(\left(a^2-b^2\right),\left(b^2-c^2\right),\left(c^2-a^2\right)\)
= \(\left(\left(a^2-b^2\right)\left(b^2-c^2\right)\right)\left(c^2-a^2\right)\)
= \(\left(a^2 b^2-a^2 c^2-b^4+b^2 c^2\right)\left(c^2-a^2\right)\)
= \(c^2\left(a^2b^2-a^2 c^2-b^4+b^2 c^2\right)-a^2\left(a^2 b^2-a^2 c^2-b^4+b^2 c^2\right)\)
= \(\left(a^2 b^2 c^2-a^2 c^4-b^4 c^2+b^2 c^4-a^4 b^2+a^4 c^2+a^2 b^4-a^2 b^2 c^2\right)\)
= \(a^4 c^2-a^4 b^2-a^2 c^4-b^4 c^2+a^2 b^4+b^2 c^4\)
3. (x+1)(x-1)(x2 + 1)(x4 +1)
Solution:
Given: (x+1), (x−1), (x2 + 1), (x4+1)
= \(((x+1)(x-1))\left(\left(x^2+1\right)\left(x^4+1\right)\right)\)
= \(\left(x^2-x+x-1\right)\left(x^6+x^2+x^4+1\right)\)
= \(\left(x^2-1\right)\left(x^6+x^2+x^4+1\right)\)
= \(\left(x^2-1\right)\left(x^6+x^2+x^4+1\right)\)
= \(x^2\left(x^6+x^2+x^4+1\right)-1\left(x^6+x^2+x^4+1\right)\)
= \(x^8+x^4+x^8+x^4-x^6-x^2-x^4-1\)
= \(x^8-1\)
3. Simplify: (2x-3) (x+2)− (3x-5)(x-6) – (5+x)(7-x)
Solution:
Given: (2x-3)(x+2)-(3x-5) (x −6) − ( 5+x)(7-x)
(2x-3)(x+2)-(3x-5) (x −6) − ( 5+x)(7-x) = (2x2+4x-3x-6)-(3x2-18x-5x+30)-(35-5x+7x-x2)
(2x-3)(x+2)-(3x-5) (x −6) − ( 5+x)(7-x) = 2x2+x-6-3x2+23x-30-35-2x-x2
(2x-3)(x+2)-(3x-5) (x −6) − ( 5+x)(7-x) = 24x – 2x – 36 – 35 ⇒ 228-71
Question 4. If x= (a-b+c), y=(b-c+a) and 2 = (b+c-a) then find the value of (xy+yz+zx).
Solution:
Given x=(a+b+c), Y= (b-c+a), Z = (b+(-a)
xy+yz+Zx = ((a-b+c)(b-c+a)) + ((b-c+a) (b+c-a))+((b+c-a)(a-b+c))
xy+yz+Zx =(ab-ac + a2-b2 + bc-ab+cb-c2+ac) + (b2 + bc-ab-bc-c2+ac+ab+ac-a2)+(ab-b2+ bc+ac-bc+c2-a2+ab-ac)
xy+yz+Zx = a2– b2 +bc+cb-c2+b2-c2+ac+ac-a2+ab-b2+c2-a2+ab
xy+yz+Zx = 2ab+2bc+2ac-a2-b2-c2
Haryana Board 8th Class Maths Multiplication and Division of Polynomials Questions and Answers
Question 5. The area of a rectangle is (84x2-xy-15y2) Sq.cm and the length is (12x+5y) cm. Find the breadth of the rectangle.
Solution:
Length of a rectangle = 12x+5y
Breadth of a rectangle = B
Area of rectangle = 84x2-xy-15y2
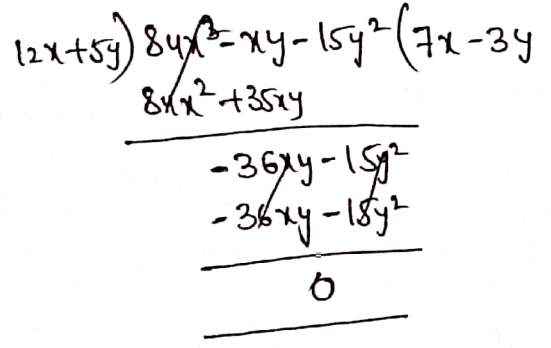
Breadth of a rectangle = 7x-3y
Question 6. The product of two numbers is (x3– 8) and one number is (x-2). Find the other number.
Solution:
Product of two numbers = x3-8
One number = (x-2)
Another number =?
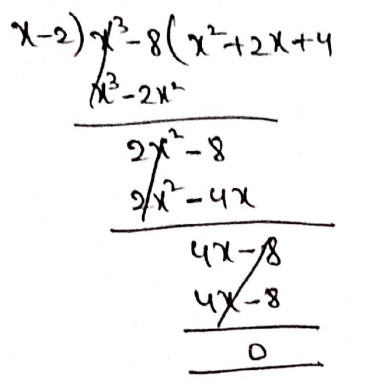
The product of another number = x2+2x+4
Question 7. Divide:
1. (x3 +17x-8x2-10) by (x-5)
Solution:
Given (x3+17x-8x2-10) by (x-5)
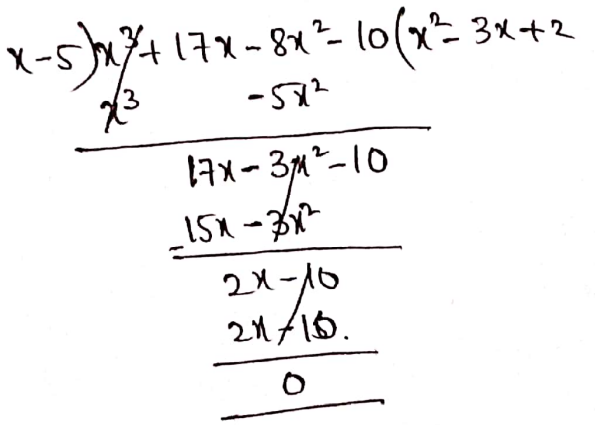
∴ (x2 – 3x+2)(x-5) = x3 +17x – 8x2-10
Chapter 2 Multiplication and Division of Polynomials Class 8 Solutions in Hindi Haryana Board
2. (x3-3x2y + 3xy2-y3) by (x-y)
Solution:
Given: (x3-3x2y + 3xy2-y3) by (x-y)
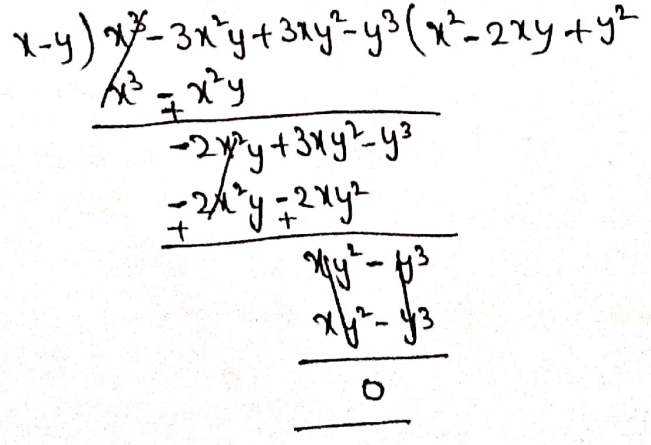
∴ (x2-2xy+y2)(x-y) = x3-3x2y+3xy2-y3
3. (a2/3+a1/3b1/3+b2/3) by (a-b)
Solution:
Given: (a2/3+a1/3b1/3+b2/3) by (a-b)
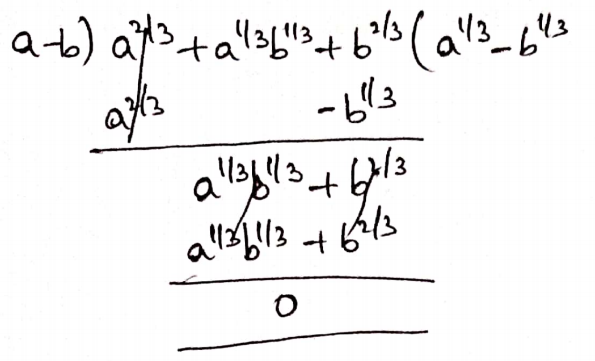
(a2/3+a1/3b1/3+b2/3) = (a-b)(a1/3– b1/3)
4. (5x – x2 – 6) by (12x3 – 66 + 97x – x4– 52x2)
Solution:
Given: (5x – x2 – 6) by (12x3 – 66 + 97x – x4– 52x2)
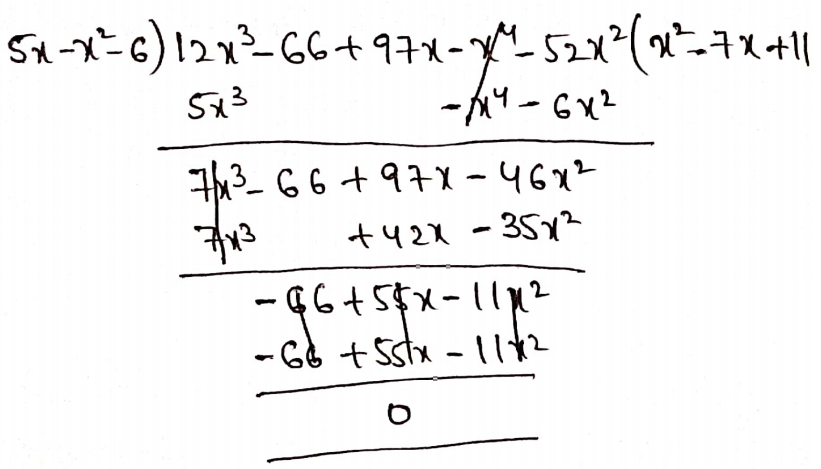
Question 8. Find the quotient and the remainder:
1. (x2-12x+30) by (x-5)
Solution:
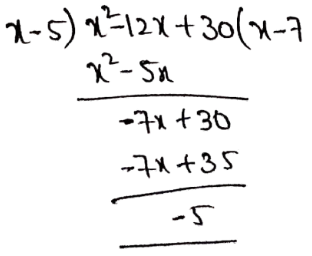
Quotient = (x-7)
Remainder = -5
Haryana Board Class 8 Maths Exercise 2.1 Solutions
2. (x2-3x+8) by (x4+2x3-14x2+63x-57)
Solution:
Given: (x4+2x3-14x2+63x-57) by (x2-3x+8)
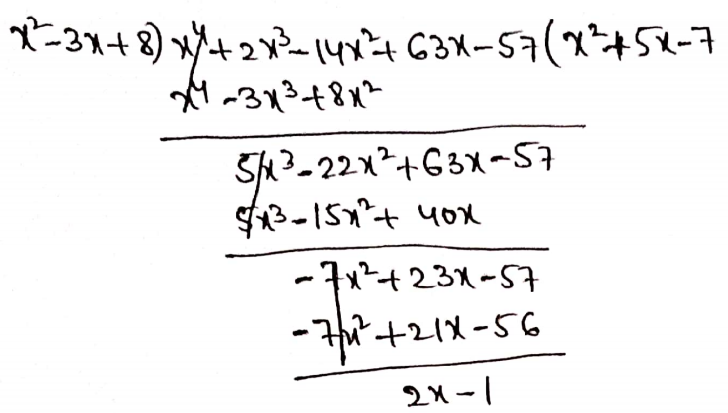
Quotient = (x2+5x-7)
Remainder = (2x-1)
3. (a3-2a2b+3ab2-5b3) by (a-2b)
Solution:
Given: (a3-2a2b+3ab2-53) by (a-2b)
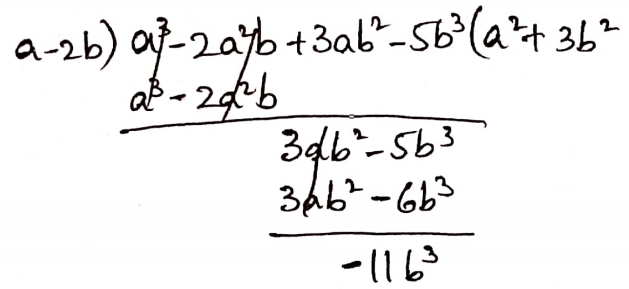
Quotient = (a2+3b2)
Remainder = -113
4. (x4+x2y2+2y4) by (x2+xy+y2)
Solution:
Given: (x4+x2y2+2y4) by (x2+xy+y2)
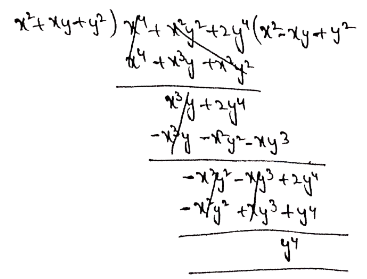
Quotient = (x2-xy + y2)
Remainder = y4
Important Questions for Class 8 Maths Chapter 2 Haryana Board
Question 9. Choose the correct answer:
1. (a+3) (a+4) (a+5)= _____________
- a3+12a2+47a+60
- a2+47a2+12a+60
- a3+12a2 +60a+47
- None of these
Solution: (a+3) (a+y) (a+5)
= (a2+4a+3a+12) (a+5) = (a2+7a+12)(a+5) = a3+35a+60+7a2+12a+5a2
= a3+12a2+47a+60
So, the Correct answer is (1)
2. (x4+2x2-x3+3+x) ÷ (x2+x+ 1) = _________
- x2=2x+3
- x2+2x-3
- x2+2x+3
- x2=2x-3
Solution:
So, the Correct answer is (1).
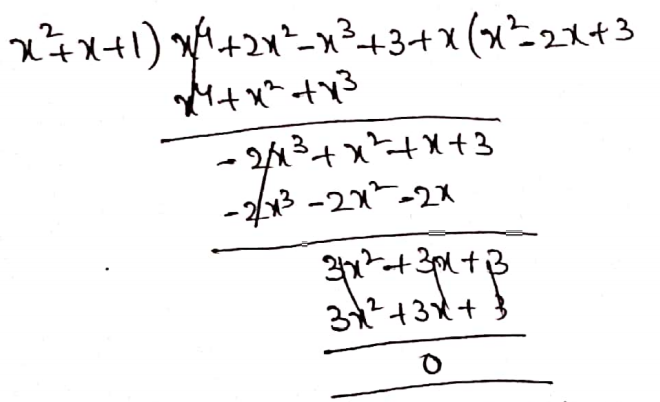
3. (8x8-8x2=-36x)÷ 4x = ____________
- 2x8-2x2-9
- 2x8-8x-36
- 2x7-2x-9
- 2x7-2x-18
Solution:
∴ \(\frac{8 x^8-8 x^2-36 x}{4 x}=2 x^7-2 x-9\)
The Correct answer is (3).
Step-by-Step Solutions for Multiplication and Division of Polynomials Class 8 Haryana Board
Question 10. write ‘True’ or ‘False”:
1. (x2+xy+y2) (x2-xy+y2) = x4+x2y2+y4
Solution:
(x2+xy+y2) (x2-xy+y2) = x4– x3y + x2y2 + x3y – x2y2 + xy3 + x2y2 – xy2 + y4
= x4 + x2y2 + y4
So, the statement is true.
2. (x2+7x+7) ÷ (x+3) = (x+4) – \(\frac{5}{x+3}\)
Solution:
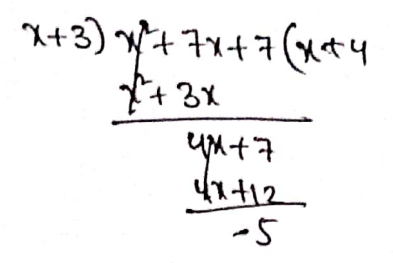
∴ \(\left(x^2+7 x+7\right) \div(x+3)=(x+4)-\frac{5}{x+3}\)
So the statement is true.
Question 11. Fill in the blanks:
1. (2x3-5x2-9x-8)=(x-4) = ______.
Solution:
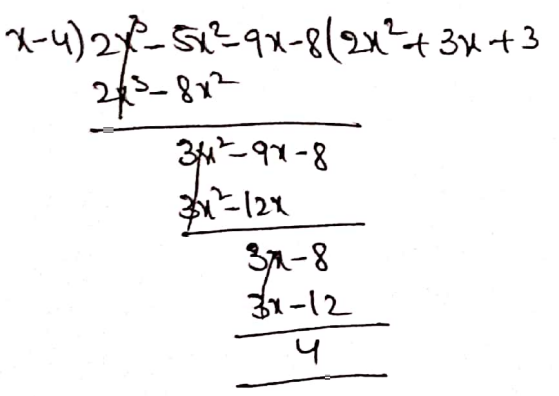
∴ \(\left(2 x^3-5 x^2-9 x-8\right) \div(x-4)=2 x^2+3 x+3+\frac{4}{x-4}\)
2. -3r2t(4+r45+2rt3) = __________
Solution:
∴ -3r2t(4+r4t5+2r3) = -12r6t6-6r3t4
3. (x2+xy+y2)(x-4)= __________
Solution:
(x2+xy+y2) (x-y)
(x2+xy+y2) (x-y) = x2(x-y)+xy(x-y) + y2 (x-y)
(x2+xy+y2) (x-y) = x3-x2y+x2y-xy2+xy2-y3
(x2+xy+y2) (x-y) = x3-y3
