Haryana Board Class 8 Maths Geometry Solutions For Chapter 3 Concept of Vertically Opposite Angles

Haryana Board Class 8 Maths Geometry Chapter 3  Concept of Vertically Opposite Angles

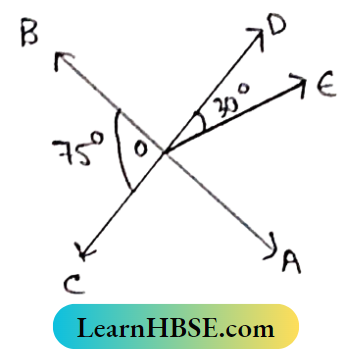
Question 1. In the adjacent figure find the measurement of ∠AOE, ∠BOD, and ∠AOC.

Solution:

∠AOD = ∠BOC (vertically opposite angles)

∠AOD = 90°

i.e., ∠AOE + ∠DOE = 75°

⇒ ∠AOE = 75-30 = 45°

Again, ∠BOD + ∠BOC = 180° (AS BO stands on CD)

∠BOD + 75° = 180°

⇒ ∠BOD = 180°- 75° = 105°

∠AOC = ∠BOD (Vertically opposite angles) = 105°

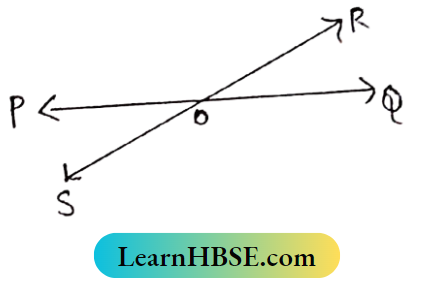
Question 2. In the adjoining figure if ∠POR=2 ∠QOR, then find the value of ∠POS.

Solution:

∠PQR + ∠QOR = 180° (AS OR Stands on PQ]

2∠QOR + ∠QOR = 180°

⇒ 3∠QOR = 180°

⇒ \(\angle Q O R=\frac{180^{\circ}}{3}=60^{\circ}\)

∠POS = ∠QOR (vertically opposite angles) = 60°

Class 8 Maths Chapter 3 Vertically Opposite Angles Haryana Board

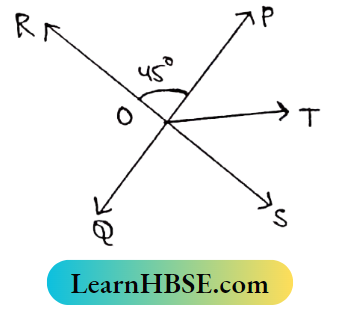
Question 3. Two Straight lines ∠PQ and ∠RS intersect at point O; OT is the bisector of ∠POS. If POR = 45°, then find ∠TOS.

Solution:

∠OP Stands On ∠RS.

∴ ∠POR + ∠POS = 180°

⇒ 45° + ∠POS = 180°

⇒∠POS= 180 °-45°= 135°

OT is the bisector of ∠POS

∴ ∠TOS = \(\frac{1}{2} \angle P O S=\frac{1}{2} \times 135^{\circ}=67 \frac{1}{2}^{\circ}\)

Haryana Board Class 8 Maths Vertically Opposite Angles Solutions

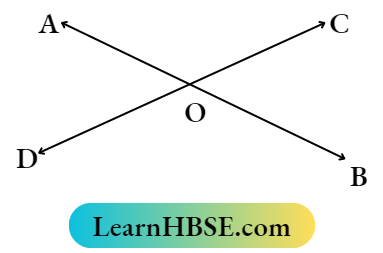
Question 4. If two straight lines intersect each other then four angles are formed. Find the Sum of the measurement of four angles.

Solution:

Let two straight lines AB and CD intersed at point O.

CO Stands on AB.

∴ ∠ADC + ∠COB = 180°

OD is stands on AB.

∴ ∠AOD + ∠BOD = 180°

∴ ∠AOC+ ∠COB + ∠AOD + ∠BOD = 130°+ 180°= 360°.

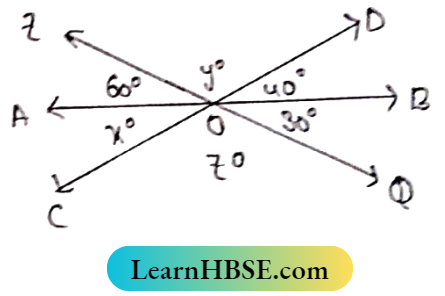
Question 5. In the adjacent figure find the value of x, y, and z?

Solution:

∠AOC = ∠BOD (vertically opposite angles)= 40°

∠AOP + ∠OOD + ∠BOD = 180°

60°+ y° + 48 = 180°

⇒ y° = 180°-100° = 80°

∠AOC + ∠COQ + ∠BOQ = 180°

40°+z°+30° = 180° ⇒ z° = 180°-70° = 110°

Haryana Board 8th Class Maths Vertically Opposite Angles Questions and Answers

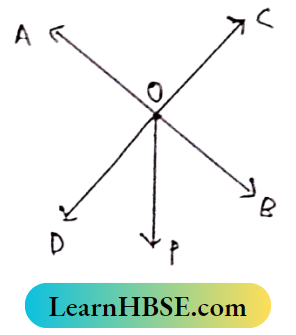
Question 6. The straight lines AB and CD intersect at point O; ∠AOD + ∠BOC = 102°, If Op is the bisector of ∠BOD, then find the measurement of ∠BOP.

Solution:

∠AOD = ∠BOC [vertically opposite angles)

∠AOD + ∠BOC = 102°

∠AOD + ∠AOD = 120°

⇒ 2∠AOD = 102°

⇒ ∠AOD = \(\frac{102^{\circ}}{2}=57^{\circ}\)

OD stands on AB

∴ ∠AOD + ∠BOD = 180°

51°+ ∠BOD = 180°

⇒ ∠BOD = 180°-51° = 129°

Op is the bisector of ∠BOD

∴ \(\angle B O P=\frac{1}{2} \angle B O D=\frac{1}{2} \times 129^{\circ}=64 \frac{1}{2}^{\circ}\)

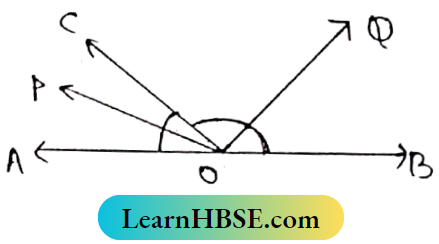
Question 7. Prove that internal and external bisectors of an angle are perpendicular to each other.

Solution:

Let op and OQ be the internal and external bisectors of ∠AOC respectively.

Required to prove: Op and OQ are perpendicular to each other.

Proof: OQ Is the external bisector of ∠AOC,

So OQ is the bisector of BOC.

∠POQ = ∠POC + ∠COQ

= \(\frac{1}{2}\) ∠AOC + \(\frac{1}{2}\) ∠COB

= \(\frac{1}{2}\) (∠AOC+ ∠COB) = \(\frac{1}{2}\) x ∠AOB

= \(\frac{1}{2}\) x 180° (one straight angle] = 90°

OP and OQ are perpendicular to each other.

Chapter 3 Vertically Opposite Angles Class 8 Solutions in Hindi Haryana Board

Question 8. PQ and RS are two straight lines intersecting at a point O. Prove that if the bisector of the LPOR is produced through O, it will bisect the ∠SOQ.

Solution:

Let AO is the bisect LPOR and let it be Produced to B.

Required to prove: OB bisects SOQ.

Proof: ∠SOB = ∠AOR [vertically opposite angles]

∠BOQ = ∠AOP [vertically opposite angles]

Again, ∠AOR = ∠AOP [AO is the bisector of POR]

∴ ∠SOB = ∠BOQ

∴OB bisects ∠SOQ (Proved).

Question 9. Choose the Correct answer:

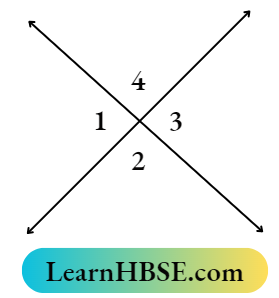
1. In the adjacent figure if ∠1 = 35°, then find the value of ∠2 is

1. 35°
2. 145°
3. 70°
4. 55°

Solution:

∠1 + ∠2 = 180°

35 + ∠2 = 180°

⇒ ∠2 = 180°-35° = 145°

So the Correct answer is (1).

Haryana Board Class 8 Maths Exercise 3.1 Solutions

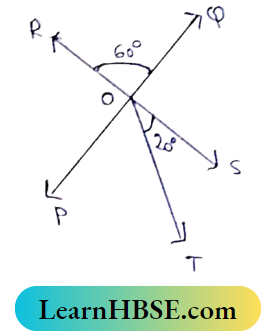
2. In the adjacent figure, if ∠TOS =20° and ∠ROQ = 60°, then the Value of ∠POT is

1. 66°
2. 120°
3. 40°
4. 80°

Solution:

∠POS = ∠ROQ (vertically opposite angles)

= 60°

i.e., ∠POT+∠TOS = 60°

⇒∠POT+20° = 60°

⇒∠POT = 60°-20° = 40°

So the Correct answer is (3)

Step-by-Step Solutions for Vertically Opposite Angles Class 8 Haryana Board

3. In the adjacent figure if ∠AOC + ∠BOP = 112°, the value of ∠BOC is

1. 112°
2. 56°
3. 68°
4. 124°

Solution:

∠AOC = ∠BOD

∠AOC+ ∠BOD = 112°

∠AOC + ∠AOC = 112°

⇒ 2∠A0C = 112°

⇒ ∠AOC = \(\frac{112^{\circ}}{2}=56^{\circ}\)

∴ ∠BOC + ∠AOC = 180°

⇒ ∠BOC = 180°-56° = 124°

So the Correct answer is (4)

Question 10. Write ‘True’ or ‘False”

1. The vertically opposite angle of 68° is 112°

Solution:

The vertically opposite angle of 68° is 68°

So the statement is false.

Important Questions for Class 8 Maths Chapter 3 Haryana Board

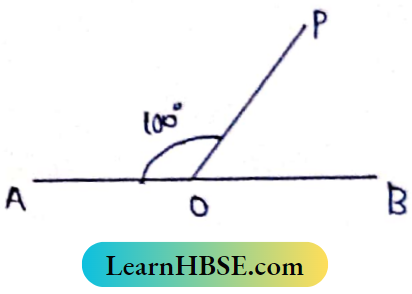
2. If op stands on line AB and ∠AOP = 100°, then the value of ∠BOP is 80°.

Solution:

OP is standing on AB

∴ ∠AOP + ∠BOP = 180°

∠AOP + 80° = 180°

⇒ ∠AOP = 180°-80° = 100°

So the Statement is true.

Question 11. Fill in the blanks:

1. If a ray Stands on a Straight line, then the Sum of measurement of two ________ angles so formed is 180°.

Solution: Adjacent.

2. The value of right angle is half of _________.

Solution: Straight angle.