Haryana Board Class 8 Maths Geometry Chapter 4 Properties Of Parallel Lines And Their Transversal
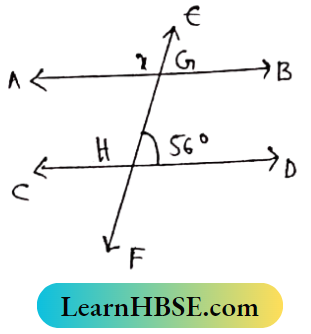
Question 1. In the adjacent figure find the Value of x.
Solution:
AB||CD and EF is transversal
∠EGB = ∠GHD (corresponding angles] = 56°
∠AGE + ∠EGB = 180° [AS GE stands on AB)
x + 56°= 180°
⇒ x = 180 ° – 56°
⇒ x = 124°
Properties of Parallel Lines and Their Transversal Worksheet Class 8
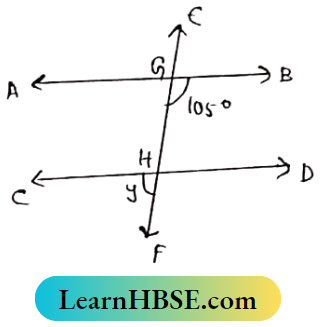
Question 2. In the adjacent figure find the value of y.
Solution:
AB||CP and EF are transversal.
∠DHF = ∠BGH. (Corresponding angles] = 105°
∠CHF = ∠DHF = 180°
y + 105° = 180°
⇒ y = 180°-105°
⇒ y = 75°
Haryana Board Class 8 Maths Geometry Chapter 4 Solutions
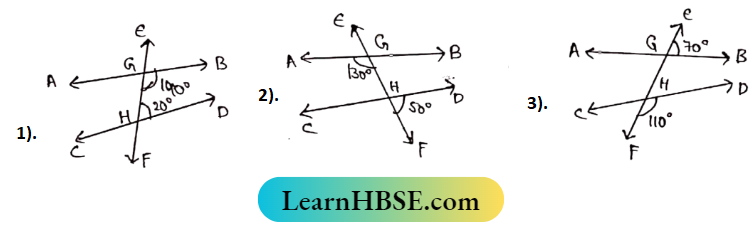
Question 3. Examine the measurement of the angles given below Concludes logically that AB and CD are parallel.
Solution:
1. ∠BGH + ∠GHD = 140°+ 20° = 160° ≠ 180 °
∴ AB and CD are not parallel lines to each other.
2. ∠BGH = 180°- ∠AGH
= 180°- 130°
= 50°
Again, ∠DHF = 50°
∠BGH = ∠DHF and these angles are Corresponding angles.
∴ AB||CD
3. ∠BGH = 180° – ∠EGB = 180°-70°
= 110°
Again, ∠DHF = 110°
∴ ∠BGH = ∠DHF and these angles are Corresponding angles.
∴ AB||CD.
Question 4. In parallelogram PQRS, if ∠P=90°, then find the values of the other three angles.
Solution:
In parallelogram PQRS,
SP||RQ and PQ is transversal.
∴ ∠P + ∠Q = 180°
∴ 90° + ∠Q= 180°
⇒ ∠Q = 180°-90°
= 90°
Again, SR||PQ and RQ are transversal.

Properties of Parallel Lines and Their Transversal Class 8 Solutions
Question 5. If the adjacent figure is PQ||RS; if ∠BAQ = 3∠ABS, then find the value of ∠RBN.
Solution:
AB||RS and MN is transversal.
∴ ∠BAQ + ∠ABS = 180°
3∠ABS + ∠ABS = 180°
⇒ 4∠ABS = 180°
⇒ ∠ABS = \(\frac{180^{\circ}}{4}=45^{\circ}\)
∠RBN = ∠ABS = 45°
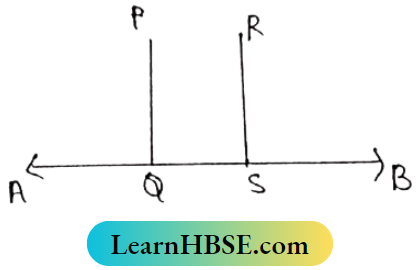
Question 6. Prove that Straight lines perpendicular to the Same straight line are parallel to one another.
Solution:
let PQ and Rs are both perpendicular to AB.
Required to prove: PQ||RS
Proof: PQ⊥AB
∴ ∠PQB = 90°
∴ RS⊥AB
∴ ∠RSB = 90°
∴ ∠PQB = ∠RSB and these are Corresponding angles.
∴ PQ||RS (Proved).
Parallel Lines and Transversals Class 8 Haryana Board Questions
Question 7. In the adjacend figure AB||CD, ∠RCD = 30°, ∠PAB = 50°, ∠PAC= 140°. Find the measurement of all the angles of ΔAQC.
Solution:
I drew Qs through Q which is parallel to AB.
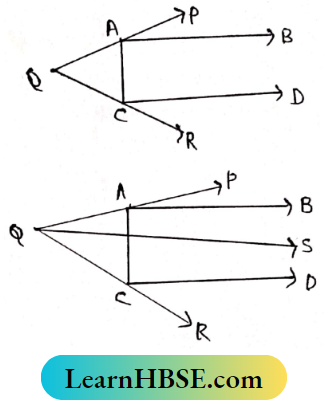
As AB||CD and AB||QS
∴ AB||QS||CP
AB||QS and PQ is transversal.
∴ ∠PQS = ∠PAB [Conrresponding angles) = 50°
QS||CD and QR is transversal.
∴ ∠RQS = ∠RCD (Corresponding angles) = 30°
∠AQC = ∠PQS +∠ RQS = 50°+30° = 80°
∠QAC + ∠PAC = 180°
∠QAC+ 140° = 180°
⇒ ∠QAC = 180°-140° = 40°
In ∠AQC, ∠AQC = 80°, ∠QAC = 40°
∴ ∠ACQ = 180°- (80°+40°) [In ΔAQC, ∠QAC+ ∠AQC + ∠ACQ = 180°)
= 180°-120° = 60°
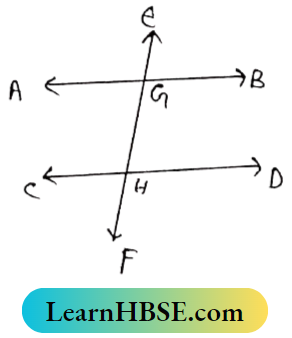
Question 8. In the adjacent figure, AB||CD and ∠EGB = 50% Find the Values of ∠AGE, ∠AGH, ∠CHF, and ∠DHF.
Solution.
∠AGE +∠ EGB = 180°
∠AGE +50° = 180°
∠AGE = 180°- 50° = 130°
∠AGH = ∠EGB [vertically opposite angles) = 50°
AB||CD and EF are transversal.
∴ ∠GHD = ∠AGH (Altemate angles] = 50°
∠CHF = ∠GHD = 50°
∠CHF + ∠OHF = 180°
50° + ∠DHF = 180°
∠DHF = 180°-50° = 130°
Class 8 Maths Chapter 4 Haryana Board Important Questions
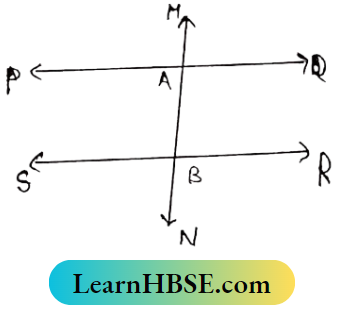
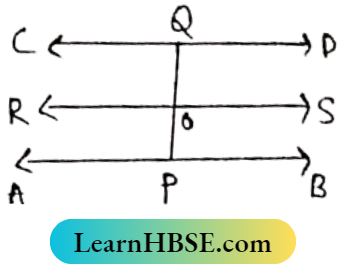
Question 9. O is any point inside two parallel lines AB and CD. Op and OQ are two perpendiculars on AB and CD respectively. prove that P, O, and Q are Collinear.
Solution:
Through O the straight line RS is drawn parallel to AB.
AB||CD and AB||RS.
∴ AB||CD||RS
OP⊥AB ∴∠OPB = 90°
OQ⊥CD ∴ ∠OQD = 90°
AB||RS and op is transversal.
∴ ∠OPB + ∠POS = 180°
90°+ Pos = 180°
⇒ ∠POS = 180°-90° = 90°
CD||RS and OQ are transversal.
∠OQD + ∠QOS = 180°
90°+ ∠QOS = 180°
⇒ ∠QOS = 180°- 90° = 90°
∠POQ = ∠QOS + ∠POS = 90° + 90° = 180°
∴ OP and OQ lie on the Same Straight line.
∴ P, O, and Q are collinear.
Question 10. If the Sides of angles are respectively parallel to the Sides of another angle, then the angles are either equal or Supplementary.
Solution:
Given: Let in angles ABC and ∠DEF, AB||DE and BC||EF, BC and DE intersect at G.
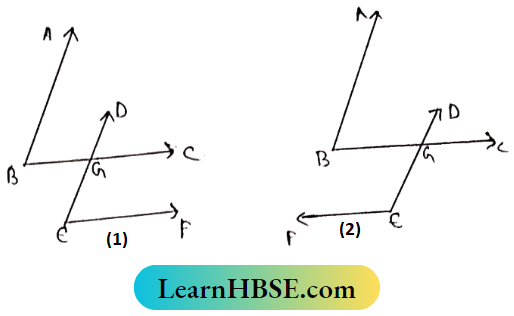
Required to prove:
1. ∠ABC = ∠DCF
2. ∠ABC and ∠DEF Supplementary i.e., ∠ABC + ∠DEF = 180°
Proof:
From (1) AB||DE and BC are transversal.
∴ ∠ABC = ∠DGC (Corresponding angles)
Again, BC||EF and DE is transversal.
∴ ∠DGC = ∠DEF (Corresponding angles)
AS ∠ABC = ∠DGC and ∠DGC = ∠DEF
∴ ∠ABC = ∠DEF (Proved).
From (2) BC||EF and DE is transversal
∴ ∠DGB = ∠DEF (Corresponding angles)
Again, AB||DE and Bc is transversal.
∴ ∠ABC + ∠DGB = 180°
∴ ∠ABC + ∠DEF = 180°
∴ ∠ABC and ∠DEF are Supplementary angles.
Haryana Board 8th Class Maths Geometry Notes Chapter 4
Question 11. Choose the Correct answer:
1. In the adjacent figure. If AB||CD, then the value of x is,
- 68°
- 22°
- 112°
- 34°
Solution:
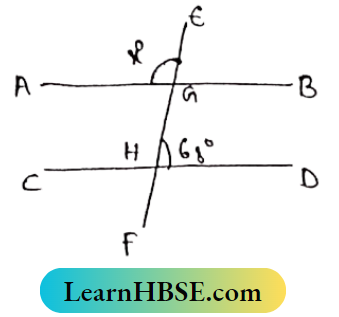
AB||CD and EF are transversal.
∴ ∠EGB = ∠GHD (Corresponding angles) = 68°
The ray GE is stands on line AB
∴ ∠AGE + ∠EGB = 180°
∠AGE + 63° = 180
⇒ ∠AGE = 180°- 68°-112° ⇒ x = 112°
So the Correct answer is (3).
Haryana Board Class 8 Chapter 4 Maths MCQ Questions
2. In the adjacent figure AB||CD, iF E∠GB = 50°, then the Value of x is
- 130°
- 40°
- 50°
- 60°
Solution:
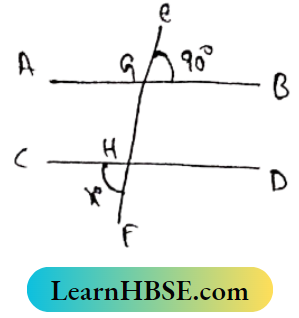
∠GHD = ∠EGB = 50°
∠CHF = ∠GHD (vertically opposite angle) = 50°
So the Correct answer is (3).
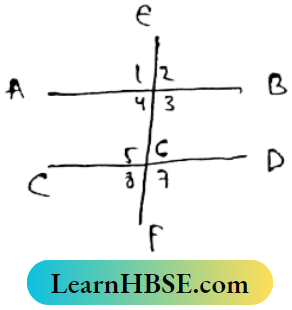
Question 12. Write ‘True’ or ‘False”:
1. In the adjacent figure if 3 = 120° and 8 = 60°, then AB||CD.
Solution:
∠6 + ∠8 = 60°
∠3 + ∠8= 120° + 60° = 180°
∴ AB||CD
So the Statement is true.
Class 8 Geometry Parallel Lines Theorem Explanation Haryana Board
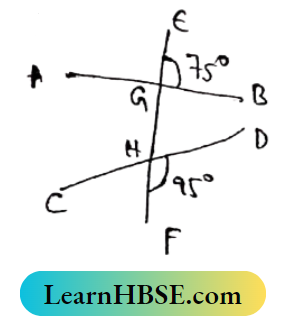
2. In the adjacent figure if ∠EGB = 75° and ∠PHF = 95°, then AB||CD
Solution:
∠AGH= ∠EGB (vertically opposite Angles) = 45°
∴ ∠GHC = ∠DHF = 95°
∠AGH + ∠GHC = 75°+95° = 170°
∴ AB and CD are not parallel to each other.
So the Statement is False.
Question 13. Fill in the blanks:
1. If a straight line intersects a pair of Straight lines and the measurement of one pair of Corresponding angles is equal, then the two straight lines are _______.
Solution: Parallel.
2. If the sides of an angle are respectively parallel to the sides of another angle, then the angles are either equal or _________.
Solution: Supplementary.
