Haryana Board Class 8 Maths Geometry Solutions For Chapter 6 Verification Of The Relation Between The Angles And Sides Of A Triangle

Haryana Board Class 8 Maths Geometry Chapter 6  Verification Of The Relation Between The Angles And Sides Of A Triangle

Question 1. In the adjacent figure, find the value of x.

Solution:

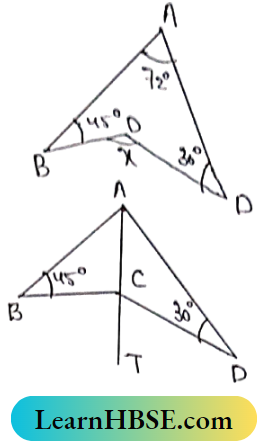
I joined A, C and AC is produced to T.

In ΔABC,

Exterior ∠BCT = ∠BAC + ∠ABC

In ΔACO,

Exterior ∠BCT = ∠BAC+ ∠ABC

In ΔACD,

Exterior ∠DCT = ∠DAC + ∠ADC

∠BCT + ∠DCT = (∠BAC+ ∠DAC) + ∠ABC + ∠APC

i.e ∠BCD = ∠BAD + ∠ABC + ∠ADC

x = 72°+45+30° ⇒ x = 147°.

Haryana Board Class 8 Maths Chapter 6 Solutions

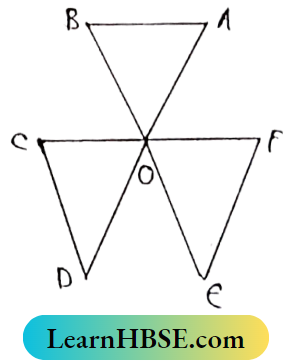
Question 2. In the adjacent figure find the Value of ∠A + ∠B + ∠C + ∠D + ∠E + ∠F.

Solution:

(∠A+∠B)+(∠C+∠D)+(∠E+∠F)

= ∠BOD + ∠DOF + ∠FOB = 360°

Question 3. In ABC, BC is produced to D. If ∠ACD = 126° and ∠B = \(\frac{3}{4}\) ∠A then find the Value of ∠A.

Solution:

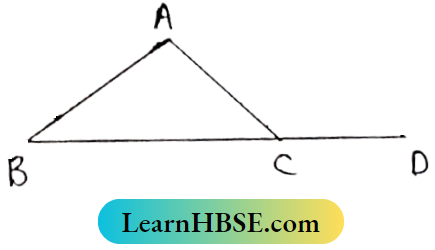
In ΔABC,

∠A + ∠B = exterior ∠ACD

⇒ \(\angle A+\frac{3}{4} \angle A=126^{\circ}\)

⇒ \(\frac{7 \angle A}{4}=126^{\circ}\)

⇒ \(\angle A=\frac{4}{7} \times 126^{\circ}\)

⇒ ∠A = 4 x 126°

⇒ ∠A = 4 x 18°

⇒ ∠A = 72°

Verification of the Relation Between Angles and Sides of a Triangle Class 8

Question 4. If O is an interior point of ABC, then find the relation between ∠BOC and ∠BAC.

Solution:

I join A, O and AD is extended to T

In ΔAOB, the exterior ∠BOT = ∠BAO + ∠ABO

∴ ∠BOT > ∠BAO

Similarly, In ΔAOC, ∠COT > ∠CAO

∴ ∠BOT + ∠COT > ∠BAO + ∠CAO

i.e., ∠BOC > ∠BAC. This is the relation.

Question 5. Find the Sum of measurement of all angles of a quadrilateral.

Solution:

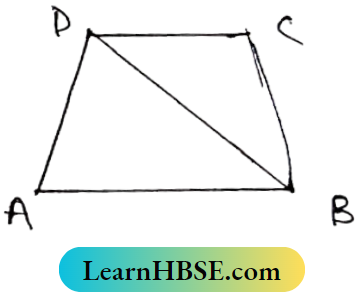
In quadrilateral ABCD, I join A,C.

In ΔABC,

∠BAC + ∠ABC + ∠ACB = 180°

In ΔADC, ∠DAC + ∠ADC + ∠ACD = 180°

(∠BAC + ∠DAC) + ∠ABC + ∠ADC + (∠ACB + ∠ACD) = 180° + 180°

∴ ∠BAD + ∠ABC+ ∠ADC + ∠BCD = 360°

Haryana Board Class 8 Maths Geometry Chapter 6

Question 6. In PQR, If ∠P = 80° and ∠Q= 70°, then find the relation between PQ and QR.

Solution:

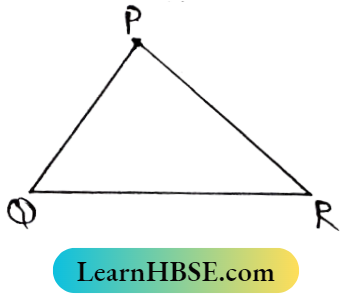
In ΔPQR, ∠P = 80°, ∠Q = 70°

∴ ∠R = 180°- (80°+70°) = 30°

As ∠P > ∠R ∴ QR >PQ (This the relation)

Question 7. The hypotenuse of a right-angled triangle is greatest One ____ Explain.

Solution:

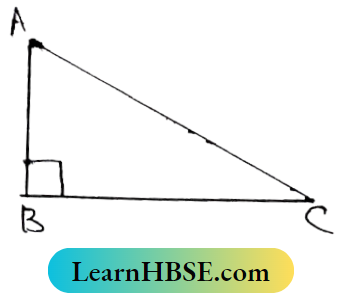
In ΔABC, ∠ABC = 90°

∴ Ac is the hypotenuse.

∠A and ∠C each are acute angles.

∴ ∠ABC > ∠A and ∠ABC > ∠C

As ∠ABC > ∠A ∴ ∠AC > ∠BC

As ∠ABC > ∠C ∴ AC > AB

∴ Ac is the largest side.

Triangle Angles and Sides Class 8 Haryana Board Questions

Question 8. If the ratio of measurement of angles of a triangle is 4:5:9; then write the nature of the triangle.

Solution:

Let the measurement of three angles are 4x°, 5x° and 9x°

4x°+5x°+9x° = 180°

⇒ 18x° = 180°

⇒ \(x^{\circ}=\frac{180^{\circ}}{18}=10^{\circ}\)

∴ The angles are 4×10° or 40°, 5×10° or 50° and 9×10° or 90°

∴ The triangle is a right-angled triangle.

Question 9. In ΔABC, the bisectors of ∠ABC and ∠ACB meet at 0. If AB > Ac then Prove that OB > OC.

Solution:

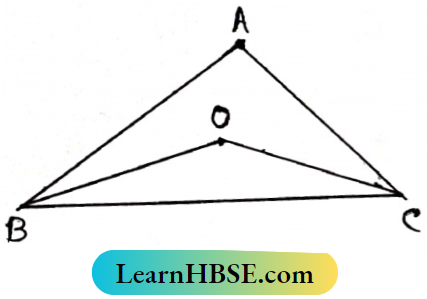
Given: In ΔABC, AB > AC, OB, and OC are the bisectors of ∠ABC and ∠ACB respectively.

RTP: OB > OC.

Proof: AB > AC

∴ ∠ACB > ∠ABC ⇒ ∠ACB > \(\frac{1}{2}\) ∠ABC

∴ ∠OCB > ∠OBC

∴ OB > OC (Proved).

Haryana Board Class 8 Maths Chapter 6 Important Questions

Question 10. In ΔPQR, the Internal bisector of ∠PQR and the external bisector of ∠PRQ intersect at T. If ∠QPR = 40° then find the Value of ∠QTR.

Solution:

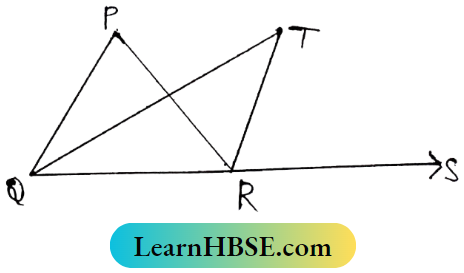
In ΔPQR,

⇒ ∠QTR + ∠TQR = exterior ∠TRS

⇒ ∠QTR = \(\frac{1}{2}\) ∠PRS = \(\frac{1}{2}\) ∠PQR

⇒ \(\frac{1}{2}\) (∠QPR + ∠PQR) – \(\frac{1}{2}\) ∠PQR

⇒ \(\frac{1}{2}\) ∠QPR + \(\frac{1}{2}\) ∠PQR – \(\frac{1}{2}\) ∠PQR

⇒ \(\frac{1}{2}\) ∠QPR = \(\frac{1}{2}\) x 40°

⇒ 20°

Class 8 Geometry Triangle Theorem Explanation Haryana Board

Question 11. Choose the Correct answer:

1. In ΔABC, AB = AC, BC is produced to D. If ∠ACD = 112°, then the Value of ∠BAC is

1. 44°
2. 68°
3. 22°
4. 34°

Solution:

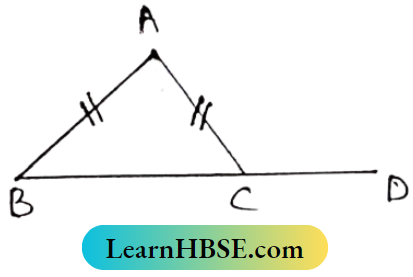
∠ACD + ∠ACB = 180°

112° + ∠ACB = 180°

Or, ∠ACB = 180°- 112° = 68°

In ΔABC, AB = AC, ∴ ΔABC = ∠ACB = 68°

In ΔABC, exterior ∠ACD = ∠BAC+ ∠ABC

112°= ∠BAC + 68°

⇒ ∠BAC = 112°-68° = 44°

So the Correct answer is (1).

2. In ΔABC, If ∠A =70° and ∠B=60°, then the relation between AB and BC is

1. AB = BC
2. AB > BC
3. AB < BC
4. None of these

Solution:

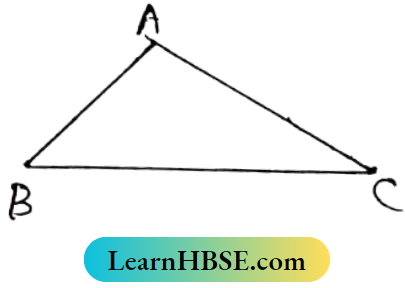
In ΔABC, ∠A + ∠B + ∠C = 180°

70° + 60° + ∠C = 180°

⇒ ∠C = 180° – 130° = 50°

As, ∠A > ∠C

∴ BC > AB ⇒ AB > BC

So the correct answer is (3).

Haryana Board Class 8 Maths Chapter 6 MCQ Questions

3. If the measurement of an angle of a triangle is equal to the Sum of the other two angles, then the triangle becomes.

1. Acute angled triangle
2. Obtuse angled triangle
3. Equilateral triangle
4. Right-angled triangle.

Solution:

In ΔABC, ∠A = ∠B + ∠C

∠A + ∠B + ∠C = 80°

∠A + ∠A = 180°

⇒ 2∠A = 180°

⇒ ∠A = 90°

The triangle is the right-angled triangle.

So the Correct answer is (4).

Question 12. Write ‘True’ or ‘False”.

1. If the ratio of measurements of the three angles of a triangle is 1:2:3, then the triangle becomes a right-angled triangle.

Solution:

Let the angles are x°, 2x°, and 3x°.

x+2x+3x = 180

⇒ 6x = 180

⇒ x = 30.

∴ The angles are 30°, 30°x2 or 6o° and 30°x3 or 90°

∴ The triangle is a right-angled triangle.

So the statement is true.

2. In the adjacent figure, if PQ || TS, then the Value of x is 80.

Solution:

∠QTS = ∠PQT [Alternate angle] = 55°

i.e., ∠RTS = 55°

In ΔRTS,

∠TRS + ∠RTS + ∠RST = 180°

x + 55° + 40° = 180°

⇒ x = 180° – 95° = 85°

So the statement is false.

Question 13. Fill in the blanks:

1. In an obtuse-angled triangle, the Opposite Side of __________ is the largest

Solution:

Let, In ΔABC, ∠B is an obtuse angle,

∴ ∠A and ∠C are both acute angles.

∴ ∠B > ∠A and ∠B > ∠C

As ∠B > A then AC > AB

∴ AC is largest

∴ The obtuse-angled triangle on the opposite side of the obtuse angle is the largest.

Relation Between Angles and Sides of a Triangle Class 8 Notes

2. In ΔABC, AB = AC; BC is produced to D. If ∠ACD = 105° then the value of ∠BAC is _________.

Solution:

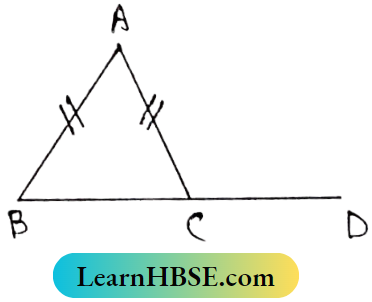
In, ∠ABC, ∠ACD = 105°

∠ACB = 180°- ∠ACD

= 180°-105° = 75°

AB = AC

∴ ∠ABC = ∠ACB = 75°

∠BAC + ∠ABC = Exterior ∠ACD

∠BAC + 75°= 105°

⇒ ∠BAC = 105° – 75°

= 30°