Haryana Board Class 8 Maths Solutions For Geometry Chapter 5 Relation Between Two Sides Of A Triangle And Their Opposite Angles

Haryana Board Class 8 Maths Geometry Chapter 5 Relation Between Two Sides Of A Triangle And Their Opposite Angles

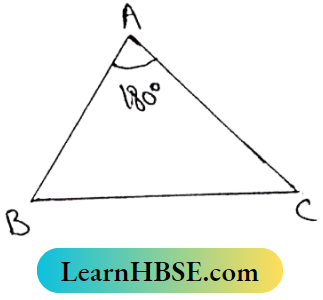
Question 1. If the measurement of the angle of an isosceles triangle is low, then find the measurement of the other two angles.

Solution:

The Sum of two acute angles is (180°-105°)

or 75°

Let ∠A = 105° and AB = AC

∴ \(\angle B=\angle C=\frac{180^{\circ}-105^{\circ}}{2}=\frac{75^{\circ}}{2}=37.5^{\circ}\)

Question 2. In an Isosceles triangle one angle of the base is 550, then find the measurement of the Vertical angle.

Solution:

In an isosceles triangle, one angle of the base is 55°.

The other angle of the base is 55°.

Then the vertical angle is 180°- (55°+ 55°) = 180°-110°= 70°

What is the relation between two sides of a triangle and their opposite angles?

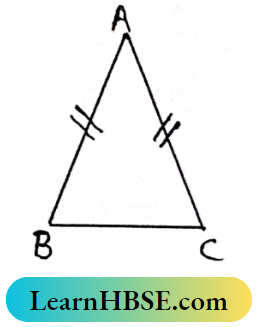
Question 3. In the adjacent figure, in ΔABC, AB = AC, If ∠A+∠B = 115°, find the measurement of ∠A.

Solution:

In ΔABE, ∠A + ∠B + ∠C = 180°

115° + ∠C = 180°

⇒ ∠C = 180° = 115°

⇒ ∠C = 65°

As AB = AC

∴ ∠B = ∠C = 65°

∠A = 115°-65° = 50°

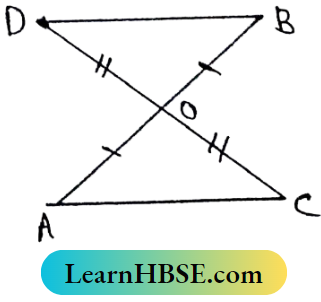
Question 4. Two line Segments AB and CD bisect each other at 0; If AC = 4cm, then find the length of BD.

Solution:

In ΔAOC and ΔBOD,

OA = OB, OC = OD

and ∠AOC = ∠BOD (vertically Opposite angle)

∴ ΔAOC ≅ ΔBOD (by AAS Congruency)

∴ Ac = BP

4cm = BD

∴ The length of BD is 40m.

How to prove the relation between sides and angles of a triangle in Class 8 Maths?

Question 5. In an isosceles triangle, the vertical angle is three times each angle of the base. Find the measurement of the Supplementary angle of the Vertical angle.

Solution:

Let the measurement of each angle of the base be x°

∴ The measurement of the vertical angle is 37°

The sum of the three angles of a triangle is 180°.

∴ 3x°+x°+x° = 180°

⇒ 5x°=180°

⇒ \(x^{\circ}=\frac{180^{\circ}}{5^{\circ}}=36^{\circ}\)

∴ The Vertical angle Is (3×36°) or 180°

The Supplementary angle of the Vertical angle is (180°-108°) Or 72°.

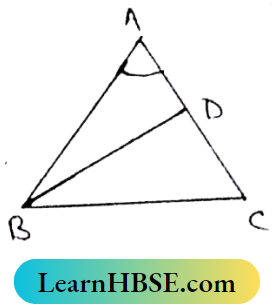
Question 6. In ΔABC, AB=AC, The bisector of ∠ABC intersects AC at D. If ∠A=56°, then find the Value of ∠ABD.

Solution:

In ΔABC,

AB = AC

∴ ∠ABC = ∠ACB

∠BAC=560

In ΔABC,

∠BAC + ∠ABC + ∠ACB = 180°

56° + ∠ABC + ∠ABC = 180°

⇒ 2 ∠ABC = 180°-56°=124°

⇒ \(\angle A B C=\frac{124^{\circ}}{2}=62^{\circ}\)

As BD is the bisector of ABC.

∴ \(\angle A B D=\frac{1}{2} \angle A B C=\frac{1}{2} \times 62^{\circ}=31^{\circ}\)

Question 7. In ΔABC, AB = AC; BC is extended to D Such that AC=CD; if ∠ABC=70°, then find the value of ∠BAD.

Solution:

In ABC, AB=AC

‍∴ ∠ACB = ∠ABC = 70°

Again, ∠ACB + ∠ACD = 180°

70° + ∠ACD = 180°

⇒ ∠ACD = 180°-70°

⇒ ∠ACD = 110°

In ΔACD, AC= CD ∴ ∠DAC = ∠ADC

∠ACD + ∠ADC + ∠DAC = 180°

110° + ∠ADC + ∠ADC = 180°

2∠ADC = 180°- 110° = 70°

⇒ \(\angle A D C=\frac{70^{\circ}}{2}=35^{\circ}\)

In ∠ABD + ∠ADB + ∠BAD = 180°

i.e., ∠ABC + ∠ADC+ ∠BAD = 180°

70°+35°+ BAD = 180°

⇒ ∠BAD = 180°-105° = 75°

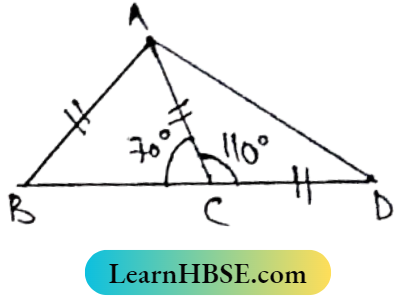
What is the theorem on the relation between sides and angles of a triangle?

Question 8. AB is the hypotenuse of the isosceles right-angled triangle ABC AD is the bisector of ∠BAC and AD intersects BC at D. Prove that AC + CD = AB.

Solution:

In the right-angled Isosceles triangle ABC, AB is the hypotenuse.

AD is the bisector of ∠BAC and AD Intersects BC at D.

Required to prove: Ac+CD = AB.

Construction: Through D I draw DC which is perpendicular to AB.

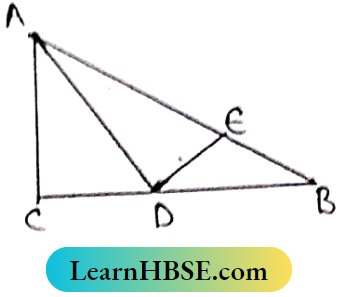
Proof: In ΔACD and ΔADE,

∠CAD = ∠EAD [as AD is the bisector of ∠BAC]

∠ACD = ∠AED = 90° [∵ DE ⊥ AB]

and AD is Common side.

∴ ΔACD ≅ ΔADE [by AAS Congruency)

∴ AC = AE [Corresponding Sides of Congwent triangles]

and CD = DE [Corresponding Sides]

In ΔABC, ∠ACB = 90° and AC = BC.

∴ ∠BAC = \(\angle A B C=\frac{90^{\circ}}{2}=45^{\circ}\)

In ΔBDE, ∠BED = 90°, B=45°

∴ ∠BDE = 180°-90° = 45° = 45°

∴ ∠BDE = ∠B ∴ BE = DE

Again CD = DE DE = CD = BE

AC+ CD = AE + BE = AB (Proved)

Question 9. Choose the Correct Answer:

1. In the adjacent figure, in ΔABC, which relation is correct?

1. AB = BC
2. AB = AC
3. AC = BC
4. AC ≠ BC

Solution:

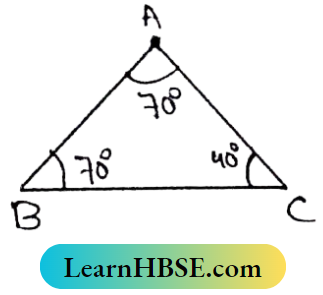
In ΔABC, ∠BAC = ∠ABC= 70°

∴ AC = BC (If the two angles of a triangle are equal then their opposite sides are equal)

So the Correct answer is (3).

What are the important theorems in Haryana Board Class 8 Maths Chapter 5?

2. In ΔABC, AB = AC; If ∠BAC = 70°, then the value of ∠ACB is

1. 70°
2. 110°
3. 35°
4. 55°

Solution:

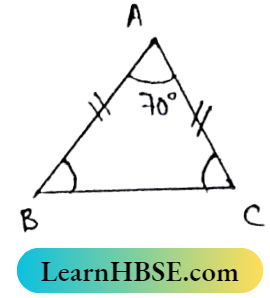
In ΔABC, AB = AC ∴ ∠ACB = ∠ABC.

Again, ∠BAC+ ∠ABC + ∠ACB = 180°

70° + ACB + ACB = 180°

⇒ 2∠ACB = 180°-70°

⇒ 2∠ACB = 110°

⇒ \(\angle A C B=\frac{110^{\circ}}{2}=55^{\circ}\)

So the correct answer is (4).

3. In the adjacent figure, in ΔABC, AB = AC and DE||BC; If ∠AED = 50°, then the value of ∠ABC is

1. 50°
2. 80°
3. 100°
4. 70°

Solution:

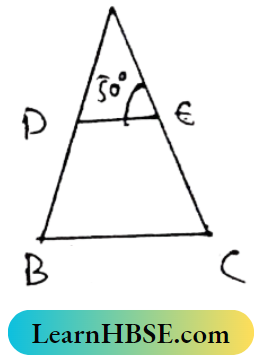
DE||BC and AC is transversal.

∴ ∠ACB = ∠AED (Corresponding angles) = 50°

In ΔABC, AB=AC ∴ ∠ACB = ∠ABC = 50° = ∠ABC.

So the correct answer is (1).

Question 10. Write ‘True’ and ‘False”.

1. The external bisector of the Vertical angle of an isosceles triangle is parallel to the base.

Solution: The Statement is true.

2. The Corresponding angles of two Congruent triangles are equal.

Solution: The statement is true.

How to solve Haryana Board Class 8 Geometry Chapter 5 problems step by step?

Question 11. Fill in the blanks:

1. The lengths of the hypotenuse of two _______ right-angled triangles are equal.

Solution: Congruent.

2. In an isosceles obtuse angle triangle the unequal angle is _________.

Solution: Obtuse angle