Important Questions for Class 11 Physics For Work and Energy

Question 1. An electron and a proton are detected In a cosmic ray experiment. Both of them have a kinetic 100 keV. Which one is faster?
Answer:

Given

An electron and a proton are detected In a cosmic ray experiment. Both of them have a kinetic 100 keV.

Kinetic energy, K = \(\frac{1}{2} m v^2 \text {, i.e., } v=\sqrt{\frac{2 K}{m}}\)

For the same kinetic energy, \(v \propto \frac{1}{\sqrt{m}}.\)

The mass of an electron is less than that of a proton.

So, the electron has a higher velocity, i.e., the electron is faster.

Important Questions For Class 11 Physics Work And Energy

Question 2. Is air resistance a conservative force?
Answer:

Air resistance is not a conservative force

To displace any object against air resistance, work has to be done. This work can never be restored, because to return the object to its initial state, further work has to be done to overcome the air resistance again. Hence air resistance is not a conservative force.

Question 3. A box Is lifted vertically by 6 m in 3 s.

1. If the box is lifted to the same height in a zig-zag way, or
2. If the box is lifted in 5 s instead of in 3s, what would be the change in the work done?

Answer:

1. Gravitational force is a conservative force. Hence, work done to lift a body to the same height will be the same, whatever may the nature of the path be.
2. Work done is independent of time. Hence, the same work is done in lifting the box in 5 s instead of in 3 s.

Applications Of Work And Energy Important Questions Class 11

Question 4. A hydrogen gas-filled balloon of mass m can rise to a maximum height of h above the earth’s surface. On the earth’s surface, the potential energy of the balloon = kinetic energy = 0; at the height h, the potential energy and kinetic energy of the balloon are mgh and 0 respectively. Is the law of conservation of energy violated here?
Answer:

Given

A hydrogen gas-filled balloon of mass m can rise to a maximum height of h above the earth’s surface. On the earth’s surface, the potential energy of the balloon = kinetic energy = 0; at the height h, the potential energy and kinetic energy of the balloon are mgh and 0 respectively.

The potential energy of an object of mass m raised the inclination. to a height h, is mgh. Here, mg = weight of the object = net downward force. But for a balloon of mass m, the net downward force is not mg.

When it is stationary at a height of h, the upward buoyancy balances the weight; the net downward force is zero. So the potential energy of the balloon at that height = 0, not mgh. This means that the total mechanical energy is zero, on the ground as well as at the height h. Thus, the law of conservation of energy is not violated.

Work And Energy Class 11 Important Questions With Answers

Question 5. What is the percentage increase in the momentum of a body when its kinetic energy increases by 69%?
Answer:

Kinetic energy, K = \(\frac{p^2}{2m}\), where p = momentum.

∴ \(\frac{K_1}{K_2}=\frac{p_1^2}{p_2^2} \quad \text { or, } \frac{p_2}{p_1}=\sqrt{\frac{K_2}{K_1}}=\sqrt{\frac{100+69}{100}}=\frac{13}{10}=\frac{130}{100}\)

∴ Increase in momentum = 30%.

Question 6. A particle of mass m, moving with a constant acceleration, acquires a velocity v₀ in time t₀. Initially, the particle was at rest. Find the average power and the instantaneous power of the applied force.
Answer:

Given

A particle of mass m, moving with a constant acceleration, acquires a velocity v₀ in time t₀. Initially, the particle was at rest.

Work done on the particle in time t₀ (W) = kinetic energy gained in \(t_0 s=\frac{1}{2} m v_0^2\)

Hence, average power, \(\frac{\frac{1}{2} m v_0^2}{t_0}=\frac{m v_0^2}{2 t_0}\)

If the velocity after a time t is v, then instantaneous power at a time t,

P = \(\frac{d W}{d t}=\frac{d}{d t}\left(\frac{1}{2} m v^2\right)=m v \frac{d v}{d t}=\frac{m v^2}{t}\)

(as for a constant acceleration \(\frac{d v}{d t}\) = \(\frac{v}{t}\))

Question 7. Is it possible to increase the kinetic energy of a body without applying an external force?
Answer:

The potential energy stored in a body can be transformed into its kinetic energy. Hence, it is possible to increase the kinetic energy of a body without applying an external force.

Class 11 Physics Work And Energy Numericals Important Questions

Question 8. The height of the vertex of an inclined plane is h. From the vertex, a body is released along the inclined plane. Explain whether the kinetic energy of the body at the base of the inclined plane depends on the inclination.
Answer:

Given

The height of the vertex of an inclined plane is h. From the vertex, a body is released along the inclined plane.

Let m = mass of the body.

Hence, the kinetic energy of the body at the base of the inclined plane = its potential energy at the vertex of the inclined plane = mgh.

Hence, the kinetic energy at the base depends on the height of the vertex h of the inclined plane, but not on the inclination.

Question 9. A body tied to a thread is made to revolve in a horizontal plane with a definite velocity and the thread does not snap. But when the body Is made to revolve in a vertical plane, the thread snaps. How is It possible?
Answer:

Given

A body tied to a thread is made to revolve in a horizontal plane with a definite velocity and the thread does not snap. But when the body Is made to revolve in a vertical plane, the thread snaps

Let the length of the thread be l, the mass of the body m, the velocity of revolution v, and tension in the thread T when the body is rotated in the horizontal plane.

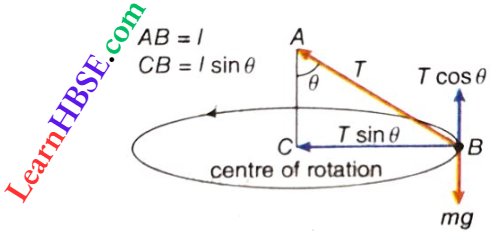
Required centripetal force for revolution, \(\frac{m v^2}{l \sin \theta}=T \sin \theta\)…(1)

and \(m g=T \cos \theta\)….(2)

From equations (1) and (2) we get, \(\sin ^2 \theta+\cos ^2 \theta=\frac{m v^2}{l T}+\left(\frac{m g}{T}\right)^2\)

or, \(T^2=\frac{m v^2}{l} T+m^2 g^2\)

or, \(T^2-\frac{m v^2}{l} T-m^2 g^2=0\)

∴ T = \(\frac{\frac{m v^2}{l} \pm \sqrt{\left(\frac{m v^2}{l}\right)^2+4 m^2 g^2}}{2}\)

∴ T>0 and \(\frac{m v^2}{l}<\sqrt{\left(\frac{m v^2}{l}\right)^2+4 m^2 g^2}\),

T = \(\frac{1}{2}\left[\frac{m v^2}{l}+\sqrt{\left(\frac{m v^2}{l}\right)^2+4 m^2 g^2}\right]\)

or, \(T=\frac{1}{2}\left[\frac{m v^2}{l}+\sqrt{\left(\frac{m v^2}{l}+2 m g\right)^2-2 \cdot \frac{m v^2}{l} \cdot 2 m g}\right]\)…(3)

Now, \(\frac{m v^2}{l}+2 m g>\sqrt{\left(\frac{m v^2}{l}+2 m g\right)^2-2 \cdot \frac{m v^2}{l} \cdot 2 m g}\)

∴ From equation (3), it can be inferred that

T< \(\frac{1}{2}\left[\frac{m v^2}{l}+\left(\frac{m v^2}{l}+2 m g\right)\right]\)

or, \(T<\left(\frac{m v^2}{l}+m g\right)\)….(4)

Again, when the body is revolved in the vertical plane, tension in the thread at the lowest point of the circular path,

T’ = \(\frac{m v^2}{l}+m g\)…(5)

From equations (4) and (5) we get, T < T’

So, the tension in the thread at the lowest point in the second case is greater than that in the first case, and hence, in the first case though the thread does not snap, in the second case the thread may snap.

Work And Energy Derivation Important Questions Class 11

Question 10. Two bodies of different masses have the same momentum. Compare their kinetic energies.
Answer:

Given

Two bodies of different masses have the same momentum.

Let K₁, P_1, and K₂, p₂ be the kinetic energies and momenta of the two bodies of masses m₁ and m₂, respectively.

Now, \(K=\frac{1}{2} m v^2=\frac{m^2 v^2}{2 m}=\frac{p^2}{2 m}\)

∴ \(K_1=\frac{p_1^2}{2 m_1}, K_2=\frac{p_2^2}{2 m_2}\)

∴ \(\frac{K_1}{K_2}=\frac{m_2 p_1^2}{m_1 p_2^2}=\frac{m_2}{m_1} \quad \text { as } p_1=p_2\)

Hence, the body with the lighter mass has greater kinetic energy, i.e., the kinetic energy is inversely proportional to the mass, if the momentum remains constant.

Question 11. An unbalanced system of forces can produce acceleration as well as deformation in a body, but ‘a balanced system of forces produces deformation only.
Answer:

Given

An unbalanced system of forces can produce acceleration as well as deformation in a body, but ‘a balanced system of forces produces deformation only.

In case of an unbalanced system of forces acting on a body, a resultant force acts at the center of mass. The body accelerates, as per the equation, F = ma. But for a balanced system of forces, the resultant force is zero and hence the acceleration of the centre of mass is zero.

However, in both situations, different parts of the body may have relative velocities with respect to one another. Hence, deformation may take place.

For example, if a rubber rope is pulled on both ends with equal forces, the rope extends in length, i.e., it is deformed, but its center of mass remains steady at one place. When the forces applied at the ends are unequal, the rope not only extends but also moves in the direction of the greater force.

Long Answer Questions On Work And Energy Class 11 Physics

Question 12. What are the characteristics of an elastic collision between two bodies?
Answer:

The characteristics of an elastic collision between two bodies

In an elastic collision,

1. Total kinetic energy is conserved and
2. Total momentum is conserved.

Question 13. Two protons are drawn near each other. Will the potential energy of the system increase or decrease? What will happen if a proton and an electron are drawn near each other?
Answer:

Given

Two protons are drawn near each other.

Since the protons are positively charged particles, they will repel each other. To bring them nearer, work has to be done against the force of repulsion and this will be stored up in the system as potential energy. So the potential energy of the system will increase. The potential energy decreases when a proton and an electron are brought nearer.

Question 14. What is the condition for the collision of two bodies to be one-dimensional?
Answer:

The speeds of the centers of mass of the two particles before the collision must be along the same straight line.

Work Energy Theorem Important Questions Class 11

Question 15. A shot is fired from a gun. What will be the changes in momentum and kinetic energy?
Answer:

Given

A shot is fired from a gun.

The momentum of the system will be conserved. However the kinetic energy will increase because the chemical energy of the explosives used in firing will be converted into kinetic energy.

Short Answer Questions On Work And Energy Class 11

Question 16. A molecule in a gas container hits a horizontal wall with a speed of 200 m · s^-1 at an angle of 30° with the normal and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?
Answer:

Given

A molecule in a gas container hits a horizontal wall with a speed of 200 m · s^-1 at an angle of 30° with the normal and rebounds with the same speed.

As there is no external force, linear momentum is conserved. The collision is elastic because the magnitude of the molecular velocity remains the same.