Overview Of Thermodynamic Cycles

First And Second Law Of Thermodynamics Carnot Cycle

According to the second law of thermodynamics, no heat engine can have 100% efficiency. In 1824 french scientist N.L Sadi Camot. developed a hypothetical, idealized heat engine that has the maximum efficiency (given two heat reservoirs at temperatures T₁ and T₂ consistent with the second law of thermodynamics. The cycle over which this engine operates is called the Camot cycle.

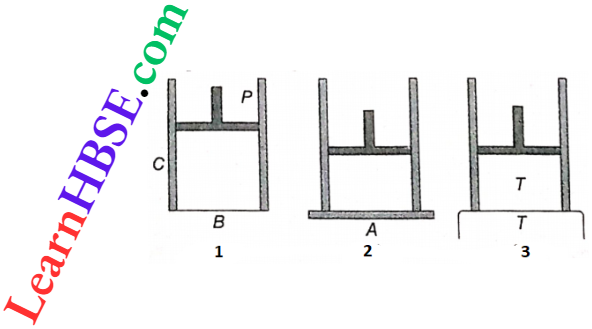
Standard cylinder piston Arrangement: C is a cylinder. The piston P is an airtight one, capable of sliding within C. This, expansions or contractions of a substance kept inside the cylinder may occur. B is the bottom surface of the cylinder through which an exchange of heat between the cylinder and the surroundings can take place.

• If a cylinder filled with some quantity of a gas is placed on plate A, the gas exchanges no heat with the surroundings through any wall.
• So upward or downward movement of the piston causes adiabatic expansion or adiabatic contraction, respectively.
• On the other hand, if the cylinder is placed on a heat reservoir at temperature T, the equilibrium temperature of the gas inside the cylinder also becomes T.
• Now, if the piston is moved upward or downward, the gas takes heat from or rejects heat to the heat reservoir, respectively, and all along the temperature of the gas remains at T.

In this way, isothermal expansion or isothermal contraction takes place. Of course, the piston is to move up and down very slowly, so that sufficient time is obtained for heat exchange between the cylinder and the heat reservoir.

Overview Of Thermodynamic Cycles

Description of a Carnot code on a pV-diagram: Two isothermal curves at temperatures T₁ and T₂ are shown on a pV-diagram. In addition, two adiabatic curves are also shown. The points of intersection of these four curves are a, b, c, d

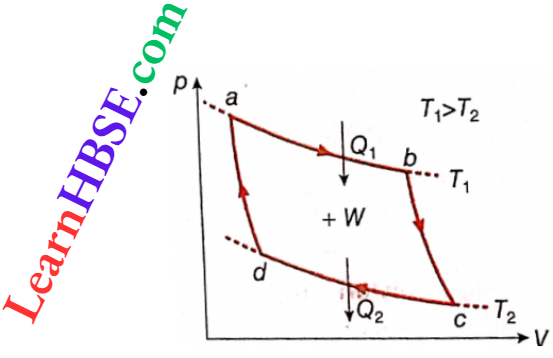
Initially, the system is taken in a cylinder fitted with a piston in such a way that it is in the state a. In this condition pressure, volume, and temperature of the gas are p_a, V_a, and T₁ respectively. Next, the following four reversible processes are performed on the system.

1. Reversible isothermal expansion a  → b: At the state b the properties of the gas are p_b, V_b, T₁. According to the figure, since V_b> V₄, it is an expansion. Since this expansion takes place along an isothermal curve, the temperature T₁ remains constant.

2. Reversible adiabatic expansion b → c: At the state c the properties of the gas are p_c, V_c, T₂. In this case also, since V_c > V_b, it is an expansion. Due to this expansion, the temperature comes down to T₂ from T₁.

3. Reversible isothermal contraction c → d: The point d is situated on the adiabatic curve through the point a. The properties of the gas at the state d are p_d, V_d, T₂.

4. Reversible adiabatic contraction d → a: Due to this contraction, the gas returns to its initial state a, i.e., a cycle becomes complete. This cycle is a Carnot cycle.

So, a cycle enclosed by four reversible processes, two isothermals and two adiabatics, is called a Carnot cycle.

Action of a Carnot cycle: The Carnot cycle shown is a clockwise cycle. So the work done due to this cycle is positive and the area abed of the cycle on the p-V diagram indicates this work (W).

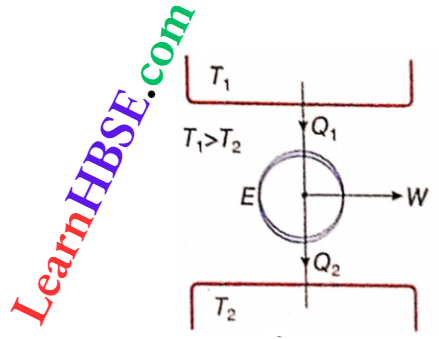
The two processes b → c and d → a are adiabatic, i.e., in these two processes, no heat exchange takes place with the surroundings. Again, the process a → b is an isothermal expansion. So the gas takes up heat Q₁ from the source at higher temperature T₁.

• On the other hand, the process c → d is an isothermal contraction. So an amount of heat Q₂ is rejected to the sink at lower temperature T₂.
• This action of the Carnot cycle can be expressed. Obviously, in a complete cycle, the Q₁ amount of heat is taken from the source at a higher temperature T₁. A part of this heat is converted into work W, and the remaining part Q₂ is rejected to the sink at lower temperature T₂.
• This means that this clockwise Carnot cycle acts as a heat engine. This is called a Carnot engine. Since each process of the cycle is reversible, the engine E is a reversible heat engine working between two temperatures.

Types Of Thermodynamic Cycles With Examples

Efficiency of a Carnot engine using an ideal gas: Suppose, n mol of an ideal gas is used as the working substance of the Carnot cycle. In this case, the temperature of the source = T₁ and the temperature of the sink = T₂: T₂ < T₁.

In isothermal expansion a → b,

heat taken, \(Q_1=n R T_1 \ln \frac{V_b}{V_a}\)…(1)

Again, in isothermal compression c →d,

heat rejected, \(-Q_2=n R T_2 \ln \frac{V_d}{V_c}\);

as \(Q_2\) is rejected heat, the negative sign is taken.

∴ \(Q_2=n R T_2 \ln \frac{V_c}{V_d}\)…(2)

So, the efficiency of the Carnot engine,

⇒ \(\eta=1-\frac{Q_2}{Q_1}=1-\frac{T_2}{T_1} \cdot \frac{\ln \left(\frac{V_c}{V_d}\right)}{\ln \left(\frac{V_b}{V_a}\right)}\)…(3)

Now, in case of an adiabatic process of an ideal gas, \(T V^{\gamma-1}=\text { constant }\)

where \(\gamma\) is the ratio of the two specific heats \(C_p and C_\nu\) of the gas.

So, for the adiabatic process b → c, \(T_1 V_b^{\gamma-1}=T_2 V_c^{\gamma-1}\)

or, \(\frac{T_1}{T_2}=\left(\frac{V_c}{V_b}\right)^{\gamma-1}\)…(4)

For the adiabatic process d → a, \(T_2 V_d^{\gamma-1}=T_1 V_a^{\gamma-1}\)

or, \(\frac{T_1}{T_2}=\left(\frac{V_d}{V_a}\right)^{\gamma-1}\)

Comparing equations (4) and (5) we have,

⇒ \(\frac{V_c}{V_b}=\frac{V_d}{V_a} \text { or, } \frac{V_c}{V_d}=\frac{V_b}{V_a}\)…(6)

So, from equations (1) and (2) we have, \(\frac{Q_1}{Q_2}=\frac{T_1}{T_2}\)…(7)

Again from equation (3), the efficiency of a Carnot engine

⇒ \(\eta=1-\frac{T_2}{T_1}\)…(8)

From this equation, it is evident that the efficiency of a Carnot engine depends only on the temperatures of the source and the sink. Again, η = 1 = 100% if T₂ = 0.

Since absolute zero is not attainable, a Carnot engine with 100% efficiency is a practical impossibility.

Thermodynamic Cycles Used In Power Plants

Use of other materials In a Carnot angina: it is not that only ideal gas is always used as a working substance in heat engines. Substances like a real gas, or a mixture of a liquid and vapor (for example, mixture of steam and water in a steam engine) are used in many cases as working substances.

Using the second law of thermodynamics, Carnot showed that

1. All reversible engines working between the same two temperatures have the same efficiency and
2. No engine working between two given temperatures can be more efficient than a reversible engine working between the same two temperatures.

This is Carnot’s theorem. Proof of this theorem is beyond our syllabus.

• Carnot engine is a reversible engine. Its efficiency between the temperatures T₁ and T₂ is \(\eta=1-\frac{T_2}{T_1}\), when the working substance is an ideal gas.
• According to Carnot’s theorem, it is not that this expression is only applicable to ideal gases. Whatever the working substance used in a Carnot engine may be, if it works between the same two temperatures, its efficiency will be the same.
• In general, a Carnot cycle can be performed with any thermodynamic system as a working substance example, hydrostatic, chemical, electrical, magnetic, or otherwise.

So die expression of the efficiency of the Carnot engine, i.e., equation (8) will be valid not only for ideal gases but also for any working substance.

Carnot refrigerator cycle: A clockwise Carnot cycle behaves as a heat engine. This is called a Carnot engine. If this Carnot cycle operates in an anticlockwise direction debt, then work done and the exchange of heat in the four reversible processes will be equal but opposite to the corresponding quantities of the Carnot engine. This means that the anticlockwise Carnot cycle will act as an arrangement such that in each cycle

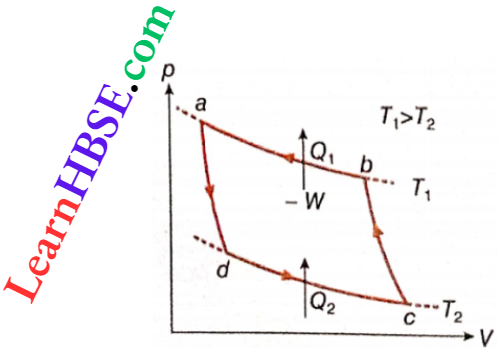
1. Some amount of heat Q₂ will be taken from lower temperature T₂.
2. Some amount of external work (W) is to be supplied
3. Some amount of heat Q₁ will be rejected to higher temperature T₁.

Thermodynamic Cycles In Refrigeration And Air Conditioning

It is obvious that the arrangement R shown acts as a refrigerator. In this case, the anticlockwise Carnot cycle bounded by two reversible isothermal processes and two reversible adiabatic processes is called a Carnot refrigerator.

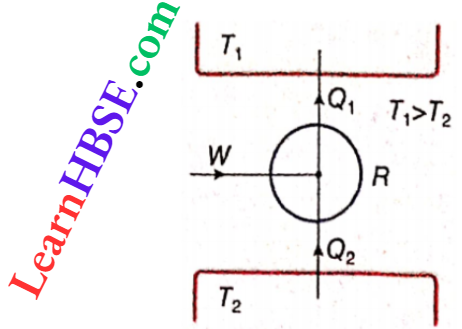
Interconversion between Carnot engines and refrigerators: Both Carnot engines and Carnot refrigerators are reversible. So it is possible to use Carnot engine as a Carnot refrigerator, and vice versa. For this, only the processes of a Carnot cycle should be reversed.

But no process is reversible in reality. All real processes are irreversible. So Carnot engine or Carnot refrigerator is only an ideal arrangement. They cannot be prepared practically. All practical engines or refrigerators are irreversible. These cannot be operated in reverse. So no heat engine can be converted into a refrigerator, and vice versa.

Coefficient of performance of a Canot refrigerator: The coefficient of performance of a Carnot refrigerator,

e = \(\frac{\text { output }}{\text { input }}=\frac{\text { heat taken from cold body }}{\text { work supplied from outside }}\)

= \(\frac{Q_2}{W}\) according to figures,

= \(\frac{Q_2}{Q_1-Q_2}=\frac{1}{\frac{Q_1-Q_2}{Q_2}}=\frac{1}{\frac{Q_1}{Q_2} e^1}\)

Now, in case of a Carnot refrigerator, work done and heat exchange are equal and opposite to the corresponding quantities of a Carnot engine. So, following the calculations for the determination of the efficiency of a Carnot engine, it is evident that in case of a Carnot refrigerator, \(\frac{Q_1}{Q_2}=\frac{T_1}{T_2}\)

Therefore, e = \(\frac{1}{\frac{T_1}{T_2}-1}=\frac{1}{\frac{T_1-T_2}{T_2}}=\frac{T_2}{T_1-T_2}\)

Thermodynamics

First And Second Law Of Thermodynamics Carnot Cycle Numerical Examples

Example 1. A Carnot engine is being operated by taking heat from a source at a temperature 527°C. If the surrounding temperature is 27°C, what is the efficiency of the engine? If the source supplies heat at the rate of 10⁹ J per minute, how much usable work is obtained per minute?
Solution:

Given

A Carnot engine is being operated by taking heat from a source at a temperature 527°C. If the surrounding temperature is 27°C

Temperature of the source, T₁ = 527°C = (527 + 273) K = 800 K

The temperature of the sink, T₂ = 27°C = (27 + 273) K = 300 K T.

So, efficiency \(\eta=1-\frac{T_2}{T_1}=1-\frac{300}{800}=\frac{5}{8}=\frac{5}{8} \times 100 \%=62.5 \%\)

Now, \(\eta=\frac{W}{Q_1}\)

∴ W = \(\eta Q_1=\frac{5}{8} \times 10^9=6.25 \times 10^8 \mathrm{~J} \cdot \mathrm{min}^{-1}\) .

Comparison Of Different Thermodynamic Cycles

Example 2. A Carnot engine takes up 200 cal of heat per cycle from a source at a temperature 500K and rejects 150 cal of heat to the sink. What is the temperature of the sink and the efficiency of the engine?
Solution:

Given

A Carnot engine takes up 200 cal of heat per cycle from a source at a temperature 500K and rejects 150 cal of heat to the sink.

⇒ \(\frac{Q_1}{Q_2}=\frac{T_1}{T_2} or, T_2=T_1 \cdot \frac{Q_2}{Q_1}=500 \times \frac{150}{200}=375 \mathrm{~K}\)

Efficiency, \(\eta=1-\frac{Q_2}{Q_1}\)

= \(1-\frac{T_2}{T_1}=1-\frac{375}{500}=1-\frac{3}{4}=\frac{1}{4}\)

= \(\frac{1}{4} \times 100 \%=25 \% .\)

Example 3. The temperatures of the source and the sink of a Carnot engine are 500 K and 300 K respectively. If the temperature of the source diminishes to 450 K, what will be the percentage change in efficiency?
Solution:

Given

The temperatures of the source and the sink of a Carnot engine are 500 K and 300 K respectively. If the temperature of the source diminishes to 450 K

In the first case, efficiency, \(\eta_1=1-\frac{T_2}{T_1}=1-\frac{300}{500}=\frac{2}{5}\)

In the second case, efficiency, \(\eta_2=1-\frac{T_2}{T_1}=1-\frac{300}{450}=\frac{1}{3}\)

∴ Fractional change in efficiency

= \(\frac{\eta_2-\eta_1}{\eta_1}=\frac{\eta_2}{\eta_1}-1=\frac{1 / 3}{2 / 5}-1=\frac{5}{6}-1=-\frac{1}{6}\)

∴ Percentage change = -1/6 x 100 = -16.67%

So, efficiency decreases by 16.67%.

Efficiency Of Thermodynamic Cycles

Example 4. The temperature of the ice box of a refrigerator is -7°C and the room temperature is 31°C. To maintain the temperature of the ice box, the refrigerator rejects 20000 cal of heat per minute. If the refrigerator approximates a Carnot refrigerator, what is its power consumption?
Solution:

Given

The temperature of the ice box of a refrigerator is -7°C and the room temperature is 31°C. To maintain the temperature of the ice box, the refrigerator rejects 20000 cal of heat per minute.

Temperature of the ice-box = (-7 + 273) K = 266 K

Temperature of the surrounding = (31 + 273)K = 304 K

∴ Coefficient of performance,

e = \(\frac{T_2}{T_1-T_2}=\frac{266}{304-266}=\frac{266}{38}=7\)

Again, e = \(\frac{Q_2}{W}\)

∴ W = \(\frac{Q_2}{e}=\frac{20000}{7} \mathrm{cal} \cdot \mathrm{min}^{-1}\)

= \(\frac{20000 \times 4.2}{7 \times 60} \mathrm{~J} \cdot \mathrm{s}^{-1}=200 \mathrm{~J} \cdot \mathrm{s}^{-1}\)

= 200 W.

Example 5. An ideal gas is kept in a closed, rigid, and heat-insulating vessel. A coil of resistance 100 ohm, carrying a current of 1 ampere, is supplying heat to the gas. What will be the change of internal energy of the gas?
Solution:

Given

An ideal gas is kept in a closed, rigid, and heat-insulating vessel. A coil of resistance 100 ohm, carrying a current of 1 ampere, is supplying heat to the gas.

Since the vessel is insulated, the exchange of heat Q = 0

Work done by electrical energy in 5 minutes i.e., 300 seconds, W = I²Rt = I² x 100 = 300 = 30000J

This work is supplied to the gas from outside. So it is negative, i.e., W = -30000 J.

From the first law of thermodynamics,

Q=(U_f – U_i)+W or, 0 = ΔU +(-30000)

[ΔU = U_f– U_i = change of internal energy] or, ΔU = 30000 J.

Difference Between Otto Cycle And Diesel Cycle

Example 6. A Carnot engine takes 3000 kcal of heat from a reservoir at 627°C. The sink is at 27°C. What is the amount of work done by the engine?
Solution:

Given

A Carnot engine takes 3000 kcal of heat from a reservoir at 627°C. The sink is at 27°C.

Temperature of the reservoir, T₁ = (627 + 273)K = 900K

Temperature of the sink, T₂ = (27 + 273)K = 300K

∴ Efficiency, \(\eta=1-\frac{T_2}{T_1}=1-\frac{300}{900}=\frac{2}{3}\)

Again, \(\eta=\frac{W}{Q_1},\)

W = \(\eta Q_1=\frac{2}{3} \times 3000\)

= \(2000 \mathrm{kcal}=2000 \times 4.2 \times 10^3 \mathrm{~J}\)

= \(8.4 \times 10^6 \mathrm{~J}\)

Applications Of Thermodynamic Cycles In Real Life

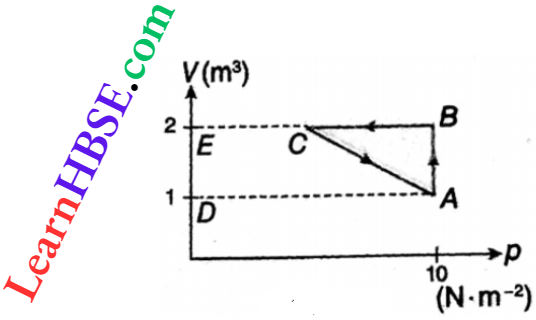
Example 7. An ideal gas is taken through the cycle A → B → C→A as shown in. If the net heat supplied to die gas in the cycle is 5 J, determine the work done by the gas in the process C → A.

Solution:

Heat taken by the gas, Q = 5 J

Since in the cycle A → B → C → A, the initial and the final states are both A, the change of internal energy, \(\Delta U=U_A-U_A=0\)

Now, \(W_{A B}\)= area of ABED = A D x E D = 10 x(2-1)=10 J

∴ \(W_{B C}=0\)

So, W = \(W_{A B}+W_{B C}+W_{C A}=10+W_{C A}\)

From the first law of thermodynamics, we have,

Q = \(\Delta U+W\)

or, 5 = \(0+\left(10+W_{C A}\right) \text { or, } W_{C A}=5-10=-5 \mathrm{~J} .\)

Explanation Of Thermodynamic Cycles For Beginners

Example 8. If a system is taken from i to f by the process i → a → f, Q is 50 cal and W is 20 cal. If in the process i → b → f, Q is 36 cal, what is the value of W?

Solution:

In both the processes, initial state i and final state f are the same.

So change of internal energy U_f– U_i is also equal.

In process \(i \rightarrow a \rightarrow f, U_f-U_i=Q-W=50-20=30 \mathrm{cal}\)

∴ In process \(i \rightarrow b \rightarrow f. U_f-U_i=Q-W\)

or, \(W=Q-\left(U_f-U_i\right)=36-30=6 \mathrm{cal}\).

Importance Of Thermodynamic Cycles In Engineering

Example 9. A thermodynamic process is shown. The pressures and volumes corresponding to some points in the figure are p_A = 3 x 10⁴ Pa; p_B = 8 x 10⁴ Pa; V_A = 2 x 10^-3 m³; V_D = 5 x 10^-3 m³. In process AB, 600 J of heat is added to the system, and in process BC, 200 J of heat is added. What would be the change in internal energy of the system in the process AC?

Solution:

Given

A thermodynamic process is shown. The pressures and volumes corresponding to some points in the figure are p_A = 3 x 10⁴ Pa; p_B = 8 x 10⁴ Pa; V_A = 2 x 10^-3 m³; V_D = 5 x 10^-3 m³. In process AB, 600 J of heat is added to the system, and in process BC, 200 J of heat is added.

Since AB is an isochoric process, no work is done.

∴ From the first law of thermodynamics,

Q = ΔU+ W or, 600 = ΔU+ 0 or, ΔU = 600 J

Again, work done in the process BC = area under the line BC

= P_B (V_D – V_B) = P_B(V_D – V_A)

= 8 x 10³ x (5 x 10^-3 – 2 x 10^-3) = 240 J .

∴ Q = ΔU+ W or, ΔU= Q-W= 200-240 = -40J

So, the change of internal energy in the process ABC = 600 – 40 = 560 J

Since internal energy is independent of the path, the change of internal energy in the process AC = 560 J.

Carnot Cycle Vs Rankine Cycle Comparison

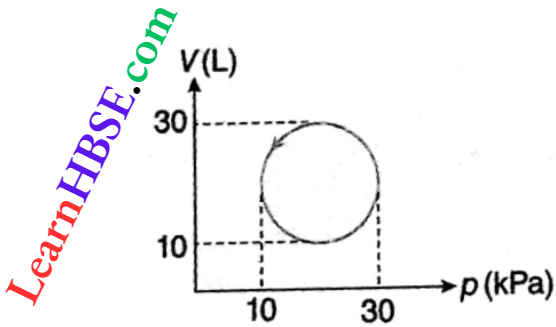
Example 10. What is the amount of heat energy absorbed by a system going through a cyclic process shown.

Solution:

The system is shown on a p-V diagram. In the diagram, the cycle is circular.

Radius of the cycle = \(\frac{30-10}{2}=10 \text { unit }\)

∴ Work done, W = area of the cycle

= π x 10² (litre x kPa)

= 100π x 10^-3 m³ x 10³ Pa

= 100π J = 100×3.141 = 314 J

In a cyclic process, change of internal energy = 0

So according to the first law of thermodynamics, Q = ΔU+ W = 0 + 314 = 314 J

Numerical Problems On Thermodynamic Cycles Class 11

Example 11. A thermodynamic system is taken through the cycle PQRSP. What is the net work done by the system?

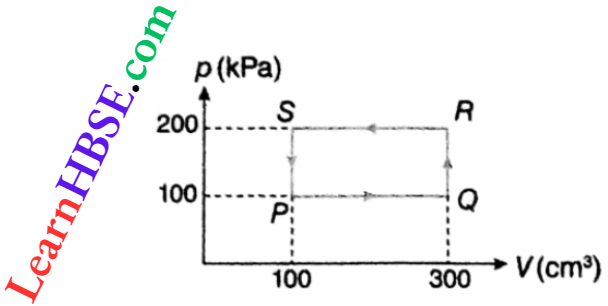
Solution:

Area of the cycle

= PQ · PS = (300 – 100)cm³ x (200 – 100) kPa

= 200 x 100 x 10^-6 m³ x 10³ Pa

= 20000 x 10^-3 J = 20J

Since the cycle is anticlockwise, work done is negative.

∴ W = -20J.

Example 12. A sample of an ideal monatomic gas is taken around the cycle ABC A. Calculate the work done during the cycle.

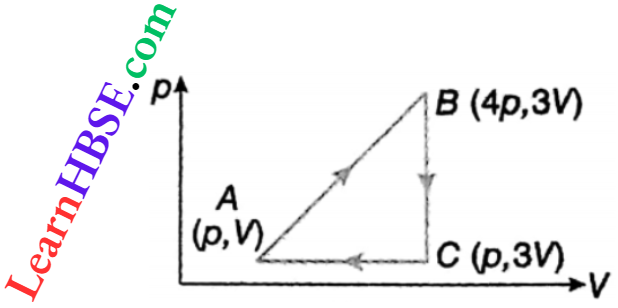
Solution:

Area of the cycle = \(\frac{1}{2}\) AC BC = \(\frac{1}{2}\)(3 V – V)(4 p-p) = 3pV

Since the cycle is clockwise, work done is positive.

∴ W=3pV.