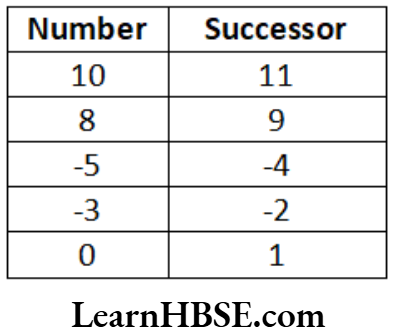
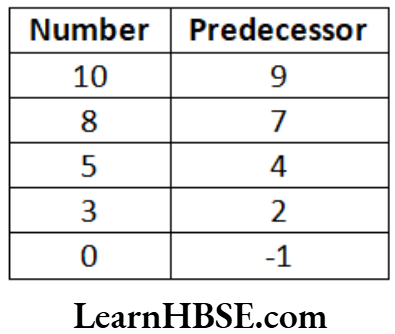
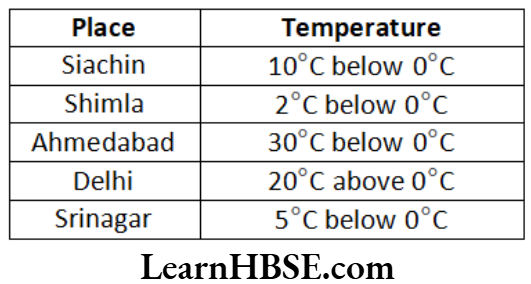
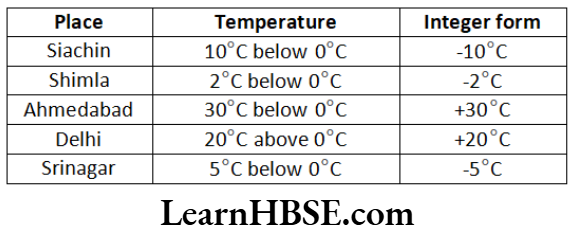
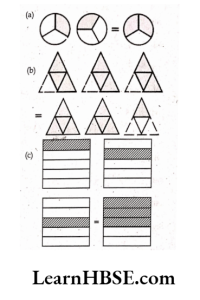
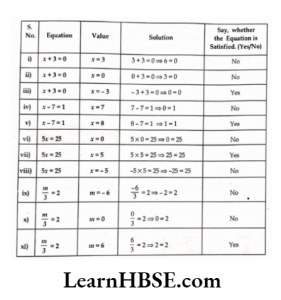
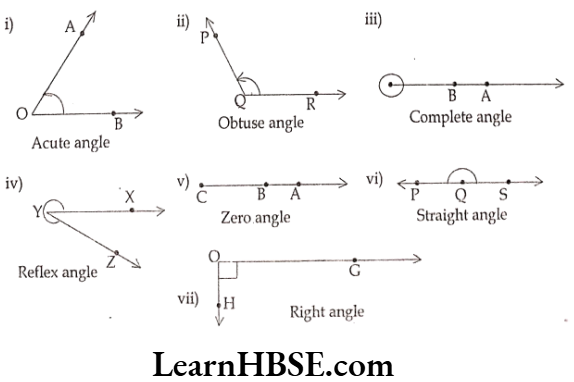
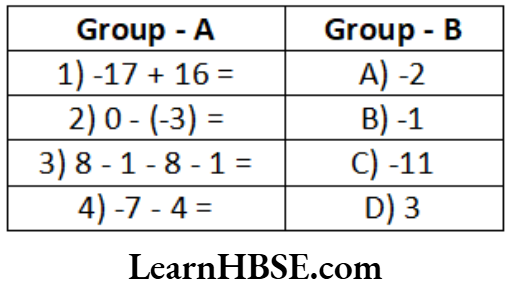Haryana Board Class 6 Maths Solutions For Chapter 10 Mensuration

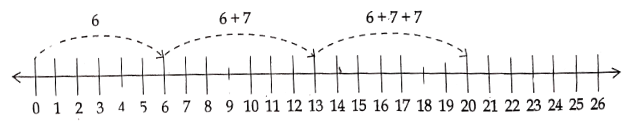
• Perimeter is the distance covered along the boundary forming a closed figure when you go round the figure once.
• The length of the boundary of a closed figure is called its ‘Perimeter’ (Or) Sum of all the lengths of a polygon is called its ‘Perimeter’.
• The perimeter of a rectangle = 2 [length + breadth]
• Perimeter of a square = 4 x [length of its side]
• Perimeter of a equilateral triangle = 3 x length of the side.
• Circumference [Perimeter] of a circle = πd (Or) 2πr
• The place occupied by an object is called area of the object. Area is measured in square units.
• Area of a rectangle = length x breadth
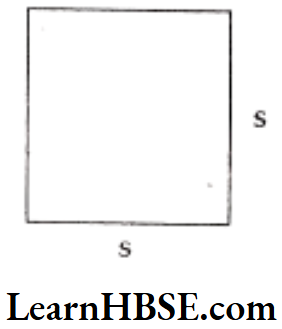
• Area of a square = side x side

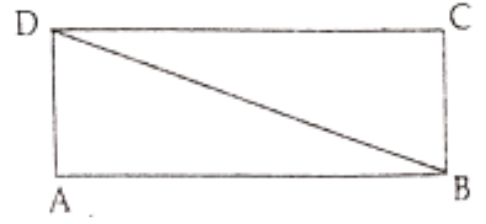
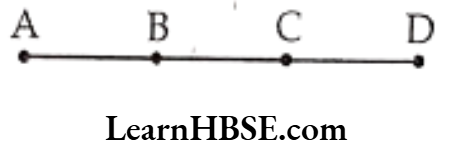
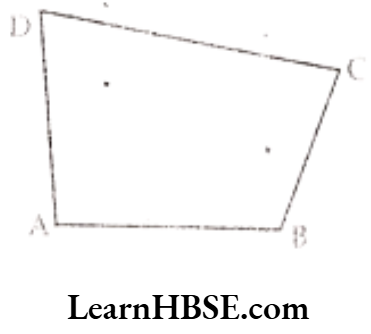
Question 1. Meera went to a park 150 m long and 80m wide. She took one complete round on its boundary. What is the distance covered by her?

Solution.

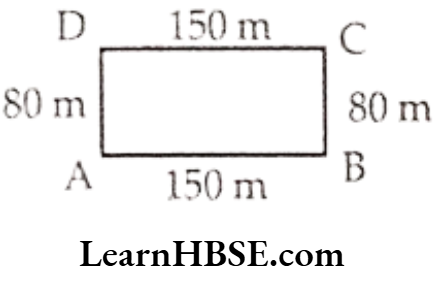
Distance covered by Meera

= AB + BC + DC + DA

= (150 + 80 + 150 + 80) m

= 460 m

Haryana Board Class 6 Maths Mensuration solutions

Question 2. Find the perimeter of the following figures:

Solution. a)

Perimeter

= AB + BC + CD + DA

= 40 m + 10 m + 40 m + 10m

= 100 m

b)

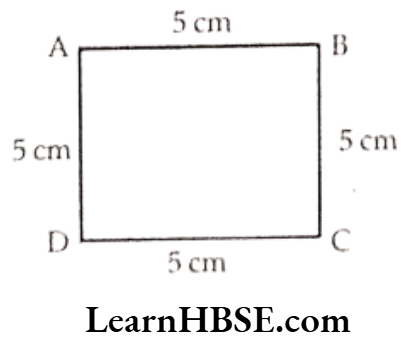
Perimeter

= AB + BC + CD + AD

= 5m + 5m + 5m + 5m

= 20 m

c)

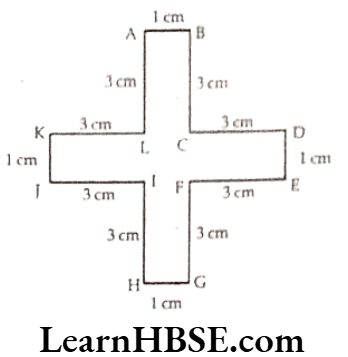
Perimeter

= AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + LA

= 1 cm + 3 cm + 3 cm + 1 cm + 3 cm + 3cm + 1 cm + 3 cm + 3 cm + 1 cm + 3 cm + 3 cm

= 28 cm

Perimeter and area formulas for Class 6 HBSE Maths

d)

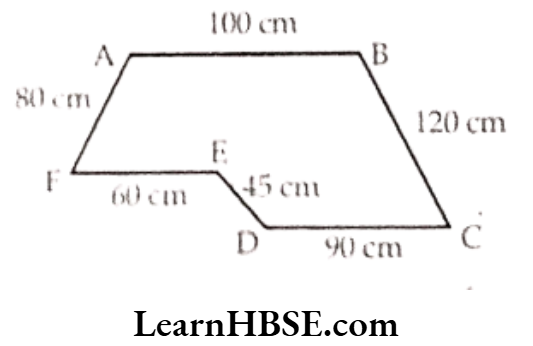
Perimeter

= AB + BC + CD + DE + EF + FA

= 100 m + 120 m + 90m + 45m + 60 m + 80 m

= 495 m

Question 3. Find the perimeter of the following rectangles:

Solution. 1) Perimeter = 2(1 + b) = 2 (0.5 m + 0.25 m)

= 2(0.75) m = 1.5 m

Perimeter by adding all the sides

= 0.5 + 0.25 + 0.5 + 0.25

= 1.5 m

2) Perimeter = 2(1 + b)= 2(18 cm + 15 cm) = 66 cm.

Perimeter by adding all the sides

= 18 + 15 + 18 + 15 = 66 cm.

3) Perimeter = 2(1 + b)

= 2 (10.5 cm + 8.5 cm)

= 2 (19 cm) = 38 cm.

Perimeter by adding all the sides

= 10.5 + 8.5 + 10.5 + 8.5

= 38 cm.

Volume of cube and cuboid Class 6 HBSE Maths

Question 4. Find various objects from your surroundings which have regular shapes and find their perimeters.

1) Square:

Solution. 1) A square has four equal sides.

2) Let’s assume the length of one side is 5 cm.

3) The perimeter of a square is calculated by multiplying the length of one side by 4.

4) Therefore, the perimeter of the square would be 5 cm x 4 = 20 cm.

2) Rectangle:

Solution. 1) A rectangle has two pairs of equal sides (opposite sides)

2) Let’s assume the length of one side is 6 cm and the length of the adjacent side is 8 cm.

3) The perimeter of a rectangle is calculated by adding the lengths of all four sides.

4) Therefore, the perimeter of the rectangle would be (6 cm + 8 cm) x 2 = 28 cm..

3) Circle:

Solution. 1) A circle is a curved shape with a constant radius.

2) Let’s assume the radius of a circle is 3 cm.

3) The perimeter of a circle is called its circumference and is calculated using the formula: 2 × π × radius.

4) Therefore, the perimeter (circumference) of the circle would be

2 x 3.14 x 3 cm = 18.84 cm.

Please note that these are just examples, and the actual objects around you may have different dimensions and perimeters.

Haryana Board Class 6 Maths Solutions For Chapter 10 Mensuration Exercise 10.1

Question 1. Find the perimeter of each of the following figures:

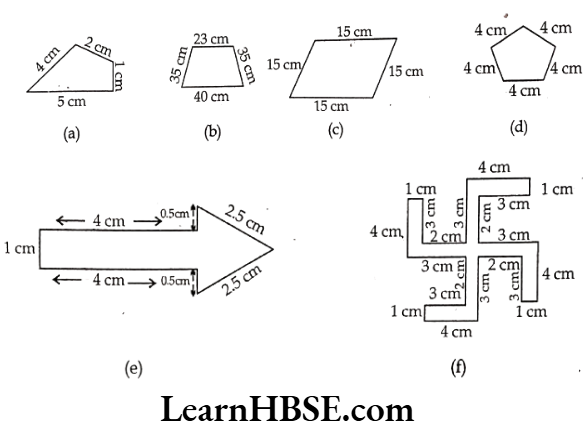
Solution. a) Perimeter

5 cm + 1 cm + 2 cm + 4 cm

= 12 cm

b) Perimeter

= 40 cm + 35 cm + 23 cm + 35 cm

= 133 cm

c) Perimeter =

= 15 cm + 15 cm + 15 cm + 15 cm

= 60 cm

d) Perimeter = 4 cm + 4 cm + 4 cm + 4 cm + 4 cm = 20 cm

e) Perimeter = 1 cm + 4 cm + 0.5 cm + 2.5 cm + 2.5 cm + 0.5cm + 4cm = 15cm

f) Perimeter = 1 cm + 3 cm + 2 cm + 3 cm + 4 cm + 1 cm + 3 cm + 2 cm + 3 cm + 4 cm + 1 cm, + 3 cm + 2 cm + 3 cm + 4 cm + 1 cm + 3 cm + 2 cm + 3 cm + 4 cm = 52 cm

Circumference and area of a circle Class 6 Haryana Board

Question 2. The lid of a rectangular box of sides 40 cm by 10 cm is sealed all round with tape. What is the length of the tape required?

Solution. Length of rectangular box = 40 cm

Breadth of rectangular box = 10 cm

Length of the tape required

= 2 (length + breadth)

= 2(40 cm + 10 cm)

= 2 × 50 cm

= 100 cm

= 1 m

Question 3. A table top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the table-top?

Solution. Length = 2 m 25 cm = 2.25 m

Breadth = 1 m 50 cm = 1.5 m

Perimeter of top of the table

= 2(length + breadth)

= 2(2.25 + 1.5) m.

= 2(3.75 m)

= 7.5 m.

Question 4. What is the length of the wooden strip required to frame a photograph of length and breadth 32 cm and 21 cm respectively?

Solution. Length = 32 cm

Breadth = 21 cm

Length of wooden strip required

= 2(length + breadth)

= 2(32 + 21) cm

= 2 x 53 cm

= 106 cm.

Question 5. A rectangular piece of land measures 0.7 km by 0.5 km. Each side is to be fenced with 4 rows of wires. What is the length of the wire needed?

Solution. Length = 0.7 km

Breadth = 0.5 km

Perimeter of a rectangle

= 2 (length + breadth)

= 2 (0.7 km + 0.5 km)

= 2.4 km.

Length of wire needed

= 4 × perimeter

= 4 × 2.4 km

= 9.6 km.

Mensuration Class 6 HBSE important questions

Question 6. Find the perimeter of each of the following shapes.

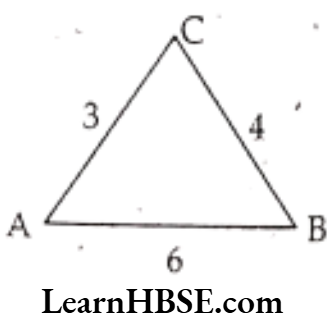
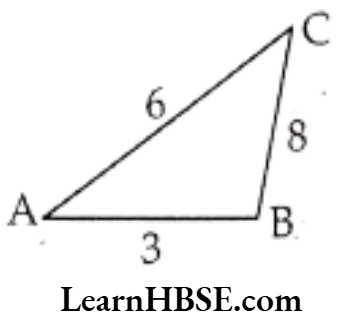
a) A triangle of sides 3 cm, 4 cm, and 5 cm.

Solution. Perimeter of the triangle

= 3 cm + 4 cm + 5 cm

= 12 cm

b) An equilateral triangle of side 9 cm.

Solution. Perimeter = 9 cm + 9 cm + 9 cm

= 27 cm

c) An isosceles triangle with equal sides 8 cm each and third side 6 cm.

Solution. Perimeter of an isosceles triangle

= 8 cm + 8 cm + 6 cm

= 22 cm

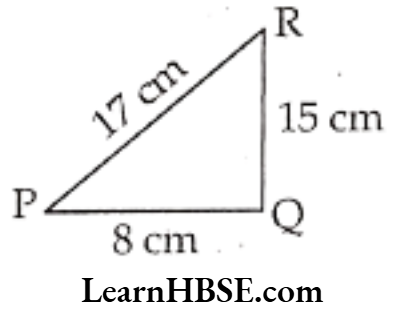
Question 7. Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.

Solution. Perimeter of the triangle

= Sum of the lengths of sides

= 10 cm + 14 cm + 15 cm

= 39 cm.

Question 8. Find the perimeter of a regular hexagon with each side measuring 8 m.

Solution. Perimeter of regular hexagon

= 6 x length of side

= 6 × 8 m

= 48 m.

Question 9. Find the side of the square whose perimeter is 20 m.

Solution. Perimeter of square = 20 m

4 x length of the side = 20 m

Length of the side = \(\frac{20 \mathrm{~m}}{4}=5 \mathrm{~m}\)

Question 10. The perimeter of a regular pentagon is 100 cm. How long is its each side?

Solution. Perimeter of regular pentagon = 100 cm

5 x length of the side = 100 cm

Length of the side = \(\frac{100 \mathrm{~cm}}{5}=20 \mathrm{~cm} .\)

Question 11. A piece of string is 30 cm long. What will be the length of each side if the string is used to form:

a) a square?

b) an equilateral triangle ?

c) a regular hexagon?

Solution. a) Perimeter of a square = 30 cm

4 × length of side = 30 cm

length of side = \(\frac{30 \mathrm{~cm}}{4}=7.5 \mathrm{~cm}\)

b) Perimeter of equilateral triangle = 30 cm.

3 x length of side = 30 cm

Length of side = \(\frac{30 \mathrm{~cm}^{\prime}}{3}=10 \mathrm{~cm} .\)

c) Perimeter of regular hexagon = 30 cm

6 x length of side = 30 cm

Length of side = \(\frac{30 \mathrm{~cm}}{6}=5 \mathrm{~cm} .\)

Question 12. Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is the third side?

Solution. Perimeter of a triangle = Sum of the lengths of 3 sides

36 cm = 12 cm + 14 cm + length of third side

36cm = 26 cm + length of third side

∴ length of third side

= 36 cm – 26 cm = 10 cm

Question 13. Find the cost of fencing a square park of side 250 m at the rate of ₹ 20 per metre.

Solution. Perimeter of square park

= 4 x length of one side.

= 4 x 250 m

= 1000 m

∴ Cost of fencing at the rate of ₹ 20 per metre.

= ₹ 1000 x ₹ 20

= ₹ 20,000

Question 14. Find the cost of fencing a rectangular park of length 175 m and breadth 125 m at the rate of ₹ 12 per metre.

Solution. Perimeter of a rectangular park

= 2(length + breadth)

= 2(175 + 125)m

= 2(300)m

= 600 m

∴ Cost of fencing the rectangular park at the rate of ₹ 12 per metre.

= ₹ 12 × ₹ 600

= ₹ 7200

Question 15. Sweety runs around a square park of side 75 m. Bulbul runs around a rectangular park with length 60 m and breadth 45m. Who covers less distance?

Solution. Perimeter of a square park

= 4 x length of one side

= 4 x 75 m.

= 300 m.

Perimeter of a rectangular park

= 2(1 + b)

= 2 (60 m + 45 m)

= 2 (105 m)

= 210 m

here 300 m > 210 m

∴ Bulbul covers less distance.

Question 16. What is the perimeter of each of the following figure? What do you infer from the answers?

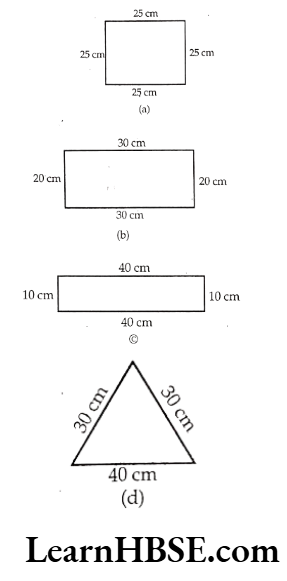
Solution. a) Perimeter = 25 cm + 25 cm + 25 cm +25 cm 100 cm.

b) Perimeter = 30 cm + 20 cm + 30 cm + 20 cm = 100 cm

c) Perimeter = 40 cm + 10 cm + 40 cm +10 cm = 100 cm

d) Perimeter = 40 cm + 30 cm + 30 cm = 100 cm

Inference: The perimeter of all the fig- ures is 100 cm.

Question 17. Avneet buys 9 square paving slabs, each with a side of \(\frac{1}{2}\) m. He lays them in the form of a square.

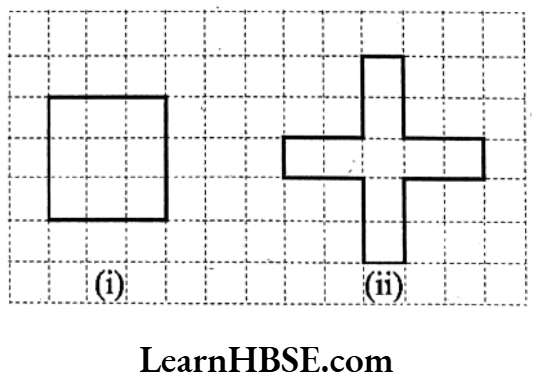
a) What is the perimeter of his arrangement in the above figure (1)?

b) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement in the above figure (2)?

c) Which has greater perimeter?

d) Avneet wonders if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges i.e. they can- not be broken.)

Solution. a) Perimeter of the figure(1) = 4 x side

Length of the side of the square

= 3 x square

Slabs x length of each side

= 3 x 0.5 m = 1.5 m(each side = \(\frac{1}{2}\)m)

Perimeter of Avneet’s arrangement

= 4 x 1.5m = 6m.

b) Peimeter of the figure (2)

= 5 x length of each side

= 5 x 0.5 = 2.5 m (each side = \(\frac{1}{2}\)m)

Perimeter of the cross = 4 x figure

= 4 x 2.5 = 10 m

c) Shari’s arrangement has greater perimeter.

d) No, but we can achieve the same perimeter as shari’s arrangement by arranging all the squares in a row.

Haryana Board Class 6 Maths Solutions For Chapter 10 Mensuration Exercise 10.2

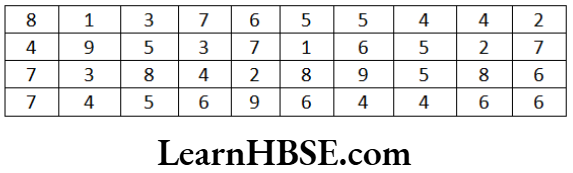
Question 1. Find the areas of the following figures by counting squares.

Solution. a)

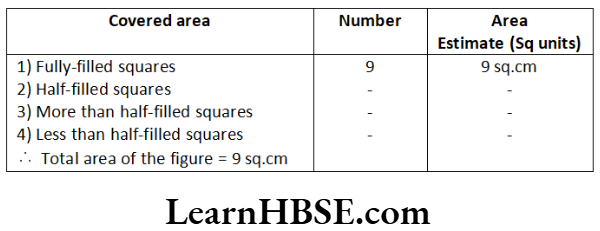
b)

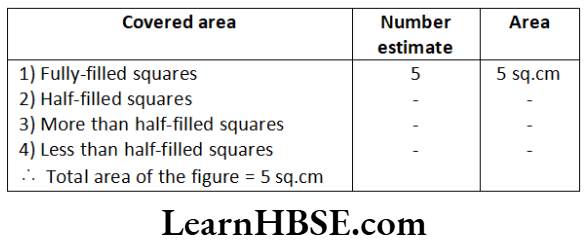
∴ Total area of the figure = 5 sq.cm

c) Fully-filled squares = 2

Half-filled squares = 4

Area covered by fully squares = 2 × 1 = 2 sq. cm

Area covered by half squared = 4 x \(\frac{1}{2}\) = 2 sq. cm

Total area = 4 sq.cm.

d) Fully-filled squares = 8

∴ Total area = Area covered by full squares

=8 × 1 sq.cm

= 8 sq. cm

e) Fully filled squares = 10

∴ Total area = Area covered by full squares

= 10 × 1 sq cm.

= 10 sq.cm.

f) Fully-filled squares = 2

Half-filled squares = 4

Area covered by fully squares = 2 x 1 sq.cm

= 2 sq.cm

Area covered by half squares = 4 x \(\frac{1}{2}\) sq.cm

= 2 sq. cm.

∴ Total area = 2 sq.cm + 2 sq.cm

= 4 sq.cm

g) Fully-filled squares = 4

Half-filled squares = 4

Area covered by full squares

= 4 x 1 sq. cm = 4 sq. cm

Area covered by half squares

= 4 x \(\frac{1}{2}\) sq. cm = 2 sq. cm

∴ Total area 4 sq. cm + 2 sq. cm

= 6 sq. cm.

h) Fully-filled squares = 5

∴ Total area = Area covered by full squares

= 8 x 1 sq. cm = 5 sq. cm

i) Fully-filled squares = 9

∴ Total area = Area covered by full squares

= 9 × 1 sq. cm

= 9 sq. cm

j) Fully-filled squares = 2

Half filled squares = 4

Area covered by full squares

= 2 x 1 sq. cm

= 2 sq. cm

Area covered by half squares

= 4 x \(\frac{1}{2}\) sq.cm = 2 sq.cm

∴ Total area 2 sq. cm + 2 sq. cm

= 4 sq. cm

k) Fully filled squares = 4

Half filled squares = 2

Area covered by full squares

= 4 × 1 sq. cm

= 4 sq. cm

Area covered by half squares

= 2 x \(\frac{1}{2}\) sq.cm

= 1 sq. cm

∴ Total area = 4 sq. cm + 1 sq. cm

= 5 sq. cm

1) Fully-filled squares = 4 = 4 sq.cm

Half-filled squares

= 2 = 2 x \(\frac{1}{2}\) = 1 sq.cm

More than half filled squares

= 3 = 3 x 1 sq cm = 3 sq.cm

∴ Total area

= 4 sq. cm + 3 sq. cm

= 7 sq.cm

m) Fully filled squares = 7 x 1 sq.cm

= 7 sq.cm

Half-filled squares = More than half filled squares

= 7 x 1 sq.cm = 7 sq.cm

Less than half filled squares = 4

Total area = 7 sq. cm + 7sq.cm

= 14 cm.

n) Fully filled squares = 9 x 1 = 9 sq.cm

Half-filled squares

More than half filled squares

= 9 x 1 = 9 sq.cm

Total area = 9 sq. cm + 9 sq.cm

= 18 sq.cm

Question 2. Find the area of the floor of your classroom.

Solution. Let’s assume the length of the classroom is 10 meters and the width is 8 meters.

Area = 10 meters x 8 meters = 80 sq.m.

So, the area of the floor of the classroom would be 80 sq m.

Question 3. Find the area of any one door in your house.

Solution. The most common standard door size is 80 inches (6.67) feet) in height and 36 inches (3 feet) in width area of door

= Height x Width

Area of door = 80 inches x 36 inches = 2880 sq. inches.

To convert square inches to square feet, divide the area by 144 (since there are 144 square inches in a square foot):

Area of door (in square feet) = 2880 square inches/144 = 20 square feet.

There fore, the approximate area of standard -size door in a house is around 20 square feet.

Haryana Board Class 6 Maths Solutions For Chapter 10 Mensuration Exercise 10.3

Question 1. Find the areas of the rectangles whose sides are:

a) 3 cm and 4 cm

b) 12 m and 21 m

c) 2 km and 3 km

d) 2 m and 70 cm

Solution. a) 1 = 4 cm, b = 3 cm

Area of rectangle = 1 x b

= 4 x 3

= 12 sq. cm.

b) 1 = 21 m, b = 12 m

Area of rectangle = 1 x b

= 21 × 12

= 252 sq.m.

c) 1 = 3 km, b = 2 km

Area of rectangle = 1x b

= 3 × 2

= 16 sq.km.

d) 1 = 2 m, b = 70 cm = 0.7 m

Area of rectangle = 1 x b

= 2 × 0.7

= 1.4 sq.m.

Question 2. Find the areas of the squares whose sides are:

a) 10 cm

b) 14 cm

c) 5 m

Solution. a) a = 10 cm

Area of the square a² sq. cm

= 10² sq. cm

= 100 sq. cm

b) a = 14 cm

Area of the square = a² sq. cm

= 14² sq. cm

= 196 sq. cm

c) a = 5 m

Area of the square = a²

= 5² sq.cm

= 25 sq.cm

Question 3. The length and breadth of three rectangles are as given below:

a)9 m and 6 m

b) 17 m and 3 m

c) 4 m and 14 m

Which one has the largest area and which one has the smallest ?

Solution. a) 1 = 9 m, b = 6m

Area of rectangle = l x b

= 9 x 6

= 54 sq.m.

b) 1 = 17 m, b = 3 m

Area of rectangle = 1 x b

= 17 × 3

= 51 sq. m.

c) 1 = 14 m, b = 4m

Area of rectangle

= 1 x b

= 14 × 4

= 56 sq.m

The rectangle(c) has the largest area and the rectangle (b) has the smallest area.

Word problems on Mensuration for Class 6 HBSE

Question 4. The area of a rectangular garden 50 m long is 300 sq.m. Find the width of the garden.

Solution. Area of a rectangular garden = 300 sq.m.

length = 50 m.

1 x b = 300

50 x b = 300

b = \(\frac{300}{50}\) m

b = 6m

∴ Width of the garden = 6m

Question 5. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of 8 per hundred sq. m.?

Solution. Length of a rectangular piece of land = 500 m

Breadth of a rectangular piece of land = 200 m

Area = length x breadth

= 500 m × 200 m

= 1,00,000 sq.m.

Cost of tiling per 100sq. m = ₹ 8

Cost of tiling 1,00,000 sq. m

= \(₹ \frac{8}{100} \times 100000\)

= ₹ 8000

Question 6. A table-top measures 2 m by 1 m 50 cm. What is its area in square metres?

Solution. Length of the table = 2 m

Breadth of the table = 1 m 50 cm = 1.5 m

Area of the table = length x breadth

= 2 × 15 sq.m

= 3 sq.m.

Question 7. A room is 4m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?

Solution. Length of the room = 4 m = 4 m

Breadth of the room = 3 m 50 cm

= 3.50 m

∴ Area of the room

= length x breadth

= 4m x 3.50 m

= 14 sq.m.

∴ 14 sq. m of carpet is needed to cover the floor.

Question 8. A floor is 5m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.

Solution. Length of the floor = 5 m

Breadth of the floor = 4 m

Area of the floor = length x breadth

= 5 x 4 sq. m

= 20 sq.m

Area of the square carpet = a2

= (3)2 sq. m

= 9 sq. m.

Area of the floor that is not carpeted

= 20 sq.m. – 9 sq.m

= 11 sq.m.

Question 9. Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of land?

Solution. Area of square flower bed = a² sq. m

=(1)²sq. m

= 1 sq. m

∴ Area of 5 square flower beds

= 1 x 5 sq. m

= 5 sq. m

Length of the piece of land = 5 m

Breadth of the piece of land

= length x breadth

= 4 x 5 sq. cm

= 20 sq. m

Area of remaining part of land

= 20 sq. m – 5 sq. m

= 15 sq. m

Question 10. By splitting the following figures into rectangles find their areas.

(The measures are given in centimetres)

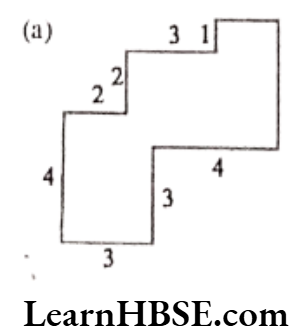
Solution. a) Area of the figure

= (3 x 3) + (1 x 2) + (3 x 3) + (4 × 2) sq. cm

= 9 + 2 + 9 + 8 sq.cm

= 28 sq. cm

b) Area of the figure

= (3 x 1 + 3 x 1 + 3 x 1) sq. m

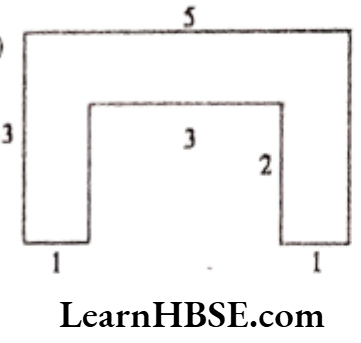
= 3 + 3 + 3 sq. cm

= 9 sq. cm

Question 11. Split the following shapes into rectangles and find their areas. (The measures are given in centimetres)

Solution. a)

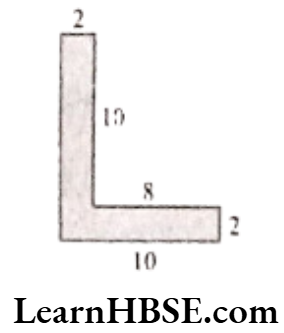
Area of the shape

= (8 x 2 + 12 x 2) sq. cm

= 16 + 24 sq. cm

= 40 sq. cm

b)

Area of the shape

= (7×7) + (7×7) + (7×7) + (7×7) + (7×7) sq.m

=(49 + 49 + 49 + 49 + 49) sq. m

= 245 sq. cm

c)

Area of the shape

= (5 x 1)+(4 x 1) sq. cm

= (5 + 4) sq. cm

= 9 sq. cm

Question 12. How many tiles whose length and breadth are 12 cm and 15 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively.

a) 100 cm and 144 cm

Solution. 1 = 144 cm, b = 100 cm

Area of rectangle = 1 x b

= 144 × 100

= 14400 sq.cm

Length of the tile = 5 cm

Breadth of the tile = 12 cm

Area of rectangle = 1 x b

= 5 x 12 sq.cm

= 60 sq.cm

∴ Number of tiles needed to fit the

region = \(\frac{\text { Area of theregion }}{\text { Area of tile }}\)

= \(\frac{14400}{60}\) = 240.

b) 70 cm and 36 cm

Solution. 1 = 70 cm, b = 36 cm

Area of the region = 70 × 36 sq.cm = 2520 sq.cm

Area of the tile = 60 sq.cm

Number of tiles needed = \(\frac{2520}{60}\)

= 42 sq.cm

A challenge!

On a centimetre squared paper, make as many rectangles as you can, such that the area of the rectangle is 16 sq cm (consider only natural number lengths).

a) Which rectangle has the greatest perimeter?

b) Which rectangle has the least perimeter? If you take a rectangle of area 24 sq cm, what will be your answers? Given any area, is it possible to predict the shape of the rectangle with thegreatest perimeter? With the least perimeter? Give example and reason.

Solution. Three rectangles can be made as follows:

1) Sides 16 cm and 1 cm

Perimeter = 2(1 + b)

= 2(16 + 1) = 34 cm

2) Sides 8 cm and 2 cm

Perimeter = 2(l + b)

= 2(8 + 2) = 20 cm

3) Sides 4 cm and 4 cm

Perimeter = 2(l + b)

= 2(4 + 4) = 16 cm

a) The rectangle (1) has the greatest perimeter.

b) The rectangle (3) has the least perimeter. If the area is 24 sq. cm. Four rectangles can be made as follows.

1) Sides 24 cm and 1 cm

Perimeter = 2(1 + b)

= 2(24 + 1) = 50 cm

2) Sides 4 cm and 6 cm

Perimeter = 2(1 + b)

= 2(4 + 6) = 20 cm

3) Sides 8 cm and 3 cm

Perimeter = 2 (1 + b)

= 2(8 + 3) = 22 cm

4) Sides 12 cm and 2 cm

Perimeter = 2(l + b)

= 2(12 + 2) = 28 cm

Yes! it is possible to predict the shape of the rectangle with the (1) greatest perimeter. 2) least perimeter.

Difference between perimeter and area Class 6

Haryana Board Class 6 Maths Solutions For Chapter 10 Mensuration Very Short Answer Questions

Question 1. Find the perimeters of the given figures.

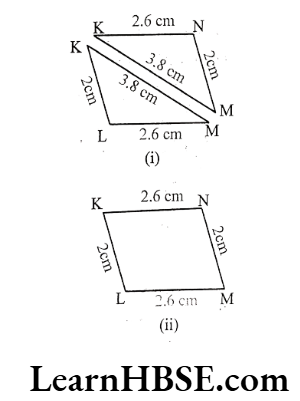
In the above figures (1) and (2), find the perimeter of ΔKLM, ΔKMN and ▢KLMN.

Solution. 1) Perimeter of ΔKLM

= KL + LM + KM

= 2 + 2.6 + 3.8 = 8.4 cm

Perimeter of ΔKMN

= KM + MN + KN

= 3.8 + 2 + 2.6 = 8.4 cm

2) Perimeter of ▢KLMN

= KL + LM + MN + KN

= 2 + 2.6 + 2 + 2.6 = 9.2 cm

Question 2. Find the perimeters of the following figures.

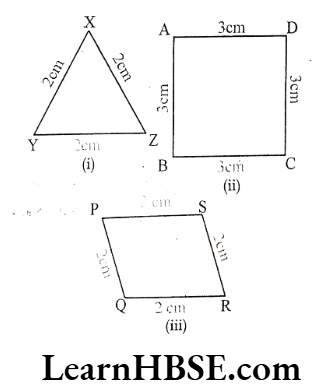
Solution. Perimeter of AXYZ

= XY + YZ + XZ

= 2 + 2 + 2 = 6 cm

2) Perimeter of a square ABCD

= AB + BC + CD + AD

= 3 + 3 + 3 + 3 = 12 cm

3) Perimeter of ▢PQRS

= PQ + QR + RS + PS

= 2 + 2 + 2 + 2 = 8 cm

Question 3. Find the area of a square with side 16 cm.

Solution.

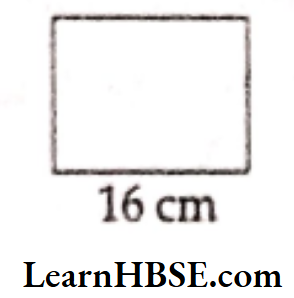
Length of the side of a square = 16 cm

Area of a square = side x side

= 16 x 16 = 256 cm²

Question 4. Length and breadth of a rectangle are 16 cm and 12 cm respectively. Find its

Solution.

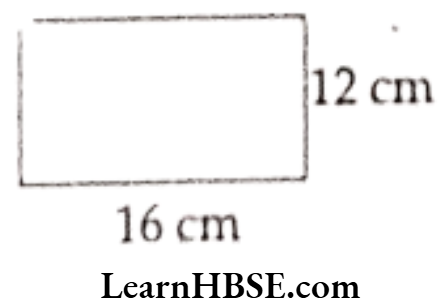
Length of a rectangle l = 16 cm

Its breadth = b = 12 cm

Area of a rectangle

= 1 x b

= 16 × 12

= 192 cm²

Question 5. Find the area of the rectangle of measurements 15cm and 8cm as length and breadth respectively.

Solution.

Length of a rectangle = 1 = 15 cm

Its breadth = b = 8 cm

Area of a rectangle = l x b

= 15 x 8

= 120 cm²

Question 6. Find the area of a square whose perimeter is 64m.

Solution. Perimeter of a square = 64 m

Perimeter of a square

= 4 x side(s)

= 4 x s = 64

s = \(\frac{64}{4}\) = 16

Side of a square(s) = 16 m

∴ Area of a square = s x s

= 16 x 16 = 256 m²

Question 7. Ritu went to a park 130 m long and 90 m wide. She took one complete round of it. What distance did she cover?

Solution.

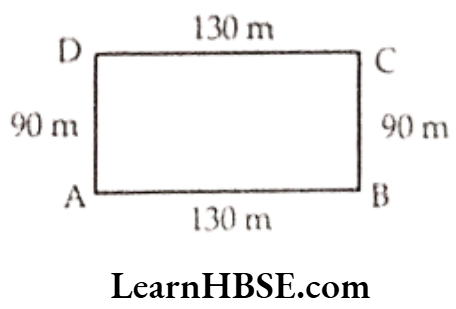
Total distance covered by Ritu = Perimeter of the park ABCD

= AB + BC + CD + DA

= 130 + 90 + 130 + 90

= 440 m.

Question 8. Find the perimeter of given shape.

Solution.

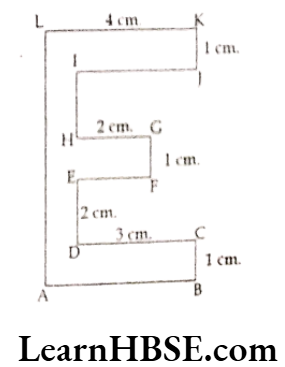
IJ = DC = 3 cm; EF = HG = 2 cm

AB = LK = 4 cm; FG = KJ = CB = 1 cm

AL = BC + DE + FG + HI + JK

= 1 + 2 + 1 + 2 + 1 = 7 cm.

Perimeter

= AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + LA

= 4 + 1 + 3 + 2 + 2 + 1 + 2 + 2 + 3 + 1 + 4 + 7 = 32 cm.

Question 9. Length and breadth of a rectangle are 15 cm. and 10 cm. Find the perimeter.

Solution. Length of the rectangle = 15 cm.

Breadth = 10 cm.

Perimeter of the rectangle

= 2 (length + breadth)

= 2 (15 + 10)

= 2 x 25 = 50 cm.

Question 10. Find the perimeter of a rectangular field which is 36 m. long and 24 m. wide.

Solution. Length of the rectangle field (1) = 36 m.

Breadth of the field (b) = 24 m.

∴ Perimeter of the field = 2(1 + b)

= 2(36 + 24)

= 2 x 60 = 120 m.

Haryana Board Class 6 Maths Solutions For Chapter 10 Mensuration Short Answer Questions

Question 11. Find the perimeter of

1) An equilateral triangle whose side is 3.5 cm.

Solution.

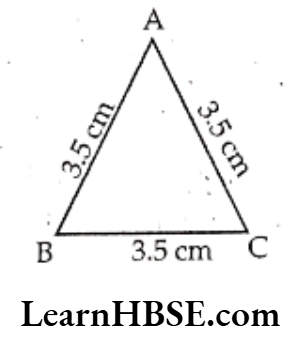
The length of the side of an equilateral triangle = 3.5 cm

Perimeter of an equilateral triangle

= 3 x length of the side

= 3 x 3.5 – 10.5 cm

2) A square whose side is 4.8 cm.

Solution.

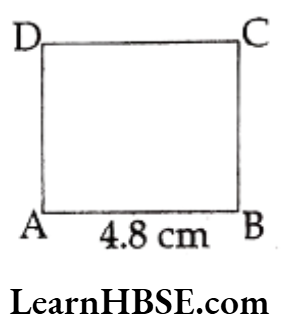
The length of the side of a square = s = 4.8 cm

Perimeter of square

= 4 x length of the side

= 4 x 4.8 = 19.2 cm

Question 12. Length and breadth of top of one table is 160cm and 90cm respectively. Find how much length of beading is required for each table.

Solution.

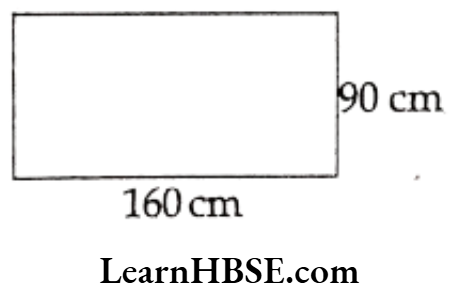
A table is in the shape of a rectangle.

Length of a table = l = 160 cm

Its breadth = b = 90 cm

∴ The length of beading is required for each table

= Perimeter of the rectangular table.

= 2[1 + b]

= 2[160 + 90] = 2 × 250 = 500 cm

Question 13. Find the perimeter and area of a square of side 4 cm. Are these same? Give some examples to support your answer.

Solution. Length of the side of a square = 4 cm Perimeter of a square

= 4 x side = 4 x 4 = 16 cm

Area of a square = s² = 4² = 16 cm²

In this condition perimeter and area of a square are equal.

For example length of the side be 6 cm.

Perimeter of a square

= 4 x s = 4 x 6 = 24 cm

Area of a square = s x s

= 6 × 6 = 36 cm

∴ Perimeter and area of a square need not be equal for all conditions.

Question 14. Find the area of the square whose perimeter is 48cm.

Solution. Perimeter of a square = 48 cm

Perimeter of a square = 4 × side

∴ 4 × side = 48

Side = \(\frac{48}{4}\) = 12

∴ Side of the square (s) = 12 cm

∴ Area of the square = s x s

= 12 x 12 = 144cm²

Haryana Board Class 6 Maths Solutions For Chapter 10 Mensuration Long Answer Questions

Question 15. Measurements of two rectangular fields are 50m x 30m and 60m x 40m. Find their perimeters. Check whether the perimeters are 2 x length + 2 x breadth.

Solution. Measurements of rectangle ABCD:

Length (l) Breadth (b)

Breadth (b)= 30 m

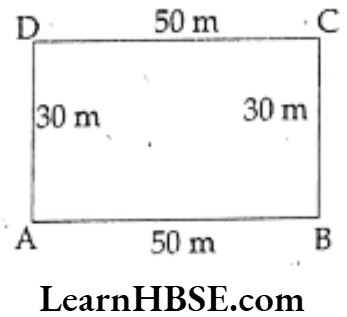
Perimeter of ▢ABCD

= AB + BC + CD + AD

= 50 + 30 + 50 + 30

= 160 m

Perimeter of ▢ABCD

=2 x length + 2 x breadth

= 2 (50) + 2 (30)

= 100 + 60

= 160 m

Yes, it is true.

Length of rectangle PQRS = l = 60 m

Breadth (b) = 40 m

Perimeter of ▢PQRS

= PQ + QR + RS + PS

= 60 + 40 + 60 + 40

= 200 m

Perimeter of ▢PQRS

= 2 x length + 2 x breadth

=2 x 60 + 2 x 40

= 120 + 80.

= 200 m

Yes, it is true.

Question 16. Manasa has 24 cm of metallic wire with her. She wanted to make some polygons with equal sides whose sides are integral without milling into pieces values. Find how many such polygons she can make with the metallic wire?

Solution. The length of the wire that Manasa has = 24 cm

She has to make some polygons with equal sides i.e., [squares] whose sides are integral without milling into pieces values.

∴ The smallest length of the side of a polygon [square],

she wants to make is (s) = 1 cm

Perimeter of one polygon [square]

= 4 x side

= 4 x 1 = 4 cm

∴ Number of polygons [square] that she can make with the length of 24 cm metallic wire

= \(\frac{\text { Length of the wire }}{\text { Perimeter of } 1 \text { square }}=\frac{24}{4}=6\)

Question 17. Find the perimeter of the following figures (1) and (2).

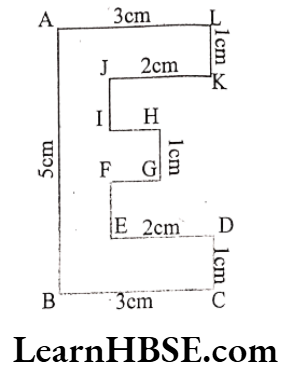
Solution. The perimeter of figure (1) ABCDEFGHIJKL

= AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + AL

= 5 + 3 + 1 + 2 + 1 + 1 + 1 + 1 + 1 + 2 + 1 + 3 = 22 cm

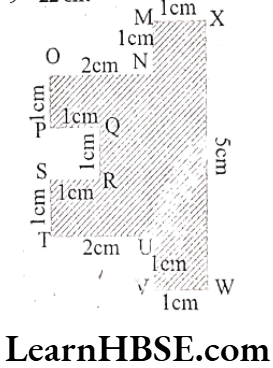
The perimeter of figure (2) MNOPQRSTUVWX

= MN + NO + OP + PQ + QR + RS + ST + TU + UV + VW + WX + MX

= 1 + 2 + 1 + 1 + 1 + 1 + 1 + 2 + 1 + 1 + 5 + 1 = 18 cm

Question 18. If the length of a rectangle is 14cm and its perimeter is 3 times of its length. Find its area.

Solution. Length of a rectangle = 1 = 14cm

Its perimeter = 3 x length of a rectangle

= 3 x 14 = 42 cm

∴ Perimeter of a rectangle = 2 [1 + b]

= 2[14 + b] cm.

∴ By the problem 2[14 + b] = 42

14 + b = \(\frac{42}{2}\)

14+ b = 21

b = 21 – 14 = 7

∴ Breadth of a rectangle = b = 7 cm

∴ Area of a rectangle = 1 x b

= 14 x 7 = 98 cm²

Question 19. 14cm and 12cm are the length and breadth of a rectangle. If the breadth is increased by 6cm and length is decreased by 6cm, find the difference in areas.

Solution. Length of a rectangle = l = 14cm

Its breadth = b = 12 cm

Area of a rectangle = l x b

= 14 x 12 = 168 cm²

If the breadth is increased by 6 cm and length is decreased by 6 cm then so formed.

Length = l = (l – 6) cm;

breadth = b = (b + 6) cm = 14 – 6 = 8 cm

∴ Area of so formed rectangle

= l x b

12 + 6 = 18 cm

Area of new rectangle = 1 x b

= 8 × 18

= 144 cm²

∴ Difference in areas

= 168 cm² – 144 cm²

= 24 cm²

Haryana Board Class 6 Maths Solutions For Chapter 10 Mensuration Objective Type Questions

Choose the correct answer:

Question 1. Perimeter of an equilateral triangle of side ‘s’ is

1. 4s
2. 2s
3. 3s
4. 6s

Answer. 3. 3s

Question 2. Perimeter of a regular hexagon of side 2 cm is

1. 12 cm
2. 10 cm
3. 8 cm
4. 12 sq.cm.

Answer. 1. 12 cm

Question 3. The space occupied by a closed figure is called its

1. area
2. perimeter
3. segment
4. point

Answer. 1. area

Question 4. The perimeter of triangle with sides \(\overline{A B}\), \(\overline{B C}\), \(\overline{C A}\)

1. \(\overline{A B}\) + \(\overline{B C}\)
2. \(\overline{A B}\) + \(\overline{B C}\) + \(\overline{C A}\)
3. \(\overline{B C}\) + \(\overline{C A}\)
4. A + B + C

Answer. 2. \(\overline{A B}\) + \(\overline{B C}\) + \(\overline{C A}\)

Question 5. The number of sides of a octagon is

1. 6
2. 7
3. 10
4. 8

Answer. 4. 8

Question 6. If length and breadth of a rectangle is 12 cm and 8 cm respectively, then its perimeter is ….

1. 20 cm
2. 96 cm
3. 40 sq.m.
4. 40 cm

Answer. 4. 40 cm

Question 7. Area of a rectangle

1. l x b
2. 2(l + b)
3. 4s
4. s²

Answer. 1. l x b

Question 8. A = s² is the formula for

1. Area of a rectangle
2. Area of a square
3. Perimeter of a square
4. Perimeter of a rectangle

Answer. 2. Area of a square

Question 9. The sum of all the lengths of a polygon is called ………..

1. area
2. perimeter
3. volume
4. none

Answer. 2. perimeter

Question 10. How many sides are there in a pentagon?

1. 2
2. 9
3. 6
4. 5

Answer. 4. 5

Question 11. In a rectangle l = 3 cm, b = 0.9 cm then A = …… cm²

1. 9
2. 27
3. 2.7
4. 3

Answer. 3. 2.7

Question 12. Side of an equilateral triangle is 3 cm then its perimeter is ………. cm.

1. 3.5
2. 11
3. 12
4. 9

Answer. 4. 9

Question 13. Perimeter of rectangle is …..

1. \(\frac{2}{3}\)(l + b)
2. \(\frac{l+b}{2}\)
3. 2(l + b)
4. \(l+\frac{\mathrm{b}}{2}\)

Answer. 3. 2(l + b)

Question 14. Perimeter of a square is 20 cm then its side is ………. cm.

1. 10
2. 5
3. 4
4. 7

Answer. 2. 5

Question 15. Identify the odd one from the following

1. length
2. breadth
3. area
4. perimeter

Answer. 3. area

Question 16. P = 2(l + b) then l = ……

1. \(\frac{\mathrm{P}}{2}+\mathrm{b}\)
2. \(\frac{P}{2}-l\)
3. \(\frac{P}{2}-b\)
4. \(\frac{P}{2}-2b\)

Answer. 3. \(\frac{P}{2}-b\)

Question 17. Formula to find area of square of side ‘a’ units is ………unit².

1. a
2. 2a
3. \(\frac{a}{2}\)
4. a²

Answer. 4. a²

Question 18. The perimeter of regular hexagon of side 6 cm is ……….. cm.

1. 20
2. 36
3. 15
4. 16

Answer. 2. 36

Question 19. 1 m = ………. cm.

1. 50
2. 60
3. 70
4. 100

Answer. 4. 100

Question 20. The cost of fencing a square park of side 150 m at the rate of ₹ 10 per meter is

1. 6000
2. 5000
3. 1100
4. 1700

Answer. 1. 6000

Question 21. In a rectangle l = 36 m, b = 24 m, then P = …..m.

1. 114
2. 103
3. 120
4. 110

Answer. 3. 120

Question 22. Side of a square is 17 cm then its area is ……… cm².

1. 423
2. 324
3. 189
4. 289

Answer. 4. 2889

Question 23. The area of a rectangle is 1,125 cm2. If its breadth is 25 cm then length = ….. cm.

1. 25
2. 40
3. 15
4. 45

Answer. 4. 45

Question 24. Perimeter of a regular pentagon of side 8 cm is ….. cm.

1. 60
2. 40
3. 80
4. 70

Answer. 2. 40

Question 25. ……… are the simple closed plane figures bounded by line segments.

1. Area
2. Perimeter
3. Square
4. Polygons

Answer. 4. Polygons

Question 26. The perimeter of a triangle is 30 cm. Sum of its two sides is 21 cm, then the length of 3rd side is …….. cm.

1. 13
2. 12
3. 9
4. 11

Answer. 3. 9

Question 27. Area measured in ……….units.

1. square
2. cubic
3. Both A & B
4. none

Answer. 1. square

Question 28. If the perimeter of a square is 48 cm then its side

1. 12 cm
2. 24 cm
3. 6 cm
4. 144 cm

Answer. 1. 12 cm

Question 29. If the area of a square is 144 cm2 then its perimeter is

1. 12 cm
2. 48 cm
3. 24 cm
4. 36 cm

Answer. 2. 48 cm

Question 30. If the side of a square is doubled then its area will be increased by

1. doubled
2. 3 times
3. 4 times
4. None

Answer. 3. 4 times

Question 31. If the side of a square is halved then its area will be

1. same as original area
2. halved
3. 4 times increases
4. \(\frac{1}{4}\) of original area

Answer. 4. \(\frac{1}{4}\) of original area

Question 32. If the length and breadth of rectangle are doubled then its area will be

1. same as original area
2. halved
3. doubled
4. increased by 4 times

Answer. 4. increased by 4 times

Question 33. If the length is doubled and breadth is tripled then its area will be

1. doubled
2. increased by 3 times
3. increased by 6 times
4. same as original area

Answer. 3. increased by 6 times

Question 34. A rectangular plot of land is 240 m by 200 m. The cost of fencing per meter is ₹ 10. What is the cost of fencing the entire field?

1. ₹ 8800
2. ₹ 8000
3. ₹ 4800
4. ₹ 8880

Answer. 1. ₹ 8800

Question 35. A piece of wire is 60 cm long. What will be the length of each side if the string is used to form and equilateral triangle

1. 10 cm
2. 15 cm
3. 20 cm
4. 30 cm

Answer. 3. 20 cm

Question 36. The perimeter of a rectangle whose lengths is ‘l’ meters and breadth is ‘b’ meters is ………… meters.

1. l + b
2. lb
3. 2(l + b)
4. 2l + b

Answer. 3. 2(l + b)

Question 37. The perimeter of a rectangle whose sides are 18 cm and 15 cm is ….. cm.

1. 38
2. 60
3. 66
4. 36

Answer. 3. 66

Question 38. A farmer has to cover three times the perimeter of field. The length is 10 m and the breadth is 8 m then total distance travelled by him is …… m.

1. 108
2. 100
3. 18
4. 36

Answer. 1. 108

Question 39. Perimeter of a square whose side is ‘a’ meters is ………… meters.

1. a⁴
2. 4 + a
3. 2a
4. 4a

Answer. 4. 4a

Question 40. The perimeter of a regular pentagon whose side is 5 cm is …… cm.

1. 28
2. 25
3. 20
4. 29

Answer. 2. 25

Question 41. The area of rectangle whose sides are 3 m and 4 m is …….. sq.m.

1. 12
2. 13
3. 34
4. 7

Answer. 1. 12

Question 42. The area of a square whose side is 4 cm is …….. sq.cm.

1. 4
2. 16
3. 24
4. 8

Answer. 2. 16

Question 43. The area of rectangle is 20 sq.cm and the length is 4 cm then the breadth is ….. cm.

1. 10
2. 4
3. 3
4. 5

Answer. 4. 5

Question 44. The area of rectangle whose measurements are given by length = 3 m and breadth = 40 cm is ……. sq.m.

1. 340
2. 120
3. 1.2
4. 12

Answer. 3. 1.2

Chapter 10 Mensuration Fill in the blanks:

Question 45. The perimeter of a square whose length is 4.5 cm ………..cm

Answer. 18

Question 46. The perimeter of an equilateral triangle is 30 cm then its side is ……..cm

Answer. 10

Question 47. The area of square is 12544 cm² then its side is……cm

Answer. 112

Question 48. The perimeter of a rectangle is 48 cm, its length is 20 cm then its breadth = …………..cm.

Answer. 4

Question 49. The area of adjacent rectangle PQRS is ……………cm².

Answer. 36

Question 50. The cost of fencing a square park of side 250 m. at the rate of 20 per meter is.

Answer. 20,000

Question 51. The area of a square is 144 cm2 then its perimeter is ………..cm

Answer. 48

Question 52. The perimeter of given figure is………cm

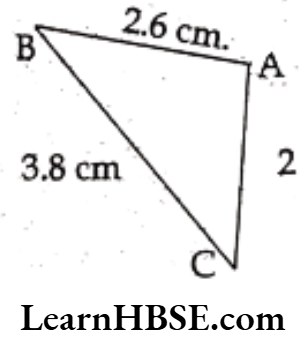
Answer. 8.4

Question 53. The perimeter of a square is 40 cm., then its side is.

Answer. 10 cm.

Question 54. The length of the boundary of closed figure is called its

Answer. perimeter

Question 55. Area of a rectangle is 100 cm2 its length and breadth are equal then its perimeter is………..

Answer. 40 cm.

Question 56. The perimeter of a square is 24 cm., then its area is …….

Answer. 36 cm².

Question 57. The perimeter of a regular hexagon of side 8 cm., is……..

Answer. 48 cm.

Question 58. Which is different among 15 cm., 16 cm., 19 cm.2, 18 cm.

Answer. 19 cm².

Question 59. The side of a square is 6 cm. The length and breadth of rectangle are 7 cm. and 5 cm. respectively. Which has less area?………..

Answer. rectangle

Question 60. Which is different among “length, breadth, side, perimeter, area”………

Answer. area

Question 61. 2(1+b) P is the formula for …………….

Answer. perimeter of a rectangle

Question 62. Which is different among 16 cm², 17 cm², 18 cm², 20 cm² ……

Answer. 18 cm.

Question 63. The sum of the lengths of line segments of the polygon is ………..

Answer. perimeter of the polygon

Question 64. If the area of a rectangular field is 1350 m2 and its length is 50 m then its breadth is ………

Answer. 27 m.

Question 65. If the length of the side of a square is 10 m. Then 100 square mts is its …….

Answer. area

Question 66.

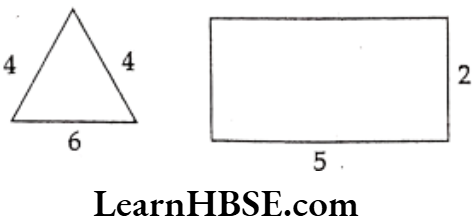
What is the relationship between these shapes?

Answer. perimeters are equal.

Question 67. The amount of surface enclosed by a closed figure is called its ……

Answer. area

Question 68. The perimeter of the regular hexagon is 18 cm then side is ……. cm.

Answer. 3

Question 69. The area of square whose side is 4 cm. is…………………….cm.

Answer. 16

Question 70. The area in square metre of a piece of cloth 1 m 25 cm wide and 2.m long is …….cm².

Answer. 25

Question 71. The perimeter of an equilateral triangle whose side is 4 cm is…….cm.

Answer. 12

Question 72. The perimeter of a triangle whose sides are 3 cm, 4 m and 6 cm is ………….. cm.

Answer. 13

Question 73. The perimeter of the rectangle given in the figure is ………. cm

Answer. 12

Haryana Board Class 6 Maths Solutions For Chapter 10 Mensuration Match The Following:

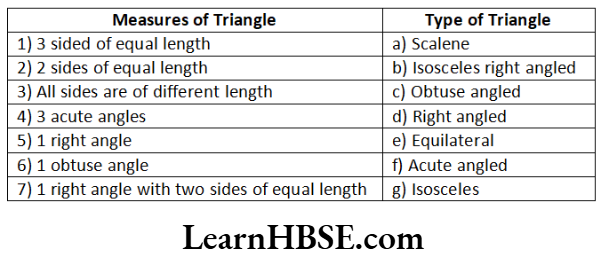
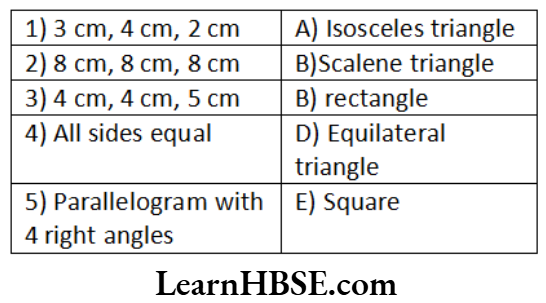
Question 74.

Answer. 1 – D, 2 – A, 3 – B, 4 – F, 5 – E, 6 – C.

Haryana Board Class 6 Maths Solutions For Chapter 9 Data Handling

• ‘Data’ is a collection of numbers gathered to give some information.
• ‘Information’ is either in the form of numbers or words.
• To get a particular information from the given data quickly, the data can be arranged in a tabular form using tally marks.
• Data that has been organised and presented in ‘frequency distribution tables’ can also be represented using ‘pictographs’ and ‘bar graphs’.
• Representation of the data in the form of pictures, objects or parts of objects is called ‘pictograph’ or ‘pictogram’.
• A pictograph uses pictures or symbols to represent the frequency of the data.
• In pictograph the size of all pictures should be the same and should represent the same number of items of the data.
• We use tally marks for recording and organisation of data.
• Representation of data can be done in the following ways (1) Pictographs (2) Bar graphs.
• The pictographs represents the representation of the data through pictures.
• “P.C. Mahalanobis” is known as father of Indian Statistics.

Haryana Board Class 6 Maths Solutions For Chapter 9 Data Handling Exercise 9.1

Question 1. In a Mathematics test, the following marks were obtained by 40 students. Arrange these marks in a table using tally marks.

a) Find how many students obtained marks equal to or more-than 7.

b) How many students obtained marks below 4?

Solution.

a) 5 + 4 + 3 = 12 students obtained marks equal to or more than

7 (7 marks – 5 students, 8 marks – 4 students; 9 marks – 3 students)

b) 3 + 3 + 2 = 8 students obtained marks below 4.

Haryana Board Class 6 Maths Data Handling solutions

Question 2. Following is the choice of sweets of 30 students of Class VI: Ladoo, Barfi, Ladoo, Jalebi, Ladoo, Rasgulla, Jalebi, Ladoo, Barfi, Rasgulla, Ladoo, Jalebi, Jalebi, Rasgulla, Ladoo, Rasgulla, Jalebi, Ladoo, Rasgulla, Ladoo, Ladoo, Barfi, Rasgulla, Rasgulla, Jalebi, Rasgulla, Ladoo, Rasgulla, Jalebi, Ladoo.

a) Arrange the names of sweets in a table using tally marks.

b) Which sweet is preferred by most of the students?

Solution. a)

b) Ladoo is preferred by most of the students.

Question 3. Catherine threw a dice 40 times and noted the number appearing each time as shown below:

Make a table and enter the data using tally marks. Find the numbers that appeared:

a) The minimum number of times.

b) The maximum number of times.

c) Find those numbers that appear an equal number of times.

Solution.

a) Number 4 appeared minimum number of times.

b) Number 5 appeared maximum number of times.

c) Number 1.and 6 appeared equal number of times.

Question 4. Following pictograph shows the number of tractors in five villages.

Observe the pictograph and answer the following questions.

1) Which village has the minimum number of tractors?

Solution. Village D has the minimum number of tractors – 3.

2) Which village has the maximum number of tractors?

Solution. Village C has the maximum number of tractors – 8.

3) How many more tractors village C has as compared to village B ?

Solution. Village C has 8 – 5 = 3 more tractors as compared to village B.

4) What is the total number of tractors in all the five villages?

Solution. Total number of tractors in all the five villages = 6 + 5 + 8 + 3 + 6 = 28.

Question 5. The number of girl students in each class of a co-educational middle school is depicted by the pictograph.

Observe this pictograph and answer the following questions:

a) Which class has the minimum number of girl students?

Solution. Class VIII has the minimum no. of girl students (6).

b) Is the number of girls in class VI less than the number of girls in Class V ?

Solution. No, the number of girls (16) in class VI is not less than the number of girls (10) in class V.

c) How many girls are there in class VII?

Solution. Number of girls in class VII = 3 x 4 = 12.

How to draw a pictograph Class 6 HBSE

Question 6. The sale of electric bulbs on different days of a week is shown below:

Observe the pictograph and answer the following questions:

a) How many bulbs were sold on Friday.

Solution. 14 bulbs were sold on Friday.

b) On which day were maximum number of bulbs sold?

Solution. Maximum bulbs were sold on Sunday.

c) On which of the days same number of bulbs were sold?

Solution. Equal no. of bulbs were sold on Wednesday and Saturday.

d) On which of the days minimum number of bulbs were sold?

Solution. Minimum bulbs were sold on Wednesday and Saturday.

e) If one big carton can hold 9 bulbs. How many cartons were needed in the givenweek?

Solution. No. of bulbs can hold in one big carton = 9

No.of cartons were need = 86 ÷ 9

= 10 (Approx)

Question 7. In a village six fruit merchants sold the following number of fruit baskets in a particular season:

Observe this pictograph and answer the following questions:

a) Which merchant sold the maximum number of baskets?

Solution. Martin sold the maximum number of baskets – 950.

b) How many fruit baskets were sold by Anwar?

Solution. 7 x 100 = 700 fruit baskets were sold by Anwar.

c) The merchants who have sold 600 or more number of baskets are planning to buy a godown for the next season. Can you name them?

Solution. Anwar, Martin and Ranjit Singh are planning to buy a godown for the next season.

Haryana Board Class 6 Maths Solutions For Chapter 9 Data Handling Very Short Answer Questions

Question 1. Give two examples of data in numerical figures.

Solution. Example: 1

The number of students in each class in a school:

Example: 2

The details of number of cricket bats sold in a week:

Question 2. Give two examples of data in words.

Solution. Example: 1

Days of a week

MON, TUE, WED, THU, FRI, SAT, SUN.

Example: 2

Important cities in Andhra Pradesh.

Vijayawada, Guntur, Tirupathi, Visakhapatnam, Machilipatnam, Nellore, Kakinada.

Question 3. Vehicles that crossed a checkpost between 10 AM and 11 AM are as follows:

car, lorry, bus, lorry, auto, lorry, lorry, bus, auto, bike, bus, lorry, lorry, zeep, lorry, bus, zeep, car, bike, bus, car, lorry, bus, lorry, bus, bike, car, zeep, bus, lorry, lorry, bus, car, car, bike, auto.

Represent the data in a frequency distribution table using tally marks.

Solution.

Frequency table and data interpretation Class 6

Question 4. The following pictograph shows the number of students use cycles, in five classes of a school.

Answer the following questions based on the pictograph given above –

1) Which class students have the maximum number of cycles?

2) Which class students have the minimum number of cycles?

3) Which class students have 9 cycles?

4) What is the total number of cycles in all the five classes?

Solution. 1) IX class students have the maximum number of cycles.

2) VI class students have the minimum number of cycles.

3) VIII class students have 9 cycles.

4) Total number of cycles in all the five classes:

VI      5

VII     10

VIII     9

IX       12

X         7

Total   43

Question 5. A book-shelf has books of different subjects. The number of books of each subject is represented as a pictograph given below. Observe them.

Answer the following questions:

1) Which books are more in number?

Solution. Maths

2) Which books are least in number?

Solution. English

3) How many total books are there ?

Solution.

Telugu      4

English     3

Hindi        4

Maths       6

Science     5

Social        4

Total         26

Question 6. 26 students in a class got the following marks in an assignment – 5, 6, 7, 5, 4, 2, 2, 9, 10, 2, 4, 7, 4, 6, 9, 5, 5, 4, 3, 7, 9, 5, 2, 4, 5, 7. The assignment was for 10 marks.

1) Organise the data and represent in the form of a frequency distribution table using tally marks.

2) Find out the marks obtained by maximum number of students.

3) Find out how many students received least marks.

4) How many students got 8 marks?

Solution. 1)

2) Maximum number of students (6) got 5 marks.,

3) Least mark (2) was obtained by 4 students.

4) No student in the class got 8 marks.

How to create a bar graph Class 6 Haryana Board

Question 7. In a class of 25, students like various games. The details are shown in the following pictograph. (No student plays more than one game).

1) How many students play badminton?

2) Which game is played by most number of students ?

3) What is the game in which least number of students are interested?

4) How many students do not play any game?

Solution. 1) 5 students play badminton.

2) Kabaddi is played by most number of students i.e., 7.

3) Tennikoit is played by least number of students i.e., 4.

4) Total number of players = 7 + 4 + 5 + 6 = 22

Number of students in the classroom = 25.

Thus, the number of students who do not play any game = 25 – 22 = 3

Question 8. Give two examples of data in numerical figures.

Solution. 1) The population of Andhra Pradesh in (2011) – 4,96,34,314

2) The cost of I phone 11 pro-1,21,889.

Question 9. Give two examples of data in words.

Solution. 1) The cost of Maruti Brezza [Z x 1] price on road in India – Nine lakh ten thousand rupees only.

2) The population of India according to census 2011 – One hundred and twenty one crore eight lakhs fifty four thousand nine hundred and seventy seven.

Haryana Board Class 6 Maths Solutions For Chapter 9 Data Handling Short Answer Questions

Question 10. A child’s Kiddy bank is opened and the coins collected are in the following denomination.

Represent the data in a frequency distribution table using tally marks.

Solution.

Question 11. The favourite colours of 25 students in a class are given below:

Blue, Red, Green, White, Blue, Green, White, Red, Orange, Green, Blue, White, Blue, Orange, Blue, Blue, White, Red, White, White, Red, Green, Blue, Blue, White.

Write a frequency distribution table using tally marks for the data. Which is the least favourite colour for the students ?

Solution.

colour for the students = 2 (Orange)

Question 12. A TV channel invited a SMS poll on ‘Ban of Liquor’ giving options:-

A – Complete ban

B – Partial ban

C – Continue sales

They received the following SMS, in the first hour-

Represent the data in a frequency distribution table using tally marks.

Solution.

Question 13. The number of wrist watches manufactured by a factory in a week are as follows:

Represent the data using a pictograph. Choose a suitable scale.

Solution. = 50 watches.

Question 14. Votes polled for various candidates in a sarpanch election are shown below, against their symbols in the following table.

Represent the data using a pictograph. Choose a suitable scale.

Answer the following questions:

1) Which symbol got least votes?

2) Which symbol candidate won in the election?

Solution. Each represents 50 votes

1) Watch symbol got least votes.

2) Pot symbol candidate won in the election.

Question 15. The sale of television sets of different companies on a day is shown in the pictograph given below. Scale: = 5 televisions

Answer the following questions:

1) How many TVs of company A were sold?

2) Which company’s TVs are people more crazy about?

3) Which company sold 15 TV sets?

4) Which company had the least sale?

Solution. 1) Number of TV’s sold by company A = 5 x 5 = 25

2) People more crazy about the TV company ‘C’.

3) Company ‘E’ sold 15 TV sets.

4) Company ‘D’ sold least sale.

Haryana Board Class 6 Maths Solutions For Chapter 9 Data Handling Long Answer Questions

Question 16. Given below are the ages of 20 Students of Class VI in a School.

13, 10, 11, 12, 10, 11, 11, 13, 12, 11, 10, 11, 12, 11, 13, 11, 10, 13, 10, 12

1) Organise the data and represent in the form of a frequency distribution table using tally marks.

Solution.

2) Find out the age having more number of students

Solution. More number of students having the age is 11 years.

3) How many students are there in 10 Years age?

Solution. 5 students

4) Find out number of students who are having more age?

Solution. Number of students who are having more age 13 years is 4.

Question 17. A die was thrown 30 times and following scores were obtained

5 3 4 6 2 3

6 2 2 3 15

2 5 4 6 2 1

4 5 1 6 2 1

3 1 3 3 4 6

Word problems on pictographs and bar graphs Class 6

1) Prepare a frequency table of the scores.

Solution.

2) Which number obtained more times?

Solution. The numbers 2 and 3 obtained more times ie., 6.

3) How many times was a score greater than 4 obtained?

Solution. The number of times a score greater than 4 obtained was 4 + 5 = 9

4) Find the total number of times an odd number obtained.

Solution. Total number of times an odd number obtained is = 5 + 6 + 4

= 15 [1, 3 and 5 are faces of a dice]

Haryana Board Class 6 Maths Solutions For Chapter 9 Data Handling Objective Type Questions

Choose the correct answer:

Question 1. The information collected in terms of numbers

theorem

data

mean

range

Answer. 2. data

Question 2. Representing the data in terms of pictures is

Bar graphs

Bar charts

Pictographs

Pie charts

Answer. 3. Pictographs

Question 3. While drawing pictures in a pictograph all ………… must be equal.

lengths

sizes

breadths

bases

Answer. 2. sizes

Question 4. || indicates ….

7

6

3

5

Answer. 1. 7

Question 5. If a * represents 3 cars, how many * are required to indicate 18 cars?

3

6

8

12

Answer. 2. 6

Question 6. If 6 cm represent 9 lakh people then the scale is ………..

1 cm = 1,50,000

2 cm = 1,00,000

1 cm = 2,00,000

1 cm = 1,20,000

Answer. 1. 1 cm = 1,50,000

Question 7. In a data maximum value = 30 and the minimum value is 10. Then the range is

31

12

20

16

Answer. 3. 20

Question 8. 13 can be represented by tally marks as

|||

||

|

Answer. 2. |||

Question 9. According to the scale \(\frac{1}{2}\) cm = 15 students then 45 students = …… cm

8

4

7

\(\frac{3}{2}\)

Answer. 4. \(\frac{3}{2}\)

Question 10. ………. are used in preparing frequency table

Symbols

Tally marks

Data

Scale

Answer. 2. Tally marks

Data Handling examples for Class 6 HBSE Maths

Question 11. Which of the following indicates ‘5’

|||||

|||

Answer. 2. Diagram

Question 12. Average of 1, 2, 3 is

1. 2
2. 3
3. 8
4. 3.5

Answer. 1. 2

Question 13. Statement – a: A table showing the frequency or count of various items is called a frequency distribution.

Statement – b: To get a particular information from the given data quickly, the data can be arranged in a tabular form using tally marks.

1. both a & b are true
2. a is true b is false
3. a is false, b is true
4. both a & b are false

Answer. 1. both a & b are true

Question 14. Father of Indian Statistics

1. Ramanujan
2. Aryabhata
3. P.C.Mahalanobis
4. Bhaskaracharya

Answer. 3. P.C.Mahalanobis

Question 15. If represents = 10 books then represent = …….books.

1. 10
2. 20
3. 30
4. 40

Answer. 4. 40

Answer the questions [16-19] from the information given below.

Question 16. How many marks obtained by maximum number of students?

1. 5
2. 6
3. 2
4. 10

Answer. 1. 5

Question 17. How many students received least marks?

1. 1
2. 2
3. 4
4. 10

Answer. 3. 4

Question 18. How many students got 8 marks?

1. 1
2. 4
3. 21
4. 0

Answer. 4. 0

Question 19. How many students got more than 8 marks?

1. 3
2. 4
3. 8
4. 21

Answer. 2. 4

Question 20. If represents 5 eggs, then how many eggs do represent?

1. 20
2. 25
3. 100
4. 30

Answer. 2. 25

Question 21. If represents 5 balloons, then the number of symbols to be drawn to represent 70 balloons is

1. 12
2. 10
3. 15
4. 14

Answer. 4. 14

Question 22. The number of members in 20 families in a village is given as 6, 8, 6, 3, 2, 5, 7, 8, 6, 5, 5, 7, 7, 8, 6, 6, 7, 7, 6, 5.

How many families are of the largest size?

1. 4
2. 3
3. 5
4. 6

Answer. 2. 3

Question 23. The number of times an observation occurs is called

1. frequency
2. data
3. tallymarks
4. none

Answer. 1. frequency

Haryana Board Class 6 Maths Solutions For Chapter 9 Data Handling Fill in the blanks:

Question 24. Diagram represents ……

Answer. 5

Question 25. 1 + 3 + 4 + 5 + 6 + 7 + 8 + 10 = ……….

Answer. 44

Question 26. ……………… collection of numbers gathered to give some information.

Answer. Data

Question 27. Average of -2, -1, 0, 1, 2, … ………….

Answer. 0

Question 28. According to a scale \(\frac{1}{2}\) cm = 20 students then 60 students

Answer. 3/2

Question 29. Range of first 10 whole numbers is ………

Answer. 9

Question 30. Range of first 100 even natural numbers is = …….

Answer. 98

Question 31. Show 12 as tally mark…………….

Answer. ||

Question 32. Collection of certain information is called …….

Answer. data

Question 33. Representing the data in the form of pictures is called ………

Answer. pictograph

Question 34. If Diagram represents 150 then Diagram represent …….

Answer. 750

Question 35. If 100 books = Diagram then 150 books are represented by ……….

Answer. ▢▢ ▢

Question 36. The tally marks ||| represent ………..

Answer. 13

Question 37. Which are used in preparing frequency table are ……..

Answer. Tally marks

Question 38. The tally marks to represent 16……………..

Answer. |

Haryana Board Class 6 Maths Solutions For  Chapter 6 Integers

• The collection of all positive numbers, zero and negative numbers together are called ‘Integers’.
  The set of Integers is denoted by the symbol Z. Z = {………….. -4, -3, -2, -1, 0, 1, 2, 3, 4 …}
• The number without any sign is considered positive number only.
  Eg: 3 is considered + 3
• Brahmagupta (598 AD-670 AD) first used a special sign (-) for negative numbers and stated the rules for dealing with positive and negative quantities.
• The letter “Z” was first used by the Germans because the word for Integers in the Ger- man language is “Zehlen”, which means “Number”.
• Natural numbers, (1,2,3,4,…) are also called positive integers and Whole numbers. {0,1,2,3,4,…) are also called non-negative integers.
  Negative numbers are important to represent just opposite numbers for positive numbers.
• Every integer can be represented on a number line horizontally or vertically.
• Addition and subtraction of integers can be done on number line.
• Every negative integer is always lesser than zero.
• The smallest and the biggest positive integers are +1 and positive infinite (+∞).
• The smallest and the biggest negative integers are negative infinite (-∞) and -1
• The sum of two negative integers is always a negative integer. Eg: -2 + (-3) = -5
• The sum of two positive integers is always a positive integer. Eg: 5 + 7 = 12
• The sum of two integers, one of which is positive and the other is negative, then the sum may be either positive, negative or zero.
  Eg: 12 + (-9) = 3;-12 + 9 = -3;-3 + 3 = 0
• For any integer a, -(-a) = a
• We add the opposite of an integer (additive inverse) to an integer in subtraction.
• Integers are widely used in our daily life i.e., business, engineering, games, temperatures, medicine etc……
• Integers are closed under addition and sub- traction.
• Integers are commutative and associative under addition.
• Integers are not commutative and associative under subtraction.
• We use negative numbers to represent debit, temperature below the 0°C, past periods of time depth below sea level.
• Number Line:

• The numbers on the left side of zero (i.e., less than zero) are called ‘negative numbers’.
• The numbers on the right side of zero (i.e., greater than zero) are called ‘positive numbers’.
• We can show the addition and subtraction of integers on the number line.
• ‘O’ is neither positive nor negative.
• Any two distinct numbers that give zero when added to each other are additive inverse of each other.
  Eg. : 3 and -3
  3 + (-3) = 0
• The subtraction of integers is the same as the addition of their additive inverse.
  Eg. The additive inverse of 7 is -7
  The additive inverse of -8 is 8
• Numbers with a negtative sign are called negative numbers. They are less than zero.
• If we add ‘1’ (one) to a given number we get successor.
• If we subtract ‘one’ from a given number we get predecessor.
• If we move right side of a given number on a number line the value of the number increases and to the left the value decreases.
• If we add a positive number and a negative number we must do subtraction and put the sign of the bigger number.
• The addition of two integers is zero then each one is called additive inverse of the other.

Suppose David and Mohan have started walking from zero position in opposite directions. Let the steps to the right of zero be represented by ‘+’ sign and to the left of zero represented by “” sign. If Mohan moves 5 steps to the right of zero it can be represented as +5 and if David moves 5 steps to the left of zero it can be represented as -5. Now represent the following positions with +or – sign:

a) 8 steps to the left of zero.

Answer. -8

b) 7 steps to the right of zero.

Answer. +7

c) 11 steps to the right of zero.

Answer. +11

d) 6 steps to the left of zero.

Answer. -6

Write the succeeding number of the following:

Write the preceeding number of the following:

Write the following numbers with appropriate signs:

a. 100 m below sea level.

Solution. -100 m

b. 25°C above 0°C temperature.

Solution. + 25°C

c. 15°C below 0°C temperature.

Solution. -15°C.

d. Five numbers less than 0.

Solution. -1, -2, -3, -4, -5

Mark 3, 7,-4,-8,- 1 and 3 on the number line.

Solution.

Compare the following pairs of numbers using > or <.

0 _ 8

-1 _ -15

5 _ -5

11 _ 15

0 _ 6

– 20 _ 2

Solution.

0 > 8

-1 > -15

5 > -5

11 < 15

0 < 6

-20 < 2

Haryana Board Class 6 Maths Solutions For  Chapter 6 Integers Exercise – 6.1

Question 1. Write the opposites of the following:

a) Increase in weight

b) 30 km north

c) 80 m east

d) Loss of Rs. 700

e) 100 m above sea level

Solution. a) decrease in weight

b) 30 km south

c) 80 m west

d) Profit of Rs. 700

e) 100 m below sea level

Haryana Board Class 6 Maths Integers solutions

Question 2. Represent the following numbers as integers with appropriate signs.

a) An aeroplane is flying at a height, two thousand metre above the ground.

Solution. +2000 metre

b) A submarine is moving at a depth, eight hundred metre below the sea level.

Solution. -800 metere

c) A deposit of rupees two hundred.

Solution. +Rs. 200

d) Withdrawal of rupees seven hundred.

Solution. -Rs. 700

Question 3. Represent the following numbers on a number line.

a) +5

b) -10

c) +8

d) -1

e) -6

Addition and subtraction of integers Class 6 HBSE

Question 4. Adjacent figure is a vertical number line, representing integers. Observe it and locate the following points:

a. If the point D is + 8, then which point is -8?

Solution. Point F.

b. Is point G is a negative integer or a positive integer?

Solution. It is a negative integer.

c. Write integers for points B and E.

Solution. Integer for point B = +4

Integer for point E = -10.

d. Which point marked on this number line has the least value?

Solution. Point E.

e. Arrange all the points in decreasing order of value.

Solution. D, C, B, A, O, H, G, F, E.

Question 5. Following is the list of temperatures of five places in India, on a particular day of the

a) Write the temperatures of these places in the form of integers in blank column.

Solution.

b) Following is the number line representing the temperature in degree celsius.

Plot the name of the city against its temperature.

c) Which is the coolest place?

Solution. Siachin is the coolest place.

d) Write the names of the places where temperatures are above 10° C.

Solution. Delhi and Ahmedabad.

Question 6. In each of the following pairs, which number is to the right of the other on the number line?

a) 2,9

Solution. The number 9 is to the right of the number 2.

b) -3, -8

Solution. The number -3 is to the right of the number -8.

c) 0,-1

Solution. The number ‘0’(zero) is to the right of the number -1.

d) -11, 10

Solution. The number 10 is to the right of the number -11.

e) -6,6

Solution. The number 6 is to the right of the number -6.

f) 1, -100

Solution. The number 1 is to the right of the

Multiplication and division of integers Class 6

Question 7. Write all the integers between the given pairs (write them in the increasing or

a. 0 and -7.

Solution. -6,-5,-4,-3,-2 and -1.

b. -4 and 4.

Solution. -3, -2, -1, 0, 1, 2 and 3.

C. -8 and -15.

Solution. -14,13,12,-11,-10 and -9.

d. 30 and -23.

Solution. -29,-28,-27,-26,-25 and -24.

Question 8. a. Write four negative integers greater than 20.

Solution. 19, -18,-17 and – 16..

b. Write four negative integers less than -10.

Solution. 11, 12, 13, and – 14.

Question 9. For the following statements, write True (T) or False (F). If the statement is false, correct the statement.

a. -8 is to the right of -10 on a number line.

Solution. True (T)

b. -100 is to the right of -50 on a number line.

Solution. False (F)

c. Smallest negative integer is -1.

Solution. False (F)

d. -26 is greater than -25.

Solution. False (F)

Question 10. Draw a number line and answer the following:

a. Which number will we reach if we move 4 numbers to the right of – 2?

Solution. We reach the number ‘2’.

b. Which number will we reach if we move 5 numbers to the left of 1?

Solution. We reach the number – 4.

c. If we are at 8 on the number line, in which direction should we move to reach – 13?

Solution. We should move in the left direction.

d. If we are at 6 on the number line, in which direction should we move to reach – 1?

Solution. We should move in the right direction.

Question 11. Draw a figure on the ground in the form of a horizontal number line as shown below. Frame questions as given in the said example and ask your friends.

1) Which is greater (-2) or (-1)?

Solution. 1.

2) Which is smaller among – 6 and 3?

Solution. -6.

3) Which is the nearest positive integer to zero ?

Solution. 1.

4) Which integer is neither positive nor negative ?

Solution. ‘O’ is neither positive nor negative.

5) How many negative numbers you will find on left side of zero?

Solution. Infinite

6) Write three integers greater than -2.

Solution. -1,0,1.

7) Write five integers lesser than -1.

Solution. -2,-3,-4,-5, -6.

8) Which is the nearest positive integer to -1?

Solution. +1.

Integer number line Class 6 Haryana Board

Question 12. Take two different coloured buttons like white and black. Let us denote one white button by (+1) and one black button by (-1). A pair of one white button (+1) and black button (-1) will denoted zero i.e. [1 + (-1) = 0]

In the following table, integers are shown with the help of coloured buttons.

Let us perform additions with the help of the coloured buttons. Observe the following table and complete it.

Question 13. Find the answers of the following additions:

a. (-11)+(-12)

Solution. (-11) + (-12)

= -11 – 12 = -23.

b. (+10) + (+4)

Solution. 10 + 4 = 14.

c. (32) + (-25)

Solution. -32 + (-25)

= -32 – 25 = -57.

d. (+23) + (+40)

Solution. 23 + 40 = 63.

Question 14. Find the solution of the following:

a. (-7) + (+8)

Solution. -7 + (+8)

= -7 + 7 + 1 = 1.

b. (-9) + (+13)

Solution. (-9) + (+13)

= -9 + 9 + 4 = 4.

c. (+7) + (-10)

Solution. +7 + (-10) = +7 – 10

[∴ -10 = -7 – 3]

= 7 – 7 – 3 = -3.

d. (+12) + (-7)

Solution. (+12) + (-7) = 12 – 7

[∴ 12 = 5 + 7]

= 5 + 7 – 7 = 5.

Question 15. Find the solution of the following additions using a number line:

a) (-2) + 6

Solution.

∴ 2 + 6 = 4

b. (-6) + 2

Solution.

∴ -6 + 2 = -4

Question 16. Make two such questions and solve them using the number line.

Solution. 1) (-5) + 3

∴ 5 + 3 = -2

2) -3 + 5

Question 17. Find the solution of the following without using number line.

a) (+7) + (-11)

Solution. 7 – 11 = -4

b) (-13) + (+10)

Solution. 13 + 10 = -3.

c) (-7)+(+9)

Solution. -7 + 9 = 2.

d) (+10)+(-5)

Solution. 10 – 5 = 5.

Make five such questions and solve them.

Question 18. Find the solution of (-7) + (+3) without using the number line.

Solution. (-7) + (+3) = (-4)

Question 2. Find the solution of (+15) + (-9) without using the number line.

Solution. (+15) + (-9) = (+6)

Question 3. Find the solution of (-20) + (+20) without using the number line.

Solution. (-20) + (+20) = 0

Question 4. Find the solution of (+11) + (-11) without using the number line.

Solution. (11) + (-11) = 0

Question 5. Find the solution of (-5) + (+7) without using the number line.

Solution. (-5) + (+7) = (+2)

Haryana Board Class 6 Maths Solutions For  Chapter 6 Integers Exercise 6.2

Question 1. Using the number line write the integer which is:

a) 3 more than 5.

Solution.

∴ 3 more than 5 is 8.

Word problems on integers for Class 6 HBSE

b) 5 more than -5.

Solution.

∴ 5 more than -5 is ‘0’.

c) 6 less than 2.

Solution.

∴ 6 less than 2 is -4.

d) 3 less than -2.

Solution.

∴ 3 less than 2 is -5.

Question 2. Use number line and add the following integers :

a) 9 + (-6)

Solution.

∴ 9 – 6 = 3

b) 5 + (-11)

Solution.

∴ 5 – 11 = -6.

c) (-1) + (-7)

Solution.

∴ -1 – 7 = -8.

d) -5 + 10

Solution.

∴ -5 + 10 =5 .

e) (-1) + (-2) + (-3)

Solution.

∴ -1 – 2 – 3 = -6.

f) (-2) + 8 + (-4)

Solution.

∴ – 2 + 8 – 4 = 8 – 6 = 2.

Question 3. Add without using number line:

a) 11 + (-7).

Solution. 11 + (-7)

= 11 – 7

= 4 + 7 – 7 [∴ 11 = 4 + 7]

= 4 + 0 = 4

b) (-13) + (+18)

Solution. (-13) + (+18)

= -13 + 18

= -13 + 13 + 5

[∴ 18 = 13 + 5]

= 0 + 5

= 5

c) (-10) + (+19)

Solution. (-10) + (+19) = -10 + 19

= -10 + 10 + 9

= 0 + 9

= 9

d) (-250) + (+150)

Solution. -250 + 150 = -150 – 100 + 150

[∴ – 250 = -150 – 100]

= -150 + 150 – 100

= 0 – 100

= -100

e) (-380) + (-270)

Solution. (-380) + (-270)

= -380 – 270

= -650

f) (-217)+(-100)

Solution. (-217) + (-100)

= -217 – 100

= -317

Question 4. Find the sum of:

a) 137 and -354

Solution. 137 + (-354) = 137 – 137 – 217

[∴ -354 = -137 – 127]

= 0 – 217

= – 217

b) -52 and 52

Solution. -52 + 52 = 0

c) -312, 39 and 192.

Solution. -312, 39 and 192.

= -300 – 12 + 39 + 192

[∴ -312 – 300 – 12]

= -300 – 12 + 39 + 180 + 12

= -300 + 219 – 81.

d) -50 – 200 + 300

Solution. -50 – 200 + 300

= -250 + 300

= -250 + 250 + 50

[∴ 300 = 250 + 50]

= +50

= 50

Question 5. Find the sum?

a) (-7) + (-9) + 4 + 16

Solution. (-7) + (-9) + 4 + 16

= -16 + 20

= -16 + 16 + 4 (20 = 16 + 4)

= 0 + 4 – 4

b) (37) + (-2) + (-65) + (-8)

Solution. 37 + (-2) + (-65) + (-8) = 37 – 75

= 37 – 75

= -38

Chapter 6 Integers Exercise 6.3

Question 1. Find:

a) 35-(20)

Solution. 35 – 20 = 15 + 20 – 20 (35 = 15 + 20)

= 15 + 0

= 15

b) 72 – (90)

Solution. 72 – 90

= 72 – 72 – 18 [∴ -90 = -72 – 18]

=0 – 18

= -18

c) (-15) – (-18)

Solution. -15 – (-18)

= -15 + 18

= -15 + 15 + 3 [∴ 18 = 15 + 3]

= 0 + 3

= 3

d) (-20)-(13)

Solution. -20 – 13

= -33

e) 23 (12)

Solution. 23 – (-12)

= 23 + 12 = 35 [∴ – x – = +]

f)(-32) – (-40)

Solution. (-32) – (-40)

= -32 + 40

= -32 + 32 + 8

[∴ 40 = 32 + 8]

= 0 + 8

= 8.

Question 2. Fill in the blanks with >, < or = sign.

a) (-3)+(-6) ____ (-3)-(-6)

Solution. L.H.S. = -3 – 6 = -9

R.H.S. = -3 – (-6)

= -3 + 6 = 3

∴ (-3) + (-6) < (-3) – (-6)

b) (-21) – (-10) ____ (31) + (-11)

Solution. L.H.S. = -21 – (-10) = -21 + 10 = -11

R.H.S. = -31 + (-11) = -31 – 11 = -42

= (-21) – (-10) > (-31) + (-11)

c) (45)-(-11) ____ 57 + (-4).

Solution. L.H.S. = 45 – (-11) = 45 + 11 = 56

R.H.S. = 57 + (-4) = 57 – 4 = 53

= 45 – (-11) > 57 + (-4)

d) (-25)-(-42) ____ (-42)-(-25)

Solution. L.H.S. = -25 – (-42) = -25 + 42.

= -25 + 25 + 17

= 0 + 17 = 17

R.H.S. = (-42)-(-25) = -42 + 25

= -17 – 25 + 25

= -17 – 0 = -17

∴ (-25) – (-42) > (-42) – (-25)

Question 3. Fill in the blanks:

a) (-8) + ____ = 0

Solution. (-8) + 8= 0

b) 13 + ____ = 0

Solution. 13 + (-13) = 0

c) 12 + (-12) = ____

Solution. 12 + (-12) = 0

d) (-4) + ____ = -12

Solution. (-4) + (-8) = -12.

e) ____ -15 = -10

Solution. (+5) – 15 – 10

Question 4. Find:

a) (-7) – 8 – (-25)

Solution. (-7) -8 -(-25) = 7 – 8 + 25

= -7 – 8 + 7 + 18 [∴ 25 = 7 + 18]

= -8 + 18

= -8 + 8 + 10

= 0 + 10 = 10

b) (-13) + 32 – 8 – 1

Solution. (-13) + 32 – 8 – 1

= -13 + 32 – 9

= -13 + 23 + 9 – 9 [∴ 32 = 23 + 9]

= -13 + 23

= -13 + 13 + 10

= 0 + 10

= 10

c) (-7)+(-8)+(-90)

Solution. (-7) + (-8) + (-90)

= -7 – 8 – 90

= -15 – 90

= -105

d) 50 (-40)-(-2).

Solution. 50 – (-40) – (-2)

50 + 40 + 2 = 90 + 2

= 92

Haryana Board Class 6 Maths Solutions For  Chapter 6 Integers Very Short Answer Questions

Question 1. Put appropriate symbol > or < in the boxes given between the two integers.

1) – 1………. 0

Solution. -1 < 0

2) -3 …….. -7

Solution. -3 > -7

3)-10 ……. +10

Solution. -10 < +10

Question 2. The temperature recorded in Shimla is -4° c and in Kufri is -6°c on the same day. Which place is colder on that day? Why?

Solution. Temperature recorded in Shimla = -4°C;

Kufri = -6°C

Comparing these: -6 < -4

∴ Kufri is colder than Shimla.

Question 3. Find the sum of:

1) 120 and -274

Solution. The sum of 120 and -274 is

= 120 + (-274)

= -154

2) -68 and 28

Solution. The sum of -68 and 28 is

= -68 + 28

= -40

Question 4. Simplify

1) (-6) + (-10) + 5 + 17

Solution. -6 + (-10) + 5 + 17 = -16 + 22

= 6

2) 30 + (-30) = (-60) + (-18)

Solution. 30 + (-30) + (-60) + (-18)

= [30+(-30)] + [(-60)+(-18)]

= 0 + (-78)

= -78

Question 5. Fill in boxes with <, > or = sign.

1) (-4) + (-5) ____ (-5) – (-4)

Solution.-9 < -1

2) (-16)-(-23) ____ (-6) + (-12)

Solution. 7 > -18

3) 44-(-10) ____ 47+ (-3)

Solution. 54 > 44

Question 6. Fill in the blanks:

1) (-13) + …… = 0

Solution. (-13) + 13 = 0

2) (-16) + 16 =

Solution. (-16) + 16 = 0

3) (-5) + …………. = -14

Solution. (-5) + (-9) = -14

4) ……..+ (2 – 16) = -22

Solution. -8 + (2 – 16) = -22 [∴ 2 – 16 = -14]

Question 7. Arrange the following integers in ascending order and descending order. -1000, 10,-1,-100, 0, 1000, 1, -10

Solution. Ascending order: -1000, -100, -10, -1, 0, 10, 1000 (From smallest to greatest)

Descending order: 1000, 10, 0, 1-, -10, – 100,-1000 (From greatest to smallest)

Question 8. The temperature in Nainital is -5° C and in Shimla is -10° C. In which place is the temperature higher ?

Solution.

The temperature in Nainital is -5°C and temperature in Shimla is -10°C – 5°C is greaterthan -10°C.

∴ The temperature in Nainital is higher than the temperature in Shimla.

Question 9. Simplify (-7)+(-12)+5+12

Solution. (-7) + (-12) + 5 + 12 = [-7 – 12] + [5 + 12]

= -19 + 17

= -2

Question 10. Find 25 + (-21) + (-20) + 17 + (-1).

Solution. 25 + (-21) + (-20) + 17 + (-1)

= 25 + 17 + [-21 – 20 – 1]

= 42 + [-42]

= 42 – 42 = 0

Haryana Board Class 6 Maths Solutions For  Chapter 6 Integers Short Answer Questions

Question 11. Represent the integers on a number line as given below.

1) Integers lie between -7 and -2.

2) Integers lie between -2 and 5.

Solution. 1) The integers lie between -7 and -2 are -6, -5, -4, -3

2) The integers lie between -2 and 5 are -1, 0, 1, 2, 3, 4

Question 12. Write the following integers in increasing and decreasing order:

1) -7,5,-3

Solution. Increasing order: -7,-3,5

Decreasing order: 5, -3, -7

2) -1,3,0

Solution. Increasing order: -1,0,3

Decreasing order: 3, 0, -1

3) 1,3, -6

Solution. Increasing order: -6, 1, 3

Decreasing order: 3, 1, -6

4) -5, -3, -1

Solution. Increasing order: -5, -3, -1

Decreasing order: -1, -3, -5

Question 13. Write True or False, Correct those that are false:

1) Zero is on the right of -3

Solution. True

2) -12 and +12 represent the same integer on the number line.

Solution. False; Correct answer : -12 is a negative integer and +12 is a positive integer.

3) Every positive integer is greater than zero.

Solution. True

4) (-100) > (+100)

Solution. False; Correct answer: -100 < +100.

Question 14. Find the value of the following using a numberline.

1) (-3) + 5

2) (-5) + 3

Make your own two new questions and solve them using the number line.

Solution. 1) (-3) + 5

First move 3 steps to the left of 0 reach – 3 and then from that point we move 5 steps to the right. We reach the number.

∴ (-3) + 5 = 2

Solution. 2) (-5) + 3

First move 5 steps to the left of 0 reach – 5 and then from that point we move 3 steps to the right. We reach the number – 2.

∴ (-5) + 3 = -2.

Question 15. Add without using number line.

1) 10 + (-3)

2) (-10) + (+16)

3) (-8) + (+8)

Solution.

1) 10+ (-3)

= (7 + 3) + (-3)

= 7 + [3+(-3)]

= 7 + 0 = 7

2) (-10) + (+16)

= (-10) + 10 + 6

= [-10 + 10] + 6

= 0 + 6 = 6

3) (-8) + (+8) = 0

Chapter 6 Integers Long Answer Questions

Question 16. Find all integers which lie between the given two integers. Represent them on number line.

1) -1 and 1

2) -5 and 0

3) -6 and -8

4) 0 and -3

1) -1 and 1

Solution. The integer between -1 and 1 is 0.

2) -5 and 0

Solution. The integers between -5 and 0 are -4, -3, -2, -1.

3) -6 and -8

Solution. The integer between -6 and -8 is -7.

4) 0 and -3

Solution. The integers between 0 and -3 are -1, -2

Properties of integers Class 6 HBSE Maths

Question 17. Add the following integers using number line.

(1) 7 + (-6)

(2) (-8) + (-2)

(3) (-6)+(-5)+(+2)

1) 7 + (-6)

Solution.

First move to the right of 0 by 7 steps to each 7, then move 6 steps to the left of 7 we reach 1.

∴ 7 + (-6) = 1

2) (-8) + (-2)

Solution.

First move to the left of 0 by 8 steps to reach -8, then again move 2 steps to the left of -8 we reach -10.

3) (-6)+(-5) + (+2)

Solution.

First move to the left of 0 by 6 steps to reach – 6.

Again move 5 steps to the left of -6 we reach -11.

Now move 2 steps to the right of -11 we reach -9.

∴ (-6) + (-5) + (+2) = -9.

Question 18. In a quiz competition,where negative score for wrong answer is taken,Team A scored +10, -10, 0, -10, 10,-10 and Team B scored 10,10, -10,0,0,10 in 6 rounds successively. Which team wins the competition? How?

Solution. In a quiz, the score made by team A are +10, -10, 0, -10, 10, -10-

The total score made by team A

= 10 + (-10) + 0 + (-10) + 10 + (-10) = -10

The score made by team B are 10, 10, -10, 0, 0, 10

The total score made by team B

= 10 + 10 + (-10) + 0 + 0 + 10 = 20
Team B scored more than team A.

∴ Team B wins the quiz competition.

Question 19. Find the values of (1) (-3)+(-8)+(-5); (2) (-1)+7+ (-3) using number line.

1) (-3) + (-8) + (-5)

Solution.

First move to the left of 0 by 3 steps to reach – 3.

Again move 8 steps to the left of -3 we reach -11.

Now move 5 steps to the left of -11 we reach -16.

∴ (-3) + (-8) + (-5) = -16

2) (-1) + (7) + (-3)

Solution.

First move to the left of 0 by 1 steps to reach – 1.

Again move 7 steps to the right of -1 we reach 6.

Now move 3 steps to the left of -6 we reach 3.

∴ (-1) + 7 + (-3) = 3

Question 20. Represent the following statements using signs of integers :

1) An aeroplane is flying at a height of 3000 meters.

Solution. +3000 meters (height)

2) The fish is 10 meters below the water surface.

Solution. -10 meters (depth)

3) The temperature in Vijayawada is 35°C above 0°C.

Solution. +35° C (+ more),

4) Water freezes at 0°C temperature.

Solution. 0° C (neither ‘+’ nor ‘-‘)

5) The average temperature at the mount Everest in January is 36°C below zero degree.

Solution. -36° C (less)

6) The submarine is 500 meters below the surface of the sea.

Solution. -500 meters (below)

7) The average temperature at Darjeeling in July is 19°C below zero degree.

Solution. -19° C (less)

8) The average low temperature in Vishakapatnam during January is 18°C.

Solution. -18° C (more)

Haryana Board Class 6 Maths Solutions For  Chapter 6 Integers Objective Type Questions

Choose the correct answer :

Question 1. Set of integers is denoted by

1. N
2. Z
3. W
4. Q

Answer. 2. Z

Question 2. Write all the integers lie between 0 and -3

1. 1, 2
2. -4, -5
3. -1, -2
4. 4, 5

Answer. 3. -1, -2

Question 3. The sum of two negative integers is always

1. negative
2. positive
3. 0
4. None of these

Answer. 1. negative

Question 4. The sum of two integers one of which is positive and the other is negative then the sum may be

1. positive
2. negative
3. zero
4. any one of the above

Answer. 4. any one of the above

Question 5. Subtract +5 from (-5)

1. 0
2. 10
3. -10
4. 5

Answer. 3. -10

Question 6. 18 – 18 + 1 = …..

1. -4
2. -1
3. 3
4. 1

Answer. 4. 1

Question 7. -2 … 1

1. =
2. ⊥
3. <
4. >

Answer. 3. <

Question 8. Sum of 10 and -16 is …….

1. -6
2. 6
3. 12
4. -26

Answer. 1. -6

Question 9. Choose the correct matching:

1. 1 – d, 2 – b, 3 – c, 4 – a
2. 1 – b, 2 – d, 3 – a, 4 – c
3. 1 – b, 2 – d, 3 – c, 4 – a
4. 1 – a, 2 – d, 3 – b, 4 – c

Answer. 2. 1 – b, 2 – d, 3 – a, 4 – c

Question 10. The lest negative integer is

1. 1
2. -1
3. -7
4. does not exist

Answer. 4. does not exist

Question 11. Subract -8 from 8

1. 19
2. 0
3. 11
4. 16

Answer. 4. 16

Question 12. -4 – 4 + (-4) + (-4) =

1. -16
2. -12
3. 13
4. 84

Answer. 1. -16

Question 13. Additive inver of 7 – 3 is

1. 4
2. -4
3. 8
4. -7

Answer. 2. -4

Question 14. -20 – 82 = …

1. 111
2. -200
3. 100
4. -102

Answer. 4. -102

Question 15. Integer between -1 and + 1

1. 1
2. 2
3. 0
4. 4

Answer. 3. 0

Question 16. -131 + ……… = 0

1. -13
2. 131
3. 117
4. 814

Answer. 2. 131

Question 17. 38 – (-40) = …….

1. 31
2. 2
3. 16
4. 78

Answer. 4. 78

Question 18. -3 – (-3) = ………

1. -9
2. 0
3. 1
4. -2

Answer. 2. 0

Question 19. -8 + (-9) + (+17) =

1. -3
2. 11
3. -1
4. 0

Answer. 4. 0

Question 20. The smallest among -7, 0, 1, 5 is

1. 1
2. 5
3. 0
4. -7

Answer. 4. -7

Question 21. The greater negative integer in the following is

1. -1
2. -4
3. -7
4. -6

Answer. 1. -1

Question 22. …… is neither positive nor negative.

1. 3
2. 1
3. 7
4. 0

Answer. 4. 0

Question 23. Identify true statement from the following

1. -7 is to the left of 0
2. -3 is to the right of 1
3. -7 – 3 = -6
4. -1, -2, -3, -4 ….. are positive integers.

Answer. 1. -7 is to the left of 0

Question 24. The fish is 20 meters below the water surface can be denoted as

1. 21 m
2. -10 m
3. -20 m
4. 20 m

Answer. 3. -20 m

Question 25. Number of integers between 2017 and 2018 is

1. 0
2. 1
3. 3
4. does not exist

Answer. 1. 0

Question 26. -6 – 13 + 19 = …….

1. 10
2. -11
3. 0
4. 8

Answer. 3. 0

Question 27. ….. + (-16) = 20

1. 36
2. 20
3. 10
4. 12

Answer. 1. 36

Question 28. The profit of Rs 200/- is represented as

1. +200
2. -200
3. Both A & B
4. None

Answer. 1. +200

Question 29. 4° C below 0° is represented as

1. +4° C
2. -4° C
3. Both A & B
4. None

Answer. 2. -4° C

Question 30. Positive integers are

1. Whole numbers
2. Natural numbers
3. Both A & B
4. None

Answer. 2. Natural numbers

Question 31. Non negative integers are

1. Natural numbers
2. Either natural numbers or whole numbers
3. Whole numbers
4. Both B & C

Answer. 2. Either natural numbers or whole numbers

Question 32. Number of integers between -5 and 5

1. 10
2. 8
3. 9
4. 11

Answer. 3. 9

Question 33. Identify the false statement from the following

1. Zero is the right side of -3
2. Every positive integer is greater than zero
3. There are infinite integers in the number system
4. All integers are whole numbers

Answer. 4. All integers are whole numbers.

Question 34. The sum of two positive numbers is always

1. Positive
2. Negative
3. Either positive nor negative
4. Neither positive nor negative

Answer. 1. Positive

Question 35. The sum of two negative numbers is always

1. Positive
2. Negative
3. Either positive or negative
4. Neither positive nor negative

Answer. 1. Positive

Question 36. The sum of a positive and a negative number is

1. Positive
2. Negative
3. Either positive or negative
4. All above

Answer. 2. Negative

Question 37. a – (-a) =

1. a
2. 2a
3. 0
4. \(a^2\)

Answer. 2. 2a

Question 38. The biggest among -6, 0, 7, 1, -7, -9 is

1. -9
2. -7
3. 7
4. 0

Answer. 3. 7

Question 39. Add (-5) + (-5) + (-5) + 0

1. 15
2. -5
3. 0
4. -15

Answer. 4. -15

Question 40. Add the number 5 to additive inverse of -8 is

1. 11
2. -1
3. 1
4. 0

Answer. 2. -1

Question 41. Subtract 7 from additive inverse of -8 is

1. -1
2. 15
3. 1
4. -15

Answer. 3. 1

Question 42. Add additive inverse of 6 and additive inverse of -5

1. 1
2. -1
3. 11
4. -11

Answer. 2. -1

Question 43. Simplify 30 + (-30) + (-70) + 70 + 0

1. 100
2. 200
3. 0
4. 10

Answer. 3. 200

Question 44. Successor of -7 is ………

1. -4
2. -9
3. -2
4. -6

Answer. 4. -6

Question 45. Predecessor of 12 is ……

1. 1
2. 11
3. 13
4. 10

Answer. 2. 11

Question 46. Five numbers less than ‘0’ is ……

1. -1
2. -3
3. -4
4. -5

Answer. 4. -5

Question 47. The opposite of 2 km south is ………

1. 2 km south
2. 2 km east
3. 2 km north
4. none

Answer. 3. 2 km east

Question 48. 12 + ……… = 12

1. 0
2. 1
3. 4
4. 3

Answer. 1. 0

Question 49. (-4) + (+3) = …….

1. 7
2. 3
3. -1
4. 1

Answer. 3. -1

Question 50. -11 + (-12) = ……

1. -23
2. 23
3. 4
4. 1

Answer. 1. -23

Question 51. (-1) + (0) = ……

1. 4
2. 1
3. 0
4. -1

Answer. 4. -1

Question 52. (-9) + (+4) + (-6) + (+3) = ………

1. 6
2. -8
3. -7
4. 0

Answer. 2. -8

Question 53. -8 – (-10) = ……….

1. 2
2. -2
3. 10
4. 8

Answer. 1. 2

Haryana Board Class 6 Maths Solutions For  Chapter 6 Integers Fill in the blanks:

Question 54. 3 – 4 – 10 = ……….

Answer. -17

Question 55. a + (-a) ……….

Answer. 0

Question 56. 6 + (-10) + 5 + 17 = ………..

Answer. +6

Question 57. -16 – (-23)…. -6 + (-12) (Use >, < or =)

Answer. >

Question 58. …….. + (-51) = 100

Answer. 151

Question 59. Number of integers lying between-3 and 3 is ………

Answer. 5

Question 60. By arranging the following numbers in descending order, the middle integer is 7,8,0,-6,-5,-4,3 …………

Answer. 0

Question 61. Subtract-10 from – 10, we get ……….

Answer. 0

Question 62. Additive inverse of 17 is ……

Answer. +17

Question 63. ………. is neither positive nor negative integer.

Answer. 0

Question 64. (-4) + 6 …….(7-1) (use > or <)

Answer. <

Question 65. 35 – (20) …………

Answer. 15

Question 66. 12 + (-7) = …………….

Answer. 5

Question 67. (-6) + (-2) = ……….

Answer. -8

Question 68. 5 + (12) + 0 = ……….

Answer. 17

Question 69. ……………… is the successor of 7.

Answer. 8

Question 70. The predecessor of -2 is ………

Answer. -3

Question 71. 0. ………. 8 (use < or >)

Answer. <

Question 72. The collection of numbers 1, 2, 3, 4, …. are called …… numbers.

Answer. natural

Question 73. The sum of 137 and -137 is …………..

Answer. 0

Question 74. (-7) + (-3) + (+3) + (+7) = ……….

Answer. 0

Question 75. The loss of 200 in a business is represented as ……..

Answer. -200

Question 76. At a particular place morning temperature is 30°C. It has increased by 6°C by lunch time. At lunch time the temperature. ……………

Answer. 36°C

Question 77. The temperature recorded in Jammu at 6 o’ clock was 7°C. Every one hour the tempera- ture decreases by 2°C. At 10 o’ clock the temperature is …..

Answer. -1°C

Question 78. 5 + (-2) + (-1)= …….

Answer. 2

Question 79. The nearest positive integer to zero is ……..

Answer. +1

Question 80. Which is greater (-2) or (-1) ……….

Answer. -1

Question 81. Which is smaller 3 and -5 ………

Answer. -5

Question 82. The additive inverse of (-9) is ………

Answer. 9

Question 83. The depth below the sea level is denoted by ……. numbers.

Answer. negative

Question 84. Write the number between the least positive integer and the greatest negative integer is ……..

Answer. 0

Question 85. Use > or < in the box (-4) ……… (-10)

Answer. >

86. The subtraction of integers is the same as the addition of their ………

Answer. additive inverse

Haryana Board Class 6 Maths Solutions For  Chapter 6 Integers Match the following:

Question 87.

Answer. 1-E, 2-D, 3-A, 4-B, 5-C

Haryana Board Class 6 Maths Solutions For  Chapter 11 Algebra

• The branch of mathematics in which we study numbers is arithmetic.
• The branch of mathematics in which we study shapes is geometry.
• ‘n’ is an example of a variable. Its value is not fixed. It can take any value 1,2,3,4…
• The main feature of algebra is the use of letters or alphabet to represent numbers.
• We can make different patterns and shapes using match sticks. The relation between the patterns and number of sticks used is observed to frame rules.
• Number of matchsticks required = 3x No. of triangles to be formed.
• We may use any letter (small case alphabet) a, b, m, n, p, q, x, y, z etc…… to represent a variable.
• An expression is made up of variables and constants using different operations.
  Eg: 2x, 3m – 1, 3s + 7, 8p, \(\frac{y}{3}\) etc..
• Variables allow us to express many common rules of geometry and arithmetic in a more general way.
• A mathematical statement consisting of an equal symbol between two algebraic expressions that have the same value is called ‘Algebraic Equation’.
  Eg: 3m = 12, 2x + 1 = 10, 3p + 5 = 2p + 6….. etc.,
• Algebra is a powerful tool for solving ‘puzzles’, ‘riddles’ and problems in our daily life.

Haryana Board Class 6 Maths Solutions For  Chapter 11 Algebra Exercise 11.1

Question 1. Find the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.

a) A pattern of letter T as T

b) A pattern of letter Z as Z

c) A pattern of letter U as U

d) A pattern of letter V as V

e) A pattern of letter E as E

f) A pattern of letter S as S

g) A pattern of letter A as A

Solution. a) Number of matchsticks required = 2n

b) Number of matchsticks required = 3n

c) Number of matchsticks required =3n

d) Number of matchsticks required = 2n

e) Number of matchsticks required = 5n

f) Number of matchsticks required = 5n

g) Number of matchsticks required = 6n

Haryana Board Class 6 Maths Algebra Solutions

Question 2. We already know the rules for the pat- tern of letters L, C and F. Some of the letters from Q. 1 (given above) give us the same rule as that given by L. Which are these? Why does this happen?

Solution. The letters T and V that has pattern 2n, since 2 match sticks are used in all these letters.

Question 3. Cadets are marching in a parade. There are 5 cadets in a row. What is the rule which gives the number of cadets, given the number of rows? (Use ‘n’ for the number of rows.)

Solution. Number of cadets = 5n

Question 4. If there are 50 mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? (Use ‘b’ for number of boxes.)

Solution. Total number of mangoes = 50 b.

Question 5. The teacher distributes 5 pencils per student. Can you tell how many pencils are needed, given the number of students? (Use’s ‘for the number of students.)

Solution. Number of pencils needed = 5 s.

Question 6. A bird flies 1 kilometer in one minute. Can you express the distance covered by the bird in terms of its flying time in minutes. (Use t’ for flying time in minutes)

Solution. Distance covered by the bird in t minutes = t kilometres.

Question 7. Radha is drawing a dot Rangoli (a beautiful pattern of lines joining dots with chalk powder. She has 9 dots in a row. How many dots will her Rangoli have for r rows? How many dots are there if there are 8 rows? If there are 10 rows?

Solution. Number of dots her Rangoli will have for ‘r’ rows = 9r.

Number of dots if there are 8 rows = 8 x 9 = 72.

Number of dots if there are 10 rows = 10 × 9 = 90.

Class 6 HBSE Maths Chapter 11 Algebra Important Questions

Question 8. Leela is Radha’s younger sister. Leela is 4 years younger than Radha. Can you write Leela’s age in terms of Radha’s age? Take Radha’s age to be x years.

Solution. Radha’s age = x years.

Leela’s age = (x – 4) years

Question 9. Mother has made laddus. She gives some laddus to guests and family members; still 5 laddus remain. If the number of laddus mother gave away is 1, how many laddus did she make?

Solution. Number of laddus she made l + 5.

Question 10. Oranges are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still 10 oranges remain outside. If the number of oranges in a small box are taken to be x, what is the number of oranges in the larger box?

Solution. Number of oranges in the larger box = 2x + 10.

Question 11. a) Look at the following matchstick pattern of squares. The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares.

(Hint: If you remove the vertical stick at the and you will get a pattern of CS)

b) Gives a matchstick pattern of triangles. As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.

Solution. a) Number of matchsticks = 3n + 1, n= number of squares.

b) Number of matchsticks = 2n + 1, n = number of triangles.

Haryana Board Class 6 Maths Solutions For  Chapter 11 Algebra Very Short Answer Questions

Question 1. Make a rule between the number of blades required and the number of fans (say n) in a hall?

Solution. A rule between the number of blades required and number of fans (say n) in a hall is 3n.

Question 2. Harshini says that she has 5 biscuits more than Padma has. How can you express the relationship using the variable ‘y’?

Solution. Let the number of biscuits that Padma has = ‘y’.

Harshini says that she has 5 biscuits morethan Padma has.

∴ Number of biscuits that Harshini has = y + 5

Solving Simple Equations Class 6 Haryana Board

Question 3. Prabhakar has ‘p’ number of balls. Number of balls with Devi is 3 times the balls with Prabhakar. Write this as an expression.

Solution. Number of balls that Prabhakar has = p Devi has 3 times of the balls with Prabhakar

∴ The required expression is = 3 x p = 3p

Question 4. Find the general rule for the perimeter of a rectangle. Use variables ‘l’ and ‘b’ for length and breadth of the rectangle respectively.

Solution. Length of the rectangle = 1 units

Breadth = b units

Perimeter = 1 + b + 1 + b

= 21 + 2b

= 2(1 + b) units

Question 5. Find the general rule for the area of a square by using the variable ‘s’ for the side of a square.

Solution. Side of a square = s units

Area of a square = side x side = s x s

= s2 square units

Algebraic Expressions Class 6 HBSE Notes

Haryana Board Class 6 Maths Solutions For  Chapter 11 Algebra Short Answer Questions

Question 1. Arrange 2 matchsticks to form the shape

Continue the same shape for 2 times, 3 times and 4 times. Frame the rule for repeating the pattern.

Solution.

Number of matchsticks required for shape – 1 is 2 = 2 × 1 = 2 × 1 times

Number of matchsticks required for shape – 2 is 4 = 2 x 2 = 2 × 2 times

Number of matchsticks required for shape – 3 is 6= 2 × 3 = 2 × 3 times

Number of matchsticks required for shape – 4 is 8.2 x 4 = 2 × 4 times

∴ The rule for number of matchsticks required for n times for the shape is = [2 x n] times.

Question 2. A line of shapes is constructed using matchsticks.

Basic Algebra Problems For Class 6 With Solutions

1) Find the rule that shows how many sticks are needed to make a line of such shapes.

Solution.

∴ Number of matchsticks = 2 x (Number of shapes) + 1

Let s = Number of shapes

m = Number of matchsticks

∴ Number of matchsticks = m = 2s + 1

2) How many matchsticks are needed to form shape 12 ?

Solution. Number of matchsticks needed to form shape 12

= 2 × 12 + 1

= 24 + 1 = 25

Question 3. Find the rule which gives the number of matchsticks required to make the following matchstick patterns.

1) A pattern of letter ‘T’

2) A pattern of letter ‘E’

3) A pattern of letter ‘Z’

Solution. 1)

Number of matchsticks required to make a pattern of letter ‘T’ is 3

∴ The rule is 3 m.

2)

Number of matchsticks required to make a

pattern of letter ‘E’ is 4

∴ The rule is 4m

Word Problems On Algebra For Class 6 Haryana Board

3)

Number of matchsticks required to make a

pattern of letter ‘Z’ is 3

∴ The rule is 3m

Question 4. Find a rule for the following pattern between number of shapes formed and number of matchsticks required.

Solution. a) Number of match sticks used for this pattern is 2, 4, 6, ……… Rule is – 2n

b) Number of match sticks used for this pattern is 3, 6, 9, …… Rule is – 3n

Question 5. 1) How many match sticks are required to form a triangle?

Solution. To make a triangle 3 match sticks are required.

2) Complete the following table: Write the rule.

Solution. The rule is “number of matchsticks required = 3 times the number of triangles to be formed.”

Question 6. 1) How many matchsticks are required to form a square?

Solution. To make a square 4 matchsticks are required..

2) Complete the following table: Write the rule.

Solution. The rule is “Number of matchsticks required = 4 times number of squares to be formed”.

Haryana Board Class 6 Maths Solutions For  Chapter 11 Algebra Long Answer Questions

Question 1. Rita took matchsticks to form the shape

She repeated the pattern and gave a rule

Number of matchsticks needed = 6.y, where y is the number of shapes to be formed.

Is it correct? Explain.

What is the number of sticks needed to form 5 such shapes?

Solution.

Number of match sticks required for shape – 1 is 6 = 6 × 1 times

Number of match sticks required for shape – 2 is 12 = 6 x 2 times

Number of match sticks required for shape – 3 is 18 = 6 x 3 times

Number of match sticks required for shape – 4 is 24 = 6 × 4 times

Number of match sticks required for shape 5 is 30 = 6 x 5 times

∴ Number of match sticks needed for the shape y is = 6 x y

[Where y is the number of shapes to be formed]

Yes, Rita is correct.

Number of match sticks needed to form 5 shapes = 6 x 5 = 30

Question 2. Find the nth term in the following sequences

(1),3,6,9,12,…

(2) 2,5,8,11,…

(3) 1, 4, 9, 16,…

Solution. 1) 3,6,9,12.

3 = 3 × 1

6 = 3 × 2

9 = 3 × 3

12 = 3 × 4

n^th term of the sequence = 3 x n

[∴ n is a natural number]

2) 2,5,8,11

2 = 3 x 1 – 1

5 = 3 × 2 – 1

8 = 3 × 3 – 1

11 = 3 x 4 – 1

n^th term of the sequence = 3 x n – 1

[∴ n is a natural number]

3) 1, 4, 9, 16……………….

1 = \(\mathrm{1}^2\)

4 = \(\mathrm{2}^2\)

9 = \(\mathrm{3}^2\)

16 = \(\mathrm{4}^2\)

n^th term of the sequence = \(\mathrm{n}^2\)

[∴ n is a natural number]

Haryana Board Class 6 Maths Solutions For  Chapter 11 Objective Type Questions

Choose the correct answer :

Question 1. The symbol used in equation is

1. >
2. =
3. <
4. ≠

Answer. 2. =

Question 2. How many sticks are needed to prepare the letter Z?

1. 6
2. 7
3. 2
4. 3

Answer. 4. 3

Question 3. 2, 4, 6, ……… nth term is …………

1. \(\frac{n}{2}\)
2. 2n
3. 4n
4. \(\mathrm{n}^2\)

Answer. 2. 2n

Class 6 Maths Variables And Constants Explained

Question 4. Statement – A: An expression is made up of variables and constants using different operations.

Statement – B: A mathematical statement consisting of an equal symbol between two algebraic expressions is called ‘Algebraic equation’

1. Both A & B are true
2. A is true, B is false
3. A is false, B is true
4. Both A & B are false

Answer. 1. Both A & B are true

Question 5. Write the statement for the expression 3m + 11

1. 11 more than three times of m
2. 11 is added to thrice the m
3. 11 times more than thrice them
4. Both A & B

Answer. 4. Both A & B

Question 6. Statement – A: Solution of an equation is the value of the variable for which LHS and RHS are equal.

Statement – B: The solution is also called root of the equation.

1. Both A & B are true
2. A is true, B is false
3. A is false, B is true
4. Both A & B are false

Answer. 1. Both A & B are true

Question 7. 3, 6, 9, 12 ………. nth term is

1. 2n
2. n + 3
3. 3n
4. \(\frac{n}{3}\)

Answer. 3. 3n

Question 8. The nth term of 2, 5, 8, 11 …….

1. 3n
2. 3n – 1
3. 3n + 1
4. 2n + 1

Answer. 2. 3n – 1

Question 9. The nth term of 1, 4, 9, 16 ……..

1. \(\mathrm{n}^2\)
2. 2n
3. 2n – 1
4. n + 2

Answer. 1. \(\mathrm{n}^2\)

Haryana Board Class 6 Maths Solutions For  Chapter 11 Algebra Fill in the blanks:

Question 10. 1, 4, 9, 16. nth term is ……..

Answer. \(\mathrm{n}^2\)

Question 11. The cost of one book is 101 then the cost of p such books is ………

Answer. ₹ 101p

Haryana Board Class 6 Maths Solutions For  Chapter 4 Basic Geometrical Ideas

• The term ‘GEOMETRY’ is derived from the Greek word ‘GEOMETRON’.
• ‘Geo’ means earth and ‘metron’ means ‘measurement’.
• ‘Euclid’ is known as ‘Father of Geometry’. He introduced geometry in a logical order in the book ‘The Elements’..
• The ancient Indian Mathematician Aryabhata and Brahmagupta contributed their works in geometry.
• A ‘point’ determines a location. It is usually denoted by capital letters in English.
• A ‘line segment’ is formed by joining two points. It has a fixed length. A line segment has negligible thickness. It has two end points.

• A ‘line’ is obtained when a line segment extends on both sides indefinitely. It is denoted by small letters such as l, m, n etc.

• It has no end points.
• A’ray’ is a portion of a line starting at a point and goes in one direction endlessly.

• Eg: Ray \(\overrightarrow{\mathrm{AB}}\) Ray \(\overrightarrow{\mathrm{CA}}\)
• By using divider and scale, we can measure the length of line segment.
• A figure drawn without lifting a pencil is called a ‘curve’. In this sense, a line is also a curve.
• Parallel Lines: The lines in a plane that never meet even if they are extended any further are called Parallel lines. Eg: The lines in your ruled book are parallel lines.

• If line l is parallel to line ‘m’, then it is denoted by l || m. It can be read as “l is Parallel to m”.
• Intersecting Lines: The lines that cross one another are called intersecting lines and the point at which they intersect is called intersecting point.

Haryana Board Class 6 Maths Basic Geometrical Ideas solutions

• Here ‘O’ is the intersecting point.
• Concurrent Lines: Three or more lines passing through the same point are called concurrent lines. The point is called point of concurrency.

• Perpendicular Lines: The angle between any two lines is 90° are called ‘perpendicular lines’: It is denoted by ⊥ (perpendicular).
• If line l is perpendicular to the line m then it is denoted by l ⊥ m and read as ‘I is perpendicular to m’.

• Angle: An angle in a figure formed by two rays with a common end point. The common end point is called ‘vertex’. The rays are the ‘sides or arms’ of the angle. It is denoted by ‘∠AOB’ read as angle АОВ.

Types of angles.

• We use a tool called “Protractor” to measure the given angle.
• Two rays with a common initial make two regions.
• The interior of an angle is the group of all the points between the rays of the angle.
• The exterior of an angle is the group of all points outside the rays of the angle.

• The simple closed figure formed by three line segments is called a triangle.
• The line segments are called sides.
• A triangle has three vertices, three sides and three angles.
• In triangle ABC

A, B, C are three vertices \(\overline{A B}, \overline{B C}, \overline{C A}\) are three sides ∠BAC, ∠ABC, ∠ACB are three angles. The triangle ABC is denoted by ΔABC.

• A triangle divides a plane into three parts
  1. Interior of the triangle
  2. Boundary of the triangle
  3. Exterior of the triangle

Eg. PQR is a triangle.

The points 0, B, S are interior of the tri- angle.

The points A, C are on the Boundary of the trianlge.

The points T, U, V are exterior of the tri- angle.

• A ‘simple curve’ is one that does not cross itself.
• Curves are of 2 types – open curve; closed curve

• A figure is a ‘polygon’ if it is a simple closed figure made up definite number of line segments
• A closed figure separates the plane into three parts.
  1. Interior (inside) of the figure.
  2. Boundary of the figure.
  3. Exterior (outside) of the figure.
• The interior of the figure together with its boundary is its ‘region’.

Eg. : ABCD is a closed figure formed by 4 line segments AB, BC, CD and DA.

Points P, Q are Interior of the figure, points R, S are on the Boundary line, points T, U are on the exterior of the figure.

• The interior of the figure together with its boundary is its region

Question 1. A Star in the sky also gives us an idea of a point. Identify at least five such situations in your daily life.

Solution. Five situations giving an idea of a point are:

1. Sharp tip of pencil.
2. Tip of a pen
3. Tip of the compass
4. Pointed end of the needle
5. Dot on the paper

Question 2. Name the line segments in the figure 4.2. Is A, the end point of each line segment?

Solution.

The line segments in the given figure are

\(\overline{\mathrm{AB}}\) (or \(\overline{\mathrm{BA}}\)) and \(\overline{\mathrm{AC}}\) (or \(\overline{\mathrm{CA}}\))

Yes! A is the end point of each line segment.

Points, lines, and angles Class 6 HBSE Maths

Question 3. 1. Name the rays given in this picture.

2. Is T a starting point of each of these rays?

Solution. 1) \(\overrightarrow{\mathrm{TA}}, \overrightarrow{\mathrm{TN}}, \overrightarrow{\mathrm{~TB}}, \overrightarrow{\mathrm{NB}}\)

2) No! T is not a starting point of each of these rays.

Haryana Board Class 6 Maths Solutions For  Chapter 4 Basic Geometrical Ideas Exercise 4.1

Question 1. Use the figure to name :

a) Five points

b) A line

c) Four rays

d) Five line segments

Solution. a) O, B, C, D, E

b) DB

c) \(\overrightarrow{O B}, \overrightarrow{O C}, \overrightarrow{O E}, \overrightarrow{O D}\)

d) \(\overline{O B}, \overline{O C}, \overline{O E}, \overline{O D}, \overline{E D}\)

Question 2. Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given.

Solution. Let the four points be A, B, C and D.

AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB, DC.

Question 3. Use the figure to name:

a) Line containing point E.

b) Line passing through A.

c) Line on which O lies.

d) Two pairs of intersecting lines.

Solution.

a) EF

b) AE

c) OC

d) AE and CO; AE and EF.

Question 4. How many lines can pass through

a) one given point?

b) two given points?

Solution. a) Infinitely many lines can pass through one given point.

b) One and only one line can pass through two given points.

Question 5. Draw a rough figure and label suitably in each of the following cases:

a) Point Plies on \(\overleftrightarrow{\mathrm{AB}}\)

b) \(\overleftrightarrow{\mathrm{XY}}\) and \(\overleftrightarrow{\mathrm{PQ}}\) intersect at M.

c) Line I contains É and F but not D.

d) \(\overleftrightarrow{\mathrm{OP}}\) and \(\overleftrightarrow{\mathrm{OQ}}\) meet at O.

Solution.

Question 6. Consider the following figure of line \(\overline{\mathbf{M N}}\). Say whether following statements are true or false in context of the given figure.

a. Q, M, O, N, P are points on the line \(\overline{\mathbf{M N}}\)

Solution. True.

b. M, O, N are points on a line segment \(\overline{\mathbf{M N}}\)

Solution. True

c. M and N are end points of line segment \(\overline{\mathbf{M N}}\)

Solution. True

d. O and N are end points of line segment \(\overrightarrow{\mathrm{OP}}\)

Solution. False.

e. M is one of the end points of the line segment \(\overline{\mathbf{Q O}}\)

Solution. False.

f. M is point on ray \(\overrightarrow{\mathrm{OP}}\).

Solution. False.

g. Ray \(\overrightarrow{\mathrm{OP}}\) is different from ray \(\overrightarrow{\mathrm{QP}}\).

Solution. True.

h. Ray \(\overrightarrow{\mathrm{OP}}\) is same as ray \(\overrightarrow{\mathrm{OM}}\).

Solution. False.

i. Ray \(\overrightarrow{\mathrm{OM}}\) is not opposite to ray \(\overrightarrow{\mathrm{OP}}\).

Solution. False.

j. ‘O’ is not an initial point of ray \(\overrightarrow{\mathrm{OP}}\).

Solution. False.

k. N is the initial point of \(\overrightarrow{\mathrm{NP}} \text { and } \overrightarrow{\mathrm{NM}}\).

Solution. True

Haryana Board Class 6 Maths Solutions For  Chapter 4 Basic Geometrical Ideas Exercise – 4.2

Question 1. Classify the following curves as

(1) Open or

(2) Closed.

Solution. (1) a, c – open curves

(2) b, d, e – closed curves.

Question 2. Draw rough diagrams to illustrate the following:

(a) Open curve

(b) Closed curve

Solution.

Types of angles in geometry Class 6 Haryana Board

Question 3. Draw any polygon and shade its interior.

Solution.

Question 4. Consider the given figure and answer the questions:

a) Is it a curve?

b) Is it closed?

Solution. a) Yes! it is a curve.

b) Yes! it is closed.

Question 5. Illustrate, if possible, each one of the following with a rough diagram:

Solution. a) A closed curve that is not a polygon.

b) An open curve made up entirely of line segments.

c) A polygon with two sides.

Not Possible.

A: A polygon is a closed plane figure with three or more sides that are all straight. Therefore, A polygon with two side cannot be drawn.

Haryana Board Class 6 Maths Solutions For  Chapter 4 Basic Geometrical Ideas Exercise – 4.3

Question 1. Name the angles in the given figure.

Solution. ∠ABC, ∠BCD, ∠CDA, ∠DAB

Question 2. In the given diagram, name the point(s)

a) In the interior of DOE

b) In the exterior of ZEOF

c) On ∠EOF

Answer. a) A

b) C, A, D

c) O, B, E, F

Polygons and their properties Class 6 HBSE Maths

Question 3. Draw rough diagrams of two angles such that they have

a. One point in common

Solution.

∠AOB and ∠BOC have one point ‘O’ in common.

b. Two points in common.

Solution. ∠AOB and ∠OBC have two points O and B in common.

c. Three points in common.

Solution. Not possible

d. Four points in common.

Solution. Not possible

e. One ray in common.

Solution. ∠AOB and ∠BOC have one ray OB in common.

Chapter 4 Basic Geometrical Ideas Very Short Answer Questions

Question 1. Draw a line, ray and a line segment.

Solution.

Question 2. Mark two points X and Y. Also mark three more points between them and another three points that are not in between those two points.

Solution. X, Y are any two points.

P, Q, R are three points between X and Y.

A, B, C are three points not between X and Y.

Question 3. Define a triangle. Write the parts in it.

Solution. A simple colsed figure formed by three line segments is called a triangle. It has 3 sides, 3 vertices and 3 angles.

Question 4. Join the points given below. Name the line segments so formed in the figure.

Solution. 1)

Line segments so formed are: \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CA}}\)

2)

Line segments so formed are: \(\overline{\mathrm{PQ}}, \overline{\mathrm{QR}}, \overline{\mathrm{RS}}, \overline{\mathrm{ST}}, \overline{\mathrm{TP}}\)

Parts of a circle Class 6 HBSE Maths

Question 5. Which of the following has a definite length?

1) Line

2) Point

3) Line segment

4) Ray

Solution. Line segment. Because it has two end points.We can measure it.

Question 6. Tell which letter is an example of simple curve.

Solution. The letter O is an example of simple curve.

Question 7. What is the least no. of sticks needed to form a closed figure?

Solution. Three sticks are needed to form a closed figure.

Haryana Board Class 6 Maths Solutions For  Chapter 4 Basic Geometrical Ideas Short Answer Questions

Question 1. From the adjacent figure, write down

1) The sides of the triangle

2) The angles of the triangle

3) The vertices of the triangle.

Solution. 1) The sides of the triangle – \(\overline{\mathrm{MN}}, \overline{\mathrm{NH}}, \overline{\mathrm{HM}}\)

2) The angles of the triangle – ∠HMN, ∠MNH, ∠NHM

3) The vertices of the triangle – H, M, N

Question 2. Write the set of parallel lines and perpendicular lines in the given figure by using symbols.

Solution. Parallel lines: \(\overline{\mathrm{AB}} \text { and } \overline{\mathrm{DC}} ; \overline{\mathrm{AB}} \| \overline{\mathrm{DC}} ; \overline{\mathrm{AQ}} \text { and } \overline{\mathrm{PC}} ; \overline{\mathrm{AQ}} \| \overline{\mathrm{PC}}\)

Perpendicular lines: \(\overline{\mathrm{AD}} \perp \mathrm{AB} \text { and } \overline{\mathrm{AD}} \perp \mathrm{DC}\)

Question 3. Draw

1) Intersecting lines

2) Parallel lines

3) Perpendicular lines.

Solution.

1) Intersecting lines

2) Parallel lines

3) Perpendicular lines

Question 4. Name the following from the figure.

1) Any five points : A, B, C, D, O

2) Any five line segments : \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CD}}, \overline{\mathrm{DA}}\)

3) Any three rays : \(\overrightarrow{\mathrm{OA}}, \overrightarrow{\mathrm{OB}}, \overrightarrow{\mathrm{OC}}\)

4) Any two lines : \(\overrightarrow{\mathrm{AC}}, \overrightarrow{\mathrm{BD}}\)

Question 5. Move your pencil along the following english letters and state which are open and which are closed.

Solution. (i), (iii), (iv) are open, (ii) is closed.

Question 6. Tick the figures which are simple curves.

Solution. Simple curves: (i), (ii), (iv)

Question 7. State which curves are open and which are closed.

Solution. Open curves: (i), (v)

Closed curves: (ii), (iii), (iv)

Question 8. Mark the points in the figure which satisfy all the three conditions.

1) A, B in the interior of ∠DOF

2) A, C in the exterior of ∠EOF

3) B is on ∠DOE

Solution.

Question 9. Identify simple closed and open figures from the figures given here under.

Solution. Simple closed figures – a, c, d;

Simple open figure – b

Question 10. Identify simple curved figures.

Solution. (ii), (iii), (vi) are simple curved figures.

Haryana Board Class 6 Maths Solutions For  Chapter 4 Basic Geometrical Ideas Long Answer Questions

Question 1. Write the names of the angles, their vertices and arms.

Solution.

Question 2. From the adjacent figure write the points that belongs to

1) the angle

2) the interior of the angle

3) the exterior of the angle

Solution. The points that belongs to

1) The angle – B, R, E, O, C, A

2) The interior of the angle – D, F, Q

3) The exterior of the angle – M,L, N

Question 3. From the adjacent figure write

1) Interior points of the triangle.

2) Exterior points of the triangle.

3) Points on the boundary of the triangle.

4) Vertices of the triangle.

Solution. 1) Interior points of the triangle – B, M

2) Exterior points of the triangle – A, C, N

3) Points on the boundary of the triangle – P, Q, R, D, L

4) Vertices of the triangle-P, Q, R

Question 4. Write ‘True’ or ‘False”.

1) A line has no end points.

True

2) Ray is a part of a line.

True

3) A line segment has no definite length.

False

4) A line segment has only one end point.

False

5) We can draw many lines through a point.

True

Question 5. Identify which are simple curves and which are not?

Solution. If a curve does not cross itself then it is a simple curve.

(i), (ii), (iv) are simple curves.

(iii) The curve crosses it self so it is not a simple curve.

Question 6. Name the points that lie in the interior, on boundary and in the exterior of the figure.

Solution. The points that lie

1) Interior – A, B, E, G, I;

2) Boundary – K, F, C;

3) Exterior – J, D

Question 7. Draw three simple closed figures:

1) By straight lines only.

Solution.

2) By straight lines and curved lines both.

Solution.

Question 8. Name the angles, vertex and arms of the angles from the figure.

Difference between line and line segment Class 6

Question 9. In the figure given below, Identify which points lie

1) in the interior,

2) in the exterior,

3) on the boundary.

Solution. 1) Interior points – A, T, Q, I

2) Exterior points – B, D, L, K

3) On the boundary-C, E

Question 10. Observe the adjacent figure. Write answers for the following.

Solution. 1) Name : PQRS Quadrilateral

2) Vertices : P, Q, R, S

3) Sides : \(\overline{\mathrm{PQ}}, \overline{\mathrm{QR}}, \overline{\mathrm{RS}}, \overline{\mathrm{SP}}\)

4) Angles : ∠SPQ, ∠PQR, ∠QRS, ∠RSP

5) Opposite sides : \(\overline{\mathrm{PQ}}, \overline{\mathrm{RS}} ; \overline{\mathrm{QR}}, \overline{\mathrm{PS}}\)

6)Opposite angles : ∠SPQ, ∠QRS; ∠PQR, ∠RSP

7) Adjacent angles : ∠SPQ, ∠PQR, ∠QRS, ∠RSP, ∠SPQ

Haryana Board Class 6 Maths Solutions For  Chapter 4 Basic Geometrical Ideas Objective Type Questions

Choose the correct answer:

Question 1. How many end points does a line have?

1. Infinite
2. 2
3. 0
4. 1

Answer. 4. 1

Question 2. How many end points does a line have?

1. No end points
2. 2
3. Infinite
4. 1

Answer. 1. No end points

Question 3. The closed figure formed by more line segments is called

1. square
2. polygon
3. triangle
4. circle

Answer. 2. polygon

Question 4. We denote line AB as

1. \(\overrightarrow{\mathrm{AB}}\)
2. \(\overline{\mathrm{AB}}\)
3. \(\overleftrightarrow{\mathrm{AB}}\)
4. \(\widehat{\mathrm{AB}}\)

Answer. 3. \(\overleftrightarrow{\mathrm{AB}}\)

Question 5. Number of points on a line

1. 3
2. 2
3. 4
4. Infinite

Answer. 4. Infinite

Question 6. There are …… vertices in a triangle.

1. 4
2. 3
3. 2
4. 8

Answer. 2. 3

Question 7. In the figure vertex of the angle is …..

1. P
2. O
3. R
4. \(\overrightarrow{\mathrm{OP}}\)

Answer. 2. O

Observe the following figure and answer the following questions from 8 to 10.

Word problems on basic geometrical ideas for Class 6 HBSE

Question 8. Interior point

1. X
2. L
3. P
4. Z

Answer. 3. P

Question 9. Exterior points

1. X,L
2. Z,L
3. O,P
4. X,Z

Answer. 2. Z,L

Question 10. Points on the ray \(\overrightarrow{\mathrm{OB}}\)

1. X
2. Z
3. P
4. O

Answer. 1. X

Question 11. Number of vertices of a square is ……..

1. 3
2. 4
3. 8
4. 13

Answer. 2. 4

Question 12. Triangle PQR can be denoted by …….

1. PΔQR
2. ΔPQR
3. QRPΔ
4. PQR

Answer. 2. ΔPQR

Question 13. How many lines can be drawn through a point in a plane?

1. 16
2. 12
3. 3
4. Infinite

Answer. 4. Infinite

Question 14. The symbol of perpendicular is

1. |
2. X
3. ⊥
4. T

Answer. 3. ⊥

Question 15. The symbol of parallel is

1. X
2. ∥
3. ⊥
4. T

Answer. 2. ∥

Question 16. Which of the following are intersecting lines?

1. ∥
2. X
3. *
4. ⊥

Answer. 2. X

Question 17. Two adjacent edges of blackboard are example for …… lines.

1. parallel
2. concurrent
3. perpendicular
4. all above

Answer. 3. perpendicular

Question 18. Two opposite edges of a paper is example for …….. lines.

1. intersecting
2. perpendicular
3. parallel
4. concurrent

Answer. 3. parallel

Question 19. To measure the angle we use

1. divider
2. ruler
3. setsquare
4. protractor

Answer. 4. protractor

Question 20. How many right angles can make a complete angle?

1. 1
2. 2
3. 3
4. 4

Answer. 4. 4

Question 21. End points of a line segment are

1. 0
2. 1
3. 2
4. Infinite

Answer. 3. 2

Question 22. How many lines can be drawn through two points?

1. 0
2. 1
3. 2
4. Infinite

Answer. 2. 1

Question 23. How many line segments lie in the given line?

1. 4
2. 5
3. 6
4. 7

Answer. 3. 6

Question 24. Father of Geometry

1. Phythagoras
2. Ramanujan
3. Euclid
4. Thales

Answer. 3. Euclid

Question 25. The word Geometry is derived from ……. language.

1. Greek
2. Latin
3. Italian
4. Indian

Answer. 1. Greek

Question 26. If two lines cross one another that lines are called

1. Parallel lines
2. Intersecting lines
3. Concurrent lines
4. Perpendicular lines

Answer. 2. Intersecting lines

Question 27. If three or more lines passing through the same point are …….. lines.

1. parallel
2. intersecting
3. concurrent
4. perpendicular

Answer. 3. concurrent

Question 28. The angle between two lines are 90° then they are …… lines.

1. parallel
2. intersecting
3. concurrent
4. perpendicular

Answer. 4. perpendicular

Question 29. If two lines does not meet at any where are ….. lines.

1. parallel
2. intersecting
3. concurrent
4. perpendicular

Answer. 1. intersecting

Question 30. The lines in your ruled book are example of …… lines.

1. intersecting
2. parallel
3. perpendicular
4. concurrent

Answer. 2. parallel

Question 31. Straight angle =

1. 0°
2. 90°
3. 180°
4. 360°

Answer. 3. 180°

Question 32. Complete angle =

1. 0°
2. 90°
3. 180°
4. 360°

Answer. 4. 360°

Question 33. Reflexive angle =

1. 190°
2. 210°
3. 315°
4. all the above

Answer. 4. 315°

Question 34. Flag pole on the earth is an example for …… lines.

1. perpendicular
2. parallel
3. concurrent
4. intersecting

Answer. 1. perpendicular

Question 35. How many common points that parallel lines have

1. 0
2. 1
3. 2
4. Infinite

Answer. 1. 0

Observe the following figure and answer the questions (36 – 37)

Question 36. Identify the perpendicular lines.

1. l, m, n
2. p, m
3. p, n
4. l, m

Answer. 2. p, m

Question 37. Identify the intersecting lines

1. p, l
2. l, m, n
3. p, n and p, m
4. None

Answer. 3. p, l

Question 38. The closed figure formed by more line segments is called …..

1. square
2. polygon
3. triangle
4. circle

Answer. 2. polygon

Question 39. We denote line AB as

1. \(\overrightarrow{\mathrm{AB}}\)
2. \(\overline{\mathrm{AB}}\)
3. \(\overleftrightarrow{\mathrm{AB}}\)
4. \(\overparen{\mathrm{AB}}\)

Answer. 3. \(\overleftrightarrow{\mathrm{AB}}\)

Question 40. The word ‘Geo means ……

1. Geometry
2. Geogre
3. Earth
4. Metron

Answer. 3. Earth

Question 41. A point determines a ……….

1. location
2. line
3. object
4. none

Answer. 1. location

Question 42. Two points determine a …..

1. circle
2. line
3. triangle
4. sector

Answer. 2. line

Question 43. If two lines l1 and l2 are parallel, then we represent this with …..

1. l1,l2
2. l1 ∥ l2
3. l1/l2
4. l2 ∥ l1

Answer. 2. l1 ∥ l2

Question 44. A …… is a portion of line.

1. circle
2. point
3. triangle
4. ray

Answer. 4. ray

Question 45. The line segments forming a polygon are called its …….

1. vertex
2. circle
3. interior
4. side

Answer. 1. vertex

Question 46. The two rays forming the angle are called ………. of the angle.

1. segment
2. common
3. vertex
4. arms

Answer. 4. arms

Question 47. The three sided polygon is called …..

1. quadrilateral
2. line segment
3. side
4. triangle

Answer. 4. triangle

Haryana Board Class 6 Maths Solutions For  Chapter 4 Basic Geometrical Angles Fill in the blanks:

Question 48. 72° is a measure of ……….. angle

Answer. acute

Question 49. A straight angle measures……….

Answer. 180°

Question 50. Your 6th class mathematics text book corner will be taken as a measure of ………

Answer. 90°

Question 51. Half of complete angle. ……………

Answer. 180°

Question 52. Symbolic form of “The line I is parallel to the line m”……….

Answer. 1 || m

Question 53. The angle shown in the figure represents …… angle

Answer. reflex

Question 54. In the figure x° = …………

Answer. 90°

Question 55. The union of two rays having same initial point is called …………..

Answer. angle

Question 56. Ray is a part of line (T/F)

Answer. True

Question 57. In the figure p || q, r is a transversal then x° = …………

Answer. 70°

Question 58………………………… is one that does not cross itself.

Answer. simple curve

Question 59. ……….is the union of two rays with a common point.

Answer. Angle

Question 60. A triangle with its boundary and its interior is called the ………..

Answer. Triangle region

Question 61. Number of end points of a line segment ……….

Answer. 2

Question 62.

Vertex of this angle ………….

Answer. B

Question 63.

Number of closed figures in the adjoining diagram……

Answer. 3

Question 64. Mathematical form of a line segment PQ is.

Answer. PQ

Question 65. How we denote triangle ABC?..

Answer. ΔΑΒC

Question 66. Parallel lines never

Answer. Intersect

Question 67. If two lines \(\overleftrightarrow{\mathrm{AB}}\) and \(\overleftrightarrow{\mathrm{CD}}\) are parallel, we write.

Answer. AB ||CD

Question 68. In a closed curve there are……………………… disjoint parts.

Answer. 3

Question 69. The interior of a curve together with its boundary is called …..

Answer. region

Question 70. A polygon with least number of sides is ……..

Answer. triangle

Haryana Board Class 6 Maths Solutions For Chapter 2 Whole Numbers

• If we add 1 to a number we get successor of that number.
• The natural numbers along with zero form the collection of whole numbers.
• Whole numbers are closed under addition and also under multiplication is called closure property.
• Division means repeated subtraction.
• Division of whole number by ‘0’ is not defined.
• The addition of two numbers can be done in any order.
• We can multiply two whole numbers in any order.
• Addition and multiplication are commutative for whole numbers.
• ‘0’ is the additive identity of whole numbers.
• ‘1’ is the multiplicative identity for whole numbers.
• The numbers which we use for counting are known as natural numbers. It is denoted by ‘N’.
  Set of natural numbers N = {1, 2, 3, 4, …………..}
• The natural numbers along with the zero are called whole numbers. It is denoted by ‘W’.
  Set of whole numbersW= {0, 1, 2, 3, ……………}
• The number just before any natural number is called the ‘Predecessor’.
• The next number of any natural number is called the ‘Successor’.
• Every natural number has a successor. Every natural number except 1 has a predecessor.
• Every whole number has a successor. Every whole number except zero has a predecessor.
• All natural numbers are whole numbers and all whole numbers except zero are natural numbers.
• Whole numbers can be represented on a number line. Operations of addition, subtraction and multiplication can easily be performed on a number line.
• Addition corresponds to moving to the right on the number line, whereas subtraction corresponds to moving to the left. Multiplication corresponds to making jumps of equal distance from zero.
• “The sum of any two whole numbers is always a whole number”. This property is known as the closure property under addition for whole numbers.
  Eg: If a, b are two whole numbers then their sum ‘a + b’ is also a whole number.
• The product of any two whole numbers is always a whole number. This property is known as the ‘closure property under multi- plication for whole numbers’.
  Eg: If a, b are two whole numbers, their product ‘a x b’ is also a whole number.
• Whole numbers are closed under addition and multiplication. But, whole numbers are not closed under subtraction and division.
• Division by zero is not defined.
• If ‘a’ and ‘b’ are two whole numbers then ‘a + b = b + a’ this property is known as ‘Commutative Property’ under addition of whole numbers.
• If ‘a’ and ‘b’ are two whole numbers then ‘a x b = b x a’ this property is known as ‘Commutative Property’ under multiplication of whole numbers.
• Addition and multiplication are ‘Commutative’ over whole numbers. But whole. numbers are not commutative under subtraction and division.
• If a, b and c are three whole numbers then ‘a x (b + c) = (a x b) + (a x c)’ is known as ‘distributive property of multiplication over addition’.
• Addition and multiplication are ‘Associative’ over whole numbers. But whole numbers not associative under subtraction and division.
• If a, b and c are three whole numbers then ‘ax (b+c) = (a x b) + (ax c)’ is known as ‘distributive property of multiplication over addition’.
• Commutativity, associativity and distributivity of whole numbers are useful in simplifying calculations. We often use them without being aware of them.
• Pattern with numbers are not only interesting but also useful especially for mental calculations. They help us to understand properties of numbers better.

Question 1. Write the predecessor and successor of 19; 1997; 12,000; 49; 1,00,000

Solution.

Question 2. Is there any natural number that has no predecessor ?

Solution. Yes, the natural number 1 has no predecessor.

Question 3. Is there any natural number which has no successor? Is there a last natural number?

Solution. No, there is no natural number which has no successor. No, there is no last natural number..

Question 4. Are all natural numbers also whole numbers ?

Solution. Yes, all natural numbers are also whole numbers.

Question 5. Are all whole numbers also natural numbers ?

Solution. No, because the whole number ‘O’ is not natural number.

Question 6. Which is the greatest whole number?

Solution. There is no greatest whole number.

Haryana Board Class 6 Maths Whole Numbers solutions

Question 7. Find 4 + ; 2 + 6; 3 + 5 and 1 + 6 using the number line.

Solution.

∴ 4 + 5 = 9

∴ 2 + 6 = 8

∴ 3 + 5 = 8

∴ 1 + 6 = 7

Question 8. Find 8 – 3; 6 – 2; 9 – 6 using number line.

Solution. 8 – 3

∴ 8 – 3 = 5

6 – 2

∴ 6 – 2 = 4

9 – 6

∴ 9 – 6 = 3

Properties of whole numbers Class 6 HBSE

Question 9. Find 2 x 6; 3 x 3; 4 x 2 using the number line.

Solution.

∴ 2 x 6 = 12

∴ 3 x 3 = 9

∴ 4 × 2 = 8

Chapter 2 Whole Numbers Exercise – 2.1

Question 1. Write the next three natural numbers af- ter 10999.

Solution. The next three natural numbers after 10999 are 11,000, 11,001 and 11,002.

Question 2. Write the three whole numbers occuring just before 10001.

Solution. The three whole numbers occurring just before 10001 are 10000, 9999 and 9998.

Question 3. Which is the smallest whole number?

Solution. The smallest whole number is 0.

Question 4. How many whole numbers are there between 32 and 53 ?

Solution. There are 20 whole numbers between 32 and 53. They are 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51 and 52.

Question 5. Write the successor of:

(a) 2440701

(b) 100199

(c) 1099999

(d) 2345670

Solution. a) The successor of 2440701 is 2440701 + 1 = 2440702

b) The successor of 100199 is 100199 + 1 = 100200

c) The successor of 1099999 is 1099999 + 1 = 1100000

d) The successor of 2345670 is 2345670 + 1 = 2345671

Whole numbers and their operations Class 6

Question 6. Write the predecessor of:

(a) 94

(b) 10000

(c) 208090

(d) 7654321

Solution. a) The predecessor of 94 is 94 – 1 = 93

b) The predecessor of 10000 is 10000 – 1 = 9999

c) The predecessor of 208090 is 208090 – 1 = 208089

d) The predecessor of 7654321 is 7654321 – 1 = 7654320

Question 7. In each of the following pairs of numbers, state which whole number is on the left of the other number on the number line. Also write them with the appropriate sign (>, <) between them.

(a) 530,503

(b) 370,307

(c) 98765, 56789

(d) 9830415, 10023001

Solution. a) The whole number 503 is on the left of the whole number 530 on the num- ber line.

∴ 503 < 530.

b) The whole number 307 is on the left of the whole number 370 on the num- ber line.

∴ 307 < 370.

c) The whole number 56789 is on the left” of the whole number 98765 on the number line.

∴ 56789 < 98765

d) The whole number 10023001 is on the right of the whole number 9830415 on the number line.

∴ 10023001 > 9830415.

Question 8. Which of the following statements are true (T) and which are false (F)?

a) Zero is the smallest natural number.

Solution. False (F)

b) 400 is the predecessor of 399.

Solution. False (F)

c) Zero is the smallest whole number.

Solution. True (T)

d) 600 is the successor of 599.

Solution. True (T)

e) All natural numbers are whole numbers.

Solution. True (T)

f) All whole numbers are natural numbers.

Solution. False (F)

Number line representation of whole numbers HBSE

g) The predecessor of a two digit number is never a single digit number.

Solution. False (F)

h) 1 is the smallest whole number.

Solution. False (F)

i) The natural number 1 has no predecessor.

Solution. True (T)

j) The whole number 1 has no predecessor.

Solution. False (F)

k) The whole number 13 lies between 11 and 12.

Solution. False (F)

l) The whole number 0 has no predecessor.

Solution. True (T)

m) The successor of a two digit number is always a two digit number.

Solution. False (F)

Haryana Board Class 6 Maths Solutions For Chapter 2 Whole Numbers Very Short Answer Questions

Question 1. Which is the smallest whole number?

Solution. ‘0’ is the smallest whole number.

Question 2. Are all natural numbers whole numbers ?

Solution. Yes, all natural numbers are whole numbers because all natural numbers along with zero are called whole numbers.

Question 3. Are all whole numbers natural numbers ?

Solution. No, all whole numbers are not natural numbers. Except zero the remaining all whole numbers are natural numbers.

Question 4. How many whole numbers are there in between 27 and 46?

Solution. The whole numbers lie between 27 and 46 are 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45.

There are 18 whole numbers in between 27 and 46:

Question 5. Mark the smallest whole number on the number line.

Solution. The smallest whole number is zero (0).

Distributive property of whole numbers Class 6

Question 6. Choose the appropriate symbol form < or > and place it in the blanks.

1) 8 > 7

2) 5 > 2

3) 0 < 1

4) 10 > 5

Question 7. Present the successor of 11 and predecessor of 5 on the number line.

Solution. The successor of 11 is 12 and the predecessor of 5 is 4.

Haryana Board Class 6 Maths Solutions For Chapter 2 Whole Numbers Short Answer Questions

Question 8. Which of the statements are true (T) and which are false (F). Correct the false statements.

1) There is a natural number that has no predecessor.

Solution. True.

1 is a natural number that has no predecessor.

2) Zero is the smallest whole number.

Solution. True.

3) A whole number on the left of another number on the number line, is greater than that number.

Solution. False.

A whole number on the left of another number on the number line is smaller than that number.

Question 9. Show (1) 3+4 (2) 7-3 on number line.

1) 3+ 4

Solution. Consider 3 + 4

Start from 3. We add 4 to three. We make 4 jumps to the right on the number line as shown above then we will reach at 7

∴ 3 + 4 = 7

2) 7 – 3

Solution. Consider 7 – 3

Start from 7. Since we subtract 3 from 7 we take 3 steps to the left on the number line as shown above then we will reach 4.

∴ 7 – 3 = 4.

Question 10. Show (1) 5 x 2 (2) 4 x 3 on number line.

Solution. Consider 5 x 2 = 2 + 2 + 2 + 2 + 2

Start from 0. Move 2 units to the right each time, making 5 such moves we reach 10.

So, 5 x 2 = 10

2) 4 × 3

Solution. Consider 4 x 3 = 3 + 3 + 3 + 3

Start from 0. Move 3 units to the right each time, making 4 such moves we reach 12.

So, 4 x 3 = 12

Question 11. Find the sum of the predecessor of 300 and successor of 427.

Solution. The predecessor of 300 is 299.

The successor of 427 is 428.

∴ The required sum = 299 + 428

= 727

Haryana Board Class 6 Maths Solutions For Chapter 2 Whole Numbers Long Answer Questions

Question 12. Show these on number line:

1) 5+3

Answer.

5 + 3 = 8

2) 5 – 3

Answer.

5 – 3 = 2

Word problems on whole numbers for Class 6 HBSE

3) 3 + 5

Answer.

3 + 5 = 8

4) 10 + 1

Answer.

10 + 1 = 11

5) 8 – 5

Answer.

8 – 5 = 3

Question 13. Find the following using number line.

1) 6 + 7 + 7

Solution.

Start from 0, reach 6; we make 7 jumps from 6 to the right on the number line as shown above. We will reach 13.

Again start from 13, make 7 jumps to the right on the number line as shown above. We will reach 20.

6 + 7 + 7 = 20

2) 18 – 9

Solution.

Start from 0, reach 18. Since we subtract 9 from 18, Start from 18. We take 9 steps to the left on the number line as shown above. We will reach 9.

18 – 9 = 9

Identity elements in whole numbers Class 6

3) 5 x 3

Solution.

Start from 0, move 5 units to the right each time making 3 such moves. We will reach 15.

5 x 3 = 15

Haryana Board Class 6 Maths Solutions For Chapter 2 Whole Numbers Objective Type Questions

Choose the correct answer :

Question 1. Natural numbers are represented by

1. I
2. W
3. N
4. O

Answer. 3. N

Question 2. The successor of 16 is

1. 17
2. 15
3. 18
4. 16

Answer. 1. 17

Question 3. The predecessor of 25 is

1. 26
2. 25
3. 24
4. 27

Answer. 3. 24

Question 4. The smallest whole number is

1. 0
2. 1
3. 2
4. 3

Answer. 1. 0

Question 5. Which number has no predecessor in natural numbers?.

1. 0
2. 1
3. 2
4. 3

Answer. 2. 1

Question 6. ……. + 25 = 25

1. 1
2. 0
3. 2
4. 25

Answer. 2. 0

Question 7. The number just before a number is called.

1. Predecessor
2. Successor
3. Both A & B
4. None

Answer. 1. Predecessor

Question 8. The next number of any natural number is called.

1. Predecessor
2. Successor
3. Both A & B
4. None

Answer. 2. Successor

Question 9. The predecessor of the smallest natural number

1. 0
2. 1
3. 2
4. None

Answer. 4. None

Question 10. The successor of the greatest whole number

1. 0
2. 1
3. 100
4. cannot find

Answer. 4. cannot find

Question 11. Which of the following whole number does not have predecessor

1. 0
2. 1
3. 99
4. None

Answer. 1. 0

Question 12. Whole numbers are represented by

1. I
2. W
3. N
4. R

Answer. 2. W

Question 13. Additive identity of whole numbers is

1. 1
2. 2
3. -1
4. 0

Answer. 4. 0

Question 14. Multiplicative identity of whole numbers is

1. 1
2. 2
3. -1
4. 0

Answer. 1. 1

Question 15. Taking ‘2 steps four times’ represented by

1. 2 + 4
2. 4 + 2
3. 4 x 2
4. 2 × 4

Answer. 3. 4 x 2

Question 16. The sum of smallest natural number and smallest whole number is

1. 0
2. 1
3. 2
4. Not defined

Answer. 2. 1

Question 17. Division by zero is

1. 0
2. 1
3. same number
4. Not defined

Answer. 4. Not defined

Question 18. The sum of first 5 natural numbers

1. 14
2. 15
3. 16
4. 10

Answer. 2. 15

Question 19. The sum of first 5 whole numbers

1. 14
2. 15
3. 10
4. 16

Answer. 3. 10

Question 20. ……..+46 = 46

1. 1
2. 0
3. 46
4. 2

Answer. 2. 0

Question 21. Set of whole numbers

1. {1, 2, 3, 4,……}
2. {0,1,2,3,…………….}
3. {-3, -2, -1, 0, 1, 2, 3,…….}
4. None

Answer. 2. {0,1,2,3,…………….}

Question 22. Smallest whole number

1. 0
2. 1
3. -1
4. Not exist

Answer. 1. 0

Question 23. The predecessor of 1000 is

1. 1001
2. 999
3. 1000
4. 998

Answer. 2. 999

Question 24. The successor of 9999 is

1. 9998
2. 9999
3. 10000
4. 10001

Answer. 3. 10000

Question 25. Which number has no predecessor?

1. 1 in natural numbers
2. 0 in whole numbers
3. Both A & B
4. Neither A nor B

Answer. 3. Both A & B

Question 26. Which of the following represents the given number line?

4 + 2 = 6

4 x 2 = 8

2 × 4 = 8

10 – 2 = 8

Answer. 2. 4 x 2 = 8

Question 27. The difference of predecessor of 1000 and successor of 998 is……..

1

2

3

0

Answer. 4. 0

Chapter 2 Whole Numbers Fill in the blanks:

Question 28. The numbers 1, 2, 3 ….. which we use for counting are known as …………..

Answer. natural numbers

Question 29. The natural numbers along with the zero form the collection of ……… numbers.

Answer. whole

Question 30. The number just before a number is called the …………..

Answer. predecessor

Question 31. The next number of any natural number is called its …………

Answer. successor

Question 32. 3, 4 relation between these numbers is …………..

Answer. 4 > 3

Question 33. The sum of any two whole numbers is always a ………..

Answer. whole number

Question 34. …… by zero is not defined.

Answer. Division

Question 35. Every whole number has a ………

Answer. Successor

Question 36. We add …….. to a whole number we get the same whole number.

Answer. 0

Question 37. Every number can be arranged as a …………..

Answer. line

Question 38. ………… is the smallest whole number.

Answer. 0

Question 39. The number of whole numbers between 1 and 2 is ……..

Answer. 0

Question 40. 2021 ÷ 0 is ……..

Answer. Not defined

Question 41. ……. is the additive identiy.

Answer. 0

Haryana Board Class 7 Maths Solutions For Chapter 2 Fractions and Decimals

• Fraction: The numbers of the form \(\frac{a}{b}\), where a and b are whole numbers and b #0, are called “fractions”.
• Types of fractions:
  1. Proper fraction: In a proper fraction, the numerator is less than the denominator
     Examples: \(\frac{14}{19}, \frac{7}{9}, \frac{2}{3}, \frac{6}{13}, \frac{3}{4}\)
  2. Improper fraction: In an improper fraction, the .numerator is bigger than or equal to the denominator.
     Examples: \(\frac{9}{8}, \frac{7}{4}, \frac{21}{8}, \frac{35}{17}, \frac{43}{19}, \frac{4}{4}\)
  3. Mixed fraction: It is a combination of a whole number and a proper fraction
     Examples: \(1 \frac{3}{4}, 4 \frac{1}{9}, 5 \frac{6}{11}, 7 \frac{3}{4}, 3 \frac{4}{7}\)
     An improper fraction can be converted into a mixed fraction
     Examples: \(\frac{9}{8}=1 \frac{1}{8}\)
     \(\frac{21}{8}=2 \frac{5}{8}\)
  4. Fractions such as \(\frac{1}{2}, \frac{2}{4}, \frac{3}{6}\)…………. are called equivalent fractions
  5. ) Like fractions: Fractions with same denominators are called like fractions
     Examples: \(\frac{1}{7}, \frac{2}{7} ; \frac{3}{5}, \frac{2}{5}\)
  6.  Unlike fractions: Fractions with different denominators are called unlike fractions
     Examples: \( \frac{8}{9}, \frac{2}{7}, \frac{18}{17} \)……….
• Division of fractions: To divide a fraction with another fraction we multiply with its reciprocal.
• Example: \( \frac{2}{3} \div \frac{3}{4}=\frac{2}{3} \times \frac{4}{3}=\frac{8}{9} \)
• Decimal fractions or Decimal numbers:
• Fractions whose denominators are multiples of 10 only are called decimal fractions or decimal numbers.
  Example: \( 2.3=\frac{23}{10}, 0.47=\frac{47}{100} \text { etc. } \)
  Multiplication of decimal number by 10,100, 1000 etc.: When a decimal number is multiplied by16, 100, 1000 etc., the decimal point in the product shifts to the right as many zeros as in 10, 100, 1000 etc.
• We can change an improper fraction to . a mixedfraction and vice – versa.
• Multiplying a fraction with a whole number:
  To multiply a fraction with a whole number we multiply the whole number with the numerator and keeping the denominator same.
  Example: \( 2 \times \frac{7}{5}=\frac{14}{5} \)
• Product of two fractions \( =\frac{\text { Product of Numerators }}{\text { Product of Denominators }}\)Example: \(\frac{5}{6} \times \frac{2}{7}=\frac{5 \times 2}{6 \times 7}=\frac{10}{42}\)
• ‘of’ represents multiplication.
  Example: \(\frac{1}{2} \text { of } 3=\frac{1}{2} \times 3\)
• Reciprocal of a fraction: If \( \frac{a}{b} \) then \( \frac{b}{a}\) is called its reciprocal.
• A fraction means a part of a group of a region.
• Every fraction contains a numerator and a denominator
  Example: In \(\frac{4}{7}\) is the numerator and 7 is the denominator.

Solutions To Try These

1. Find:

Solution: \( \frac{2}{7} \times 3=\frac{2 \times 3}{7}=\frac{6}{7}\)

2. \( \frac{9}{7} \times 6\)

Solution:

3. \( 3 \times \frac{1}{8}\)

Solution:

HBSE Class 7 Fractions and Decimals Solutions

4. \( \frac{13}{11} \times 6\)

Solution:

2. Represent pictorially = \( 2 \times \frac{2}{5}=\frac{4}{5}\)

Exercise – 2.1

1) Which of the drawings (1) to (4) show:

1. \( 2 \times \frac{1}{5}\)

2. \( 2 \times \frac{1}{2}\)

3. \( 3 \times \frac{2}{3}\)

4. \( 3 \times \frac{1}{4}\)

Solution:

1-d
2-b
3-a
4-c

Haryana Board Class 7 Maths Fractions and Decimals solutions

2. Some pictures (a) to (c) are given below. Tell which of them show:

1. \( 3 \times \frac{1}{5}=\frac{3}{5}\)

2. \( 2 \times \frac{1}{3}=\frac{2}{3}\)

3. \( 3 \times \frac{3}{4}=2 \frac{1}{4}\)

Solution:

1. \( 3 \times \frac{1}{5}=\frac{3}{5}=(\mathrm{c})\)

2. \( 2 \times \frac{1}{3}=\frac{2}{3}=(a)\)

3. \( 3 \times \frac{3}{4}=2 \frac{1}{4}=(b)\)

HBSE 7th Class Fraction and Decimal Word Problems – Focuses on word problems in this chapter.

3. Multiply and reduce to lowest form and convert into a mixed fraction:

1. \( 7 \times \frac{3}{5}\)

Solution: \( 7 \times \frac{3}{5}=\frac{7 \times 3}{5}=\frac{21}{5}=4 \frac{1}{5}\)

2. \( 4 \times \frac{1}{3}\)

Solution: \( 4 \times \frac{1}{3}=\frac{4 \times 1}{3}=\frac{4}{3}=1 \frac{1}{3}\)

3. \( 2 \times \frac{6}{7}\)

Solution:\( 2 \times \frac{6}{7}=\frac{2 \times 6}{7}=\frac{12}{7}=1 \frac{5}{7}\)

4.\( 5 \times \frac{2}{9}\)

Solution:\( 5 \times \frac{2}{9}=\frac{5 \times 2}{9}=\frac{10}{9}=1 \frac{1}{9}\)

5. \( \frac{2}{3} \times 4\)

Solution:\( \frac{2}{3} \times 4=\frac{2 \times 4}{3}=\frac{8}{3}=2 \frac{2}{3}\)

6.\( \frac{5}{2} \times 6\)

Solution:\( \frac{5}{2} \times 6=\frac{5 \times 6}{2}=\frac{30}{2}=15\)

7. \( 11 \times \frac{4}{7}\)

Solution:\( 11 \times \frac{4}{7}=\frac{11 \times 4}{7}=\frac{44}{7}=6 \frac{2}{7}\)

8. \( 20 \times \frac{4}{5}\)

Solution:\( 20 \times \frac{4}{5}=\frac{20 \times 4}{5}=\frac{80}{5}=16\)

9.\( 13 \times \frac{1}{3}\)

Solution: \( 13 \times \frac{1}{3}=\frac{13 \times 1}{3}=\frac{13}{3}=4 \frac{1}{3}\)

10.\( 15 \times \frac{3}{5}\)

Solution:\( 15 \times \frac{3}{5}=\frac{15 \times 3}{5}=\frac{45}{5}=9\)

4. Shade:

1. \( \frac{1}{2}\) of the circles in box (1)

2. \( \frac{2}{3}\) of the trianglesin box (2)

3. \( \frac{3}{5}\) of the squares in box (3)

1) 

2)

Sample Problems Fractions and Decimals Haryana Board Class 7

3)

Addition and subtraction of fractions Class 7 HBSE

Solution:

1)

2)

3)

5. Find:

1) \( \frac{1}{2}\) of (1) 24 (2) 46

Solution: (1) \( \frac{1}{2}\) of 24 =\( \frac{1}{2} \times 24\)\( =\frac{1 \times 24}{2}=\frac{24}{2}=12\)

(2)\( \frac{1}{2} \text { of } 46=\frac{1}{2} \times 46\)

\( =\frac{1 \times 46}{2}=\frac{46}{2}=23\)

2)\( \frac{2}{3}\) of (1) 18 (2) 27

Solution:

1)\( \frac{2}{3}\) of 18 \( =\frac{2}{3} \times 18=\frac{2 \times 18}{3}=\frac{36}{3}=12 \)

(2)\( \frac{2}{3} \text { of } 27=\frac{2}{3} \times 27\)

3) \( \frac{3}{4}\) of (1) 16 (2) 36

Solution:

(1)\( \frac{3}{4} \text { of } 16=\frac{3}{4} \times 16=\frac{3 \times 16}{4}=\frac{48}{4}=12\)

(2)\( \frac{3}{4} \text { of } 36=\frac{3}{4} \times 36\)

4. \( \frac{4}{5} \) of (1) 20 (2) 35

Solution:

(1)\( \frac{4}{5} \text { of } 20=\frac{4}{5} \times 20=\frac{4 \times 20}{5}=\frac{80}{5}=16 \)

(2) \( \frac{4}{5} \text { of } 35=\frac{4}{5} \times 35 \)

6. Multiply and express as a mixed fraction:

1) \( 3 \times 5 \frac{1}{5} \)

Solution:

2) \( 5 \times 6 \frac{3}{4} \)

Solution:

3) \( 7 \times 2 \frac{1}{4} \)

Solution: \( 7 \times 2 \frac{1}{4}=7 \times\left(\frac{2 \times 4+1}{4}\right) \)

4) \( 4 \times 6 \frac{1}{3} \)

Solution: \( 4 \times 6 \frac{1}{3}=4 \times\left(\frac{6 \times 3+1}{3}\right) \)

5) \( 3 \frac{1}{4} \times 6 \)

Solution: \( \left(\frac{3 \times 4+1}{4}\right) \times 6=\left(\frac{12+1}{4}\right) \times 6 \)

Multiplying and Dividing Fractions Class 7 Haryana Board

6) \( 3 \frac{2}{5} \times 8 \)

Solution: \( \left(\frac{3 \times 5+2}{5}\right) \times 8=\left(\frac{15+2}{5}\right) \times 8 \)

7) Find:

1) \( \frac{1}{2} of \) (1) \( 2 \frac{3}{4} \) (2)\( 4 \frac{2}{9} \)

Solution:

(1) \( \frac{1}{2} \text { of } 2 \frac{3}{4}=\frac{1}{2} \times\left(\frac{2 \times 4+3}{4}\right) \)

(2) \( \frac{1}{2} \text { of } 4 \frac{2}{9}=\frac{1}{2} \times\left(\frac{4 \times 9+2}{9}\right) \)

Multiplication and division of decimals Class 7 HBSE

2) \( \frac{5}{8} \) of (1) \( 3 \frac{5}{6} \) (2) \( 9 \frac{2}{3} \)

Solution:

(1) \( \frac{5}{8} \text { of } 3 \frac{5}{6} \)

(2) \( \frac{5}{8} \text { of } 9 \frac{2}{3} \)

8) Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained 5 litres of water. Vidya consumed \( \frac{2}{5} \) of the water. Pratap consumed the remaining water

(1) How much water did Vidya drink?

(2) What fraction of the total quantity of water did Pratap drink?

Solution:

Quantity of water in the bottle = 5 litres

(1) Water consumed by Vidya = \( \frac{2}{5} \) of 5 litres

(2) Water consumed by Pratap = \( \frac{1}{1}-\frac{2}{5} \)

Solutions To Try These

Find:

1. \( 7 \div \frac{2}{5} \)

Solution: \( 7 \div \frac{2}{5}=7 \times \frac{5}{2}=\frac{7 \times 5}{2}=\frac{35}{2}=17 \frac{1}{2} \)

2. \( 6 \div \frac{4}{7} \)

Solution: \( \begin{aligned}
6 \div \frac{4}{7} & =6 \times \frac{7}{4}=\frac{6 \times 7}{4} \\
& =\frac{42}{4}=\frac{42 \div 2}{4 \div 2}=\frac{21}{2}=10 \frac{1}{2}
\end{aligned} \)

3. \( 2 \div \frac{8}{9} \)

Solution: \( \begin{aligned}
2 \div \frac{8}{9}=2 \times \frac{9}{8} & =\frac{2 \times 9}{8}=\frac{18}{8}=\frac{18 \div 2}{8 \div 2} \\
& =\frac{9}{4}=2 \frac{1}{4}
\end{aligned} \)

Solutions To Try These

Find:

1. \( 6 \div 5 \frac{1}{3} \)

Solution: \( \begin{aligned}
6 \div 5 \frac{1}{3} & =6 \div \frac{16}{3}=6 \times \frac{3}{16}=\frac{6 \times 3}{16} \\
& =\frac{18}{16}=\frac{18 \div 2}{16 \div 2}=\frac{9}{8}=1 \frac{1}{8}
\end{aligned} \)

2. \( 7 \div 2 \frac{4}{7} \)

Solution:

HBSE Class 7 Maths Chapter 2 Guide

Solutions To Try These

Find:

1. \( \frac{3}{5} \div \frac{1}{2} \)

Solution: \( \frac{3}{5} \div \frac{1}{2}=\frac{3}{5} \times \frac{2}{1}=\frac{3 \times 2}{5 \times 1}=\frac{6}{5}=1 \frac{1}{5} \)

2. \( \frac{1}{2} \div \frac{3}{5} \)

Solution:

3. \( 2 \frac{1}{2} \div \frac{3}{5} \)

Solution:

4. \( 5 \frac{1}{6} \div \frac{9}{2} \)

Solution:

Exercise 2.3

1. Find:

1. \( 12 \div \frac{3}{4} \)

Solution:

2. \( 14 \div \frac{5}{6} \)

Solution:

3. \( 8 \div \frac{7}{3} \)

Solution:

4. \( 4 \div \frac{8}{3} \)

Solution:

5. \( 3 \div 2 \frac{1}{3} \)

Solution:

Important Concepts Fractions and Decimals Class 7 HBSE

6. \( 5 \div 3 \frac{4}{7} \)

Solution:

2. Find the reciprocal of each of the following fractions. Classify the reciprocal as proper fraction,improper fraction and whole numbers.

1) \( \frac{3}{7} \)

Solution: \( \text { Reciprocal of } \frac{3}{7} \text { is } \frac{7}{3} \)

Word problems on fractions and decimals Class 7 HBSE

2) \( \frac{5}{8} \)

Solution: \( \text { Reciprocal of } \frac{5}{8} \text { is } \frac{8}{5} \)

3) \( \frac{9}{7} \)

Solution: \( \text { Reciprocal of } \frac{9}{7} \text { is } \frac{7}{9} \)

4) \( \frac{6}{5} \)

Solution: \( \frac{12}{7} \)

5) \( \frac{12}{7} \)

Solution:

6) \( \frac{1}{8} \)

Solution: \( \text { Reciprocal of } \frac{1}{8} \text { is } \frac{8}{1}=8 \)

∴ 8 is a whole number

7) \( \frac{1}{11} \)

Solution:

∴ 11 is a whole number.

3. Find:

1) \( \frac{7}{3} \div 2 \)

Solution:

2) \( \frac{4}{9} \div 5 \)

Solution:

3) \( \frac{6}{13} \div 7 \)

Solution:

4) \( 4 \frac{1}{3} \div 3 \)

Solution:

5) \( 3 \frac{1}{2} \div 4 \)

Solution:

6) \( 4 \frac{3}{7} \div 7 \)

Solution:

4. Find:

1) \( \frac{2}{5} \div \frac{1}{2} \)

Solution:

2) \( \frac{4}{9}+\frac{2}{3} \)

Solution:

3) \( \frac{3}{7} \div \frac{8}{7} \)

Solution:

4) \( 2 \frac{1}{3} \div \frac{3}{5} \)

Solution:

5) \( 3 \frac{1}{2} \div \frac{8}{3} \)

Solution:

6) \( \frac{2}{5} \div 1 \frac{1}{2} \)

Solution:

7) \( 3 \frac{1}{5} \div 1 \frac{2}{3} \)

Solution:

8) \( 2 \frac{1}{5} \div 1 \frac{1}{5} \)

Solution:

1. Find:

1) 2.7×4

Solution: 2.7×4 = 10.8

2) 1.8 x 1.2

Solution: 1.8 x 1.2 = 2.16

3) 2.3 x 4.35

Solution: 2.3 x 4.35 = 10.005

2. Arrange the products obtained in (1) in descending order.

Solution:

The three products obtained in (1) are

10.8, 2.16,10.005. Their descending order is 10.8,10.005,2.16.

Solutions To Try These

Find:

1) 0.3 x 10

Solution: 0.3 x l0 = 3

2) 1.2×100

Solution: 1.2 x100 = 1.20 x100 = 120

3) 56.3 x1000

Solution: 56.3 x1000 = 56.300 x1000 = 56300

Exercise -2.4

1. Find:

1) 0.2 x 6

Solution: 0.2 x 6 = 1.2

2) 8 x 4.6

Solution: 8×4.6 = 36.8

3) 2.71 x 5

Solution: 2.71 x 5 = 13.55

4) 20.1 x 4

Solution: 20.1 x 4 = 80.4

5) 0.05 x 7

Solution: 0.05×7 = 0.35

6) 211.02×4

Solution: 211.02 x4 = 844.08

7) 2x 0.86

Solution: 2×0.86 = 1.72

2. Find the area of rectangle whose length is 5.7 cm and breadth is 3 cm.

Solution:

Length of the rectangle = 5.7 cm

Breadth of the rectangle = 3 cm

Area of the rectangle = Length x Breadth

= 5.7 cm x 3 cm = 17.1 cm2

3. Find:

1) 1.3 x 10

Solution: 1.3 x 10 = 13.0 or 13

2) 36.8 x 10

Solution: 36.8 x10 = 368.0 or 368

3) 153.7 x 10

Solution: 153.7 x 10 = 1537.0 or 1537

4) 168.07 x 10

Solution: 168.07 x 10 = 1680.7

5) 31.1 x 100

Solution: 31.1 x100 = 3110

6) 156.1 xl00

Solution: 156.1 x100 = 15610

7) 3.62 x 100

Solution: 3.62 x 100 = 362

8) 43.07 x100

Solution: 43.07 x 100 = 4307

9) 0.5 x 10

Solution: 0.5 x10 = 5

10) 0.08 x 10

Solution: 0.08 x 10 = 0.80 or 0.8

11) 0.9 x 100

Solution: 0.9 x 100 = 90.0 or 90

12) 0.03 x 1000

Solution: 0.03 x 1000 = 30.0 or 30

How to convert fractions to decimals Class 7

4. A two-wheeler covers a distance of 55.3 km with one litre of petrol. How much distance will it cover in 10 litres of petrol ?

Solution:

Distance covered with one litre of petrol = 55.3 km

Distance covered with10litres of petrol = 55.3 x10 = 553 km

5. Find:

1) 2.5 x 0.3

Solution: 2.5 x 0.3 = 0.75

2) 0.1 x 51.7

Solution: 0.1 x 51.7 = 5.17

3) 0.2 x 316.8

Solution: 0.2 x 316.8 = 63.36

4) 1.3 x 3.1

Solution: 1.3×3.1=4.03

5) 0.5 x 0.05

Solution: 0.5 x 0.05 = 0.025

6) 11.2 x 0.15

Solution: 11.2 x 0.15 =1.680

7) 1.07 x. 0.02

Solution: 1.07 X 0.02 = 0.0214 .

8) 10.05 x 1.05

Solution: 10.05 x 1.05 = 10.5525

9) 101.01 x 0.01

Solution: 101.01 x 0.01 = 1.0101

10) 100.01 x 1.1

Solution: 00.01 x 1.1 = 110.011

Solutions To Try These

1. Find:

1) 235.4 – 10

Solution: 235.4 + 10 = 23.54

2) 235.4 +100

Solution: 235.4 = 2.354

3) 235.4 +1000

Solution: 235.4 +1000 = 0.2354

2. Find:

1) 35.7 +3 = ?

Solution: 35.7+3 = 11.9

2) 25.5 +3 =?

Solution: 25.5 +3 = 8.5

Practice Problems Fractions and Decimals Class 7 Haryana Board

3. Find:

1) 43.15+5 = ?

Solution: 43.15 +5 = 4315 +5 = 863

43.15 +5 = 8.63

2) 82.44 +6 =?

Solution: 8244 + 6 = 1374

82.44 + 6 = 13.74

Solutions To Try These

1. Find:

1) 15.5+5

Solution: 155 +5=31

15.5 +5 = 3.1

2) 126.35 +7

Solution: 12635 + 7 = 1805

126.35 +7 = 18.05

2. Find:

1. \( \frac{7.75}{0.25} \)

Solution:

2. \( \frac{42.8}{0.02} \)

Solution:

3) \( \frac{5.6}{1.4} \)

Solution: \( \frac{5.6}{1.4}=\frac{5.6 \times 10}{1.4 \times 10}=\frac{56}{14}=4 \)

Exercise – 2.5

1. Find:

1. 0.4 ÷ 2

Solution:

2) 0.35 ÷ 5

Solution:

3) 2.48 ÷ 4

Solution:

4) 65.4 ÷ 6

Solution:

5) 651.2 ÷ 4

Solution:

6) 14.49 ÷ 7

Solution:

7) 3.96 ÷ 4

Solution:

8) 0.80 ÷ 5

Solution:

2. Find:

1) 4.8 ÷ 10

Solution:

2) 52.5 ÷ 10

Solution:

3) 0.7 ÷ 10

Solution:

4) 33.1 ÷ 10

Solution: