Reflection Of Waves

If a moving surface wave on water strikes a wall, it is found that another wave starts moving along the surface of water in the opposite direction. Again, standing at a certain distance from a large wall if a loud sound is made, a similar sound comes back to our ears after a while.

• We know that if light falls on a mirror, it changes its direction. These phenomena are examples of the reflection of waves, though the nature of the waves are different in different cases.
• We know that the direction along which the energy of a wave is transferred is called a ray. It is represented by an arrowheaded straight line. Suppose, a ray travels through a medium and is incident at a point on an interface with another medium.
• This point is called the point of incidence. The ray striking the interface is called the incident ray. The ray returning to the first medium from the point of incidence after reflection is called the reflected ray.
• PQ is the interface of two media or a reflector, O is the point of incidence, and AO and OB are incident ray and reflected ray, respectively. The perpendicular ON on the reflector drawn at the point of incidence O is called the normal.

The angle between the incident ray and the normal is called the angle of incidence. Similarly, the angle between the reflected ray and the normal is called the angle of reflection.

Reflection Of Waves Class 11 Important Questions

Laws of reflection of light: Reflection of waves obeys two laws. These are known as the laws of reflection.

1. The incident ray, the reflected ray, and the normal to the reflector at the point of incidence lie on the same plane.
2. The angle of incidence is equal to the angle of reflection, i.e., i = r.

Reflection Of Sound Definition: Sound propagates in the form of waves from one place to another. So, like other waves sound also exhibits the phenomenon of reflection.

Reflection Of Sound Experimental Demonstration:

Plane Reflector Definiton: A plane reflector R is placed vertically on a horizontal table. A tall partition P perpendicular to the reflector at O divides the table into two halves. Two tubes A and B are placed on the table in such a way that their axes are directed to O and they make equal angles with OP (i.e., ∠AOP = ∠BOP).

• Now, if a source of sound (for example, a table clock) is placed in front of tube A and a receiver (for example, an ear) is placed in front of tube B, the sound of the clock is heard distinctly.
• Due to the partition in the middle, the sound of the clock cannot reach the ear directly rather after being reflected at O of the reflector it reaches the receiver, i.e., the ear. If ∠BOP is changed a little by rotating the axis of the tube B or by raising the tube from the table slightly, sound is not heard anymore.

From this experiment, it is evident that

1. Sound has been reflected from the reflector,
2. The angle of incidence is equal to the angle of reflection and
3. The incident ray, the reflected ray, and the normal at the point of incidence lie in the same plane (plane of the table).

Reflection Of Waves Class 11 Notes

Concave Reflector: Two concave reflectors A and B are placed in such a way that their axes lie on fee same straight line. A source of sound (for example, a table clock) is placed at the focus of A.

The sound waves produced by the clock get rejected from fee reflector A and propagate parallel to the axis. These parallel waves are Incident on the reflector B and again get reflected from Its surface. They meet at fee frees, of 3, If we place our ear there, a distinct sound is heard.

Size Of The Reflector: To obtain an effective reflection of a wave from a reflector, the fee size it should be much greater than a feat of the wavelength. The wavelength of audible sound in air varies from 1.5 cm to 16 m. On the other hand, the wavelength of visible light varies from 4 x 10^-7 m to 8 x 10^-7 m, ie., a sound wave is much longer than a light wave. So tight can be reflected from very small reflectors, but for reflection of sound the size of the fee reflector should be very large.

• Regular reflection of waves takes place from a smooth reflector. If the surface of the reflector is rough, diffused reflection takes place. Whether a surface is smooth or rough is known from fee knowledge of fee wavelength. For example, a large wall may look smooth to the naked eye, but it has many fine notches.
• However, these notches are much smaller than the wavelength of sound. So in case of reflection of sound, a large wall may be taken as a smooth reflector, and regular reflection of sound takes place from it. On the other hand, fee notches of that wall are many times larger than the wavelength of light, and hence, light suffers diffused reflection from the wall.

Reflection Of Waves Class 11 Physics

In short, it may be said feat, to get a regular reflection of sound,

1. Fee reflector must be large enough and
2. The surface of the reflector need not be very smooth.

So buildings, long walls, mountains, rows of trees, etc., act as reflectors of sound.

Wave Motion Refraction Of Waves

When a progressive wave travelling in a homogeneous medium meets a surface of separation with another homogeneous medium, a part of the incident wave is transmitted into fee second medium. This phenomenon is known as the refraction of waves. In refraction, generally, the direction of wave motion changes while the waves cross the interface of two media.

If nearly all of the energy carried by the incident wave enters the second medium, the second medium is called a transparent medium. For light waves, air, water, glass, etc., are transparent media.

• On the other hand, if a negligible portion of the energy enters the second medium, the second medium is called an opaque medium. For light waves, wood, iron, brick walls, etc., are opaque media. Between them, ground glass, oily paper, etc., are semitransparent media.

PQ: Surface of separation of two media or the refracting surface

AO: Incidentally

O: Point of incidence

OB: Refracted ray i.e. the ray entering the 2nd medium.

MN: normal at the point of incidence on the refracting surface

∠AOM = i = angle of incidence

∠BON = r = angle of refraction

Reflection Of Waves At A Boundary Class 11

Laws Of Refraction Of light: Refraction of waves obeys the following two laws:

1. The incident ray, the refracted ray, and the normal to the refracting surface at the point of incidence lie on the same plane.
2. The ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant. The magnitude of the constant depends on the nature of the two media and the color of the incident wave.

Mathematically, \(\frac{\sin i}{\sin r}={constant}\left({ }_1 \mu_2\right)\)

where i and r are the angle of incidence and the angle of refraction, respectively, and μ is called the refractive index of the second medium with respect to the first medium. The second law of refraction is known as Snell’s Law.

The refractive index (₁μ₂) is also equal to the ratio of the wave velocities in the two media, i.e., \({ }_1 \mu_2=\frac{v_1}{v_2}; v_1\) and v₂ are respectively the velocities of die waves in the first and the second medium. The medium with a smaller wave velocity is called a denser medium and the medium with greater wave velocity is called a rarer medium.

Rule governing the deviation of a ray: Generally, the direction of wave motion changes at the time of crossing the refracting surface, i.e., the ray changes its direction. The rule of deviation is as follows:

1. When a ray enters a denser medium from a rarer one, the refracted ray bends towards the normal. In this case, the angle of refraction is less than the angle of incidence, i.e., r< i. Clearly, the second medium is denser than the first medium.
2. When a ray enters a rarer medium from a denser one, the refracted ray bends away from the normal. In this case, the angle of refraction is greater than the angle of incidence, i.e., r> i.

Relation between incident and refracted waves

1. Due to refraction, the frequency and the time period of waves do not change.
2. The wavelength and the wave velocity suffer changes during refraction.
3. The phase of the wave does not change during refraction, i.e., the phase difference between the incident wave and the refracted wave is zero.

In this chapter, only the phenomenon of refraction of sound will be discussed.

Reflection Of Mechanical Waves Class 11

Refraction Of Sound Waves : John Tyndall was the first to demonstrate refraction of sound through a balloon filled with carbon dioxide (CO₂). The balloon, surrounded by air, behaves like a convex lens of glass surrounded by air for refraction of light.

• This is because carbon dioxide is heavier than air. If a clock is placed on one side of the balloon, the sound rays produced by the clock meet at a particular point on the other side after refraction through the balloon.
• If we place our ears at that point, the sound of the clock is heard distinctly. But sound will not be heard if we place our ears elsewhere.
• It is an important point to note that, the velocity of sound in air is nearly 330 m · s^-1, whereas that in water is about 1500 m · s^-1. As a consequence, unlike in the case of light waves, air is a medium denser than water for sound waves. So, when sound enters water from the air, the rays deviate away from the normal.

Steel is a still rarer medium, as the velocity of sound in it is about 5000 m · s^-1. A convex-shaped steel lens or water lens placed in air would, thus, show the properties of a concave lens, i.e., would behave as a diverging lens.

Refraction Of Sound In The Atmosphere

Effect Of Temperature: The whole atmosphere over the surface of the earth may be supposed to be divided into layers, one above the other. At daytime, the layer of air adjacent to the surface of the earth has the highest temperature and as we move upwards the temperature falls gradually.

• So, the density of air increases with the increase of height from the surface of the earth. Thus, the upper layers of air are denser than the layers near the surface of the earth. Hence, the sound emitted from a source near the surface of the earth gets refracted.
• While propagating upwards due to refraction, it bends towards the normal at every layer and eventually travels upwards almost vertically. For this reason, only a negligible portion of the sound emitted from the source reaches a distant listener standing on the surface of the earth, i.e., at day time sound cannot travel a large distance in the forward direction.

Reflection And Transmission Of Waves Class 11

Just the opposite happens m night, The density of the lowermost layer of air is maximum because its temperature is minimum. So, sound omitted from a source on the surface of the earth gets refracted while propagating upwards. In this case, sound moves from a denser to a rarer medium.

• So it bends away from the normal at every layer, At one stage, total internal reflection occurs and it begins to move downwards. Ultimately, it reaches a listener.
• So, the sound emitted from a distant source can be heard distinctly at night.
• Sound of a distant train, low voices of persons sitting in a boat floating in the middle of a river, etc., are very clear to our ears at night.

Numerical Problems On Reflection Of Waves Class 11

Effect Of Wind: Generally, the velocity of wind near the surface of the earth is less than that in the upper layers. If the wind blows from the source to the listener, the wavefronts at the lower levels have comparatively smaller velocities.

Hence, the wavefronts bend towards the earth and help the listener to hear the sound. So, under this condition, the sound coming from a distant source is heard distinctly.

• On the other hand, if the wind blows in the opposite direction, i.e., from the listener to the source, an opposite incident happens. In this case, the wavefronts at the upper levels have comparatively smaller velocities.
• Hence, the wavefronts bend in the upward direction. So a very negligible portion of the sound can reach a distant listener standing on the surface of the earth. Therefore, under this condition, the sound coming from a distant source is not heard distinctly.

Wave Motion Echo

Definition Of Echo: We know from practical experiences that the sound produced by drums, crackers, gunshots, etc., reaches our ears directly, and also produces echoes after getting reflected from faraway buildings, trees, etc.

Echoes are distinct only when the distance between the listener and the reflecting surface is sufficiently large to allow the reflected sound to reach the listener without overlapping with the original sound.

Minimum Distance Of The Reflector

Inarticulate Sound: Echoes are produced due to the reflection of sound. But all reflected sounds cannot produce an echo. When we hear an inarticulate sound, its sensation persists in our ear for about \(\frac{1}{10}\)th of a second.

• This is known as the persistence of hearing. So to distinguish echo from the original sound, at least \(\frac{1}{10}\)th of a second should be elapsed between the production of sound and the arrival of the reflected sound in the ear-this is the condition required to hear an echo of inarticulate sound.
• We know that the velocity of sound at 0°C in air is about 330 m · s^-1. So, distance travelled by sound in \(\frac{1}{10}\)s is 330 x \(\frac{1}{10}\) = 33 m. Hence, in order to hear an echo, the minimum distance between the reflecting surface and the listener should be \(\frac{33}{2}\) = 16.5 m = 54 ft. This calculation is valid for inarticulate sounds, like the sound produced by a gunshot, clapping, etc.
• If the distance of the reflector from the listener is less than 16.5 m or 54 ft, sound takes less than \(\frac{1}{10}\)s to come back to the listener after reflection. So, the listener cannot distinguish between the original sound and the reflected one, i.e., the echo is not heard. For this reason, echo is not audible in a room of ordinary size.

Wave Motion And Echo Class 11 Notes

Articulate Sound: To hear an echo of articulate sound, the minimum distance between the reflector and the listener is greater. This is due to the fact that a man cannot distinctly pronounce more than 5 syllables in one second. Our ears also cannot recognize separately more than 5 syllables in one second.

• So, for monosyllabic sound, the time interval between the original sound and its echo must not be less than \(\frac{1}{5}\)s During this time, sound travels (330 x \(\frac{1}{5}\)) or 66 m.
• This distance is again twice the distance between the listener and the reflector. So the minimum distance of the listener from the reflector should be \(\frac{66}{2}\) = 33 m, for bearing the echo of a monosyllabic word. For a disyllabic word, the distance should be 2 x 33 = 66 m, and so on.

Wave Motion Class 11 Physics Notes

Multiple Echoes: When a sound is reflected from a number of suitably placed reflecting surfaces, a number of echoes may be heard. Minimum \(\frac{1}{10}\)s of time interval is required between die original sound and the first echo and also between any two successive echoes that reach our ears.

The rumbling and rolling of under is really caused by multiple reflections from cloud surfaces. Successive reflections may also be produced between two reflecting surfaces suitably placed.

Reverberation: It is often noted that when a loud sound is produced near the walls of a big hall, it returns after reflection very quickly (i.e., the time interval is less than \(\frac{1}{10}\)s) when the effect of the original sound still persists. On account of successive reflections from the walls, a continuous rolling of sound goes on for some time. This persistence of sound due to multiple reflections from the walls is called reverberation.

• This effect is not at all desirable sometimes, because the original sound cannot be recognized distinctly. This effect is minimized by increasing the absorption of sound at the walls by carpeting them with sound-absorbing substances.
• It is obvious that if there are multiple reflectors, either echo or reverberation of sound will be produced. If the time interval between successive sounds is greater than \(\frac{1}{10}\)s, the echo will be heard; if the time interval is less than \(\frac{1}{10}\) s, reverberation will be heard.

Echo Formula And Examples Class 11 Physics

Practical Applications Of Echo:

1. Measurement Of A Distance: The distance of a distant hill or of any extended reflector can be determined with the help of an echo. In this case, a sharp inarticulate sound, like the sound of a gunshot, is produced, and simultaneously a stopwatch is Started. The stopwatch is stopped just on hearing the echo from the distant reflector.

Let the distance of the reflector from the place of the experiment be D, the time interval between the original sound and the echo heard be t, and the velocity of sound In air be V.

∴ Distance traveled by sound = Vt

Since sound travels the distance D and again returns to the place of experiment, the total distance traveled Is 2D.

∴ 2D = Vt or, D = \(\frac{Vt}{2}\)

Knowing the velocity of sound in air (V) and the time (t) from the stopwatch, the distance (D) of the reflector can be determined.

Echo In Wave Motion Class 11

2. Measurement Of The Depth Of A Sea: The depth of a sea can be measured with the help of an echo. A source S containing some explosive material is kept at a depth h from one end of a ship and a hydrophone H (an underwater microphone) is kept immersed at the same depth h from the other end. A loud sound is produced due to the explosion at S. Sound can reach the hydrophone along two paths

1. Straight line path sh and
2. Path soh after reflection from the bottom O of the sea.

The sound that reaches along SH is called original sound and the sound that reaches along SOH is called reflected sound. The hydrophone electrically records the time intervals in which sound travels along the direct path SH, as well as along the reflected path SOH.

Let the velocity of sound in water be V, the depth of the source and the hydrophone from the surface of the sea be h, the depth of the sea with respect to the source or the hydrophone be NO = d, time taken by the sound to reach the hydrophone directly be t₁, and time taken by the echo be t₂.

According to the figure, SH = \(V t_1 \text {, i.e., } S N=\frac{V t_1}{2}\)

Again, SO + OH = Vt₂

or, \(S O=\frac{V t_2}{2}\) [because SO=OH]

∴ d = ON = \(\sqrt{S O^2-S N^2}=\sqrt{\left(\frac{V t_2}{2}\right)^2-\left(\frac{V t_1}{2}\right)^2}\)

= \(\frac{V}{2} \sqrt{t_2^2-t_1^2}\)

So, the depth of the sea from its surface is,

D = h + d = \(h+\frac{V}{2} \sqrt{t_2^2-t_1^2}\) .

So if V is known, the depth D of the sea can be determined.
If the depth of the sea is very large, the length of the path SH is very small compared to the path SOH. So, t₁ may be neglected relative to t₂, and h may be neglected relative to d,

i.e., in that case, D = \(\frac{V t_2}{2}.\)

This method is called echo depth ranging or SONAR (Sound Navigation And Ranging).

Conditions For Echo Class 11 Physics

3. Measurement Of The Altitude Of An Airplane: The altitude of a flying airplane can also be measured with the help of an echo. Let us consider an airplane flying horizontally at a height h along the path AB with a velocity v as shown.

When the plane is at A, a loud sound is produced and the echo is heard after time t when the plane is at B. So, sound reflects from the ground at point O and reaches the airplane along the path AOB, where AO = OB.

Let the velocity of the plane be v, the velocity of sound in air be V, and the time interval between the original sound and the echo be t.

∴ Distance traveled by the plane = AB = vt

i.e., AN = \(\frac{v t}{2}\) [AN = NB]

Again, the distance travelled by the sound is AO + OB = Vt

i.e., AO = \(\frac{v t}{2}\) [AO = OB]

So, the altitude of the plane,

h = \(O N=\sqrt{A O^2-A V^2}=\sqrt{\left(\frac{V t}{2}\right)^2-\left(\frac{v t}{2}\right)^2}=\frac{t}{2} \sqrt{V^2-v^2}\)

Therefore, knowing v, V, and t, the altitude h of the plane can be determined from the above equation.

Class 11 Physics Unit 10 Oscillation And Waves Chapter 3 Wave Motion Echo Numerical Examples

Example 1. A shell is fired from a motor boat moving along the I surface of a sea with a speed of 60 km · h^-1 towards j the shore. The echo of the firing is heard in the motor, boat after 9s. What was the distance of the boat from the shore at the time of firing? The velocity of sound = 330 m · s^-1.
Solution:

Given

A shell is fired from a motor boat moving along the I surface of a sea with a speed of 60 km · h^-1 towards j the shore. The echo of the firing is heard in the motor, boat after 9s.

Distance travelled by sound in 9 s = 330 x 9 = 2970 m

Now, \(60 \mathrm{~km} \cdot \mathrm{h}^{-1}=\frac{60 \times 1000}{60 \times 60} \mathrm{~m} \cdot \mathrm{s}^{-1}=\frac{50}{3} \mathrm{~m} \cdot \mathrm{s}^{-1}\)

So, the distance traveled by the motor boat in 9 s is, = \(\frac{50}{3}\) x 9 = 150 m

If the distance of the shore at the time of firing is xm, then the sound of firing moves x m and then returns (x-150) m after reflection from the shore.

So, x+(x- 150) =2970

or, 2x = 2970 + 150 or, 2x = 3120 or, x = 1560

So, the distance of the motor boat from the shore at the time of firing is 1560 m or 1.56 km.

Derivation Of Echo Formula Class 11

Example 2. What should be the minimum distance of a reflector to hear the echo of a tetrasyllable word? Velocity of sound= 330 m · s^-1.
Solution:

The minimum time interval required between the original sound and the echo of a tetrasyllabic word = 4 x \(\frac{1}{5}\) = \(\frac{4}{5}\)s.

∴ Minimum required distance = \(\frac{330 \times 4 / 5}{2}=132 \mathrm{~m}\)

Velocity Of Sound And Echo Class 11 Physics

Example 3. A man Is approaching a hill with a velocity of 5 m · s^-1. He fires a gun when he is 3 km away from the hill. When and where will he listen to the echo? The velocity of sound = 355 m · s^-1.
Solution:

Given

A man Is approaching a hill with a velocity of 5 m · s^-1. He fires a gun when he is 3 km away from the hill.

3km = 3000m

Let us consider that the man advances x m after firing the gim and before hearing the echo.

Time required for this purpose, t = \(\frac{x}{5}\) s

Distance travelled by sound in that time = 3000 +(3000-x) = (6000 -x) m

∴ t = \(\frac{6000-x}{355} \mathrm{~s}\)

i.e., \(\frac{x}{5}=\frac{6000-x}{355} \text { or, } 360 x=5 \times 6000\)

or, \(x=\frac{5 \times 6000}{360}=\frac{250}{3}=83.3 \mathrm{~m}\)

∴ t = \(\frac{x}{5}=\frac{83.3}{5}=16.67 \mathrm{~s}\)

So, the man will listen to the echo after traveling 835 m, 16.67s after firing the gun.

Wave Motion And Its Types Class 11

Example 4. A gun is fired from an airplane moving horizontally with a velocity of 180 km h and the echo of the sound after reflection from the ground Is heard after 3s. What is the height of the airplane? The velocity of sound = 340 m · s^-1.
Solution:

Given

A gun is fired from an airplane moving horizontally with a velocity of 180 km h and the echo of the sound after reflection from the ground Is heard after 3s.

180 \(\mathrm{~km} \cdot \mathrm{h}^{-1}=\frac{180 \times 1000}{60 \times 60} \mathrm{~m} \cdot \mathrm{s}^{-1}=50 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Distance travelled by the plane in 3 s = AB = 50 x 3 m

So, \(A N=\frac{A B}{2}=\frac{50 \times 3}{2}=25 \times 3 \mathrm{~m}\)

Distance travelled by sound in that time = AO + OB =340 x3 m

i.e AO = \(\frac{340 \times 3}{2}=170 \times 3 \mathrm{~m}\)

So, height of the plane = ON = \(\sqrt{A O^2-A N^2}\)

= \(\sqrt{(170 \times 3)^2-(25 \times 3)^2}\)

= \(\sqrt{(510)^2-(75)^2} \approx 504.45 \mathrm{~m}\)

Numerical Problems On Echo Class 11 Physics

Example 5. A man standing 85 m away from a high wall is clapping in a regulated manner. When he claps twice per second, each clap coincides with the echo of its previous clap. Determining the velocity of sound in air.
Solution:

Given

A man standing 85 m away from a high wall is clapping in a regulated manner. When he claps twice per second, each clap coincides with the echo of its previous clap.

Time interval between two claps, t = \(\frac{1}{2}\) s

If V is the velocity of sound in air, 2s = Vt

∴ 2 x 85 = \(V \times \frac{1}{2} \quad \text { or, } V=85 \times 4=340 \mathrm{~m} \cdot \mathrm{s}^{-1} \text {. }\)

Example 6. A ship’s sound measuring experiment sends our pulses looking for echoes from submarines within a 3 km radius. What should be the pulse repetition frequency? Given, the velocity of sound in water = 1500 m · s^-1
Solution:

Given

A ship’s sound measuring experiment sends our pulses looking for echoes from submarines within a 3 km radius.

Total path travelled by the pulses = 3 + 3 = 6km = 6000m

Time taken by a pulse for the to and fro journey is,

t = \(\frac{6000}{1500}=4 \mathrm{~s}\)

∴ Pulse repetition frequency,

n = \(\frac{1}{4}\) per second = 15 per minute.

The pulse repetition frequency = 15 per minute.

Wave Motion Class 11 NCERT Solutions

Example 7. A man standing at a certain distance from a bill is heating a drum. He observes that if he beats the drum at the rate of 40 min^-1, the echo is not heard distinctly. He advances 90 m towards the hill and observes that If he beats the drum at the rate of 60 min^-1, the echo cannot be heard distinctly. Determine the distance of the first position of the man from the hill and aldo the velocity of sound.
Solution:

Given

A man standing at a certain distance from a bill is heating a drum. He observes that if he beats the drum at the rate of 40 min^-1, the echo is not heard distinctly. He advances 90 m towards the hill and observes that If he beats the drum at the rate of 60 min^-1, the echo cannot be heard distinctly.

Let the distance of the first position of the man from the hill be x and velocity of sound be V.

In the first case, the time interval between two consecutive sounds, \(t_1=\frac{60}{40}=\frac{3}{2} \mathrm{~s}\)

∴ When echo is just not heard distinctly, 2x = V x \(\frac{3}{2}\) s …(1)

In the second case, the time interval between two consecutive sounds, \(t_2=\frac{60}{60}\) = 1s

∴ In this case, when the echo is just not heard distinctly, 2(x-90) = V x 1 ……(2)

Dividing {2} by (1) we have, \(\frac{2(x-90)}{2 x}=\frac{V \times 2}{V \times 3} \quad \text { or, } 3 x-270=2 x \quad \text { or, } x=270 \mathrm{~m}\)

From equation (1) we have,

2 x 270 = \(V \times \frac{3}{2} \quad \text { or, } V=360 \mathrm{~m} \cdot \mathrm{s}^{-1} \text {. }\)

Wave Motion Velocity Of Sound In A Material Medium

The velocity with which sound waves will propagate in a material medium depends on two properties—density and elasticity—of the medium.

Definition Of Density In Physics: If the density of a medium is low, the effect of the pressure that a vibrating body exerts on such a medium can transmit through a large distance within a short time. On the other hand, if the density of the medium is high, the effect of pressure transmits through a comparatively small distance in equal time. Hence, the lengths of compression and rarefaction produced in a lighter medium become comparatively large and so the velocity of sound in this medium also becomes large.

Definition Of Elasticity: A vibrating particle exerts force on a medium. This results in elastic stress in the medium. Due to elastic stress, the compressed layer expands. The compressed layers of the medium which has large elasticity expand very rapidly and the expanded layers also contract very rapidly, i.e., the transformation of compression into rarefaction and vice versa takes a very short time. As a result, the velocity of sound in the medium increases.

From theoretical calculations Newton showed that the velocity of sound through a medium is given by, c = \(\sqrt{\frac{E}{\rho}}\)

where E = modulus of elasticity of the medium p = density of the medium

[As the symbol V will be used to represent volume in the next article, the velocity of sound is represented here by the symbol c.]

The velocity of sound in different media (at a given temperature)

Relation Between Torque And Angular Acceleration Class 11

Wave Motion Velocity Of Sound In A Gaseous Medium

Air or any gas is a material medium. So the formula of velocity of sound described in the previous section is applicable for a gas. Since gas has no length or size, the bulk modulus is the only modulus of elasticity for it. Hence, if ρ is the density of the gas, k is the bulk modulus, then the velocity of sound through the gas is given by,

c = \(\sqrt{\frac{k}{\rho}}\)…(1)

Newton’s Calculation: Sound wave propagates through a gaseous medium by the mechanism of formation of alternate layers of compression and rarefaction.

Newton assumed that propagation of sound through a gaseous medium is an isothermal process, i.e., successive compressions and rarefactions occur at such a rate that the temperature of the gaseous medium remains constant during the propagation though the pressure and volume of the gaseous medium may change.

Let the pressure and the volume of a particular amount of gas in a portion of the gaseous medium be p and V respectively.

During propagation of sound, suppose the pressure of this portion increases to p + p₁, and p₁ is very small with respect to p. As a result, its volume decreases to V- v, where v is very small with respect to V. So if the temperature remains constant, according to Boyle’s law we can write,

pV = \(\left(p+p_1\right)(V-v)=p V+p_1 V-p v-p_1 v\)

or, \(0=p_1 V-p v\)

[neglecting the term \(p_1 v\) which is very small]

or, \(\frac{p_1 V}{v}\)=p

or, \(p=\frac{p_1}{\frac{v}{V}}=\frac{\text { volume stress }}{\text { volume strain }}\)

So, bulk modulus, k = \(\frac{\text { volume stress }}{\text { volume strain }}\) = p

Proof By Calculus: According to Boyle’s law, pV = constant

On differentiation we have,

pdV + Vdp = 0 or p = \(\frac{-V d p}{d V}=-\frac{d p}{\frac{d V}{V}}\)

[the negative sign indicates that if pressure increases volume decreases]

∴ p = \(\frac{\text { volume stress }}{\text { volume strain }}\) = bulk modulus of the gas = k

So, from equation (1) we get,

Velocity of sound in a gaseous medium, c = \(\sqrt{\frac{p}{\rho}}\)…(2)

To understand how far this formula is correct, we can calculate the velocity of sound in air with this formula.

We know that standard atmospheric pressure = 76 cmHg = 76 x 13.6 x 980 dyn · cm^-2

and density of air at SIP = 0.001293 g · cm^-3

Therefore, the velocity of sound in air at STP according to Newton’s formula is

c = \(\sqrt{\frac{76 \times 13.6 \times 980}{0.001293}}=28000 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

= \(280 \mathrm{~m} \cdot \mathrm{s}^{-1} \text { (approx) }\)

However, it is found by different experiments that the velocity of sound in air at 0°C is 332 m · s^-1 (approx). From this, it can be concluded that there is a defect in Newton’s formula for determining the velocity of sound, in a gaseous medium.

Torque And Angular Acceleration Derivation Class 11

Laplace Correction Derivation: Scientist Laplace first pointed out that the propagation of sound waves through a gaseous medium takes place under adiabatic conditions and not under isothermal conditions as assumed by Newton.

According to Laplace’s assumption, compressions and rarefactions occur so quickly that the temperature of a gas cannot remain constant. On the other hand, the beat exchange does not take place among different portions of the gas during that small time interval.

As a result, the temperature of gaseous layers increases and decreases during the propagation of sound—the process is essentially adiabatic.

Now, the relation between pressure (p) and volume (V) of a. gas under adiabatic conditions is given by

pV^γ = constant

Here, \(\gamma=\frac{\text { molar specific heat of the gas at constant pressure }\left(C_p\right)}{\text { molar speciffic heat of the gas at constant volume }\left(C_v\right)}\)

Let the initial pressure and volume of a fixed amount of gas be p and V respectively. During the propagation of sound, pressure increases to p+p₁, whereas volume decreases to V-v. Here, p₁ is very small with respect to p and v is very small with respect to V.

So we write, \(p V^\gamma=\left(p+p_1\right)(V-\nu)^\gamma=\left(p+p_1\right) \cdot V^\gamma\left(1-\frac{\nu}{V}\right)^\gamma\)

or, p = \(\left(p+p_1\right)\left(1-\frac{\nu}{V}\right)^\gamma=\left(p+p_1\right)\left(1-\gamma \frac{\nu}{V}\right)\)

[neglecting other terms of binomial expansion]

= \(p+p_1-\frac{p \gamma \nu}{V}-\frac{p_1 \gamma \nu}{V}\)

or, \(p_1=\frac{\gamma p v}{V}\)….(1)

(neglecting the term \(\frac{p_1 \gamma \nu}{V} \text { as } p_1 \nu\) is very small)

∴ \(\gamma p=\frac{p_1}{\frac{v}{V}}\) = bulk modulus of the gas (k)

Hence, the bulk modulus of the gas, k = γp.

Torque And Angular Acceleration Formula Class 11

Proof By Calculus: The relation between pressure (p) and volume (V) of a gas under adiabatic condition is given by pV^ϒ = constant

On differentiation we have, \(V^\gamma d p+\gamma p^\gamma V^{\gamma-1} d V=0\)

or, \(d p+\frac{\gamma p d V}{V}=0\)

or, \(\gamma p=\frac{-d p}{\frac{d V}{V}}\)= bulk modulus of the gas (k)

So, from equation (1) we get, the velocity of sound in a gaseous medium, c = \(=\sqrt{\frac{\gamma p}{\rho}}\)….(2)

Using Laplace’s correction, the velocity of sound in air at STP,

c = \(\sqrt{\frac{1.4 \times 76 \times 13.6 \times 980}{0.001293}} \text { [for air, } \gamma=1.4 \text { ] }\)

= \(33117 \mathrm{~cm} \cdot \mathrm{s}^{-1}=331.2 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

This value of c Is very close to the experimental value of the velocity of sound in air. So we can come to the conclusion that Laplace’s equation for velocity of sound in a gaseous medium is correct.

Effect of Pressure, Temperature, Humidity, and Density of a Gas on the Velocity of Sound:

According to Laplace’s equation, if c is the velocity of sound in a gas of density ρ and pressure p, c = \(\sqrt{\frac{\gamma p}{\rho}}\)…(1)

Here γ is the ratio of the two molar-specific heats (at constant pressure and constant volume) of the gas. Now if 1 mol of gas is taken, mass = M, density \(\rho=\frac{M}{V}\)

and pV = RT (T = absolute temperature of the gas, R = universal gas constant)

So from equation (1) we get,

c = \(\sqrt{\frac{\gamma p}{\frac{M}{V}}}=\sqrt{\frac{\gamma p V}{M}}=\sqrt{\frac{\gamma R T}{M}}\)….. (2)

(Here, M = mass of 1 mol of gas, i.e., M is the molecular mass of the gas)

Effect Of Pressure: γ, R, and M are constants for a particular gas. So from equation (2) it is understood that, if the temperature of the gas remains constant, the velocity of sound does not change with a change in pressure, i.e., the pressure of the gas has no effect on the velocity of sound.

It can also be explained in a different way. At constant temperature, if the pressure of a gas is changed, the density of the gas also changes due to a change of the volume in such a way that the ratio \(\frac{p}{\rho}\) remains constant. So from equation (1) it can be said that the velocity of sound (c) remains constant with the change in pressure.

Torque And Angular Acceleration Notes Class 11

Effect Of Temperature: For a particular gas γ, R, and M—these three quantities are constants. So from equation (2) we get, c ∝ √T, i.e., the velocity of sound in the gas is directly proportional to the square root of its absolute temperature.

If c₁ and c₂ are the velocities of sound in the gas at absolute temperatures T₁ and T₂, then \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}\)

Let, \(T_1=0^{\circ} \mathrm{C}=273 \mathrm{~K}, T_2=t^{\circ} \mathrm{C}=(273+t) \mathrm{K}\)

If the velocities of sound at these two temperatures are \(c_0\) and c, then \(\frac{c_0}{c}=\sqrt{\frac{273}{273+t}}\)

or, \(c=c_0 \sqrt{\frac{273+t}{273}}=c_0\left(1+\frac{t}{273}\right)^{1 / 2} \approx c_0\left(1+\frac{1}{2} \cdot \frac{t}{273}\right)\)

= \(c_0(1+0.00183 t)\)

∴ c = \(c_0(1+0.00183 t)\)….(3)

The change of the velocity of sound due to any change in the temperature of the gas can be calculated with the help of equation (3).

Velocity of sound in air at 0°C, c₀ = 332 m · s^-1

So, c = 332(1 +0.00183t) = (332 + 0.61t) m · s^-1

Therefore, the velocity of sound in air increases by 0. 61 m · s^-1 or 61 cm · s^-1 for 1°C rise In temperature (61 cm · s^-1 ≈ 2ft · s^-1).

Effect Of Humidity: The density of water vapor is less (approximately 0.622 times) than the density of dry air at the same temperature and pressure. So if water vapor is mixed in the air, the density of air decreases. Hence, the velocity of sound in air increases, i.e., the velocity of sound in moist air is greater than that in dry air.

Let temperature of air = t°C; atmospheric pressure = p;

The velocity of sound in dry air at t°C = c;

The velocity of sound in moist air at t°C = c_m

Vapor pressure at that temperature = f

It can be shown from theoretical analysis that

c = \(c_m\left(1-0.378 \frac{f}{p}\right)^{1 / 2} \approx c_m\left(1-0.189 \frac{f}{p}\right)\)…(4)

Any experiment for determination of the velocity of sound is made in the normal atmosphere which is more or less humid. So, the velocity of sound determined by the experiment is the velocity of sound in moist air i.e., c_m. Thus tire velocity of sound in dry air, i.e., c can be obtained by using equation (4).

Relation Between Torque And Angular Momentum Class 11

Effect Of Density: Let two different gases be at the same temperature and pressure. Under this condition, if ρ₁ and ρ₂ are the densities of the two gases and c₁ and c₂ are the velocities of sound in the two gases,

⇒ \(c_1=\sqrt{\frac{\gamma p}{\rho_1}} ; c_2=\sqrt{\frac{\gamma p}{\rho_2}}\)

[It has been assumed that both the gases have the same γ]

So, \(\frac{c_1}{c_2}=\sqrt{\frac{\rho_2}{\rho_1}} \quad \text { i.e., } c \propto \frac{1}{\sqrt{\rho}}\)

Therefore, the velocity of sound in a gas is inversely proportional to the square root of its density.

For example, oxygen is 16 times, heavier than hydrogen. So velocity of sound in oxygen is \(\frac{1}{\sqrt{16}}\), i.e., \(\frac{1}{4}\) times the velocity of sound in hydrogen.

In the above discussion, γ of both gases has been taken to be equal. If each molecule of the two gases contains the same number of atoms, the values of γ for both are the same. Again if a different number of atoms are present in the molecules, corresponding values of γ are to be put in the formula.

Motion Velocity Of Sound In A Gaseous Medium Numerical Examples

Example 1. The velocity of sound in a gas at 51°C is 340 m · s^-1. What will be the velocity of sound if pressure is doubled and temperature becomes 127°C?
Solution:

Given

The velocity of sound in a gas at 51°C is 340 m · s^-1.

The pressure of the gas has no effect on the velocity of sound.

In this case velocity of sound will change only due to the change in temperature.

Initial temperature, T₁ = 51°C = (273 + 51) K = 324 K

Final temperature, T₂ = 127°C = (273 + 127) K = 400 K

We know that the velocity of sound in a gas is directly proportional to the square root of its temperature, i.e., c ∝√T.

∴ \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}\)

or, \(c_2=c_1 \sqrt{\frac{T_2}{T_1}}=340 \times \sqrt{\frac{400}{324}}\)

= \(340 \times \frac{20}{18}=378 \mathrm{~m} \cdot \mathrm{s}^{-1} \text { (approx.). }\)

Relation Between Moment Of Inertia And Torque Class 11

Example 2. The velocity of sound in a gas at 50°C is 340 m · s^-1. What will be the velocity of sound if pressure is doubled and temperature becomes 125°C?
Solution:

Given

The velocity of sound in a gas at 50°C is 340 m · s^-1.

The velocity of sound does not depend on the pressure of the gas.

Initial temperature, T₁ = 50°C = (50 + 273) K – 323 K

Final temperature, T₂ = 125°C = (125 + 273) K = 398 K

Now, velocity of sound, c ∝ √T,

i.e., \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}\)

or, \(c_2=c_1 \times \sqrt{\frac{T_2}{T_1}}=340 \times \sqrt{\frac{398}{323}}=377.4 \mathrm{~m} \cdot \mathrm{s}^{-1}\).

Example 3. Determine the velocity of sound in hydrogen at STP. At STP, density of the gas = 0.09 g L^-1; γ = 1.4
Solution:

Density, \(\rho=0.09 \mathrm{~g} \cdot \mathrm{L}^{-1}=\frac{0.09}{1000} \mathrm{~g} \cdot \mathrm{cm}^{-3}\)

= \(0.09 \times 10^{-3} \mathrm{~g} \cdot \mathrm{cm}^{-3}\)

Standard pressure, p = 76 x 13.6 x 980 dyn · cm^-2

Therefore, velocity of sound,

c = \(\sqrt{\frac{\gamma p}{\rho}} =\sqrt{\frac{1.4 \times 76 \times 13.6 \times 980}{0.09 \times 10^{-3}}}\)

= \(125525 \mathrm{~cm} \cdot \mathrm{s}^{-1}=1255.25 \mathrm{~m} \cdot \mathrm{s}^{-1} .\)

Torque And Angular Acceleration Numericals Class 11

Example 4. The ratio of γy of oxygen and methane is 21:20. The ratio of their densities at the same pressure is 2:1. lf the velocity of sound in oxygen is 316 m · s^-1, what is the velocity of sound in methane?
Solution:

Given

The ratio of γy of oxygen and methane is 21:20. The ratio of their densities at the same pressure is 2:1. lf the velocity of sound in oxygen is 316 m · s^-1,

If the velocities of sound in oxygen and methane are c₁ and c₂ respectively, then

⇒ \(c_1=\sqrt{\frac{\gamma_1 p}{\rho_1}}\) and \(c_2=\sqrt{\frac{\gamma_2 p}{\rho_2}}\)

∴\(\frac{c_1}{c_2}=\sqrt{\frac{\gamma_1}{\gamma_2} \times \frac{\rho_2}{\rho_1}}\)

or, \(c_2=c_1 \sqrt{\frac{\gamma_2}{\gamma_1} \times \frac{\rho_1}{\rho_2}}=316 \times \sqrt{\frac{20}{21} \times \frac{2}{1}} \approx 436 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Example 5. At what temperature the velocity of sound in nitrogen will be equal to its velocity in oxygen at 27°C?
Solution:

Since nitrogen and oxygen are both diatomic gases, the values of γ for both of them are equal.

The molecular mass of nitrogen, M₁ = 28

The molecular mass of oxygen, M₂ = 32

Velocity of sound, c = \(\sqrt{\frac{\gamma R T}{M}}\)

So, velocity of sound in nitrogen, \(c_1=\sqrt{\frac{\gamma R T_1}{M_1}}\)

velocity of sound in oxygen, c₂ = \(\sqrt{\frac{\gamma R T_2}{M_2}}\)

According to the question, c₁= c₂ and T₂ = 27°C = (273 + 27) K = 300 K

So, \(\sqrt{\frac{\gamma R T_1}{28}}=\sqrt{\frac{\gamma R \times 300}{32}}\)

or, \(T_1=\frac{300 \times 28}{32}=262.5 \mathrm{~K}=(262.5-273)^{\circ} \mathrm{C}\)

= \(-10.5^{\circ} \mathrm{C}\)

Torque And Angular Acceleration Examples Class 11

Example 6. The velocity of sound In hydrogen at 0tJC Is 1200 m · s^-1. If a certain amount of oxygen Is mixed with hydrogen, the velocity of sound decreases and becomes 500 m · s^-1, What Is the ratio of the volumes of hydrogen and oxygen In the mixture? It Is given that the density of oxygen Is 16 times that of hydrogen.
Solution:

Given

The velocity of sound In hydrogen at 0tJC Is 1200 m · s^-1. If a certain amount of oxygen Is mixed with hydrogen, the velocity of sound decreases and becomes 500 m · s^-1

We know, velocity of sound, c = \(\sqrt{\frac{\gamma p}{\rho}}\)

In case of hydrogen, 1200 = \(\sqrt{\frac{\gamma p}{\rho_1}}\)

In case of the given mixture, 500 = \(\sqrt{\frac{\gamma p}{\rho_2}}\)

∴ \(\frac{1200}{500}=\sqrt{\frac{\rho_2}{\rho_1}} \text { or, } \frac{\rho_2}{\rho_1}=\left(\frac{12}{5}\right)^2=\frac{144}{25}\)

Now if x volume of oxygen is mixed with 1 volume of hydrogen, the density of the mixture is given by,

⇒ \(\rho_2=\frac{1 \times \rho_1+x \times 16 \rho_1}{1+x}\)

or, \(\frac{\rho_2}{\rho_1}=\frac{1+16 x}{1+x}\)

∴\(\frac{1+16 x}{1+x}=\frac{144}{25}\)

or, \(25+400 x=144+144 x \quad \text { or, } 256 x=119\)

or, x = \(\frac{119}{256}\)

Hence, the ratio of the volumes of hydrogen and oxygen: 1 : (119/256) =256:119.

Example 7. What Is the velocity of sound in air saturated with water vapor at 27° C? It Is given that the velocity of sound in dry air at 0°C Is 332 m · s^-1 and aqueous tension at 27°C is 11.2 mmHg.
Solution:

The velocity of sound in dry air at 27°C,

c = 332(1 + 0.00183 x 27) = 332 x 1.05 m · s^-1

Aqueous tension at that temperature, f = 11.2 mm Hg = 1.12 cm Hg

If c_m is the velocity of sound in air saturated with water vapor at 27°C,

c = c_m(1-0.189 \({p}{f}\))= \(c_m\left(1-0.189 \times \frac{1.12}{76}\right)\)

= \(c_m \times 0.997\)

or, \(c_m=\frac{c}{0.997}=\frac{332 \times 1.05}{0.997}=350 \mathrm{~m} \cdot \mathrm{s}^{-1} (approx.).\)

Example 8. The velocity of sound In helium gas at -173°C is 582 m · s^-1, If the molecular mass of helium is 4, find the value of γ for the gas. (R = 8.31 x 10⁷ erg · mol^-1 · °C^-1)
Solution:

T = -173°C = (-173 + 273)K = 100K

The molecular mass of helium, M = 4

Velocity of sound, c = 582 m · s^-1 = 58200 cm · s^-1

Now, c = \(\sqrt{\frac{\gamma R T}{M}} \text { or, } \gamma=\frac{c^2 M}{R T}=\frac{(58200)^2 \times 4}{8.31 \times 10^7 \times 100}=1.63 \text {. }\)

Torque And Angular Acceleration Physics Class 11

Example 9. At STP, the velocity of sound in oxygen Is 317 m · s^-1. What is the velocity of sound In hydrogen at 30°C temperature and 374 mmHg pressure?
Solution:

At 0°C or 273 K, the velocity of sound in oxygen, c₁ =317 m · s^-1

Let c₂ be the velocity of sound in oxygen at 30°C or 303 K.

Now, \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}} \quad \text { or, } c_2=c_1 \times \sqrt{\frac{T_2}{T_1}}\)

Again at the same temperature, the velocity of sound in two gases is inversely proportional to the square root of their densities. So, if c₂‘ is the velocity of sound in hydrogen at 30°C,

∴ \(\frac{c_2{ }^{\prime}}{c_2}=\sqrt{\frac{\rho}{\rho^{\prime}}} \text { or, } c_2{ }^{\prime}=c_2 \times \sqrt{\frac{\rho}{\rho^{\prime}}}\)

∴ \(c_2{ }^{\prime}=317 \times \sqrt{\frac{303}{273}} \times \sqrt{\frac{16}{1}}=1336 \mathrm{~m} \cdot \mathrm{s}^{-1} \text { (approx.) }\)

The velocity of sound does not depend on the pressure of the gas. So, this velocity will remain the same at 374 mmHg pressure.

Example 10. The masses of 1L of hydrogen and 1L of air are 0.0896 g and 1.293 g respectively at the same temperature and pressure. If the velocity of sound In air at that temperature Is 330 m · s^-1, what will be the corresponding velocity In hydrogen?
Solution:

Given

The masses of 1L of hydrogen and 1L of air are 0.0896 g and 1.293 g respectively at the same temperature and pressure. If the velocity of sound In air at that temperature Is 330 m · s^-1

We know, the velocity of sound in a gas, c = \(\sqrt{\frac{\gamma p}{\rho}} .\)

γ = 1.41 for both hydrogen and air. If the velocities of sound in hydrogen and air at the same temperature and pressure are c_H and c_air respectively,

⇒ \(\frac{c_{\mathrm{H}}}{c_{\text {air }}}=\sqrt{\frac{\rho_{\text {air }}}{\rho_{\mathrm{H}}}}\)

or, \(c_{\mathrm{H}}=c_{\text {air }} \times \sqrt{\frac{\rho_{\text {air }}}{\rho_{\mathrm{H}}}}=330 \times \sqrt{\frac{1.293}{0.0896}}=1253.6 \mathrm{~m} \cdot \mathrm{s}^{-1} .\)

Wave Motion Short Answer Type Questions

Question 1. The equation y= a(sinkxcosωt- coskxsinωt) represents

1. A progressive wave propagating along the positive x-axis with velocity ω/k
2. A progressive wave propagating along the negative x-axis with velocity ω/k
3. A stationary wave
4. Not a wave motion

Answer:

Here, y = asin(kx-ωt); a progressive wave of ω/k velocity, along +ve x direction.

The option 1 is correct.

Question 2. The wavelength of a traveling wave is 2 m. What is the phase difference between two particles 1 m apart in the path of the wave?
Answer:

Given

The wavelength of a traveling wave is 2 m.

For λ = 2m, the phase changes by 2π.

So, for two points separated by 1 m, phase difference = \(\frac{\pi}{2}\) = π

Wave Motion Class 11 Physics Notes

Question 3. Are sound waves longitudinal or transverse?
Answer:

Sound waves are longitudinal waves.

Question 4. The equation of a traveling wave is y- 20 sin (0.2πx-50πt), where x and y are in cm and t is in second. Find out the

1. Amplitude,
2. Wavelength,
3. Frequency and
4. Velocity of the wave.

Answer:

Equation of progressive wave, y = 20 sin (0.2πx-50πt)

1. Amplitude (a) = 20 cm

2. Here, k = \(0.2 \pi \quad \text { or, } \frac{2 \pi}{\lambda}=0.2 \pi\)

∴ \(\lambda=\frac{2 \pi}{0.2 \pi}=10 \mathrm{~cm}\)

So, wavelength = 10 cm

3. According to given equation, angular velocity (ω) = 50 π;

∴ n = \(\frac{\omega}{2 \pi}=\frac{50 \pi}{2 \pi}=25\)

So, frequency = 25 Hz

4. Velocity (V) =nλ = 25 x 10 = 250 cm · s^-1

Types Of Wave Motion Class 11

Question 5. The percentage change of velocity of sound when temperature increases from 0°C to 20°C is

1. 1.5%
2. 2.5%
3. 1.75%
4. 2%

Answer:

The velocity of sound, c ∝ √T

Here, T₁ = 0 + 273 = 273 K

T₂ = 20 + 273 = 293 K

∴ \(\frac{c_{20}}{c_0}=\sqrt{\frac{293}{273}}=\left(1+\frac{20}{273}\right)^{1 / 2} \approx 1+\frac{1}{2} \cdot \frac{20}{273}=\frac{283}{273}\)

So, percentage change of velocity

= \(\left(\frac{283}{273}-1\right) \times 100=3.66 \%\)

None of the options is correct.

Numerical Problems On Wave Motion Class 11

Question 6. The velocity of sound in oxygen gas at STP is v. What will be the velocity of sound in Helium gas under the same conditions?
Answer:

Given

The velocity of sound in oxygen gas at STP is v.

Velocity of sound, c = \(\sqrt{\frac{\nu R T}{M}}\)

At STP, the molar mass of oxygen, M = 32 g

The molar mass of helium, M’ = 4g

Now as oxygen is a diatomic gas, v = \(\frac{7}{5}\)

Again helium is a monoatomic gas, v’ = \(\frac{5}{3}\)

So, \(\frac{\nu^{\prime}}{\nu}=\sqrt{\frac{\nu^{\prime}}{\nu}} \cdot \sqrt{\frac{M}{M^{\prime}}}=\sqrt{\frac{5}{\frac{5}{5}} \times \frac{32}{4}}=\sqrt{\frac{25}{21} \times 8}=3.086\)

∴ v’ = 3.086 v

Question 7. Two sound waves having a phase difference of 60° have path difference of

1. \(2 \lambda\)
2. \(\frac{\lambda}{6}\)
3. \(\frac{\lambda}{2}\)
4. \(\frac{\lambda}{3}\)

Answer:

Phase difference, \(\phi=\frac{2 \pi}{\lambda}\) x path difference (Δx)

or, \(60^{\circ}=\frac{\pi}{3}=\frac{2 \pi}{\lambda} \Delta x\)

∴ \(\Delta x=\frac{\lambda}{6}\)

The option B is correct.

Wave Motion Class 11 NCERT Solutions

Question 8. A stone is dropped from the top of a well of depth 39.2 m and a sound is heard when it reaches the bottom surface after a time of 2.95 s. Find the velocity of sound in the air. (g = 9.8 m/s²)
Answer:

Given

A stone is dropped from the top of a well of depth 39.2 m and a sound is heard when it reaches the bottom surface after a time of 2.95 s.

Depth of the well, h = 39.2 m

The time taken by the stone to travel a 39.2 m distance is,

t = \(\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 39.2}{9.8}}=2 . \sqrt{2}=2.83 \mathrm{~s}\)

The time taken for sound to travel h distance is, t’ = (2.95 – 2.83) = 0.12 s

∴ The velocity of sound in air, v = \(\frac{h}{t^{\prime}}=\frac{39.2}{0.12}\) = 326.67 m/s

Question 9. The frequency of a particle vibrating In a medium is fHz. How many waves are generated in 5 seconds in the medium?
Answer:

Given

The frequency of a particle vibrating In a medium is fHz.

The number of waves generated in 1 second = f

∴ The number of waves generated in 5 seconds = 5f

Wave Motion Examples Class 11

Question 10. A tuning fork in air vibrates at 30 Hz with 5 cm amplitude. If the velocity of sound in air is 330 m · s^-1, derive the expression for the generated traveling wave.
Answer:

Given

A tuning fork in air vibrates at 30 Hz with 5 cm amplitude. If the velocity of sound in air is 330 m · s^-1,

Amplitude, A = 5 cm = 0.05 m; frequency n = 30 Hz;

velocity, V = 330 m · s^-1

∴ Wavelength, \(\lambda=\frac{V}{n}=\frac{330}{30}=11 \mathrm{~m}\)

The expression for the generated traveling wave,

y = \(A \sin \frac{2 \pi}{\lambda}(V t-x)=0.05 \sin \frac{2 \pi}{11}(330 t-x) \mathrm{m}\)

Question 11. The path difference of two particles on a wave corresponding to a phase difference of 60° is

1. \(2 \lambda\)
2. \(\frac{\lambda}{2}\)
3. \(\frac{\lambda}{6}\)
4. \(\frac{\lambda}{3}\)

Answer:

The option 3 is correct.

Question 12. When sound enters water from air or vice-versa, which physical quantity of the waves remains unchanged?
Answer:

When sound enters water from air or vice-versa, the frequency of the waves remains unchanged.

Question 13. Two tuning forks vibrating simultaneously produce 5 beats per second. The frequency of one fork is 275 Hz. A small wax is attached to the other fork and 2 beats per second are produced when the two vibrate simultaneously. Find the frequency of the other fork.
Answer:

Given

Two tuning forks vibrating simultaneously produce 5 beats per second. The frequency of one fork is 275 Hz. A small wax is attached to the other fork and 2 beats per second are produced when the two vibrate simultaneously.

Let the frequency of the other fork be x.

Beat frequency = difference in the frequencies of the two tuning forks.

If x< 275 Hz, before waxing we have, 275 – x = 5 H or x = 270 Hz. After waxing, x will decrease, so the beat frequency will increase.

∴ x > 275 Hz and before waxing we have, x – 270 = 5

or x = 280 Hz. After waxing, A will decrease slightly, so the beat frequency will decrease to 2.

Progressive And Stationary Waves Class 11

Question 14. The velocity of sound in air at 20°C and 1 atm pressure is 344.2 m/s. At 40°C and 2 atm pressure, the velocity of sound in air is approximately

1. 350 m/s
2. 350 m/s
3. 303 m/s
4. 370 m/s

Answer:

If the velocities of sound are c₁ and c₂ at absolute temperatures T₁ and T₂, respectively, then

∴ \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}\)

Here, T₁ = 273 + 20 = 293 K and, T₂ = 273 + 40 = 313 K

∴ \(c_2=c_1 \times \sqrt{\frac{T_2}{T_1}}=344.2 \times \sqrt{\frac{313}{293}}\)

= 355.75 ≈ 356 m/s

The option 2 is correct.

Question 15. If the pressure, temperature, and density of an ideal gas are denoted by p, T, and ρ respectively, the velocity of sound in the gas is

1. Proportional to √p, when T is constant
2. Proportional to √T
3. Proportional to √p, when ρ is constant
4. Proportional to T

Answer:

Velocity of sound in air, \(\nu=\sqrt{\frac{\delta p}{\rho}}\)…(1)

or, \(\nu=\sqrt{\frac{\delta R T}{M}}\)…(2)

⇒ \(\left[because p V=R T \text { or, } p=\frac{R T}{V}=\frac{R T}{\frac{M}{\rho}}\right]\)

According to equation (1), v ∝ √p when ρ is constant.

According to equation (2), v ∝ √T

The options 2 and 3 are correct.

Transverse And Longitudinal Waves Class 11

Question 16. A uniform string of length 20 m is suspended from a rigid support. A short wave pulse is introduced at its lowest end. It starts moving up the string. The time taken to reach the support is

1. 2π√2 s
2. 2s
3. 2√2 s
4. √2s

Answer:

Tension at height y from the lowest end of the string, T = \(\frac{Mgy}{L}\)

[M is the mass of the string, L is the length of the string]

∴ The velocity of the wave at the height y of the string, \(\frac{d y}{d t}=\nu=\sqrt{\frac{T}{\mu}}\) [μ = mass per unit length of the string]

= \(\sqrt{\frac{\frac{M g y}{L}}{\frac{M}{L}}}=\sqrt{g y}\)

∴ \(\frac{d y}{\sqrt{y}}=\sqrt{g} d t\)

or, \(\int_0^L \frac{d y}{\sqrt{y}}=\sqrt{g} \int_0^t d t\)

or, \(\left.2 \sqrt{y}\right|_0 ^L=\left.\sqrt{g} t\right|_0 ^t\)

or, \(2 \sqrt{L}=\sqrt{g} t\)

∴ t = \(2 \sqrt{\frac{L}{g}}=2 \sqrt{\frac{20}{10}}=2 \sqrt{2} \mathrm{~s}\)

The option 3 is correct.

Characteristics Of Wave Motion Class 11

Question 17. A uniform rope of length L and mass m₁ hangs vertically from a rigid support. A block of mass m₂ is attached to the free end of the rope. A transverse pulse of wavelength λ₁ is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ₂. The ratio λ₂/λ₁ is

1. \(\sqrt{\frac{m_1+m_2}{m_2}}\)
2. \(\sqrt{\frac{m_2}{m_1}}\)
3. \(\sqrt{\frac{m_1+m_2}{m_1}}\)
4. \(\sqrt{\frac{m_1}{m_2}}\)

Answer:

Tension at the lower end of the rope, T₁ = m₂g

Tension at the top of the rope, T₂ = (m₁ + m₂)g

The velocity of the transverse wave, \(\nu=n \lambda=\sqrt{\frac{T}{\mu}}\)

[where n = frequency, λ = wavelength and μ = mass per unit length of the rope]

Hence, λ ∝ √T

∴ \(\frac{\lambda_1}{\lambda_2}=\sqrt{\frac{T_1}{T_2}}=\sqrt{\frac{m_2 g}{\left(m_1+m_2\right) g}}\)

= \(\sqrt{\frac{m_2}{m_1+m_2}}\)

or, \(\frac{\lambda_2}{\lambda_1}=\sqrt{\frac{m_1+m_2}{m_2}}\)

The option 1 is correct.

Wave Motion Formula Class 11

Question 18. A metal rod of 1 m in length, is dropped exactly vertically onto a hard metal floor. With an oscilloscope, it is determined that the impact produces a longitudinal wave of 1.2 kHz frequency. The speed of sound in the metal rod is

1. 600 m/s
2. 2400 m/s
3. 1800 m/s
4. 1200 m/s

Answer:

For the fundamental wave in the rod of length l, l \(=\frac{\lambda}{2}\)

Hence, Aλ =2l [l = wavelength]

∴ Velocity of sound,

V= nλ = (1.2 x 10³) x 2 x 1 = 2400 m/s

The option 2 is correct.

Question 19. The transverse harmonic wave on a string is described by Y(x,t) = 3.0sin(36t + 0.018x + π/4) where x and y are in cm and t is in second, The positive direction of x is from left to right,

1. Is this a traveling wave or a stationary wave? Give its direction of propagation.
2. What are its amplitude and frequency?
3. What is the initial phase at the origin?
4. What is the least distance between two successive crests in the wave?

Answer:

Compared with the general equation of a traveling wave,

y = a sin(ω- kx+ θ), we get, a = 3.0 cm,

ω = 36 Hz, k = -0.018 cm^-1 and \(\theta=\frac{\pi}{4}\)

1. The given equation corresponds to a traveling wave. As k is negative, the wave propagates along the negative x-direction.

2. Amplitude, a = 3.0 cm; frequency, \(\nu=\frac{\omega}{2 \pi}=\frac{36}{2 \times 3.14}=5.73 \mathrm{~Hz} .\)

3. Putting x = 0 and t = 0, we get

y = a sinθ = a sin \(\frac{\pi}{4}\)

So the initial phase at the origin = \(\frac{\pi}{4}\)

4. In magnitude, k = 0.018 cm^-1.

As k =\(\frac{2\pi}{\lambda}\), the wavelength,

∴ \(\frac{2\pi}{k}\) = 349 cm = least distance between two successive crests

Wave Motion Class 11 Important Questions

Question 20. What change is observed when a wave gets reflected from a hard and rigid support?
Answer:

• The reflected wave would propagate in the reverse direction, and
• Its phase would be reversed, i.e. a 180° phase difference would be introduced between the incident and the reflected waves.

Question 21. Though a violin note and a si tar note may have the same frequency, yet we can distinguish between the two notes. Explain how?
Answer:

• A violin note and a sitar note may have the same frequency or the same combination of frequencies. They may also have the same loudness.
• Yet, we can always distinguish between them because of a third property, which is essentially different for the two notes.
• This is the property called quality or timbre. The difference in timbre arises due to the distinct shapes of the waveforms associated with different musical notes.

Wave Motion Derivation Class 11 Physics

Question 22. If y = sin(3.6t + 0.018 x π/4) cm, find the amplitude and velocity of the wave.
Answer:

Given

y = sin(3.6t + 0.018 x π/4) cm

Comparing with the general equation y = asin(ωt -kx+θ) of a progressive wave, we get,

Amplitude, a = 3 cm,

Angular frequency, ω = 2πn = 3.6 Hz

and wave number, k = \(\frac{2 \pi}{\lambda}\) = -0.018 cm^-1

(The negative value means wave propagation in the negative x direction).

The velocity of the wave,

∴ V = \(n \lambda=\frac{2 \pi n}{\frac{2 \pi}{\lambda}}=\frac{\omega}{k}=\frac{3.6}{0.018}=200 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

Kinetic Theory Of Gases

Question 1. Which one of the following is not true for an ideal gas?

1. The molecules of an ideal gas move randomly
2. The molecules of an ideal gas attract one another
3. The volume of the molecules of an ideal gas is negligible
4. The pressure of an ideal gas increases with an increase in the velocity of its molecules

Answer: 2. The molecules of an ideal gas attract one another is correct

Question 2. A monatomic ideal gas is heated at constant pressure. How much fraction of heat is used to increase internal energy?

1. 2/5
2. 3/5
3. 3/7
4. 3/4

Answer:

If ΔT is the increase in temperature of a monoatomic ideal gas, increase in internal energy, \(\Delta E=\frac{3}{2} R \Delta T\) [for 1 mol gas]

Again, molar specific heat at constant pressure, \(C_p=\frac{5}{2} R\).

So, given heat to increase the temperature by ΔT at constant pressure = \(C_p \Delta T=\frac{5}{2} R \Delta T\)

Hence, the required fraction

= \(\frac{\text { increase in internal energy }}{\text { given heat }}=\frac{\frac{3}{2} R \Delta T}{\frac{5}{2} R \Delta T}=\frac{3}{5}\)

The option 2 is correct.

Kinetic Theory Of Gases Class 11 Notes

Question 3. Kinetic theory proves that, the pressure of a gas p = \(\frac{2 E}{3 v}\)(where v = 1 molar volume, E = kinetic = energy).
Answer:

Given

The pressure of a gas p = \(\frac{2 E}{3 v}\)(where v = 1 molar volume, E = kinetic = energy)

Molar mass of the gas = M;

Number of molecules = Avogadro’s number = N;

Molar volume of the gas = v = \(\frac{M}{\rho} \text {. }\)

We know, pressure, \(p=\frac{1}{3} \rho c^2\)

Here, ρ = density of the gas,

c = rms speed of gas molecules

Now, the kinetic energy of the gas molecules,

E = \(\frac{1}{2} m c_1^2+\frac{1}{2} m c_2^2+\cdots+\frac{1}{2} m c_N^2\)

= \(\frac{1}{2} m N \frac{c_1^2+c_2^2+\cdots+c_N^2}{N}\)

= \(\frac{1}{2} M c^2=\frac{1}{2} M \cdot \frac{3 p}{\rho}=\frac{3}{2} p v\)

Hence, \(p=\frac{2 E}{3 v}\)

Kinetic Theory Of Gases Class 11 Numericals

Question 4. In thermal equilibrium, the rms velocity of a gas molecule is

1. Proportional to T²
2. Proportional to T²
3. Proportional to √T
4. Zero

Answer:

rms speed of gas molecule, = \(\sqrt{\frac{3 R T}{M}}\)

The option 3 is corrections

Question 5. Write the expression for mean free path
Answer:

The expression for mean free path

Mean free path, \(\lambda=\frac{1}{\pi \sigma^2 n}\)

where n = number of molecules in unit volume;

= diameter of each gas molecule.

Question 6. From fonetic theory of gases proves that the pressure of 1 a gas p = 2E/3V, where V = 1 molar volume, E = Kinetic energy.
Answer:

Given

Molar mass of the gas =M, Number of molecules = Avogadro number = N,

Molar volume = V = \(\frac{M}{\rho}\), pressure = p = \(\frac{1}{3} \rho c^2\), here = density of gas, c= rms speed.

Kinetic energy of gas molecules, E

= \(\frac{1}{2} m c_1^2+\frac{1}{2} m c_2^2+\cdots+\frac{1}{2} m c_N^2\)

= \(\frac{1}{2} m N \frac{c_1^2+c_2^2+\cdots+c_N^2}{N}=\frac{1}{2} M c^2=\frac{1}{2} M \cdot \frac{3 p}{c}=\frac{3}{2} p V\)

Therefore, \(p=\frac{2 E}{3 V}\)

Question 7. The volume and pressure of two moles of an ideal gas are V and p respectively Another 1 mol ideal gas haring volume 2V also exerts the same pressure p. Molecular mass of the second gas is 16 times that of the first gas. Compare the rms velocities of the two gases.
Answer:

Given

The volume and pressure of two moles of an ideal gas are V and p respectively Another 1 mol ideal gas haring volume 2V also exerts the same pressure p. Molecular mass of the second gas is 16 times that of the first gas.

If the temperature of the first gas is \(T_1\), then \(p V=2 R T_1\) and the temperature of the second gas \(T_2\), then P.

then \(P \cdot 2 \mathrm{~V}=R T_2 or, p \mathrm{~V}=\frac{1}{2} R T_2\)

According to the question, \(2 R T_1=\frac{1}{2} R T_2 \quad \text { or } \frac{T_1}{T_2}=\frac{1}{4} \)

rms speed, c = \(\sqrt{\frac{3 R T}{M}}\)

∴ \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2} \cdot \frac{M_2}{M_1}}=\sqrt{\frac{1}{4} \times \frac{16}{1}}=\frac{2}{1}\)

or, \(c_1=2 c_2\)

Kinetic Theory Of Gases Class 11 Important Questions

Question 8. The perfect equation for 4g ofhydroÿst gas is

1. pV = RT
2. pV = 2RT
3. pV = 1/2 RT
4. pV = 4RT

Answer:

The number of moles in 4 g of hydrogen gas.

n = \(\frac{m}{M}=\frac{4}{2}=2 \mathrm{~mol}\)

∴ perfect equation, pV = nRT

on pV=2RT

The option 2 is correct.

Question 9. The relation \(p=\frac{1}{3} m n c_{m s}^2\), shows that the mean kinetic energy of a molecule is the same for all types of gases.
Answer:

Given, \(p=\frac{1}{3} m n c_{\text {rms }}^2=\frac{1}{3} \frac{m N}{V} c_{\text {rms }}^2\)

[N= number of molecules, V= volume]

or, \(\frac{1}{3} m c_{\mathrm{mms}}^2=\frac{p V}{N}=\frac{\left(\frac{N}{N_n}\right) R T}{N}\)

(\(N_A\)= Avogadro’s number)

or \(\frac{1}{2} m c_{\mathrm{rms}}^2=\frac{3 R T}{2} \frac{R}{N_A}\)

∴ mean kinetic energy of a molecule = \(\frac{1}{2} m c_{\text {rms }}^2=\frac{3 R T}{2} \frac{R T}{N_A}\)

Is the same for all types of gases at a particular temperature.

Kinetic Theory Of Gases Class 11 Derivations

Question 10. The rms speed of oxygen is v at a particular temperature. If the temperature is doubled and oxygen molecules dissociate Into oxygen atoms, the rms speed becomes

1. v
2. √2v
3. 2v
4. 4v

Answer:

The rms speed of oxygen molecule, v = \(\sqrt{\frac{2 R T}{M}}\)

When the molecules dissociate into oxygen atoms, molar mass will change from M to M/2 (when the temperature changes from T to 2 T)

Then, rms speed = \(\sqrt{\frac{3 R \cdot 2 T}{M / 2}}=2 \sqrt{\frac{3 R T}{M}}=2 v\)

The option 3 is correct.

Question 11. If the rms velocity of hydrogen gas at a certain temperature is c, then the rms velocity of oxygen gas at the same temperature is

1. \(\frac{c}{8}\)
2. \(\frac{c}{10}\)
3. \(\frac{c}{4}\)
4. \(\frac{c}{2}\)

Answer:

rms velocity of hydrogen gas, c = \(\sqrt{\frac{3 R T}{2}}\)

rms velocity of oxygen gas, \(c_{\mathrm{O}_2}=\sqrt{\frac{3 R T}{32}}\)

∴ \(c_{\mathrm{O}_2}=\sqrt{\frac{2}{32}} \times c=\frac{c}{4}\)

The option 3 is correct.

Question 12. The temperature of an ideal gas, initially at 27°C, is raised by 6°C. The rms velocity of the gas molecule will,

1. Increase by nearly 2%
2. Decrease by nearly 2%
3. Increase by nearly 1%
4. Decrease by nearly 1%

Answer:

⇒\(\nu_{\mathrm{rms}} \propto \sqrt{T}\)

or, \(\frac{\Delta \nu}{\nu}=\frac{1}{2} \frac{\Delta T}{T}=\frac{1}{2} \times \frac{6}{(273+27)}=\frac{1}{100}=1 \%\)

The option 3 is correct

Question 13. An open pipe made up of glass is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by an additional 46 cm. What will be the length of the air column above the mercury in the tube now? (atm pressure = 76 cm of Hg)

1. 16 cm
2. 22 cm
3. 38 cm
4. 6 cm

Answer:

Let <α = cross-sectional area of the pipe (in cm²)

So, initially, the volume of air above mercury, V₁ = 8α cm³; pressure, p₁ = 76 cm Hg.

When the top of the pipe is (46 + 8) or 54 cm higher than the outer mercury level, let x = rise of mercury level inside the pipe.

Then, the volume of air inside the pipe, v₂ = (54 – x)a cm³

and its pressure, p₂ = (76 – x) cm Hg

From Boyle law, p₁V₁ = p₂V₂

or, 76 x 8a = (76 – x)(54 – x)a

or, 608 = 4104- 130x+ x²

or, x² – 130x + 3496 = 0

or, (x-38)(x-92) = 0;

So, x = 38 cm or, x = 92 cm

The only physically meaningful solution is x = 38 cm Therefore, the length of the air column in the pipe above mercury =54-38 = 16 cm

The option 1 is correct.

Question 14. Consider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion, the average time of collision between molecules increases as V^q, where V is the volume of the gas. The value of q is  \(\left(\gamma=\frac{C_p}{C_\nu}\right)\)

1. \(\frac{3 \gamma+5}{6}\)
2. \(\frac{3 \gamma-5}{6}\)
3. \(\frac{\gamma+1}{2}\)
4. \(\frac{\gamma-1}{2}\)

Answer:

The rms speed of the molecules, c = \(\sqrt{3 R T / M}\)

Mean free path, \(\lambda=\frac{1}{\sigma^2 n}=\frac{1}{\sigma^2 \frac{N}{\nu}}\)

[N = number of molecules, cr = diameter of the molecules]

Average time of collision between the molecules,

t = \(\frac{\lambda}{c}=\frac{V}{\sigma^2 N} \frac{1}{\sqrt{3 R T / M}}\)

or, \(t \propto \frac{V}{\sqrt{T}}\)

or, \(T \propto \frac{V^2}{t^2}\)

Again, in the adiabatic process, \(T V^{\gamma-1}=\text { constant } \quad \text { or, } T \propto V^{1-\gamma}\)

∴ \(\frac{V^2}{t^2} \propto V^{1-r}\)

or, \(t^2 \propto v^{\gamma+1}\) or, \(t \propto V^{\frac{\gamma+1}{2}}\)

Hence, \(q=\frac{\gamma+1}{2}\)

The option 3 is correct

Kinetic Theory Of Gases Formula Class 11

Question 15. An ideal gas undergoes a quasistatic, reversible process in which its molar heat capacity C remains constant. If during this process the relation of pressure p and volume V is given by pVⁿ = constant, then n is given by (here C_p and C_v are molar specific heat at constant pressure and constant volume, respectively)

1. n = \(\frac{C_p}{C_\nu}\)
2. n = \(\frac{C-C_p}{C-C_\nu}\)
3. n = \(\frac{C_p-C}{C-C_\nu}\)
4. n = \(\frac{C-C_\nu}{C-C_p}\)

Answer:

Here, \(p V^n=k\) (constant)….(1)

For \(1 \mathrm{~mol}\) of ideal gas,

pV = RT…(2)

Dividing (1) by (2) we get, \(V^{n-1} T=\frac{k}{R}\)

∴ \(\left(\frac{d V}{d T}\right)=\frac{V}{(n-1) T}=\frac{V}{(1-n) T}\)

According to first law of thermodynamics,

dQ = \(C_\nu d T+p d V\)

∴ \(\frac{d Q}{d T}=C_\nu+p\left(\frac{d V}{d T}\right)=C_\nu+\frac{p V}{(1-n) T}=C_\nu+\frac{R}{1-n}\)

Hence, thermal capacity, \(C=C_\nu+\frac{R}{1-n}\)

or, \(1-n=\frac{R}{C-C_v}\)

or, \(n=1-\frac{R}{C-C_\nu}=\frac{C-\left(C_\nu+R\right)}{C-C_\nu}=\frac{C-C_p}{C-C_\nu}\)

(because \(C_p-C_v=R\))

The option 2 is correct.

Question 16. The mean free path of a molecule of gas (radius r) is inversely proportional to

1. r³
2. r²
3. r
4. √r

Answer:

Mean free path,

λ = \(\frac{1}{\sqrt{2} \pi d^2 n}=\frac{1 \times 4}{\sqrt{2} \pi r^2 n}\)

∴ \(\lambda \propto \frac{1}{r^2}\)

The option 2 is correct

Question 17. The ratio of the specific heats \(\frac{C_p}{C_v}=\gamma\) in terms of degrees of freedom (n) is given by

1. \(\left(1+\frac{1}{n}\right)\)
2. \(\left(1+\frac{n}{3}\right)\)
3. \(\left(1+\frac{2}{n}\right)\)
4. \(\left(1+\frac{n}{2}\right)\)

Answer:

⇒ \(C_\nu=\frac{n}{2} R, C_P=\frac{n}{2} R+R=\frac{n+2}{2} R\)

∴ \(\gamma=\frac{\frac{n+2}{2} R}{\frac{n}{2} R}=\frac{n+2}{n}=1+\frac{2}{n}\)

The option 3 is correct.

Question 18. The molecules of a given mass of a gas have rms velocity of 200 m · s^-1 at 27 °C and 1.0 x 10⁵ N · m^-2 pressure. When the temperature and pressure of the gas are respectively, 127 °C and 0.05 x 10⁵ N · m^-2, the rms velocity of its molecules in m · s^-1 is

1. \(\frac{400}{\sqrt{3}}\)
2. \(\frac{100 \sqrt{2}}{3}\)
3. \(\frac{100}{3}\)
4. \(100 \sqrt{2}\)

Answer:

rms speed of gas molecule, c ∝ √T

∴ \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}=\sqrt{\frac{27+273}{127+273}}=\sqrt{\frac{300}{400}}=\frac{\sqrt{3}}{2}\)

or, \(c_2=\frac{2}{\sqrt{3}} c_1=\frac{2}{\sqrt{3}} \times 200=\frac{400}{\sqrt{3}} \mathrm{~m} / \mathrm{s}\)

The option 1 is correct.

Kinetic Theory Of Gases Assumptions Class 11

Question 19. When the temperature of a gas is raised from 30°C to 90°C, the percentage Increase in the rms velocity of the molecules will be

1. 60%
2. 10%
3. 15%
4. 30%

Answer:

30°C = 303K, 90°C = 363K

rms speed, \(c \propto \sqrt{T}\)

Hence, \(\frac{c_2}{c_1}=\sqrt{\frac{T_2}{T_1}}=\sqrt{\frac{363}{303}}=\sqrt{1.2} \approx 1.1\)

∴ The percentage increase

= \(\frac{c_2-c_1}{c_1} \times 100=\left(\frac{c_2}{c_1}-1\right) \times 100\)

= \((1.1-1) \times 100=10 \%\)

The option 2 is correct.

Question 20. At what temperature will the rms speed of oxygen molecules become just sufficient for escaping from the earth’s atmosphere? [Given: Mass of oxygen molecule (m) = 2.76 x 10^-26 kg Boltzmann’s constant k =
1.38 x 10^-23 J • K^-1]

1. 5.016 X10⁴ K
2. 8.360 x 10⁴ K
3. 2.508 x 10⁴K
4. 1.254 x 10⁴ K

Answer:

Escape velocity of a body for the earth, \(v_e=\sqrt{2 g R}=\sqrt{2 \times 9.8 \times 6400 \times 10^3}\)

= 11200 m/s

Let us consider, at temperature TK, the escape velocity of the oxygen molecules will be (v_e).

Then, \(\sqrt{\frac{3 k_B T}{m}}=v_e\)

or, \(\frac{3 \times 1.38 \times 10^{-23}}{2.76 \times 10^{-26}} \cdot T=(11200)^2\)

or, T = \(8.363 \times 10^4 \mathrm{~K}\)

The option 2 is correct.

Question 21. What would be the effect on the rms speed of gas molecules if the temperature of the gas is increased by a factor of 4?
Answer:

We know, rms speed, c = \(\sqrt{\frac{3 R T}{M}}\)

∴ \(c \propto \sqrt{T}\)

Now, \(\frac{c_1}{c_2}=\sqrt{\frac{T_1}{T_2}}=\sqrt{\frac{T_1}{4 T_1}}=\frac{1}{2}\)

(since \(T_2=4 T_1\))

or, \(\quad c_2=2 c_1\)

So, rms speed is doubled

Question 22. A flask contains Argon and Chlorine in the ratio of 2:1 by mass. The temperature of the mixture is 27°C. Obtain the ratio of average kinetic energy per molecule and root mean square speed v_rms of the molecules of the two gases. Given: atomic mass of argon =39,9 U and molecular mass of chlorine = 70.9 u.
Answer:

Given

A flask contains Argon and Chlorine in the ratio of 2:1 by mass. The temperature of the mixture is 27°C.

atomic mass of argon =39,9 U and molecular mass of chlorine = 70.9 u

Average kinetic energy of a molecule of any ideal gas = \(\frac{3}{2}\)kT

1. As both argon and chlorine have the same temperature, the ratio of average kinetic energy per molecule of the two gases =1:1

2. Let m be the mass of a molecule of the gas.

Now, average kinetic energy per molecule = \(\frac{1}{2} m v_{\mathrm{rms}}^2\)

∴ \(\frac{1}{2} m_1 v_1^2=\frac{1}{2} m_2 v_2^2=\frac{3}{2} k T\)

or, \(\frac{v_1^2}{v_2^2}=\frac{m_2}{m_1}=\frac{M_2}{M_1}=\frac{70.9}{39.9}=1.7\)

where M is the atomic or molecular mass of the gas.

So, \(\frac{v_1}{v_2}=\sqrt{1.77}=1.33\)

Here, the composition of a mixture of gases is not relevant since,

⇒ \(\frac{v_1}{v_2}=\sqrt{\frac{\overline{M_2}}{M_1}}=\text { constant }\)

Question 23. Prove that the average kinetic energy of a molecule of an ideal gas is directly proportional to the absolute temperature of the gas.
Solution:

We know that the average kinetic energy of a molecule is directly proportional to the absolute temperature of the gas.

Let one gram mole of an ideal gas occupy a volume V at temperature T.

If m is the mass of each molecule of the gas, then M = m x N_A [where N_A is the Avogadro’s number]

If c is the rms speed of the gas molecules, then the pressure exerted by the ideal gas is p = \(\frac{1}{3} \rho c^2=\frac{1}{3} \frac{M}{V} c^2\)

Now from the equation pV = RT,

⇒ \(\frac{1}{3} M c^2=R T \quad or, M c^2=3 R T \quad or, [latex]\frac{1}{2} M c^2=\frac{3}{2} R T\)

or, \(\frac{1}{2} m N_A c^2=\frac{3}{2} R T \quad\left[because M=m N_A\right]\)

or, \(\frac{1}{2} m c^2=\frac{3}{2}\left(\frac{R}{N_A}\right) T=\frac{3}{2} k_B T\left[because k_B=\frac{R}{N_A}\right]\)

So, the average kinetic energy of translation per molecule of a gas

= \(\frac{1}{2} m c^2=\frac{3}{2} k_B T\)

Hence, the average kinetic energy of a molecule is directly proportional to the absolute temperature of the gas.

Question 24. The absolute temperature of a gas is increased 3 times. What will be the increase in root mean square velocity of the gas molecule?
Answer:

Given

The absolute temperature of a gas is increased 3 times.

rms velocity in terms of Boltzmann constant (k),

c = \(\sqrt{\frac{3 k T}{m}}\)

At temperature, \(T_1, c=\sqrt{\frac{3 k T_1}{m}}\)

Now, \(T_2=3 T_1\)

∴ \(c_2=\sqrt{\frac{3 k T_2}{m}}=\sqrt{\frac{3 k \times 3 T_1}{m}}=\sqrt{3} \cdot \frac{\sqrt{3 k T_1}}{m}\)

or, \(c_2=\sqrt{3} c\)

If the temperature of the gas increases 3 times, then the root mean square velocity of the gas particles increases by a factor of √3.

Work And Energy – Rotational Motion Of A Body In A Vertical Circle

Non-uniform circular motion: When a body of mass m is tied to a string and is rotated in a vertical circle, it will not rotate with uniform speed in that circular path. So, it is an example of a non-uniform circular motion.

The magnitude of its velocity increases when it descends from the highest point B of the circle to the lowest point A. Again, the magnitude of velocity gradually decreases when it rises up to the highest point from the lowest point of the circle.

During its rotation, the weight of the body always acts vertically downwards, but the direction of centripetal force changes continuously. Hence, the tension in the string does not remain constant.

At the highest point B of the circular path, tension in the string and the weight of the body together provide the necessary centripetal force for the rotation of the body. If the velocity of the body is v and the tension in the string is T₂ at point B, then \(T_2+m g=\frac{m v^2}{r}\)

or, \(T_2=\frac{m v^2}{r}-m g\)…(1)

Again, the tension in the string at the lowest point A on the circular path acts in the vertically upward direction, i.e., towards the center of the circle, but the weight of the body acts vertically downwards.

Applications Of Vertical Circular Motion In Physics

As a result, the difference between the tension in the string and the weight of the body provides the necessary centripetal force. If the velocity of the body is u and the tension in the string is T₁ at point A, then

⇒ \(T_1-m g=\frac{m u^2}{r}\)

or, \(T_1=\frac{m u^2}{r}+m g\)…(2)

If the tension in the string at the point B is zero, i.e., if T₂ = 0, then

⇒ \(\frac{m v^2}{r}-m g=0 \quad \text { or, } \frac{m v^2}{r}=m g\)

or, v = \(\sqrt{r g}\)…(3)

Hence, if the value of v is less than \(\sqrt{r g}\) at the highest point, then the tension in the string becomes negative, i.e., the string gets relaxed. As a result, the body descends in a parabolic path instead of rotating along a circular path.

Hence, the least velocity of the body at the highest point on the circular path to maintain the vertical circular motion should be \(\sqrt{r g}\). This least velocity is called the critical velocity.

Vertical Circular Motion Class 11 Physics Notes

Least Velocity At The Lowest Point On The Circular Path Necessary To Maintain The Critical Velocity: If the potential energies of the body at points A and B are V₁ and V₂, respectively, then

total energy at point A = \(\frac{1}{2} m u^2+V_1 \text {. }\)

Similarly, total energy at point B = \(\frac{1}{2} m v^2+V_2 \text {. }\)

According to the principle of conservation of energy, \(\frac{1}{2} m u^2+V_1=\frac{1}{2} m v^2+V_2\)

or, \(V_2-V_1=\frac{1}{2} m\left(u^2-v^2\right)\)…(4)

When a body of mass m attains a height h, the potential energy gained by it = mgh. In the given figure, the height of the point B with respect to the point A is 2r.

So, the change in potential energy = V₂ – V₁ = mg · 2r

∴ From equation (4) we get, mg \(\cdot 2 r=\frac{1}{2} m\left(u^2-v^2\right)\)

or, \(4 g r=u^2-v^2\)

or, \(u^2=4 g r+v^2=4 g r+g r\)

(the least velocity at \(B, v=\sqrt{g r}\))

or, \(u^2=5 g r\)

or, \(u=\sqrt{5 g r}\)…(5)

Energy Conservation In Vertical Circular Motion Class 11

For rotation in a vertical circle, this is the least value of u. It should be noted that the value of this least velocity is independent of the mass of the body.

For this last value of u, the minimum value of tension at point A can be determined from equation (2).

⇒ \(\left(T_1\right)_{\min }=\frac{m u_{\min }^2}{r}+m g=\frac{m \cdot 5 g r}{r}+m g \)

= \(5 m g+m g=6 \mathrm{mg}\)

or, \(\left(T_1\right)_{\min }=6 \times\) weight of the body…(6)

So, if a body is rotated in a vertical circle, then at the lowest point of the circle, the minimum tension in the string is 6 times the weight of the body.

Vertical Circular Motion Formula Class 11

Rotation Of A Bucket Full Of Water In A Vertical Circle: When a bucket full of water is made to rotate with high speed in a vertical circle, it is seen that at the highest point of the circular path, though the bucket is inverted, water from it does not spill out. It is clear that when the bucket is at the highest position, two forces act simultaneously on the water in the bucket:

1. Downward weight (mg) of water (m = mass of water).
2. The upward reaction of the centripetal force; if the velocity of the bucket at the highest position is v and the radius of the circular path is r, the value of this centripetal force acting on the bucket due to its rotation = \(\frac{m v^2}{r}.\)

Thus, when the upward force becomes greater than the force downward, water in the bucket cannot fall down. So, the condition for water to not fall down is, \(\frac{m v^2}{r}.\) ≥ mg or, v² ≥ rg.

Hence, the minimum value of v should be \(\sqrt{r g}\).

According to equation (6), when this bucket is rotated along a complete circular path, at the lowest position of the bucket, the tension acting on the hand will be 6 times the weight of the bucket filled completely with water. Hence, it is difficult to perform the experiment with a heavy bucket full of water. However, it is easier with a bucket or some other container containing a small amount of water.

Work And Energy – Rotational Motion Of A Body In A Vertical Circle Numerical examples

Example 1. A body of mass 1 kg is tied with a thread and is whirled in a vertical circle of radius 50 cm with a speed of 500 cm · s^-1. What will be the tension in, the thread at the highest and the lowest positions of the body?
Solution:

Given

A body of mass 1 kg is tied with a thread and is whirled in a vertical circle of radius 50 cm with a speed of 500 cm · s^-1

Speed of the body at every point on the circular path is the same and its value, v = 500 cm · s^-1 = 5 m · s^-1.

So, at every point on the circular path, centripetal force, F = \(\frac{m v^2}{r}=\frac{1 \times(5)^2}{0.5}=50 \mathrm{~N}\)

Weight of the body = mg = 1 x 9.8 = 9.8 N

At the highest position, the tension in the thread (T₁) and the weight of the body both act downwards and together they provide the necessary centripetal force.

Hence, F = mg+ T₁ or, T₁ = F- mg = 50 – 9.8 = 40.2 N

At the lowest position, the tension in the thread (T₂) acts in the upward direction but the weight acts downwards, and hence, in this case, (T₂ – mg) provides the necessary centripetal force.

So, T₂ – mg – F or, T₂ = F+ mg = 50 + 9.8 = 59.8 N.

Minimum Velocity For Vertical Circular Motion Class 11

Example 2. A particle of mass 100 g is suspended from the end of a weightless string of length 100 cm and is rotated in a vertical plane. The speed of the particle is 200 cm · s^-1 when the string makes an angle of θ = 60° with the vertical. Determine

1. The tension in the string when θ = 60° and
2. The speed of the particle at the lowest position. Acceleration due to gravity = 980 cm · s^-2.

Solution:

Given

A particle of mass 100 g is suspended from the end of a weightless string of length 100 cm and is rotated in a vertical plane. The speed of the particle is 200 cm · s^-1 when the string makes an angle of θ = 60° with the vertical.

1. The body is rotated in a vertical plane.

At point B, when the string makes an angle of 60° with the vertical, the velocity of the particle is v (say).

If the tension in the string is T, then T – \(mg \cos 60^{\circ}=\frac{m v^2}{r}\)

∴ T = \(m g \cos 60^{\circ}+\frac{m v^2}{r}\)

Here, v = \(200 \mathrm{~cm} \cdot \mathrm{s}^{-1} ; r=100 \mathrm{~cm} ; m=100 \mathrm{~g}\)

Real Life Examples Of Vertical Circular Motion Class 11

∴ T = \(100 \times 980 \times \frac{1}{2}+\frac{100 \times(200)^2}{100}\)

= \(8.9 \times 10^4 \mathrm{dyn} .\)

2. From the principle of conservation of energy we get, the kinetic energy of the body at the lowest point A = sum of the potential and kinetic energies at the point B

or, \(\frac{1}{2} m v_A^2=\frac{1}{2} m \nu^2+m g \cdot A C\)

(\(v_A\) = speed of the particle at the point A)

or, \(v_A^2=\nu^2+2 g \cdot A C\)

Here, \(A C=O A-O C=O A-O B \cos \theta\)

= \(l-l \cos \theta=100-100 \cos 60^{\circ}=50 \mathrm{~cm}\)

∴ \(v_A^2=(200)^2+2 \times 980 \times 50=13.8 \times 10^4\)

or, \(v_A=371.5 \mathrm{~cm} \cdot \mathrm{s}^{-1} \text {. }\)

Tension In Vertical Circular Motion Class 11

Example 3. A body slides down an inclined plane after being released from rest from a height h and finally, it describes a circle of radius r instead of travelling along a horizontal floor. For what minimum value of h, can the particle describe that motion? Ignore friction.
Solution:

Given

A body slides down an inclined plane after being released from rest from a height h and finally, it describes a circle of radius r instead of travelling along a horizontal floor.

After descending along the inclined plane, the body can describe the circular path if the velocity of the body at the lowest point B of the circular path is, at least, v = \(\sqrt{5 g r}\).

The kinetic energy of the body at the point B

= \(\frac{1}{2} m v^2=\frac{1}{2} m \cdot 5 g r=\frac{5}{2} m g r\)

The falling body will acquire this kinetic energy in exchange for the potential energy that it possesses at the height h.

So, \(\frac{5}{2} m g r\) = mgh or, h = \(\frac{5}{2}\)r

Derivation Of Vertical Circular Motion Class 11

Example 4. A body starts falling from the top of a smooth sphere of radius r. What angle does the body subtend at the center of the sphere when it just loses contact with the sphere and what will be its velocity then?
Solution:

Given

A body starts falling from the top of a smooth sphere of radius r.

Let the angle subtended by the body at the center of the sphere when it loses contact with the sphere be θ. The body just loses contact with the sphere when the component of gravitational force cannot provide the necessary centripetal force to the body so that it can continue in the circular path.

Numerical Problems On Vertical Circular Motion Class 11

So, according to mgcosθ = \(\frac{mv^2}{r}\)……(1)

(v = velocity of the body when it just loses contact with the sphere)

According to the principle of conservation of energy, \(\frac{1}{2}\)\({mv^2}\)= mgr(1-cosθ)

[OC = OA – r, OB = rcosθ, BC = OC- OB – r- rcosθ = r(1 – cosθ)]

or, v² = 2gr(1 – cosθ)…(2)

From equations (1) and (2) we get, mg\(\cos \theta=\frac{m}{r} \cdot 2 g r(1-\cos \theta)\)

or, \(\cos \theta=2(1-\cos \theta)\)

or, \(\cos \theta=\frac{2}{3} \quad \text { or, } \theta=\cos ^{-1} \frac{2}{3}=48.2^{\circ}\)

Again, \(v^2=2 g r(1-\cos \theta)=2 g r\left(1-\frac{2}{3}\right)=\frac{2}{3} g r \)

∴ v = \(\sqrt{\frac{2}{3} g r .}\)

Work And Energy – Elastic And Inelastic Collisions

The total momentum of a system of interacting bodies remains constant in the absence of an external force. But generally, the total kinetic energy of the system is not conserved. In most collisions, a fraction of the kinetic energy transforms into heat and sound.

• If the total momentum and the total kinetic energy of a system are conserved, the collision is termed as an elastic collision. The collision of two billiard balls on a smooth board is almost elastic. Collisions in atoms and molecules, or interactions involving protons, electrons, neutrons, etc., are assumed to be elastic.
• On the other hand, if the total momentum is conserved, but the total kinetic energy is not, it is an inelastic collision. Most practical collisions are inelastic.

Derivation Of One-Dimensional Elastic Collision Between Two Particles: Suppose m₁ and m₂ are the masses of two particles that are moving with velocities \(\overrightarrow{u_1}\) and \(\overrightarrow{u_2}\) respectively(ux > 1ÿ) in the same direction along a straight line. They collide elastically, and after collision, move along the same direction with velocities \(\overrightarrow{v_1}\) and \(\overrightarrow{u_2}\) respectively.

Since one-dimensional motion is considered here vector notation can be dropped. Only components can be used with signs to indicate direction.

From the law of conservation of momentum, \(m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2\)

or, \( m_1\left(u_1-v_1\right)=m_2\left(v_2-u_2\right)\)…(1)

In an elastic collision, the total kinetic energy of the particles will also be conserved.

Hence, kinetic energy before collision = kinetic energy after collision

or, \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\)

or, \(m_1\left(u_1^2-v_1^2\right)=m_2\left(v_2^2-u_2^2\right)\)…(2)

Now, (2) ÷(1) gives, \(u_1+v_1=v_2+u_2 \quad \text { or, } u_1-u_2=v_2-v_1\)…(3)

Hence, \(v_2=u_1+v_1-u_2\)

Substituting the value of \(v_2\) in equation (1) \(m_1\left(u_1-v_1\right)=m_2\left(u_1+v_1-2 u_2\right)\)

or, \(u_1\left(m_1-m_2\right)+2 u_2 m_2=v_1\left(m_1+m_2\right)\)

or, \(v_1=\frac{m_1-m_2}{m_1+m_2} u_1+\frac{2 m_2}{m_1+m_2} u_2\)

Similarly, taking the value of \(v_1\) from equation (3) and substituting it in equation (1), \(v_2=\frac{m_2-m_1}{m_1+m_2} u_2+\frac{2 m_1}{m_1+m_2} u_1\)

It is important to note that, equations (4) and (5) are symmetrical against interchange of the first and the second particles i.e., if the subscripts 1 and 2 are interchanged same equations (4) and (5) will be obtained.

Derivation Of One-Dimensional Elastic Collision Between Two Particles Special Cases:

1. Particles Are Of Equal Mass: In this case m₁ = m₂, hence from equations (4) and (5), v₁ = u₂ and v₂ = u₁.

Particles exchange their velocities after the collision.

2. Particles Are Of Equal Mass, And The Second Particle Is Initially At Rest: Here, m₁ = m₂ and u₂ = 0. Hence v₁ = 0 and v₂= u₁, from equations (4) and (5). The first particle comes to rest and the second particle gains the velocity of the first, after collision. Such events are frequent in games like billiards.

3. Particles Are Of Equal Mass, And The Second Particle Is Initially At Rest: Here, m₁ = m₂ and u₂ = 0. Equations (4) and (5) thus change as,

⇒ \(v_1=\frac{m_1-m_2}{m_1+m_2} u_1 \text {, and } v_2=\frac{2 m_1}{m_1+m_2} u_1\)

If m₁ and m₂ have different values, the first particle will not stop after collision. Hence, when a striker hits a stationary coin in a game of carrom, both the striker and the coin move after collision.

Class 11 Physics Elastic and Inelastic Collision notes

4. The First Particle Is Much Heavier Than The Second Particle And The Second Particle Is Initially At Rest.

In this case, m₁ >> m₂ and u₂ = 0.

Hence, m₁ – m₂ ≅ m₁ + m₂ ≅ m₁

∴ v₁ ≅ u₁ and v_{2 ≅} 2u₁

Therefore, after collision, the velocity of the first (massive) particle practically remains unchanged; but the second particle gains a velocity equal to almost twice the initial velocity of the first particle. In a collision, the velocity acquired by a body cannot be greater than twice the velocity of the collider.

5. The Second Particle Is Much Heavier Than The First And Is Initially At Rest: Here, m₂ >>m₁ and u₂ = 0. Hence m₁ -m₂ ≈ -m₂ and m₁ + m₂ ≈ m₂.

Values of v₁ and v₂ are thus v₁ ≈ -u₁ and v₂ = 0.

Hence, after the collision, the massive body will continue to be at rest; and the collider will recoil with the same magnitude of velocity. A collision between a tennis ball and the earth’s surface is of this type.

Work And Energy – Elastic Collisions Numerical Examples

Example 1. Two particles of equal mass moving towards each other with velocities 20 m · s^-1 and 30 m · s^-1 collide. If the collision is elastic, find their velocities after the collision.
Solution:

Given

Two particles of equal mass moving towards each other with velocities 20 m · s^-1 and 30 m · s^-1 collide. If the collision is elastic

The particles are moving towards each other. If the velocity (u₁) of one is 20 m · s^-1, then the velocity (u₂) of the other particle is -30 m · s^-1.

After the collision, suppose the velocities are v₁ and v₂ respectively

From the law of conservation of linear momentum, m x 20 – m x 30 = mv₁ + mv₂

or, v₁ + v₂ = -10…(1)

For elastic collision, v₂ – v₁ = u₁ – u₂

or, v₂ – v₁ = 20-(-30) = 50…..(2)

Solving equations (1) and (2), v₁ = -30 m · s^-1 and v₂ = 20 m · s^-1.

Difference between elastic and inelastic collision Class 11

Example 2. Three balls A, B, and C of masses m₁, m_2, and m₃ respectively are kept at rest along a straight line. Now A moving in that straight line with velocity u₁ strikes B and then B moving with velocity u₂ strikes C. As a result velocity of C becomes u₃. If the collisions are elastic, show that u₃ ≅ 4u₁, when m₁ >> m₂ and m₂ >>m₃. In case A hits C directly, will the velocity of C be higher or lower?
Solution:

Given

Three balls A, B, and C of masses m₁, m_2, and m₃ respectively are kept at rest along a straight line. Now A moving in that straight line with velocity u₁ strikes B and then B moving with velocity u₂ strikes C. As a result velocity of C becomes u₃. If the collisions are elastic,

Suppose A acquires a velocity v₁ after collision with B. From the law of conservation of linear momentum, for collision between A and B, m₁u₁ = m₁v₁ + m₂u₂

or, m₁(u₁ – v₁) = m₂u₂…..(1)

From the law of conservation of kinetic energy for elastic collision \(\frac{1}{2} m_1 u_1^2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 u_2^2\)

or, \(m_1\left(u_1^2-v_1^2\right)=m_2 u_2^2\)….(2)

Dividing equation (2) by (1), \(u_1+v_1=u_2 \text { or, } v_1=u_2-u_1\)

Inserting the value of \(v_1\) in equation (1), \(m_1\left(2 u_1-u_2\right)=m_2 u_2 \quad \text { or, } 2 m_1 u_1=\left(m_1+m_2\right) u_2\)

Hence, \(u_2=\frac{2 m_1}{m_1+m_2} \cdot u_1=\frac{2}{1+\frac{m_2}{m_1}} \cdot u_1\)

As \(m_1 \gg m_2, \frac{m_2}{m_1} \ll 1\); hence, \(1+\frac{m_2}{m_1} \approx 1\).

Thus, \(u_2 \approx 2 u_1\).

Similarly, for the collision of B with C, \(u_3 \approx 2 u_2\). Thus \(u_3 \approx 4 u_1\).

But, for the direct collision of A with C, the velocity gained by C, u₃‘ ≈ 2u₁

∴ u₃‘ is less than u₃.

Hence, in case of a direct collision between A and C, the speed of C will be less.

Laws of conservation in elastic and inelastic collision Class 11

One-Dimensional Inelastic Collision Between Two Particles: In an inelastic collision, the total kinetic energy is not conserved, but the total momentum is conserved.

• Two particles are moving in the same direction in a straight line with velocities u₁ and u₂ respectively (u₁ > u₂). Before the collision, the distance between the two particles will decrease, and their velocity of approach will be = (u₁ – u₂).
• After collision, their separation increases with time i.e., (v₂ > v₁), where v₁ = velocity of first particle, v₂ = velocity of second particle after the impact. Therefore, ( v₂ – v₁) = the velocity of separation.

Coefficient Of Restitution: Coefficient of restitution is defined as the ratio of the velocity with which the two bodies separate after collision to the velocity of their approach before collision,

i.e., e = \(\frac{\text { relative velocity of separation after collision }}{\text { relative velocity of approach before collision }}\)

= \(\frac{v_2-v_1}{u_1-u_2}\)…..(2)

The value of e is practically constant for two specific bodies.

Perfectly Inelastic Collision: In this type of collision the two colliding bodies stick together and move as a single body, i.e., they move with a common velocity. A perfectly inelastic collision has been shown.

Suppose, two bodies of masses m₁ and m₂, moving with velocities u₁ and u₂ respectively in the same direction along a straight line, collide perfectly inelastically. After the collision, they stick together and move with velocity v along the same straight line.

From the principle of conservation of linear momentum, we get, \(m_1 u_1+m_2 u_2=\left(m_1+m_2\right) v\)

or, \(v^{\prime}=\frac{m_1 u_1+m_2 u_2}{m_1+m_2}\)…(2)

Perfectly Inelastic Collision Loss Of Kinetic Energy: Total kinetic energy before collision = \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2\)

Total kinetic energy after collision = \(\frac{1}{2}\left(m_1+m_2\right) v^2\)

∴ Loss of kinetic energy

= \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2-\frac{1}{2}\left(m_1+m_2\right) v^2\)

= \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2-\frac{1}{2}\left(m_1+m_2\right)\left(\frac{m_1 u_1+m_2 u_2}{m_1+m_2}\right)^2\)

= \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2-\frac{1}{2} \frac{\left(m_1 u_1+m_2 u_2\right)^2}{m_1+m_2}\)

= \(\frac{1}{2\left(m_1+m_2\right)}\)

= \(\frac{1}{2\left(m_1+m_2\right)}\) (\(m_1^2 u_1^2+m_1 m_2 u_1^2+m_1 m_2 u_2^2\))

= \(\frac{m_1 m_2}{2\left(m_1+m_2\right)}\left[u_1^2+u_2^2-2 u_1^2 u_2^2\right]\)

= \(\frac{m_1 m_2}{2\left(m_1+m_2\right)} \cdot\left(u_1 u_1^2-m_2^2 u_2^2-2 m_1 m_2 u_1 u_2 u_2\right]\)

Here (u₁– u₂) is the relative velocity of the two bodies before collision. So the loss of kinetic energy is proportional to the square of this relative velocity. Again if u₂ = 0 i.e., if the second body is at rest before collision the loss of kinetic energy becomes maximum.

Elastic and inelastic collision Class 11 NCERT solutions

Partially Elastic Collision Definition: In this type of collision the two bodies do not stick, but move separately along the same straight line with different velocities. Here momentum remains conserved while the total kinetic energy decreases.

The relative velocity of the two bodies before collision = u₁ – u₂ and that after collision = v₂ – v₁.

So, the coefficient of restitution, e = \(\frac{v_2-v_1}{u_1-u_2}\)…(4)

According to the law of conservation of momentum, \(m_1 u_1+m_2 u_2=m_1 \nu_1+m_2 v_2\)…(5)

Now from equation (4) we have, \(e\left(u_1-u_2\right)=v_2-v_1\)

Multiplying the above equation by \(m_2\) we have, \(e m_2 u_1-e m_2 u_2=m_2 \nu_2-m_2 v_1\)…(6)

Subtracting equation (6) from equation (5) we get, \(u_1\left(m_1-e m_2\right)+u_2(1+e) m_2=\left(m_1+m_2\right) v_1\)

∴ \(\nu_1=\frac{\left(m_1-e m_2\right) u_1+(1+e) m_2 u_2}{m_1+m_2}\)…(7)

Similarly, \(v_2=\frac{\left(m_2-e m_1\right) u_2+(1+e) m_1 u_1}{m_1+m_2}\)

Elastic and inelastic collision Class 11 problems with solutions

Partially Elastic Collision Loss Of Kinetic Energy: \(\left(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2\right)-\left(\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\right)\)

= \(\frac{1}{2\left(m_1+m_2\right)}\left[\left(m_1+m_2\right)\left(m_1 u_1^2+m_2 u_2^2\right)-\right.\) \(\left.\quad\left(m_1+m_2\right)\left(m_1 v_1^2+m_2 v_2^2\right)\right]\)

Now, \(\left(m_1+m_2\right)\left(m_1 u_1^2+m_2 u_2^2\right)\)

= \(m_1^2 u_1^2+m_2^2 u_2^2+m_1 m_2\left(u_1^2+u_2^2\right)\)

= \(\left(m_1 u_1+m_2 u_2\right)^2+m_1 m_2\left(u_1-u_2\right)^2\)

Similarly, \(\left(m_1+m_2\right)\left(m_1 v_1^2+m_2 v_2^2\right)\)

= \(\left(m_1 v_1+m_2 v_2\right)^2+m_1 m_2\left(v_1-v_2\right)^2\)

= \(\left(m_1 u_1+m_2 u_2\right)^2+m_1 m_2 e^2\left(u_1-u_2\right)^2\)

(because \(v_2-v_1=e\) \((u_1-u_2)\))

So, the loss of kinetic energy = \(\frac{1}{2\left(m_1+m_2\right)}[\left(m_1 u_1+m_2 u_2\right)^2+m_1 m_2\left(u_1-u_2\right)^2\)

– \((m_1 u_1+m_2 u_2)^2-m_1 m_2 e^2\left(u_1-u_2\right)^2\)

= \(\frac{m_1 m_2}{2\left(m_1+m_2\right)}\left(1-e^2\right)\left(u_1-u_2\right)^2 \)…(9)

1. If e = 1, i.e., if the collision is perfectly elastic, then the loss of kinetic energy = 0, i.e., in case of a perfectly elastic collision kinetic energy remains conserved.
2. If e = 0 , i.e., if the collision is perfectly inelastic, kinetic energy decreases and the loss of kinetic energy = \(\frac{m_1 m_2}{2\left(m_1+m_2\right)}\left(u_1-u_2\right)^2\)
3. For partially elastic collision, 0 < e < 1.

Inelastic Collisions Numerical Examples

Example 1. Two bodies of masses 5 kg and 10 kg move towards each other with velocities 10 m · s^-1 and 14 m s^-1 respectively. If the coefficient of restitution is 0.8, find their velocities after the collision.
Solution:

Given

Two bodies of masses 5 kg and 10 kg move towards each other with velocities 10 m · s^-1 and 14 m s^-1 respectively. If the coefficient of restitution is 0.8

Let u₁ and u₂ respectively be the velocities of the first and the second body before the collision. After the collision, their velocities will be v₁ and v₂ respectively.

From the law of conservation of linear momentum \(m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2\)

Here, \(m_1=5 \mathrm{~kg}, \quad m_2=10 \mathrm{~kg}, \quad u_1=10 \mathrm{~m} \cdot \mathrm{s}^{-1}\) and \(u_2=-14 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

[let us assume \(u_1\) to be taken along positive x-axis and \(u_2\) along negative x-axis]

∴ \(5 \times 10+10 \times(-14)=5 v_1+10 v_2\)

or, \(v_1+2 v_2=-18\)….(1)

Also, \(e=\frac{v_2-v_1}{u_1-u_2}\) or, \(0.8=\frac{v_2-v_1}{10-(-14)}\)

or, \(v_2-v_1=0.8 \times 24=19.2\)…..(2)

Hence, from (1) and (2), \(3 v_2=1.2 \text { or, } v_2=\frac{1.2}{3}=0.4 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

and \(v_1=-18.8 \mathrm{~m} \cdot \mathrm{s}^{-1}\) which means after the collision the 5 kg mass advances along the negative x-axis and the 10 kg mass goes along positive x-axis.

Real life examples of elastic and inelastic collision Class 11

Example 2. Two bodies of masses 1 kg and 0.5 kg towards each other with velocities 10 cm · s^-1 and 5 cm · s^-1 respectively. After the collision, the bodies coalesce (Join together). Find the common velocity after collision and the loss in kinetic energy.
Solution:

Given

Two bodies of masses 1 kg and 0.5 kg towards each other with velocities 10 cm · s^-1 and 5 cm · s^-1 respectively. After the collision, the bodies coalesce

Let the velocity of the combined mass after collision be v. From the law of conservation of momentum, \(m_1 u_1+m_2 u_2=\left(m_1+m_2\right)v\)

or, \(1 \times 0.1+0.5 \times(-0.05)=(1+0.5) v\)

or, \(0.1-0.025=1.5 v \quad \text { or, } v=\frac{0.075}{1.5}=0.05 \mathrm{~m} \cdot \mathrm{s}^{-1} .\)

This implies that the velocity of the combined mass is along the direction of the initial velocity of the 1kg mass.

The initial kinetic energy of the bodies = \(\frac{m_1 u_1^2}{2}+\frac{m_2 u_2^2}{2}=\frac{1}{2} \times 1 \times(0.1)^2+\frac{1}{2} \times(0.5) \times(0.05)^2\)

= \(5.625 \times 10^{-3} \mathrm{~J}\)

The final kinetic energy of the combined mass after the collision = \(\left(m_1+m_2\right) \frac{v^2}{2}\)

= \(\frac{1}{2} \times(1+0.5) \times(0.05)^2=1.875 \times 10^{-3} \mathrm{~J}\)

∴ Loss in kinetic energy = \((5.625-1.875) \times 10^{-3}=3.75 \times 10^{-3} \mathrm{~J} \text {. }\)

Elastic and inelastic collision Class 11 important questions

Example 3. A car of mass 2000 kg collides with a truck of mass 10⁴ kg moving at 48 km • h^-1. After the collision, the car rides up the truck, and the truck-car combination moves at 15 km • h^-1. What was the velocity of the car before the collision?
Solution:

Given

A car of mass 2000 kg collides with a truck of mass 10⁴ kg moving at 48 km • h^-1. After the collision, the car rides up the truck, and the truck-car combination moves at 15 km • h^-1

The collision is inelastic as both bodies move together after the collision. Suppose a body of mass m, moving with velocity u, collides inelastically along a straight line with a body of mass M and velocity v. After collision, the two masses combine and move with velocity V. Applying the law of conservation of momentum,

mu+Mv = (m + M)V or, mu – (m + M)V-Mv

or, u = \(\frac{m+M}{m} V-\frac{M}{m} \nu=\left(1+\frac{M}{m}\right) V-\frac{M}{m} \nu\)

Here \(m=2000 \mathrm{~kg}, \quad \nu=48 \mathrm{~km} \cdot \mathrm{h}^{-1}, \quad M=10000 \mathrm{~kg}\),

V = \(15 \mathrm{~km} \cdot \mathrm{h}^{-1}\)

∴ \(\frac{M}{m}=\frac{10000}{2000}=5\)

u = (1 + 5) x 15- 5 x 48 = 90 – 240 = -150 km · h^-1

The negative sign indicates that, before the collision, the car was moving in the direction opposite to that of the truck.

Example 4. A ball of mass 100 g was thrown vertically upwards with a velocity of 49 m · s^-1. At the same time another identical ball was dropped, to fall along the same path from a height of 98 m. After some time, the two balls collided and got stuck together. This combined mass then fell to the ground. How long was the combined mass in motion?
Solution:

Given

A ball of mass 100 g was thrown vertically upwards with a velocity of 49 m · s^-1. At the same time another identical ball was dropped, to fall along the same path from a height of 98 m. After some time, the two balls collided and got stuck together. This combined mass then fell to the ground.

Suppose the balls collide at a height h above the ground in time t₁. Analysing the upward motion of the 1st ball, we get, h = \(49 t_1-9.8 t_1^2 / 2\)…….(1)

Analysing the downward motion of the 2nd ball, we get, 98-h = \(9.8 t_1^2 / 2\)……(2)

From equations (1) and (2), 98 = 49t₁ or, t₁ = 2 s

At the time of the collision, let the velocity of the 1st ball be v₁ and that of the 2nd ball be v₂.

∴ v₁ = 49 – 9.8 x 2 = 29.4 m · s^-1 (upward) and

v₂ = 9.8 x 2 = 19.6 m · s^-1 (downward)

After the collision, let the velocity of the combined mass be V. Then according to the law of conservation of momentum, 0.1 x 29.4 – 0.1 x 19.6 = 2 x 0.1 x V [indicating downward motion with a negative sign]

or, V = 4.9 m · s^-1 (upward)

From equation (1), we get, h = 49 x 2 – 9.8 x (2)²/2 = 78.4 m

If the combined mass was in motion for a time t, then from the relation h = ut+ 1/2 gt², we get,

-78.4 = 4.9t – 1/2 x 9.8 t², or, t² – t- 16 = 0

∴ t = \(\frac{1}{2}(1 \pm \sqrt{1+4 \times 1 \times 16})\)

As t cannot be negative, we have, t = 4.53 s

Elastic and inelastic collision derivation Class 11

Example 5. A bullet of mass 50 g is fired into a wooden block of mass 2 kg resting on a smooth table surface. The bullet enters at 50 m · s^-1 and gets embedded in the block. Find the final velocity of the block. Find the initial and the final kinetic energy of the block-bullet system.
Solution:

Given

A bullet of mass 50 g is fired into a wooden block of mass 2 kg resting on a smooth table surface. The bullet enters at 50 m · s^-1 and gets embedded in the block.

From the law of conservation of momentum, m₁v = (m₁ + m₂)V

or, V = \(\frac{m_1 \nu}{m_1+m_2}\)….(1)

Here, m₁ = 50 g = 0.05 kg, v = 50 m ·  s^-1 and m₂ = 2 kg.

∴ The final velocity of the block, V = \(\frac{0.05 \times 50}{0.05+2}=1.22 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Initial kinetic energy of the system, \(E_i=\frac{1}{2} \times 0.05 \times 50^2=62.5 \mathrm{~J}.\)

Final kinetic energy, \(E_f=\frac{1}{2} \times(2+0.05) \times(1.22)^2=1.52 \mathrm{~J}\)

Elastic and inelastic collision Class 11 numericals

Example 6. A bullet of mass 250 g, moving with a horizontal velocity of 400 m · s^-1, gets embedded in a target The target of mass 4.75 kg can move freely. Find the loss of kinetic energy due to this collision. What happens to this energy loss?
Solution:

Given

A bullet of mass 250 g, moving with a horizontal velocity of 400 m · s^-1, gets embedded in a target The target of mass 4.75 kg can move freely.

Mass of the bullet, m = 250 g = 0.25 kg, the velocity of the bullet, v = 400 m · s^-1, and the mass of the target, M = 4.75 kg.

After the impact, the target and the bullet both move with a velocity V (say).

From the law of conservation of momentum, mv = (M+ m)V

∴ V = \(\frac{m v}{M+m}=\frac{0.25 \times 400}{0.25+4.75}=20 \mathrm{~m} \cdot \mathrm{s}^{-1} .\)

Kinetic energy of the target and the bullet after collision = \(\frac{1}{2}(M+m) V^2=\frac{1}{2}(4.75+0.25) \times 20^2=1000 \mathrm{~J}\)

Kinetic energy of the bullet before the collision,

= \(\frac{1}{2} m v^2=\frac{1}{2} \times 0.25 \times(400)^2=20000 \mathrm{~J}\).

Hence, the kinetic energy lost in collision = 20000-1000 = 19000 J.

This kinetic energy transforms into heat and sound energy.

Collisions In Two Dimensions: Let a particle of mass m₁ moving with a velocity u₁ along AO, collide at point O with another particle of mass m₂ moving with velocity u₂ along BO. The point O is chosen as the origin, the direction of AO as the x-axis, and a perpendicular direction on the plane of AO and BO as the y-axis.

Before the collision, it is evident that, the x-component of momentum of the 1st particle = m₁u₁,

y -component of momentum of the 1st particle = 0,

x -component of momentum of the 2nd particle = -m₂u₂ cosθ,

y -component of momentum of the 2nd particle = m₂u₂ sinθ.

So, there is no component of momentum perpendicular to the xy-plane, i.e., along the z-direction. We know that, in both elastic and inelastic collisions, the total momentums of the particles remain conserved.

Thus, even after the collision between the two particles, there will be no z-component of momentum. This means that every two-particle collision, in general, is two-dimensional, i.e., such a collision is always confined in a plane.

In collision experiments, usually, a beam of incident particles hits a stationary target. After the collision, the first particle is observed by placing detector D in a definite orientation, say, at right angles with the direction of the incident beam.

In the figure, m₁, m₂: masses of the particles; u₁= velocity of m₁ before collision; u₂ = 0 = velocity of m₂ before collision;

v₁ = velocity of m₁ after collision deviated by 90°;

v₂ = velocity of m₂ after collision;

θ = angle made by v₂ with the direction of the incident beam.

Now, we may apply the principle of conservation of momentum, with the choice of the x and y-axes as shown

In the figure, x -direction: \(m_1 u_1+0=0+m_2 v_2 \cos \theta\)

or, \(m_2 v_2 \cos \theta=m_1 u_1\)…(1)

y-direction: \(0+0=m_1 v_1-m_2 v_2 \sin \theta\)

or, \(m_2 v_2 \sin \theta=m_1 v_1\)..(2)

Squaring and adding equations (1) and (2), \(m_2 v_2=m_1 \sqrt{u_1^2+v_1^2} \text { or, } v_2=\frac{m_1}{m_2} \sqrt{u_1^2+v_1^2}\)…(3)

Again, dividing equation (2) by equation (1), \(\tan \theta=\frac{v_1}{u_1} \quad \text { or, } \theta=\tan ^{-1} \frac{v_1}{u_1}\)…(4)

Usually, m₁, m_2, and are known prior to the experiment, and v₁ is measured by the detector D. So the magnitude and direction of the velocity (v₂) of the second particle after collision can be calculated using equations (3) and (4).

General Analysis Of Two-Dimensional Collisions: We have already seen that the motion of two particles, both before and after they collide with each other, is confined in a plane. Let that plane be chosen as the xy-plane. We assume that the magnitudes and the directions of the velocities (i.e., of the momenta) of the two particles, before the collision, are known beforehand.

Then, four unknown quantities, associated with the collision, are to be solved. They are the magnitudes and the directions of the velocities of the two particles after the collision.

If the collision is elastic, we can construct at most three equations from the conservation principles:

1. Conservation Of Momentum Along The X-Axis,
2. Conservation Of Momentum Along The Y-Axis,
3. Conservation Of Kinetic Energy

These three equations are not sufficient to solve for four unknown quantities. If the collision is inelastic, the kinetic energy is not conserved. Then we have only two equations at hand. So, for a complete analysis of a two-particle collision, we should have some information on the particles after the collision.

• For example, in the collision experiment described above, we had placed a detector in such a way—at right angles to the initial direction of motion of one particle—that the final direction of the velocity of that particle was already assigned. Moreover, the detector could measure the magnitude of its velocity.
• So, we had to solve for only two unknown quantities—the magnitude and direction of the velocity of the second particle. So, only two equations were sufficient— equations obtained from the momentum conservation along the x- and the y-axes. Even the kinetic energy equation was not necessary; so the treatment was applicable to elastic as well as inelastic collisions.
• One other point is to be noted. In general, both the particles may be in motion before the collision. However, the collision may be observed by assuming one of the particles to be at rest.

The particle 2 is at rest; then the velocity of particle 1 is actually its relative velocity with respect to particle 2. This means that the frame attached to particle 2 has been taken as the frame of reference. So, there is no loss of generality if we describe a two-particle collision as a moving particle colliding with a stationary target.

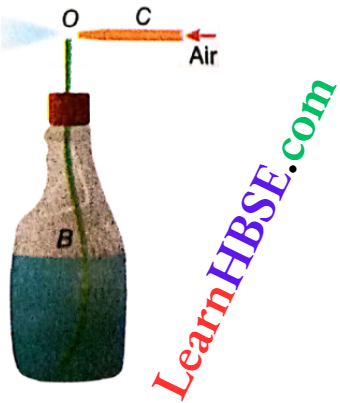
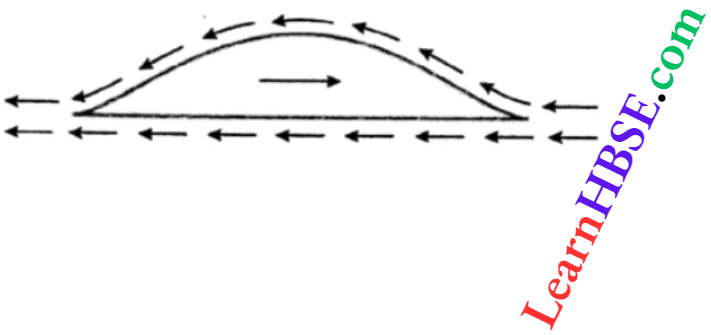
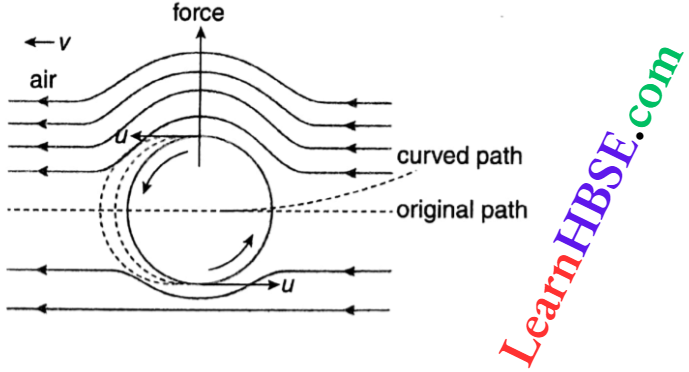
Expansion Of Gases Relation Between Pressure, Temperature And Density

Relation Between Pressure, Temperature And Density:

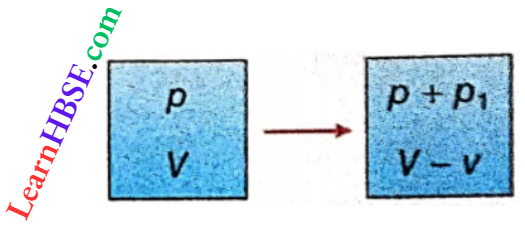
Let an ideal gas is taken of molecular weight M (say).

For m₁ mass of the gas, the volume and density be V₁ and ρ₁, respectively at a temperature T₁ K. When its mass is m₂ the volume and density are V₂ and ρ₂ respectively at T₂ K.

∴ \(V_1=\frac{m_1}{\rho_1} \text { and } V_2=\frac{m_2}{\rho_2}\)

If p₁ and p₂ are the pressures at those temperatures, then from the equation pV = nRT = m/M RT we have,

⇒ \(\frac{p_1 V_1}{m_1 T_1}=\frac{p_2 V_2}{m_2 T_2}\) [since for a particular gas M is constant]

or, \(\frac{p_1}{\rho_1 T_1}=\frac{p_2}{\rho_2 T_2}\)

∴ \(\frac{p}{\rho T}=\) constant

1. If the pressure is a constant, \(\rho_1 T_1=\rho_2 T_2 \text { i.e., } \rho T=\text { constant or, } \rho \propto \frac{1}{T}\)

i.e., at constant pressure, the density of a gas is inversely proportional to Its absolute temperature.

2. If the temperature is a constant,

i.e., at a constant temperature, the density of a gas is directly proportional to its pressure.

Expansion Of Gases Relation Between Pressure, Temperature And Density Numerical Examples

Example 1. Temperature and pressure on top of a hill are 7°C and 70 cmHg, and the corresponding values at its base are 27°C and 76 cmHg. Compare the densities of air at the top and the base of the hill.
Solution:

Given

Temperature and pressure on top of a hill are 7°C and 70 cmHg, and the corresponding values at its base are 27°C and 76 cmHg.

We use the relation \(\frac{p_1}{\rho_1 T_1}=\frac{p_2}{\rho_2 T_2}\)

Here, p₁ = 70 cmHg, T₁ = 273 + 7 = 280 K, p₂ = 76 cmHg and T₂ = 273 + 27 = 300 K.

⇒ \(\frac{70}{\rho_1 \times 280}=\frac{76}{\rho_2 \times 300} \text { or, } \frac{\rho_1}{\rho_2}=\frac{300 \times 70}{76 \times 280}=\frac{75}{76} \text {. }\)

Relation Between Pressure And Density In Fluids

Example 2. Density of argon at 27°C and 76 cmHg pressure Is 1.6 g · L^-1. An electric bulb of volume 200 cm3 is filled with argon. The pressure of the gas inside the bulb is 75 cmHg and the average temperature is 127°C. Find the mass of argon gas in the bulb.
Solution:

Given

Density of argon at 27°C and 76 cmHg pressure Is 1.6 g · L^-1. An electric bulb of volume 200 cm3 is filled with argon. The pressure of the gas inside the bulb is 75 cmHg and the average temperature is 127°C.

Let the density of the gas in the bulb at a pressure of 75 cmHg and at 127°C =ρ₂

Here, p₁ = 76 cmHg, ρ₁ = 1.6 g · L^-1,

T₁ = 273 + 27 = 300 K

p₂ = 75 cmHg,

T₂ = 273 + 127 = 400 K

From the relation \(\frac{p_1}{\rho_1 T_1}=\frac{p_2}{\rho_2 T_2}\) we get,

⇒ \(\frac{76}{1.6 \times 300}=\frac{75}{\rho_2 \times 400}\)

∴ \(\rho_2=\frac{75 \times 1.6 \times 300}{76 \times 400}=1.184 \mathrm{~g} \cdot \mathrm{L}^{-1}\)

∴ Mass of argon gas of volume 200cm³

= \(\frac{200}{1000} \times 1.184=0.2368 \mathrm{~g} .\)

Example 3. At a place, air pressure is 75 cmHg and the temperature is 27°C. At another place, the respective values are 70 cmHg and 17°C. Compare the densities of air in the two places.
Solution:

Given

At a place, air pressure is 75 cmHg and the temperature is 27°C. At another place, the respective values are 70 cmHg and 17°C.

We have, \(\frac{p_1}{\rho_1 T_1}=\frac{p_2}{\rho_2 T_2}\)

Given, p₁ = 75 cmHg, T₁ = 273 + 27 = 300 K, p₂ = 70 cmHg

and T₂ = 273 + 17 = 290 K

∴ \(\frac{75}{\rho_1 \times 300}=\frac{70}{\rho_2 \times 290} \text { or, } \frac{\rho_1}{\rho_2}=\frac{75 \times 290}{300 \times 70}=\frac{29}{28}\)

∴ \(\rho_1: \rho_2=29: 28\)

Pressure And Density Relation In Liquids

Example 4. When an air bubble rises from the bottom of a lake to the upper surface, its diameter increases from 1 mm to 2 mm. If the atmospheric pressure is 76 cmHg, calculate the depth of the lake. Density of mercury is 13.6 g · cm^-3.
Solution:

Given

When an air bubble rises from the bottom of a lake to the upper surface, its diameter increases from 1 mm to 2 mm. If the atmospheric pressure is 76 cmHg,

Density of mercury is 13.6 g · cm^-3.

Let the depth of the lake be h cm.

Pressure on the air bubble, at the bottom of the lake, p₁ = atmospheric pressure + pressure of water at depth h = (76 x 13.6 x 981 + h x 1 x 981) dyn · cm^-2, and pressure at the surface of the lake, p₂ = atmospheric pressure = 76 x 13.6 x 981 dyn · cm^-2

Volumes of the bubble: at the bottom, \(V_1=\frac{4}{3} \pi\left(\frac{1}{20}\right)^3 \mathrm{~cm}^3\)

at the top, \(V_2=\frac{4}{3} \pi\left(\frac{1}{10}\right)^3 \mathrm{~cm}^3\)

Using Boyle’s law: p₁ V₁ = p₂ V₂, we get,

(h x 1 x 981 + 76 x 13.6 x 981) x \(\times \frac{4}{3} \pi\left(\frac{1}{20}\right)^3\)

= 76 x 13.6 x 981 x \(\times \frac{4}{3} \pi\left(\frac{1}{10}\right)^3\)

or, (h x 76 x 13.6) x 1/8 = 76 x 13.6

or, h = 76 x 13.6 x 8 – 76 x 13.6

∴ The lake is 7235.2 cm or 72.352 m deep

Difference Between Pressure And Density In Physics

Example 5. An electronic vacuum tube is constructed and sealed at 27°C and 1.2 x 10^-6 cm Hg pressure. The tube has a volume of 100 cm³. Calculate the number of gas molecules left In the tube. Avogadro number is 6.02 x 10²³, and the gas occupies a volume of 22.4 litres at STP.
Solution:

Given

An electronic vacuum tube is constructed and sealed at 27°C and 1.2 x 10^-6 cm Hg pressure. The tube has a volume of 100 cm³.

Avogadro number is 6.02 x 10²³, and the gas occupies a volume of 22.4 litres at STP

Molar density at STP = \(\frac{6.02 \times 10^{23}}{22.4 \times 10^3} \text { molecules } \cdot \mathrm{cm}^{-3}\)

Let the number of molecules left in the tube, after sealing, be n.

From gas equation we have, \(\frac{p_1}{\rho_1 T_1}=\frac{p_2}{\rho_2 T_2}\)

Here, \(p_1=1.2 \times 10^{-6} \mathrm{cmHg}\)

⇒ \(\rho_1=\frac{n}{100} \text { molecules } \cdot \mathrm{cm}^{-3}\)

⇒ \(T_1=273+27=300 \mathrm{~K} \text {, }\)

⇒ \(p_2=76 \mathrm{cmHg} \text {, }\)

⇒ \(\rho_2=\frac{6.02 \times 10^{23}}{22.4 \times 10^3} \text { molecules } \cdot \mathrm{cm}^{-3}\)

and \(T_2=273 \mathrm{~K}\)

∴ \(\frac{1.2 \times 10^{-6}}{\frac{n}{100} \times 300}=\frac{76}{\frac{6.02 \times 10^{23}}{22.4 \times 10^3} \times 273}\)

i.e., n = \(\frac{1.2 \times 10^{-6} \times 100 \times 6.02 \times 10^{23} \times 273}{300 \times 76 \times 22.4 \times 10^3}\)

= \(3.86 \times 10^{13} \text {. }\)

Example 6. While constructing a bulb of volume 250 cm³, it is sealed at 27° C temperature and 10^-3 mmHg pres-sure. Find the number of gas molecules in the bulb. Avogadro number = 6.0 x 10²³.
Solution:

Given

While constructing a bulb of volume 250 cm³, it is sealed at 27° C temperature and 10^-3 mmHg pres-sure.

Volume of air inside the bulb, V₁ = 250 cm³; pressure of air, p₁ = 10^-3 mmHg = 10^-4 cmHg; temperature T₁ = 27 + 273 = 300 K.

Let at STP the volume of air = V₂ cm³; p₂ = 76 cmHg; T₂ = 273 K

∴ Using \(\frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2}\) we get,

⇒ \(V_2=\frac{p_1 V_1 T_2}{T_1 p_2}=\frac{10^{-4} \times 250 \times 273}{300 \times 76}=29.934 \times 10^{-5} \mathrm{~cm}^3\)

At STP, number of molecules in air of volume 22400 cm³ = 6 x 10²³.

So, that in volume 29.934 x 10^-5 cm³

= \(\frac{6 \times 10^{23}}{22400} \times 29.934 \times 10^{-5}=8.018 \times 10^{15}\)

Atmospheric Pressure And Air Density Relationship

Example 7. Two containers of volume 5 L and 3 L contain air at 3 standard atmospheres and 7 standard atmospheres respectively. The containers are now connected by a short narrow tube. What will be the common pressure in both containers?
Solution:

Given

Two containers of volume 5 L and 3 L contain air at 3 standard atmospheres and 7 standard atmospheres respectively. The containers are now connected by a short narrow tube.

Suppose the containers have n₁ and n₂ number of moles of the gas.

∴ 5×3 = n₁RT….(1)

and 3×7 = n₂RT…(2)

Therefore, 15 + 21 = (n₁ + n₂)RT [adding (1) and (2)]

or, (n₁ + n₂)RT= 36

At constant temperature, let the common pressure attained be p.

At that common pressure p, p(5 + 3) = (n₁ + n₂)RT = 36

∴ p = 36/8 = 4.5 standard atmospheres.

Example 8. Two bulbs of equal volume are connected by a narrow tube of negligible volume and filled with a gas at STP. If one of the bulbs is kept in melting ice and the other in a water bath at 62°C, what will be the new pressure of the gas?
Solution:

Given

Two bulbs of equal volume are connected by a narrow tube of negligible volume and filled with a gas at STP. If one of the bulbs is kept in melting ice and the other in a water bath at 62°C

Let volume of each bulb =Vcm³ and each contains n number of moles of the gas.

∴ Total number of moles contained in the bulb initially

= \(2 n=\frac{76 \times 2 V}{R \times 273} \quad[\text { from } p V=n R T]\)….(1)

Let the final pressure in both the bulbs = p.

Number of moles in one of the bulbs = \(\frac{p V}{R \times 273}\)

and that in the other bulb  = \(\frac{p V}{T(273+62)}=\frac{p V}{R \times 335}\)

∴ Total number of moles contained in the bulbs = \(\frac{p V}{R \times 273}+\frac{p V}{R \times 335}=\frac{p V}{R}\left(\frac{1}{273}+\frac{1}{335}\right)\)…(2)

From (1) and (2) we get, \(\frac{76 \times 2 V}{R \times 273}=\frac{p V}{R}\left[\frac{1}{273}+\frac{1}{335}\right]\)

or, \(\frac{p V}{R}(0.0037+0.0030)=\frac{76 \times V \times 2}{R \times 273}\)

or, \(p \times 0.0067=0.5568 or, p=\frac{0.5568}{0.0066}=83.10 \mathrm{cmHg}\).

Bulk Modulus And Relation Between Pressure And Density

Example 9. An air bubble rises from the bottom of a lake to its upper surface. The diameters of the bubble at the bottom and the surface are 3.6 mm and 4 mm respectively. Depth of the lake is 2.5 m and the temperature at the upper surface is 40°C. Find the temperature at the bottom of the lake. Ignore the change in density of water with height. (Atmospheric pressure = 76 cmHg and g = 980cm · s^-2)
Solution:

Given

An air bubble rises from the bottom of a lake to its upper surface. The diameters of the bubble at the bottom and the surface are 3.6 mm and 4 mm respectively. Depth of the lake is 2.5 m and the temperature at the upper surface is 40°C.

Pressure at the bottom of the lake p₁ =76x 13.6×980 + 250x 1×980

= (76 x 13.6 + 250) x 980 dyn · cm^-2

Volume of the air bubble at the bottom \(V_1=\frac{4}{3} \pi(0.18)^3 \mathrm{~cm}^3\)

Let the temperature at the bottom of the lake = T₁

Now, at the surface, pressure p₂ = 76 x 13.6 x 980 dyn · cm^-2

volume of the air bubble \(V_2=\frac{4}{3} \pi(0.2)^3 \mathrm{~cm}^3 \text {; }\); temperature T₂ = 273 + 40 = 313 K

Now using \(\frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2}\), we get

⇒ \(\frac{(76 \times 13.6+250) \times 980 \times \frac{4}{3} \pi(0.18)^3}{T_1 . \quad}=\frac{76 \times 13.6 \times 980 \times \frac{4}{3} \pi(0.2)^3}{313}\)

or, \(T_1=283.37 \mathrm{~K}=283.37-273^{\circ} \mathrm{C}=10.37^{\circ} \mathrm{C}\).

Example 10. A balloon at STP can lift a total mass of 175 kg attached with it When the barometer reads 50 cmHg and the temperature becomes -10°C at an upper point to where the balloon rises, find the maximum mass that can be lifted. Consider the volume of the balloon to be a constant.
Solution:

Given

A balloon at STP can lift a total mass of 175 kg attached with it When the barometer reads 50 cmHg and the temperature becomes -10°C at an upper point to where the balloon rises

The change in lifting capacity is due to the change in the upthrust, as the density of air changes at higher altitude due to the change in temperature and pressure.

Let V = volume of the balloon, ρ₁ = density at STR ρ₂ = density at 50 cmHg and -10°C; M = mass it can carry at the given altitude.

Hence, from Archimedes’ principle, \(V \rho_1=175 \mathrm{~kg} \text { and } V \rho_2=M \mathrm{~kg}\)

Now, \(\frac{p_1}{\rho_1 T_1}=\frac{p_2}{\rho_2 T_2} or, \frac{p_1}{V \rho_1 T_1}=\frac{p_2}{V \rho_2 T_2}\)

Substituting the corresponding values, we get, \(\frac{76}{175 \times 273}=\frac{50}{M \times 263}\)

or, M = \(\frac{175 \times 273 \times 50}{263 \times 76}=119.5 \mathrm{~kg}\).

Pressure Vs Density Graph Explanation

Example 11. A chamber contains a mass m₁ of a gas at pressure p₁. A second chamber contains a mass m₂ of the same gas at pressure p₂. If the two chambers are now connected, what will be the pressure of the gas mixture?
Solution:

Given

A chamber contains a mass m₁ of a gas at pressure p₁. A second chamber contains a mass m₂ of the same gas at pressure p₂. If the two chambers are now connected,

Let V₁ = volume of the 1st chamber, V₂ = volume of the 2nd chamber,

M = molecular weight of the gas, p = final pressure of the gas mixture,

T = constant temperature before and after mixing of the gases.

We use the relation \(p V=n R T=\frac{m}{M} R T\)

∴ For the 1st chamber, \(p_1 V_1=\frac{m_1}{M} R T\)

and for the 2nd chamber, \(p_2 V_2=\frac{m_2}{M} R T\)

∴ \(p_1 V_1+p_2 V_2=\left(m_1+m_2\right) \frac{R T}{M}\)

Using the relation for the gas mixture, we have \(p\left(V_1+V_2\right)=\left(m_1+m_2\right) \frac{R T}{M}\)

∴ \(p\left(V_1+V_2\right)=p_1 V_1+p_2 V_2 \text { or, } p=\frac{p_1 V_1+p_2 V_2}{V_1+V_2}\)

Now, \(V_1=\frac{m_1}{p_1} \frac{R T}{M} and V_2=\frac{m_2}{p_2} \frac{R T}{M}\).

So, \(V_1+V_2=\left(\frac{m_1}{p_1}+\frac{m_2}{p_2}\right) \frac{R T}{M}=\frac{p_2 m_1+p_1 m_2}{p_1 p_2} \frac{R T}{M}\)

∴ p = \(\left(m_1+m_2\right) \frac{R T}{M} \cdot \frac{p_1 p_2}{p_2 m_1+p_1 m_2} \cdot \frac{M}{R T}\)

= \(\frac{p_1 p_2\left(m_1+m_2\right)}{p_2 m_1+p_1 m_2} .\)

Example 12. A 100 cm long glass capillary tube, closed at both ends, has a mercury thread of length 10 cm. When the tube is horizontal, the mercury thread stays at the middle of the tube with air columns of equal length on either side, at 76 cmHg pressure and 27°C. Now, the temperature of one side is changed to 0°C, and of the other side to 127°C. Find the length and the pressure of the air column kept at 0°C. Neglect expansions of glass and mercury.
Solution:

Given

A 100 cm long glass capillary tube, closed at both ends, has a mercury thread of length 10 cm. When the tube is horizontal, the mercury thread stays at the middle of the tube with air columns of equal length on either side, at 76 cmHg pressure and 27°C. Now, the temperature of one side is changed to 0°C, and of the other side to 127°C.

Let the area of the cross-section of the capillary be α cm².

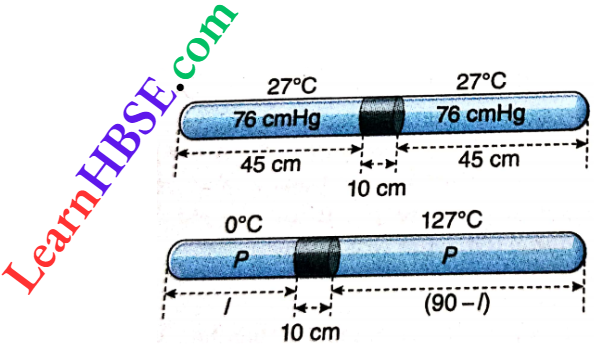
In the first case, the volume of air on either side of the mercury thread in the tube, V₁ = 45α cm³; temperature,

T₁ = 273 + 27 = 300 K; pressure of air, p₁ = 76 cmHg.

In the second case, let the left side of the Hg thread inside the tube be at 0°C or 273 K and the other side be at 127°C or 400 K.

Let the pressure of the confined air on each side = p cm.

Let l = length of the air column at 0°C; (90 -l) = length of the other air column at 127°C.

Using the equation of state, \(\frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2}, \frac{76 \times 45 \alpha}{300}=\frac{p l \alpha}{273}\)…(1)

and \(\frac{76 \times 45 \alpha}{300}=\frac{p(90-l) \alpha}{400}\)…(2)

From (1) and (2) we get, \(\frac{p \times l \times \alpha}{273}=\frac{p(90-l) \alpha}{400}\)

or, \(400 l=273(90-l) or, 673 l=273 \times 90\)

∴ l = \(\frac{90 \times 273}{673}=36.5 \mathrm{~cm} \text {. }\)

From equation (1), \(\frac{76 \times 45 \alpha}{300}=\frac{p \times 36.5 \alpha}{273} \text { or, } p=85.3 \mathrm{cmHg}\)

∴ The length of the air column at 0°C is 36.5 cm and its pressure is 85.3 cmHg.

Pressure And Density Formula In Fluid Mechanics

Example 13. Two heat proof containers of volumes IL and 3L are connected by a tube. Keeping the valve attached to the tube dosed, the 1st container is filled with nitrogen at 0°C and at 0.5 standard atmosphere pressure, and the 2nd container with argon at 100°C and at 1.5 standard atmosphere pressure. The temperature of the gas mixture becomes 79 °C when the valve is opened. Find the pressure of the gas mixture.
Solution:

Given

Two heat proof containers of volumes IL and 3L are connected by a tube. Keeping the valve attached to the tube dosed, the 1st container is filled with nitrogen at 0°C and at 0.5 standard atmosphere pressure, and the 2nd container with argon at 100°C and at 1.5 standard atmosphere pressure. The temperature of the gas mixture becomes 79 °C when the valve is opened.

In the 1st container, pressure of nitrogen (p₁) = 0.5 standard atmosphere, volume (V₁) = 1 L, temperature (T₁) = 0 + 273 = 273 K;

and in the 2nd container, pressure of argon (p₂) = 1.5 standard atmosphere, volume (V₂) = 3 L, temperature (T₂) = 100 + 273 = 373 K

When the valve is opened, let the pressure of the gas mixture be p volume, V = 4L and temperature, T = 273 + 79 = 352 K

As \(\frac{p V}{T}=n R\),

we have, \(n_1 R+n_2 R=\left(n_1+n_2\right) R\)

or, \(\frac{p_1 V_1}{T_1}+\frac{p_2 V_2}{T_2}=\frac{p V}{T}\)

or, \(\frac{0.5 \times 1}{273}+\frac{1.5 \times 3}{373}=\frac{p \times 4}{352} \)

or, \(\frac{p}{88}=0.0018+0.0120\)

∴ p =0.0138×88 = 1.2144 standard atmosphere.

Example 14. Two glass bulbs of volumes 3 L and 1 L are connected by a narrow tube. The system is filled with air at 30°C temperature and at 76 cmHg pressure. Now the bulb of volume 3 L is immersed in water vapour at temperature 100°C while the other bulb is kept at 30°C. Find the air pressures in the two bulbs. Neglect the volume expansion of the 3 L bulb.
Solution:

Given

Two glass bulbs of volumes 3 L and 1 L are connected by a narrow tube. The system is filled with air at 30°C temperature and at 76 cmHg pressure. Now the bulb of volume 3 L is immersed in water vapour at temperature 100°C while the other bulb is kept at 30°C.

Initially the total volume of the bulbs (V) = 3 + l= 4L,air pressure (p₁) = 76 cmHg, temperature of air (T₁) = 273 + 30 = 303 K

In the 2nd case, air pressure = p₂

temperature of 3 L bulb = 100 + 273 = 373 K

temperature of 1L bulb = 30 + 273 = 303 K

We use the relation, n = \(\frac{p V}{R T}\)

In the 1st case, number of gram-molecules in the gas

= \(\frac{76 \times 3}{R \times 303}+\frac{76 \times 1}{R \times 303}=\frac{76}{R \times 303}(3+1)=\frac{76 \times 4}{R \times 303}\)

Let in the 2nd case, air pressure = p

No. of gram-molecules = \(\frac{p \times 3}{R \times 373}+\frac{p \times 1}{R \times 303}=\frac{p}{R}\left(\frac{3}{373}+\frac{1}{303}\right)\)

∴ No. of gram-molecules is unchanged,

=  \(\frac{76 \times 4}{R \times 303}=\frac{p}{R}\left(\frac{3}{373}+\frac{1}{303}\right) \text { or, } \frac{76 \times 4}{303}=p\left(\frac{909+373}{373 \times 303}\right)\)

or, \(p=\frac{76 \times 4 \times 373}{1282}=88.4 \mathrm{cmHg} .\)

Derivation Of Pressure And Density Relation In Physics

Example 15. A narrow tube of uniform cross-section is closed at one end. Inside this tube a mercury thread of length hem detaches some air from the atmosphere outside. When the tube is held vertical keeping its closed end up, the length of the confined air column becomes l₁ cm. Again the length of the air column becomes l₂ cm when the tube is held vertical keeping its open end up. Find the magnitude of the atmospheric pressure.
Solution:

Given

A narrow tube of uniform cross-section is closed at one end. Inside this tube a mercury thread of length hem detaches some air from the atmosphere outside. When the tube is held vertical keeping its closed end up, the length of the confined air column becomes l₁ cm. Again the length of the air column becomes l₂ cm when the tube is held vertical keeping its open end up.

Let the atmospheric pressure =pcmHg; cross-section of the tube = α cm².

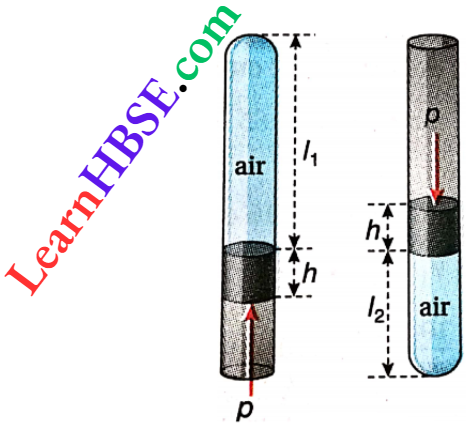
When the closed end of the tube is at the top, the volume of the confined air column V₁ = l₁αcm³;

pressure of confined air p₁ = (p- h) cmHg.

Now when the open end is at the top the volume of the confined air column V₂ = l₂ α cm³

pressure of confined air p₂ = (p + h) cmHg.

According to Boyle’s law p₁V₁ = p₂ V₂

or, \((p-h) l_1 \alpha=(p+h) l_2 \alpha\)

or, \((p-h) l_1=(p+h) l_2 or, p=\frac{l_1+l_2}{l_1-l_2} h\)

Hence, atmospheric pressure = \(\frac{l_1+l_2}{l_1-l_2}\) h cmHg.

Example 16. A glass tube of uniform area of cross-section and open at one end, encloses some air at 27°C by a 4 cm long mercury thread that acts like a piston. When the tube is held vertical with its open end up length of the air column in the tube is 9 cm. When the open end is held downwards by turning the tube, the length of the enclosed air column becomes 10 cm. Find

1. The value of the atmospheric pressure,
2. The temperature at which the length of the air column becomes 9 cm again, while the tube is still held inverted.

Solution:

Given

A glass tube of uniform area of cross-section and open at one end, encloses some air at 27°C by a 4 cm long mercury thread that acts like a piston. When the tube is held vertical with its open end up length of the air column in the tube is 9 cm. When the open end is held downwards by turning the tube, the length of the enclosed air column becomes 10 cm.

Let the atmospheric pressure = p cmHg, and the area of the cross-section of the tube = α cm².

When the open end is kept upwards, the volume of the confined air, V₁ = 9αcm³ and pressure p₁ = (p + 4)cmHg.

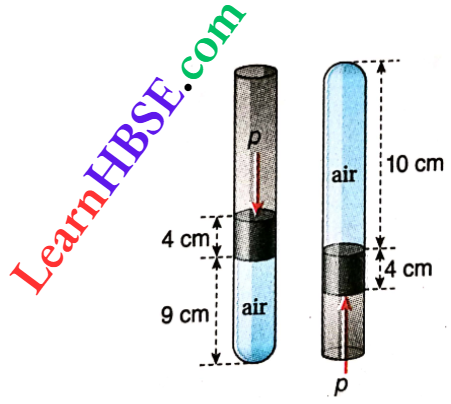
On inverting the tube, volume of the confined air V₂ = 10α cm³ and pressure p₂ =(p-4)cmHg.

Assuming temperature to be constant at 27°C, from Boyle’s law p₁V₁ = p₂V₂

or, 9α(p + 4) = 10α(p-4)

or, 9p + 36 = 10p-40, or, p= 76 cmHg

Suppose at T₂ K, the length of the air column becomes 9 cm again when the tube is still held inverted.

Then its pressure, p₂ = 76 – 4 = 72 cmHg and volume V₂ = 9αcm³.

∴ \(\frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2}\)

or, \(\frac{(76+4) \times 9 \alpha}{273+27}=\frac{72 \times 9 \alpha}{T_2} \quad \text { or, } \frac{80}{300}=\frac{72}{T_2}\)

∴ \(T_2=270 \mathrm{~K}=(270-273)^{\circ} \mathrm{C}=-3^{\circ} \mathrm{C}\)

Pressure Density Temperature Relation In Thermodynamics

Example 17. A uniform glass tube closed at both ends, encloses air columns of equal lengths on either side of a mercury thread of length 5 cm, when the tube is placed horizontally. The pressure of the enclosed air is p. When the tube is placed at 60° to the vertical, the upper and the lower columns of air are of lengths 46 cm and 44.5 cm respectively. Find the value of p. The Temperature of the system remains constant at 30°C.
Solution:

Given

A uniform glass tube closed at both ends, encloses air columns of equal lengths on either side of a mercury thread of length 5 cm, when the tube is placed horizontally. The pressure of the enclosed air is p. When the tube is placed at 60° to the vertical, the upper and the lower columns of air are of lengths 46 cm and 44.5 cm respectively.

Let in the first case, length of air column on each side of the mercury thread = l.

Again, length of the tube = 44.5 + 46 + 5 = 95.5 cm.

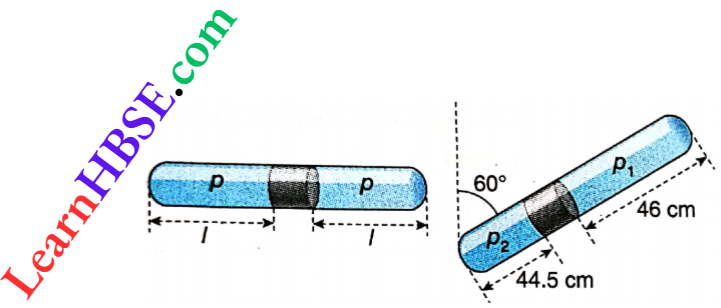
∴ \(l=\frac{95.5-5}{2}=45.25 \mathrm{~cm}\)

In the second case, p₂ = p₁ + 5cos60°

= p₁+ 2 = (p₁+ 2.5) cmHg

If in this case, V₁ and V₂ are the volumes of the upper and the lower air columns in the tube, then according to Boyle’s law,

p₁V₁ = p₂V₂

or, p₁ · 46α’ = (p₁ +2.5) x 44.5α

[where α = cross-sectional area of the tube]

Solving we get, p₁= 74.17 cm

Again, pV = p₁V₁

or, \(p=\frac{p_1 V_1}{V}=\frac{74.17 \times 46 \alpha}{45.25 \alpha}=75.4 \mathrm{~cm}\)

i.e., p = 75.4 cmHg

Hydrostatic Pressure And Density Formula

Example 18. The reading in a barometer changes from 75 cmHg to 25 cmHg when 10 cm³ of air at atmospheric pressure is introduced in the vacuum space of the barometer tube. What is the volume of air In the tube?
Solution:

Given

The reading in a barometer changes from 75 cmHg to 25 cmHg when 10 cm³ of air at atmospheric pressure is introduced in the vacuum space of the barometer tube.

Pressure of confined air =75-25 = 50 cmHg.

Initial volume of air V₁ = 10 cm³ and initial pressure p₁ = 75 cmHg.

Final volume of air = V₂ cm³ and final pressure p₂ = 50 cmHg.

Using Boyle’s law p₁V₁ = p₂V₂ we get,

⇒ \(V_2=\frac{p_1 V_1}{p_2}=\frac{75 \times 10}{50}=15\)

So, the volume occupied by the air inside the barometer is 15 cm³.

Example 19. The reading of a barometer decreases from 75 cmHg to 65 cmHg when some air is introduced in the vacuum space of the tube. The initial length of the space was 6 cm. If the area of the cross-section of the tube is 1 cm², what is the volume of this air at standard pressure?
Solution:

Given

The reading of a barometer decreases from 75 cmHg to 65 cmHg when some air is introduced in the vacuum space of the tube. The initial length of the space was 6 cm. If the area of the cross-section of the tube is 1 cm²

Standard pressure means p₁ = 76 cmHg.

The volume of air at that pressure = V₁ cm³.

Pressure of confined air p₂ = 75 – 65 = 10 cmHg.

Volume of confined air V₂ = {6+ (75-65)} x 1 = 16 cm³.

Using Boyle’s law, p₁V₁ = p₂V₂

or, \(V_1=\frac{p_2 V_2}{p_1}=\frac{10 \times 16}{76}=2.105\)

So the confined air occupies a volume of 2.105 cm³ at standard pressure.

Example 20. An air bubble of volume 20 cm³ forms in a lake at a depth of 40 m below the water surface. What will be its volume when it rises just below the water surface? (Standard atmospheric pressure = 76 cmHg)
Solution:

Given

An air bubble of volume 20 cm³ forms in a lake at a depth of 40 m below the water surface.

Volume of the air bubble at a depth of 40 cm, V₁ = 20 cm³.

Pressure on the bubble there, p₁ = atmospheric pressure + pressure due to 4000 cm of water column

= 76 x 13.6 x 980 + 4000 x 1 x 980

= (76 x 13.6 + 4000) x 980 dyn · cm^-2

Let the volume of the bubble just below die surface be V₂.

Pressure on the bubble just below the surface, p₂ = 76 x 13.6 x 980 dyn • cm²

From Boyle’s law, p₁V₁ = p₂V₂

or, 980 x (76 x 13.6 + 4000) x 20 = V₂ x 76 x 13.6 x 980

∴ \(V_2=\frac{(76 \times 13.6+4000) \times 20}{76 \times 13.6}=97.4 \mathrm{~cm}^3\)

Ideal Gas Law Relation Between Pressure And Density

Example 21. In a capillary tube, closed at one end, some air is enclosed by a mercury thread of length 10 cm. When the tube is kept horizontal the length of the air column is 17 cm. When it is held vertical with the open end up, the length changes to 15 cm. What will be the length of the air column when the tube is held vertical with the open end downwards?
Solution:

Given

In a capillary tube, closed at one end, some air is enclosed by a mercury thread of length 10 cm. When the tube is kept horizontal the length of the air column is 17 cm. When it is held vertical with the open end up, the length changes to 15 cm.

Let atmospheric pressure = pcmHg; crosssectional area of the tube = α cm².

When the tube is horizontal, pressure of the confined air, p₁ = p cmHg,

volume of this confined air, V₁ = 17 α cm_³.

When the tube is held vertical with the open end up, pressure of the confined air, p₂ = (p + 10) cmHg,

volume of this confined air, V₂ = 15α cm³

According to Boyle’s law, px 17α = (p + 10) x 15α or, p = 75

∴ Atmospheric pressure = 75 cmHg

Again, when the tube is held vertical with the open end downwards,

pressure of the confined air, p₃ = (p-10) cmHg,

volume of this confined air, V₃ = hα cm³

[where h = length of the air column]

According to Boyle’s law, \(p_1 V_1=p_3 V_3 \text { or, } p \times 17 \alpha=(p-10) \times h \alpha \)

or, h = \(\frac{17 p}{p-10}=\frac{17 \times 75}{65}=19.6 \mathrm{~cm}\).

Example 22. Volume of a room is 15 m x 12 m x 8 m. The room was at 22°C in the morning. What is the percentage of initial volume of air of the room that Is expelled when the room temperature reaches 30° C at noon? The pressure remains constant during die change of temperature.
Solution:

Given

Volume of a room is 15 m x 12 m x 8 m. The room was at 22°C in the morning.

From Charles’ law: \(\frac{V_1}{T_1}=\frac{V_2}{T_2}\) or, \(\frac{V_1}{V_2}=\frac{T_1}{T_2}\)

or, \(\frac{V_1}{V_2-V_1}=\frac{T_1}{T_2-T_1} or, \frac{V_2-V_1}{V_1} \times 100=\frac{T_2-T_1}{T_1} \times 100\)

Given, \(T_1=22^{\circ} \mathrm{C}=295 \mathrm{~K}, T_2=30^{\circ} \mathrm{C}=303 \mathrm{~K}, \quad V_2-V_1\) = volume of expelled air

∴ \(\frac{V_2-V_1}{V_1} \times 100=\frac{T_2-T_1}{T_1} \times 100=\frac{303-295}{295} \times 100=2.7\)

∴ 2.7% of air will be expelled from the room.

Example 23. Air is enclosed in a glass container at 67°C. Find the temperature to which the container is to be raised at constant pressure, so that 1/3 rd of the final volume of the air is expelled from the vessel? (Neglect the expansion of glass)
Solution:

Given

Air is enclosed in a glass container at 67°C.

Let initially the volume of air = V₁

In this case, temperature of air, T₁ = 273 + 67 = 340 K

Suppose the volume of the air becomes V₂ at a temperature T₂.

∴ Volume of expelled air = 1/3 V₂

∴ \(V_2=V_1+\frac{1}{3} V_2 \text { or, } V_2=\frac{3}{2} V_1\)

Since the pressure is constant, we can write \(\frac{V_1}{T_1}=\frac{V_2}{T_2}\)

∴ \(\frac{V_1}{340}=\frac{\frac{3}{2} V_1}{T_2}\)

or, \(T_2=\frac{3}{2} \times 340=510 \mathrm{~K}=(510-273)^{\circ} \mathrm{C}=237^{\circ} \mathrm{C} .\)

Thermodynamics – First And Second Law Of Thermodynamics The First Law Of Thermodynamics

The first law of thermodynamics is nothing but energy conservation applied to a thermodynamic system. From the equation W = JH, we know that an amount of work W is spent to produce an equivalent amount of heat H and from H amount of heat, an equivalent amount of work W is obtained.

Hence, heat and mechanical energy (work) are interconvertible. But in practice, when a system takes some amount of heat from its surroundings, it is used up in two ways:

1. A part of it increases the internal energy of the system and
2. The remaining part is converted into some external work done by the system, i.e., heat absorbed = rise in internal energy + external work done.

This is the first law of thermodynamics.

The first law of thermodynamics is, in essence, the energy conservation law which is applicable to every thermodynamic system together with its surroundings.

Let U_i = initial internal energy of a system,

Q = heat taken by the system from the surroundings,

U_f = final internal energy of the system,

W = external work done by the system.

Here, U_f– U_t = ΔU = change in internal energy. So the first law states that,

Q = \(\left(U_f-U_i\right)+W=\Delta \boldsymbol{U}+\boldsymbol{W}\)….(1)

First Law Of Thermodynamics Equation Class 11 HBSE

In this equation, W and Q are expressed in the same unit.

So Joule’s equivalent is J = 1.

When the internal energy of a system does not change, i.e., Uj-= Up we get, Q= W.

If, on the other hand, W is expressed in joule and Q in calorie, then J ≠ 1. We can then write, W= JQ. (the symbol H for heat is replaced by Q here).

So, Joule’s law of mechanical equivalent of heat is a special case of the first law of thermodynamics (where ΔU =0)

If a small amount of heat dQ changes the internal energy of a system by dU and an external work dW is done, then

dQ = dU + dW……(2)

This is the differential form of the first law of thermodynamics, whereas equation (1) is known as the integral form.

In equations (1) and (2), the convention is:

1. Q or dQ is considered positive when heat is absorbed by a system;
2. Q or dQ is considered negative when heat is released by a system.

First Law Of Thermodynamics Class 11 HBSE Notes

Significance of the first law of thermodynamics: From the first law of thermodynamics, it is known that mechanical energy can be converted into heat and vice versa. Certain amount of heat is required to do a certain amount of work. On the other hand, a certain amount of work has to be done to generate a certain amount of heat.

• The first law of thermodynamics indicates a new property of a body internal energy. In different thermodynamic processes, if we take only work and heat as the two manifestations of energy, the conservation of energy principle is violated.
• However, the body in every state has some internal energy. In every process, if we consider the change of this internal energy along with heat and work, energy remains conserved in all cases.
• This internal energy (U) is a state function. During the transformation from one state of a body to another, the change of internal energy does not depend on the intermediate path. In thermodynamics, there is no need to identify the source of internal energy.
• But it is seen from the kinetic theory of gases that, the kinetic energy and the potential energy due of to translational, rotational, and vibrational motions of the molecules of a body are the sources of its internal energy.

The perpetual motion of the first kind: it is impossible to get work without dissipation of energy. So, it is impossible to invent a machine that can work indefinitely without any supply of energy. If a machine can work indefinitely without any energy input, its motion is called the perpetual motion of the first kind.

But the first law of thermodynamics, which expresses the law of conservation of energy, states that this is impossible. So, perpetual motion of the first kind does not exist in nature.

Limitations Of First Law Of Thermodynamics Class 11 HBSE

Origin of internal energy: For complete conversion between W and Q, we have W = Q. Then from the first law, U_f – U_i = 0 or, U_f = U_i i.e., the internal energy of a system does not change.

• But complete conversion between W and Q is an ideal case, and has some natural restrictions. Thus, directly from the law of conservation of energy, we get the existence of a new thermodynamic property — the internal energy U of a system.
• For example, when a system takes some heat from outside but does no work (W = 0), we have Q = U_f– U_i, or heat absorbed = increase in internal energy.
• So, the effect of heat on a system, doing no work, is a change in its internal energy. These effects are rise in temperature, melting of a solid, vaporization of a liquid, etc. In each of these examples, the change in temperature of the system or the latent heat is directly related to the change in its internal energy.

When the motion of the molecules in a system is considered, we get a clear picture of the internal energy of a system. But thermodynamics does not discuss molecular motions that will be dealt with in kinetic theory.

First Law Of Thermodynamics Derivation Class 11 HBSE

Internal energy of a gas: Thermal condition of a fixed mass of gas is determined by three quantities temperature, pressure and volume. But internal energy of a gas does not depend on all of these three quantities. It depends only on its temperature in some cases.

• For example, there is no change in internal energy if the pressure or volume of a monatomic ideal gas of a particular mass changes at constant temperature. If we know the rise in temperature of this type of gas, we can determine the increase in internal energy.
• But the change in internal energy does not always depend on the change in temperature. If a gas undergoes a phase change, there is no change in temperature, but its- internal energy changes.

Statement Of First Law Of Thermodynamics Class 11 HBSE

Limitations of the first law of thermodynamics: This law expresses the law of energy conservation. That is, it says that energy cannot be created or destroyed it can only be converted from one form to another. But it cannot predict anything about the direction of natural processes. It fails to explain why

1. Heat can flow only from higher to lower temperature and never from lower to higher temperature
2. Some amount of work can entirely be converted into heat, but complete conversion of heat into work never occurs in nature.

So, the maximum heat or work available from a certain amount of work or heat, respectively, cannot be determined from the first law of thermodynamics. These limitations are overcome by the formulation of another law, the second law of thermodynamics.

First Law Of Thermodynamics And Internal Energy Class 11 HBSE

Thermodynamics – First And Second Law Of Thermodynamics The First Law Of Thermodynamics Numerical Examples

Example 1. An ideal monatomic gas goes through a cyclic process ABCDA, as shown. Find out the work done and heat supplied in this cyclic process.

Applications Of First Law Of Thermodynamics Class 11 HBSE

Solution:

Work done in the cycle ABCD = area of ABCD

= AB-BC = (2p-p)(2V-V) = pV

Here, the initial state A = the final state A.

So, the change in internal energy, U_f – U_i = U_A – U_A =0

Then, U_f– U_i = Q-W or, Q = (U_f – U_i) + W= 0 + pV = pV

∴ Heat supplied in the cyclic process = pV.

First Law Of Thermodynamics Formula Class 11 HBSE

Example 2. The volume of 1 g of water (1 cm³) becomes 1671 cm³ on being converted to steam at standard atmosphere pressure. Find out the work done and rise in internal energy. Given, the latent heat of vaporization of water = 540 cal · g^-1 the standard atmosphere pressure = 1.013 x 10⁵ N · m^-2.
Solution:

W = \(\int_{V_1}^{V_2} p d V=p \int_{V_1}^{V_2} d V=p\left(V_2-V_1\right)\)

Here, \(V_2-V_1=1671-1\)

= \(1670 \mathrm{~cm}^3\)

= \(1670 \times 10^{-6} \mathrm{~m}^3=1.67 \times 10^{-3} \mathrm{~m}^3\)

First Law Of Thermodynamics Numerical Problems Class 11 HBSE

∴ W = \(\left(1.013 \times 10^5\right) \times\left(1.67 \times 10^{-3}\right) \)

= 169.17 J

∴ \(U_2-U_1=Q-W=540 \times 4.2-169.17\)

(\(540 \mathrm{cal}=540 \times 4.21\))

= 2099 J.

Viscosity And Surface Tension Rate Of Flow Of A Liquid And Continuity

Rate of flow Of liquid definition: For streamline flow of a perfectly incompressible liquid, the amount of liquid flowing through any cross section of a tube in a given time interval remains constant.

• The rate of flow of a liquid through a tube means the volume of liquid flowing through any cross-section of the tube per second.
• Suppose a liquid flows through a tube of cross-sectional area a with a uniform velocity ν. The volume of liquid flowing through any cross-section of the tube per second is equal to the volume of a cylinder of length v and cross-sectional area α.

∴ Volume of liquid flowing per second = the rate of flow of the liquid = velocity of flow x area of cross section of the tube = νa

Therefore, the mass of liquid flowing per second = velocity of flow x area of cross-section of the tube x density of the liquid = ναρ [ρ = density of the liquid]

Continuity of flow definition: For a streamlined flow of a fluid (liquid or gas) through a tube, the mass of the fluid flowing per second through any cross-section of the tube remains constant. This is known as the continuity of flow.

Viscosity And Surface Tension Class 11 HBSE Notes

Definition Of Equation Of continuity: Let us consider two sections A and B of a tube having cross-sectional areas a₁ and a₂ respectively. The velocities of the fluid at sections A and B are ν₁ and ν₂, and its densities are ρ₁ and ρ₂ respectively.

The mass of fluid flowing through section A per second = \(v_1 \alpha_1 \rho_1\) and the mass of fluid flowing through section B per second = \(v_2 \alpha_2 \rho_2\)

For streamline flow, the fluid enters through section A and leaves through section B, and does not remain stored in the region between A and B, hence

⇒ \(v_1 \alpha_1 \rho_1\) = \(v_2 \alpha_2 \rho_2\) …..(1)

The product vαρ is the mass flow rate. If the fluid is incompressible (like a liquid), then its density is constant, and in that case ρ₁ = ρ₂.

∴ \(v_1 \alpha_1\) = \(v_2 \alpha_2\)…….(2)

or, να = constant …..(3)

Equations (2) and (3) are known as the equations of continuity of liquid flow.

∴ \(\nu \propto \frac{1}{\alpha},\) which means that the velocity of liquid flow through any cross-section of a tube is inversely proportional to its cross-sectional area.

The equations of continuity essentially express the law of conservation of mass.

Viscosity And Surface Tension Definition Class 11 Physics

Energy of Liquid in Streamline Flow: At any point inside a flowing liquid, there are three forms of energy

1. Kinetic energy,
2. Potential energy and
3. Energy due to pressure.

1. Kinetic energy: If mass m of a liquid flows with a velocity v, then the kinetic energy of that liquid = = \(\frac{1}{2} m v^2\).

Kinetic energy per unit mass = \(\frac{1}{2}v^2\)

Kinetic energy per unit volume = \(\frac{1}{2} \frac{m}{V} v^2\) [volume of the liquid]

= \(\frac{1}{2} \rho v^2\left[\rho=\frac{m}{V}=\text { density of the liquid }\right]\)

2. Potential energy: If mass m of a liquid is at a height h above the surface of the earth, then the potential energy of that liquid = mgh.

Potential energy per unit mass = gh

Potential energy per unit volume = \(\frac{m g h}{V}\) = ρgh.

3. Energy due to pressure: if a liquid is under the action of some applied pressure, then it acquires some energy and this energy is known as energy due to pressure. The liquid can perform work by expending this energy. Let some liquid of density ρ whose free surface is PQ be kept in a container.

Viscosity And Surface Tension Derivation Class 11 HBSE

A narrow side tube AB of cross sectional area α is attached near the bottom of the container. This tube is fitted with a piston P, which can move freely along the tube. If the pressure of the liquid at rest along the axis of the narrow tube is p, then the force acting on the piston = pα.

If the piston is slowly pushed inside the tube through a distance x, then work done = pαx. As a result, liquid of volume αx or mass αxρ enters the container. Since the piston is moved slowly, the liquid acquires negligible velocity and hence it will possess no kinetic energy.

So the work done pax remains stored as potential energy in mass αxρ of the liquid that has entered the container. This energy is called the energy due to pressure for the liquid.

The energy due to pressure per unit mass of the liquid = = \(\frac{p a x}{a x \rho}=\frac{p}{\rho} .\)

∴ The energy due to pressure per unit volume of the liquid = \(\frac{p a x}{a x}=p\).

Bernoulli’s Theorem: The Swiss mathematician Daniel Bernoulli established a law for the streamline flow of an ideal fluid (which is incompressible and non-viscous). This law is known as Bernoulli’s theorem. It is an important theorem in Hydrodynamics.

Statement Of the Bernoulli’s theorem: For a streamline flow of an ideal liquid, the sum of the potential energy, kinetic energy, and energy due to pressure per unit volume of the liquid always remains constant at every point on the I streamline.

If the kinetic energy per unit volume of the liquid = \(\frac{1}{2} \rho v^2\); potential energy = pgh and energy due to pressure = p, then

⇒ \(\frac{1}{2} \rho v^2+\rho g h+p\) = constant

or, \(\frac{1}{2} v^2+g h+\frac{p}{\rho}\) = constant …..(1)

This is the mathematical form of Bernoulli’s theorem. Dividing equation (1) by g, we get,

⇒ \(\frac{v^2}{2 g}+h+\frac{p}{\rho g}\) = constant……..(2)

This also is a form of Bernoulli’s theorem. Here, \(\frac{v^2}{2 g}\) is called the velocity head, h is the elevation head, and \(\frac{p}{\rho g}\) is the pressure head. Each of these heads has the dimension of length.

So, velocity head + elevation head + pressure head
= constant …..(3)

According to relation (3), Bernoulli’s theorem can also be stated as follows.

For a streamline flow of an ideal liquid, the sum of the velocity head, elevation head and pressure head always remains constant at any point in the liquid.

Bernoulli’s theorem is based on the law of conservation of energy for the streamline motion of an ideal fluid. The theorem states that energy remains conserved along any streamline.

When the flow of liquid is horizontal, the height of each point in the liquid is assumed to be the same, i.e., h = constant. We can rewrite equation (2) as,

⇒ \(\frac{v^2}{2 g}+\frac{p}{\rho g}=\) constant

or, \(p+\frac{1}{\mathrm{a}} \rho v^2\) = constant

Hence, in the horizontal flow of a liquid, the sum of pressure and kinetic energy per unit volume of the liquid at any point is constant. This implies that where the velocity of flow is high, the pressure is low and vice-versa.

Factors Affecting Viscosity And Surface Tension Class 11

Applications of Bernoulli’s theorem

1. Velocity of efflux of a liquid and Torricelli’s theorem: If a small hole is present on the wall of a deep container containing liquid, then the velocity with which the liquid comes out through that small hole is called the velocity of efflux of the liquid.

In Fig, a liquid kept in a large container is emerging with velocity ν through the small hole on the wall of the container. The height of the free surface of the liquid above the hole is h and the depth of the liquid below the hole is h₁.

The total depth of the liquid H = h+ h₁. Let us consider a point B just outside the hole and another point A on the surface of the liquid. Atmospheric pressure p acts on A and B.

If the container is large and the hole is very small, then the free surface of the liquid will come down so slowly that the velocity of the free surface of the liquid would seem to be almost zero.

If we imagine a tube of flow starting from the free surface of the liquid and ending at the point B and apply Bernoulli’s theorem in that tube of flow, then

⇒ \(0+H+\frac{p}{\rho g}=\frac{v^2}{2 g}+h_1+\frac{p}{\rho g}\)

or,\(\frac{v^2}{2 g}=H-h_1=h\)

or, \(v^2=2 g h\)

or, \(v=\sqrt{2 g h}\)

• This is the velocity of efflux of a liquid through a small hole and it is known as Torricelli’s formula. According to this formula, the velocity of efflux of a liquid is the same as that of a body falling freely under gravity through a height h. So, Torricelli’s theorem can be stated as follows:
• The velocity of efflux of a1 liquid through any small hole or orifice is equal to that acquired by a body falling freely from rest under gravity from the free surface of the liquid to the level of the small hole.
• It should be mentioned that this ideal velocity cannot be attained by any liquid in reality because no liquid is non- viscous. It should be remembered that in Bernoulli’s theorem the effect of viscosity of the liquid has been neglected.

Difference Between Viscosity And Surface Tension Class 11

Horizontal range: Let, the first drop of liquid emerged from the orifice touches the ground at a distance x after time t. That means, the vertical displacement of the liquid drop is h₁.

Now, considering the motion of the liquid along the vertical direction,

initial velocity = 0, acceleration = g

From the equation h = ut+1/2gt² we get, h = 0 + 1/2gt²

∴ t = \(\sqrt{\frac{2 h_1}{g}}\)

Again, considering the motion of the liquid aong the horizontal direction, the initial velocity, ν = √2gh, acceleration = 0, time = t.

∴ Horizontal range, \(x=v t=\sqrt{2 g h} \times \sqrt{\frac{2 h_1}{g}}=2 \sqrt{h h_1}\)

2. Venturimeter: A venturimeter is used to measure the rate of flow of liquid through a tube. Its working principle is based on Bernoulli’s theorem.

• Shows the action of a venturimeter. The two ends of this tube are equally wide and the middle portion is narrow. Liquid flows through this tube in streamlines. The tube is kept horizontal.
• When a liquid flows through a venturimeter, the velocity of the liquid increases at the narrow part of the tube with consequent decrease in pressure. This decrease in pressure is measured with the help of two vertical tubes attached at the wide and the narrow parts of the venturimeter.

Let the velocity of the liquid at the wider part of the tube be ν₁ and the pressure be p₁ At the narrower part of the tube, the velocity of the liquid is ν₁ and the pressure is p₂.

According to Bernoulli’s theorem, \(\frac{v_1^2}{2 g}+\frac{p_1}{\rho g}=\frac{v_2^2}{2 g}+\frac{p_2}{\rho g}\)

the elevation head, h₁=h₂ since the tube is horizontal.

∴ \(\frac{p_1-p_2}{\rho g}=\frac{1}{2 g}\left(v_2^2-v_1^2\right) \text { or, } p_1-p_2=\frac{\rho}{2}\left(v_2^2-v_1^2\right)\)

or, \(h \rho g=\frac{\rho}{2}\left(v_2^2-v_1^2\right)\)

[h = difference in liquid levels in the vertical tubes attached to the venturimeter]

∴ h = \(\frac{1}{2 g}\left(v_2^2-v_1^2\right)\)

If the cross-sectional areas of the wide and the narrow parts of the venturimeter are α₁ and α₂ respectively, then according to the equation of continuity, we get,

⇒ \(\alpha_1 v_1=\alpha_2 v_2 \text { or, } \frac{v_1}{v_2}=\frac{\alpha_2}{\alpha_1}\)

∴ h = \(\frac{v_2^2}{2 g}\left(1-\frac{v_1^2}{v_2^2}\right)=\frac{v_2^2}{2 g}\left(1-\frac{\alpha_2^2}{\alpha_1^2}\right)\)

or, \(v_2^2=2 g h \cdot \frac{\alpha_1^2}{\alpha_1^2-\alpha_2^2}\)

or, \(v_2=\frac{\alpha_1}{\sqrt{\alpha_1^2-\alpha_2^2}} \cdot \sqrt{2 g h}\) …..(1)

Therefore, the volume of liquid flowing out per second,

V = \(\alpha_2 v_2=\frac{\alpha_1 \alpha_2 \sqrt{2 g h}}{\sqrt{\alpha_1^2-\alpha_2^2}}=\alpha_1 \alpha_2 \sqrt{\frac{2 g h}{\alpha_1^2-\alpha_2^2}}\)…….(2)

So, when α₁ and α₂ are known, by measuring h we can determine the rate of flow of the liquid through the tube with the help of equation (2).

Viscosity And Surface Tension Formula Class 11 HBSE

3. Pitot tube: A pitot tube is also used to measure the rate of flow of liquids. Its working principle is similar to that of a venturimeter. Its action also depends on Bernoulli’s theorem.

• In this instrument, two tubes AB and CED, open at both ends are introduced vertically and side by side inside the liquid. The open end B of the tube AB remains parallel to the flow of the liquid. The DE part of the tube CED is so bent that the opening D faces the flowing liquid normally.
• The height of the liquid column in the tube AB expresses the pressure of the liquid at the point B. Since the liquid flow is obstructed at the portion DE of the tube CED, the velocity of flow at point D is zero.

The difference in the liquid levels in the two tubes = h.

Let the velocity of liquid flow be ν.

The points B and D lie on the same horizontal plane; therefore, according to Bernoulli’s theorem,

⇒ \(\frac{1}{2 g} v^2+\frac{p_B}{\rho g}=0+\frac{p_D}{\rho g}\) [ρ= density of the liquid]

or, \(\frac{1}{2 g} v^2=\frac{p_D-p_B}{\rho g}\)

or, \(\frac{1}{2} v^2=\frac{h \rho g}{\rho} v^2=2 g h or, v=\sqrt{2 g h}\)

If the cross-section of the pipe where the two tubes are placed is a, then the volume of liquid flowing per second through that section, V = \(\alpha v=\alpha \sqrt{2 g h} .\)

When an aeroplane is in motion, the velocity of air currents can be determined with the help of a pitot tube.

4. Sprayer or atomizer: A sprayer or atomizer is used for spraying water, insecticides, etc. Its action also depends on Bernoulli’s theorem.

• The liquid to be sprayed is kept in a container A and its mouth is closed with the help of a cork or cap. A narrow tube B passes through the cap of the container. C is another tube through which air is blown. The tube C has a narrow tip.
• When air comes out from this narrow tip O with a high velocity, pressure at O decreases. Since O lies just above the open end of the tube B, the liquid rises through the tube B due to this low pressure, and as it meets the high-velocity air coming out of the tube C, it sprays out in the form of fine droplets.

Explanation of Some Phenomena with Bernoulli’s Theorem

1. It is not safe to stand near a fast-moving train: Due to the very high speed of the train, the air near the train also flows at a very high speed. As a result, pressure in that region decreases compared to the air pressure of the surrounding region. This excess surrounding pressure behind a person pushes him towards the train and may cause a serious accident.

2. The tin roof of a house is sometimes blown off during a storm: Since the velocity of the wind above the roof is very high, pressure becomes very low. The air inside the room is still and so the higher pressure from inside pushes the roof upwards and hence the roof may be lifted and blown off with the wind.

3. Two boats or ships moving side by side have a tendency to come closer: The speed of water in the narrow gap between boats or ships is greater than the speed of water on the other sides of the vessels. So, the pressure in that narrow region decreases. As a result, due to higher water pressure on the other sides of the boats or ships, they experience a lateral force and, hence, come closer.

4. Flying in air of typical-shaped objects: Let us take an object moving through air towards right.

• Its lower surface is flat, but the upper surface is oval-shaped. The relative motions of the streamlines of air moving above and below it are shown by arrows.
• Clearly, the upper streamline traverses a greater distance in any fixed interval of time; so its velocity is higher. Then, according to Bernoulli’s theorem, the air pressure above the object is less than that below it.
• As a result, a net upward pressure acts on the object. This helps the object to fly through air, provided its weight is sufficiently low. This is one of the principles utilised to fly an aeroplane.

Experiment On Viscosity And Surface Tension Class 11 HBSE

5. Magnus effect: When a spinning ball is thrown horizontally with a large velocity, it deviates from its usual parabolic path of spin free motion. This deviation can be explained on the basis of Bernoulli’s principle.

• When a ball moves forward, the air ahead the ball, moving with velocity v (say), rushes to fill up the vacant space behind the ball left evacuated by the motion of the ball.
• As the ball spins, the layer of air surrounding the ball also moves with the ball at a velocity u (say). From the fig, it can be stated that the resultant velocity of air above the ball becomes (v+ u) while that below that ball is (v- u).
• This difference in the velocities of air results in the pressure difference between the lower and upper faces of the ball. This pressure difference exerts a net upward force on the ball due to which it moves along a curved path as shown in Fig.
• If the spin of the ball is opposite to that shown in the Fig. a net downward force will act on it, deviating it from its original path. This effect is known as Magnus effect. If the surface of the ball is rough, more air is dragged and the path of the ball becomes more curved.

6. Blood flow and heart attack: An artery may get constricted due to the accumulation of plaque on its inner walls. In order to drive blood through this constriction the speed of the flow of blood is increased.

• This increased velocity lowers the blood pressure in the constricted region and the artery may collapse due to the external pressure.
• As a result, the heart exerts more pressure to open this artery and forces the blood through. As the blood rushes through the opening, the internal pressure once again drops due to some reasons leading to a repeat collapse which results in heart attack.

Rate Of Flow Of A Liquid Numerical Examples

Example 1. The pressure at an orifice situated at the lower side of a vessel filled with a liquid is greater than the atmospheric pressure by 9.8 x 10³ N · m^-2. What is the velocity of efflux if the density of the liquid is 2500 kg · m^-3? [g = 9.8 m · s^-2]
Solution:

Given

The pressure at an orifice situated at the lower side of a vessel filled with a liquid is greater than the atmospheric pressure by 9.8 x 10³ N · m^-2.

Velocity of efflux of the liquid, v = √2gh

According to the problem, hρg = 9.8 x 10³

or, \(g h=\frac{9.8 \times 10^3}{2500}\)

∴ v = \(\sqrt{\frac{2 \times 9.8 \times 10^3}{2500}}=2.8 \mathrm{~m} \cdot \mathrm{s}^{-1} .\)

Numerical Problems On Viscosity And Surface Tension Class 11

Example 2. Water is flowing through a horizontal tube of unequal cross-section. At a point where the velocity of water is 0.4 m · s^-1, the pressure is 0.1 m Hg. What is the pressure at a point where the velocity of water is 0.8 m · s^-1? The density of mercury = 13.6 x 10³ kg · m^-3.
Solution:

Given

Water is flowing through a horizontal tube of unequal cross-section. At a point where the velocity of water is 0.4 m · s^-1, the pressure is 0.1 m Hg.

According to Bernoulli’s theorem,

⇒ \(\frac{1}{2} v_1^2+\frac{p_1}{\rho}=\frac{1}{2} v_2^2+\frac{p_2}{\rho}\) (since the tube is horizontal)

or, \(p_2=p_1+\frac{1}{2} \rho\left(v_1^2-v_2^2\right)= 0.1 \times\left(13.6 \times 10^3\right) \times 9.8\) + \(\frac{1}{2} \times 10^3 \times\left\{(0.4)^2-(0.8)^2\right\}\)

= \(13088 \mathrm{~Pa}=\frac{13088}{\left(13.6 \times 10^3\right) \times 9.8} \mathrm{~m} \mathrm{Hg}\)

= 0.0982 m Hg

Example 3. A pitot tube is connected to a main pipeline of diameter 16 cm. The difference in height of the water columns in the two arms of the tube is 10 cm. Determine the rate of flow of water through the main pipe.
Solution:

Given

A pitot tube is connected to a main pipeline of diameter 16 cm. The difference in height of the water columns in the two arms of the tube is 10 cm.

Volume of water flowing through the pipe per second,

V = αv [v = velocity of water]

V = \(\alpha \sqrt{2 g h} \text { (Here, } \alpha=\pi(8)^2=64 \pi \mathrm{cm}^2, h=10 \mathrm{~cm} \text { ) }\)

∴ V = \(64 \pi \sqrt{2 \times 980 \times 10}=64 \pi \times 140\)

= 2.8 x 10⁴ cm³ = 0.028 m³.

Example 4. A venturimeter has been connected between two points of a pipe. The radii of the pipe at these two points are 5 cm and 3 cm respectively. The difference in pressure between these points is equal to that of a water column of height 5 cm. Determine the rate of flow of water through the pipe.
Solution:

Given

A venturimeter has been connected between two points of a pipe. The radii of the pipe at these two points are 5 cm and 3 cm respectively. The difference in pressure between these points is equal to that of a water column of height 5 cm.

The rate of flow of water,

V = \(\alpha_1 \alpha_2 \sqrt{\frac{2 g h}{\alpha_1^2-\alpha_2^2}}\)

[Here, \(\alpha_1=\pi(5)^2=25 \pi \mathrm{cm}^2, \quad \alpha_2=\pi(3)^2=9 \pi \mathrm{cm}^2\), h=5 \(\mathrm{~cm}, g=980 \mathrm{~cm} \cdot \mathrm{s}^{-2}\)]

= \(25 \pi \cdot 9 \pi \sqrt{\frac{2 \times 980 \times 5}{(25 \pi)^2-(9 \pi)^2}} \approx 3000.6 \mathrm{~cm}^3 \cdot \mathrm{s}^{-1} .\)

Example 5. Water from a tap falls vertically with a velocity of 3 m · s^-1. The area of the cross-section of the mouth of the tap is 2.5 cm². If the flow of water is uniform and steady throughout, then determine the cross-sectional area of the tube of flow of water at a depth of 0.8 m from the mouth of the tap. [g = 10 m · s^-2]
Solution:

Given

Water from a tap falls vertically with a velocity of 3 m · s^-1. The area of the cross-section of the mouth of the tap is 2.5 cm². If the flow of water is uniform and steady throughout

The area of cross-section of the mouth of the tap, A₁ = 2.5 cm², and velocity of water flow there, v₁ = 3 m · s^-1.

Let the area of cross-section of the tube of flow of water at a depth of 0.8 m below the tap be A₂ and the velocity of water flow there be v₂

∴ \(v_2^2=v_1^2+2 g hp\)

= (3)² + 2 x 10 x 0.8

= 9 + 16 = 25

or, v₂ = 5 m · s^-1

We know that, A₁ V₁ = A₂ V₂

or, \(A_2=\frac{A_1 v_1}{v_2}=\frac{2.5 \times 3}{5}=1.5 \mathrm{~cm}^2 .\)

Applications Of Viscosity And Surface Tension Class 11

Example 6. Water flows in streamline motion through a vertical tube of non-uniform cross-section. The radius of the tube at point P and at point Q are 1 cm and  0. 5 cm respectively. Point Q is at a distance of 40 cm from point P. The pressure difference between these points is 39.3 cm of water. Determine the rate of flow of water through the tube.

Solution:

Given

Water flows in streamline motion through a vertical tube of non-uniform cross-section. The radius of the tube at point P and at point Q are 1 cm and  0. 5 cm respectively. Point Q is at a distance of 40 cm from point P. The pressure difference between these points is 39.3 cm of water.

Accoring to the equation of continuity,

⇒ \(A_1 v_1=A_2 v_2\)

∴ \(v_2^2=\frac{A_1^2}{A_2^2} v_1^2\)

According to Bernoulli’s theorem,

⇒ \(\frac{v_1^2}{2 g}+h_1+\frac{p_1}{\rho g}=\frac{v_2^2}{2 g}+h_2+\frac{p_2}{\rho g}\)

or, \(\frac{v_2^2-v_1^2}{2 g}=\left(h_1-h_2\right)+\left(\frac{p_1-p_2}{\rho g}\right)\)

or, \(\frac{v_2^2-v_1^2}{2 g}=40+39.3 \frac{\rho g}{\rho g}=79.3 \mathrm{~cm}\)

∴ \(\frac{v_1^2}{2 g}\left[\frac{A_1^2}{A_2^2}-1\right]=79.3\)

or, \(\frac{v_1^2}{2 g}\left[\frac{(\pi)^2}{(0.25 \pi)^2}-1\right]=79.3\)

or, \(v_1=101.79 \mathrm{~cm} / \mathrm{s}\)

The rate of flow of water = \(A_1 v_1=101.79 \times \pi\)

=319.78 cm³

Example 7. A liquid of density 1000 kg/m³ is flowing in streamline motion through a tube of the non-uniform cross-section. The tube is inclined with the ground, The area of cross sections at points P and Q of the tube are 5 x 10^-3 m² and 10 x 10^-3 m² respectively. The height of the points P and Q from the ground are 3 m and 6 m respectively. The velocity of the liquid at point P is 1 m/s. Calculate the work done per unit volume due to

1. the pressure and
2. gravitational force for the flow of liquid from point P to point Q.

Solution: From equation  of continuity, \(A_1 v_1=A_2 v_2\)

or, \(v_2=\left(\frac{A_1}{A_2}\right) v_1=\left(\frac{5 \times 10^{-3}}{10 \times 10^{-3}}\right) \cdot(1)=\frac{1}{2} \mathrm{~m} / \mathrm{s}\)

Applying Bernoulli’s theorem we get,

⇒ \(p_1+\frac{1}{2} \rho v_1^2+\rho g h_1=\rho_2+\frac{1}{2} \rho v_2^2+\rho g h_2\)

or, \(\rho_1-\rho_2=\rho g\left(h_2-h_1\right)+\frac{1}{2} \rho\left(v_2^2-v_1^2\right)\)……….(1)

1. Work done per unit volume of the liquid due to the pressure of the streamline flow from P to Q is,

⇒ \(W_p =p_1-p_2\)

⇒ \(W_p =\rho g\left(h_2-h_1\right)+\frac{1}{2} \rho\left(\nu_2^2-v_1^2\right)[\text { from equation (1)] }\)

= \(\left[(1000)(9.8)(6-3)+\frac{1}{2}(1000)\left(\frac{1}{4}-1\right)\right]\)

= \(\left[3 \times 9.8-\frac{3}{8}\right] \times 10^3=29025 \mathrm{~J} / \mathrm{m}^3\)

2. Work done due to gravitational force for the streamline motion from P to Q is,

W_g = ρg(h₁ – h₂) = 1000 x 9.8 x (3 – 6)

= -29400 J/m³

Example 8. A big container is kept on a horizontal surface of uniform area of cross-section, A. Two non-viscous liquids of densities d and 2d which are not mixed with each other and not compressed, are kept in the container. The height of both liquid column is H/2 and the atmospheric pressure on the open surface of the liquid is p₀. A small orifice is created at a height h from the bottom of the container,

1. Calculate the initial velocity of efflux of the liquid through the orifice,
2. Calculate the horizontal distance x at which the first liquid drop emerged from the orifice will reach,
3. What will be the value of h if the value of the horizontal distance x to be maximum x_m? Also, calculate the value of x_m neglecting the air resistance.

Solution:

1. Let, the initial velocity of efflux of the liquid = v.

According to Bernoulli’s theorem,

⇒ \(p_0+d g\left(\frac{H}{2}\right)+2 d g\left(\frac{H}{2}-h\right)=p_0+\frac{1}{2}(2 d) v^2\)

or, \(v^2=\left(\frac{H}{2}+\frac{2 H}{2}-2 h\right) g or, v=\sqrt{(3 H-4 h)_2^g}\)

2. The time required to reach the ground of the first liquid drop emerged from the orifice is,

t = \(\sqrt{\frac{2 h}{g}}\)

∴ The horizontal distance traversed by the liquid is,

x = vt = \(\sqrt{(3 H-4 h)_2^g} \sqrt{\frac{2 h}{g}}\)

= \(\sqrt{h(3 H-4 h)}\)

3. The condition for x to be maximum (x_m):

x = \(\sqrt{h(3 H-4 h)}=\sqrt{-\left(4 h^2-3 h H\right)}\)

= \(\sqrt{\left\{(2 h)^2-2 \cdot 2 h \cdot \frac{3}{4} H+\left(\frac{3}{4} H\right)^2-\left(\frac{3}{4} H\right)^2\right\}}\)

= \(\sqrt{\frac{9}{8} H^2-\left(2 h-\frac{3}{4} H\right)^2}\)

∴ x = \(x_m \text { when } 2 h-\frac{3}{4} H=0\)

Hence, h= \(\frac{3}{8}H\)

∴ \(x_m=\sqrt{\frac{9}{8} H^2}=\frac{3}{2 \sqrt{2}} H\)