Vertical Circular Motion Class 11 Notes

Work And Energy – Rotational Motion Of A Body In A Vertical Circle

Non-uniform circular motion: When a body of mass m is tied to a string and is rotated in a vertical circle, it will not rotate with uniform speed in that circular path. So, it is an example of a non-uniform circular motion.

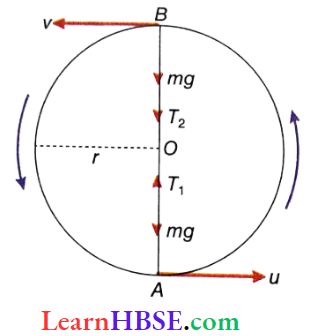
The magnitude of its velocity increases when it descends from the highest point B of the circle to the lowest point A. Again, the magnitude of velocity gradually decreases when it rises up to the highest point from the lowest point of the circle.

During its rotation, the weight of the body always acts vertically downwards, but the direction of centripetal force changes continuously. Hence, the tension in the string does not remain constant.

At the highest point B of the circular path, tension in the string and the weight of the body together provide the necessary centripetal force for the rotation of the body. If the velocity of the body is v and the tension in the string is T₂ at point B, then \(T_2+m g=\frac{m v^2}{r}\)

or, \(T_2=\frac{m v^2}{r}-m g\)…(1)

Again, the tension in the string at the lowest point A on the circular path acts in the vertically upward direction, i.e., towards the center of the circle, but the weight of the body acts vertically downwards.

Applications Of Vertical Circular Motion In Physics

As a result, the difference between the tension in the string and the weight of the body provides the necessary centripetal force. If the velocity of the body is u and the tension in the string is T₁ at point A, then

⇒ \(T_1-m g=\frac{m u^2}{r}\)

or, \(T_1=\frac{m u^2}{r}+m g\)…(2)

If the tension in the string at the point B is zero, i.e., if T₂ = 0, then

⇒ \(\frac{m v^2}{r}-m g=0 \quad \text { or, } \frac{m v^2}{r}=m g\)

or, v = \(\sqrt{r g}\)…(3)

Hence, if the value of v is less than \(\sqrt{r g}\) at the highest point, then the tension in the string becomes negative, i.e., the string gets relaxed. As a result, the body descends in a parabolic path instead of rotating along a circular path.

Hence, the least velocity of the body at the highest point on the circular path to maintain the vertical circular motion should be \(\sqrt{r g}\). This least velocity is called the critical velocity.

Vertical Circular Motion Class 11 Physics Notes

Least Velocity At The Lowest Point On The Circular Path Necessary To Maintain The Critical Velocity: If the potential energies of the body at points A and B are V₁ and V₂, respectively, then

total energy at point A = \(\frac{1}{2} m u^2+V_1 \text {. }\)

Similarly, total energy at point B = \(\frac{1}{2} m v^2+V_2 \text {. }\)

According to the principle of conservation of energy, \(\frac{1}{2} m u^2+V_1=\frac{1}{2} m v^2+V_2\)

or, \(V_2-V_1=\frac{1}{2} m\left(u^2-v^2\right)\)…(4)

When a body of mass m attains a height h, the potential energy gained by it = mgh. In the given figure, the height of the point B with respect to the point A is 2r.

So, the change in potential energy = V₂ – V₁ = mg · 2r

∴ From equation (4) we get, mg \(\cdot 2 r=\frac{1}{2} m\left(u^2-v^2\right)\)

or, \(4 g r=u^2-v^2\)

or, \(u^2=4 g r+v^2=4 g r+g r\)

(the least velocity at \(B, v=\sqrt{g r}\))

or, \(u^2=5 g r\)

or, \(u=\sqrt{5 g r}\)…(5)

Energy Conservation In Vertical Circular Motion Class 11

For rotation in a vertical circle, this is the least value of u. It should be noted that the value of this least velocity is independent of the mass of the body.

For this last value of u, the minimum value of tension at point A can be determined from equation (2).

⇒ \(\left(T_1\right)_{\min }=\frac{m u_{\min }^2}{r}+m g=\frac{m \cdot 5 g r}{r}+m g \)

= \(5 m g+m g=6 \mathrm{mg}\)

or, \(\left(T_1\right)_{\min }=6 \times\) weight of the body…(6)

So, if a body is rotated in a vertical circle, then at the lowest point of the circle, the minimum tension in the string is 6 times the weight of the body.

Vertical Circular Motion Formula Class 11

Rotation Of A Bucket Full Of Water In A Vertical Circle: When a bucket full of water is made to rotate with high speed in a vertical circle, it is seen that at the highest point of the circular path, though the bucket is inverted, water from it does not spill out. It is clear that when the bucket is at the highest position, two forces act simultaneously on the water in the bucket:

1. Downward weight (mg) of water (m = mass of water).
2. The upward reaction of the centripetal force; if the velocity of the bucket at the highest position is v and the radius of the circular path is r, the value of this centripetal force acting on the bucket due to its rotation = \(\frac{m v^2}{r}.\)

Thus, when the upward force becomes greater than the force downward, water in the bucket cannot fall down. So, the condition for water to not fall down is, \(\frac{m v^2}{r}.\) ≥ mg or, v² ≥ rg.

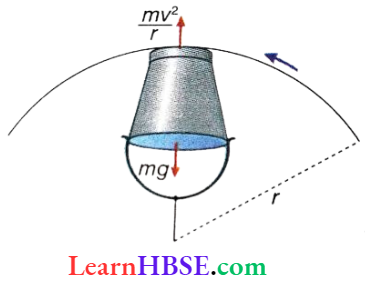
Hence, the minimum value of v should be \(\sqrt{r g}\).

According to equation (6), when this bucket is rotated along a complete circular path, at the lowest position of the bucket, the tension acting on the hand will be 6 times the weight of the bucket filled completely with water. Hence, it is difficult to perform the experiment with a heavy bucket full of water. However, it is easier with a bucket or some other container containing a small amount of water.

Work And Energy – Rotational Motion Of A Body In A Vertical Circle Numerical examples

Example 1. A body of mass 1 kg is tied with a thread and is whirled in a vertical circle of radius 50 cm with a speed of 500 cm · s^-1. What will be the tension in, the thread at the highest and the lowest positions of the body?
Solution:

Given

A body of mass 1 kg is tied with a thread and is whirled in a vertical circle of radius 50 cm with a speed of 500 cm · s^-1

Speed of the body at every point on the circular path is the same and its value, v = 500 cm · s^-1 = 5 m · s^-1.

So, at every point on the circular path, centripetal force, F = \(\frac{m v^2}{r}=\frac{1 \times(5)^2}{0.5}=50 \mathrm{~N}\)

Weight of the body = mg = 1 x 9.8 = 9.8 N

At the highest position, the tension in the thread (T₁) and the weight of the body both act downwards and together they provide the necessary centripetal force.

Hence, F = mg+ T₁ or, T₁ = F- mg = 50 – 9.8 = 40.2 N

At the lowest position, the tension in the thread (T₂) acts in the upward direction but the weight acts downwards, and hence, in this case, (T₂ – mg) provides the necessary centripetal force.

So, T₂ – mg – F or, T₂ = F+ mg = 50 + 9.8 = 59.8 N.

Minimum Velocity For Vertical Circular Motion Class 11

Example 2. A particle of mass 100 g is suspended from the end of a weightless string of length 100 cm and is rotated in a vertical plane. The speed of the particle is 200 cm · s^-1 when the string makes an angle of θ = 60° with the vertical. Determine

1. The tension in the string when θ = 60° and
2. The speed of the particle at the lowest position. Acceleration due to gravity = 980 cm · s^-2.

Solution:

Given

A particle of mass 100 g is suspended from the end of a weightless string of length 100 cm and is rotated in a vertical plane. The speed of the particle is 200 cm · s^-1 when the string makes an angle of θ = 60° with the vertical.

1. The body is rotated in a vertical plane.

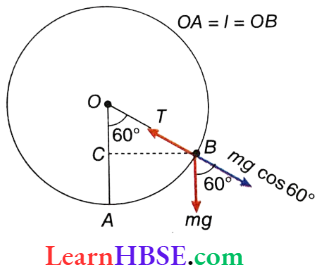
At point B, when the string makes an angle of 60° with the vertical, the velocity of the particle is v (say).

If the tension in the string is T, then T – \(mg \cos 60^{\circ}=\frac{m v^2}{r}\)

∴ T = \(m g \cos 60^{\circ}+\frac{m v^2}{r}\)

Here, v = \(200 \mathrm{~cm} \cdot \mathrm{s}^{-1} ; r=100 \mathrm{~cm} ; m=100 \mathrm{~g}\)

Real Life Examples Of Vertical Circular Motion Class 11

∴ T = \(100 \times 980 \times \frac{1}{2}+\frac{100 \times(200)^2}{100}\)

= \(8.9 \times 10^4 \mathrm{dyn} .\)

2. From the principle of conservation of energy we get, the kinetic energy of the body at the lowest point A = sum of the potential and kinetic energies at the point B

or, \(\frac{1}{2} m v_A^2=\frac{1}{2} m \nu^2+m g \cdot A C\)

(\(v_A\) = speed of the particle at the point A)

or, \(v_A^2=\nu^2+2 g \cdot A C\)

Here, \(A C=O A-O C=O A-O B \cos \theta\)

= \(l-l \cos \theta=100-100 \cos 60^{\circ}=50 \mathrm{~cm}\)

∴ \(v_A^2=(200)^2+2 \times 980 \times 50=13.8 \times 10^4\)

or, \(v_A=371.5 \mathrm{~cm} \cdot \mathrm{s}^{-1} \text {. }\)

Tension In Vertical Circular Motion Class 11

Example 3. A body slides down an inclined plane after being released from rest from a height h and finally, it describes a circle of radius r instead of travelling along a horizontal floor. For what minimum value of h, can the particle describe that motion? Ignore friction.
Solution:

Given

A body slides down an inclined plane after being released from rest from a height h and finally, it describes a circle of radius r instead of travelling along a horizontal floor.

After descending along the inclined plane, the body can describe the circular path if the velocity of the body at the lowest point B of the circular path is, at least, v = \(\sqrt{5 g r}\).

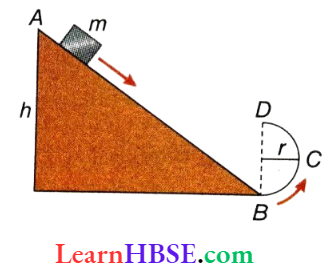
The kinetic energy of the body at the point B

= \(\frac{1}{2} m v^2=\frac{1}{2} m \cdot 5 g r=\frac{5}{2} m g r\)

The falling body will acquire this kinetic energy in exchange for the potential energy that it possesses at the height h.

So, \(\frac{5}{2} m g r\) = mgh or, h = \(\frac{5}{2}\)r

Derivation Of Vertical Circular Motion Class 11

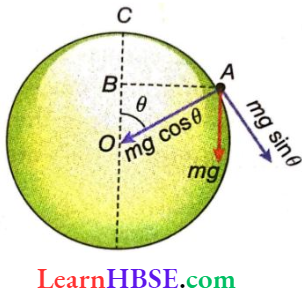
Example 4. A body starts falling from the top of a smooth sphere of radius r. What angle does the body subtend at the center of the sphere when it just loses contact with the sphere and what will be its velocity then?
Solution:

Given

A body starts falling from the top of a smooth sphere of radius r.

Let the angle subtended by the body at the center of the sphere when it loses contact with the sphere be θ. The body just loses contact with the sphere when the component of gravitational force cannot provide the necessary centripetal force to the body so that it can continue in the circular path.

Numerical Problems On Vertical Circular Motion Class 11

So, according to mgcosθ = \(\frac{mv^2}{r}\)……(1)

(v = velocity of the body when it just loses contact with the sphere)

According to the principle of conservation of energy, \(\frac{1}{2}\)\({mv^2}\)= mgr(1-cosθ)

[OC = OA – r, OB = rcosθ, BC = OC- OB – r- rcosθ = r(1 – cosθ)]

or, v² = 2gr(1 – cosθ)…(2)

From equations (1) and (2) we get, mg\(\cos \theta=\frac{m}{r} \cdot 2 g r(1-\cos \theta)\)

or, \(\cos \theta=2(1-\cos \theta)\)

or, \(\cos \theta=\frac{2}{3} \quad \text { or, } \theta=\cos ^{-1} \frac{2}{3}=48.2^{\circ}\)

Again, \(v^2=2 g r(1-\cos \theta)=2 g r\left(1-\frac{2}{3}\right)=\frac{2}{3} g r \)

∴ v = \(\sqrt{\frac{2}{3} g r .}\)