Haryana Board Solutions For Class 7 Maths Chapter 3  Data Handling

Key Concepts

• Data:
  A data is a collection of numbers gathered to give some information.
• We collect data by several ways. They are through newspapers, magazines, television and through various sources. All the data collected give us some sort ofinformation.
• Collection of Data:
  Any set of data can give us some inferences butifwe want tofind a specific information,we need to collect data which can tell us about that. Some of these data are easy to collect and some are difficult.
  Below are given a few situations:
  Performance of your class in Mathematics.
  Performance of India in football or in cricket.
  Female literacy rate in a given area.
  Number of children below the age of 5 years in the families around the area.
• Organization of Data:
  After collecting the data we have to record and organize it.
  Different kinds of data we come across in our daily life are put in a tabular form. Our school rolls, progress report, indexin the text books, temperature record and many other are recorded in a tabular form.
  If we record them in a proper table it becomes easy to understand and interpret.
• The information eitherin theform ofpictures,numbers or words is called ‘Data’.
• Based on method of collecting information the data is divided into two different types namely, ‘Primary data’ and ‘Secondary data’.
• Primary Data: The data collected directly through personal experiences, interviews, direct observations etc., is called ‘Primary data’.It is also called ‘raw data’ or firsthand’ information.
• Secondary Data: The information which has been collected in the past by someone else but used by the investigator is called ‘Secondary Data’.
• Range of the data: The difference between maximum and minimum values of data is called ‘Range’ of the data.
• Measures of Central Tendency:  Arithmetic mean, mode, and median.
• Arithmetic mean (or) Average:  The sum of observations ofdata is divided by number of observations of a data is called Arithmetic mean (or) Average (or) Mean.
  \( \text { Arithmetic mean }=\frac{\text { Sum of observations }}{\text { Number of observations }} \)
• ‘Arithmetic Mean’ is a number or value that represents or shows the central tendency of a group of observations of data.
• ‘Arithmetic Mean’ of given data always lies between the highest and lowest observations of the data.
• The most common representative (or) central tendency value of a grouped data is average or Arithmetic mean.
• Mode: The observation which occurs most frequently in the given data is called ‘Mode’ of the data.
• Data having only one mode, is known as ‘Unimodal data’.
• Data having two modes is known as ‘Bimodal data’.
• Median: The middle most value of the data, when the observations are arranged in either ascending or descending order is called ‘median’.
• If the number of observations is odd then median is \( \left(\frac{(n+1)}{2}\right)^{\text {th }} observation. \)
• If the number of observations is even then the median is average of \( \left(\frac{\mathrm{n}}{2}\right)^{\mathrm{th}} \) and \( \left(\frac{n}{2}+1\right)^{t h} \) observation.
• Bargraph: Representation o fnumerical data by using bars of uniform width is called ‘Bar graph’.
• In bar graphs the width of all rectangles (bars) is equal and height (lengths) of each bar is proportional to the data that it represents.
• Double bar graph: Representation of two sets ofnumerical data on the same graph by using bits of uniform width is called double
  bar graph.
• Pie charts: A pie chart is the representation ofthe numerical data by sectors ofthe circle such that angle ofeach sector(area ofsector) is proportional to value of the given data.
• The parts ofcircles are called ‘sectors’
• Angle of sector
  \( =\frac{\text { Value of the item }}{\text { Sum of the values of all items }} \times 360^{\circ} \)
• It You will find that when all the values of data set are increased or decreased by a certain number, the mean also increases or decreases by the same number.
• Note: If each observation in a data set is repeated an equal number of times or if no score is repeated then the data set has no mode.

1. How would you find the average of your study hours for the whole week?

Solution: First,I will find the study hours of all the 7 days of the week separately.

Then find the sum of all these study hours and divide by 7.

1. Find the mean of your sleeping hours during one week.

Solution: Students can arrange the data with the help of their parents and then solve with the help of teacher.

2. Find at least 5 numbers between \( \frac{1}{2} \) and \( \frac{1}{3} \)

Solution: 1st number

2nd number

3rd number

4th number

5th number

The required five numbers are:

Haryana Board Solutions For Class 7 Maths Chapter 3  Data Handling Exercise-3.1

1. Find the range of heights of any ten students of your class.

Solution:

Let’s assume we have the following heights (in cm) for ten students

145, 150, 142, 155, 148, 160,135, 155, 140,165

Range = 165 cm- 135 cm

= 30 cm

HBSE Class 7 Data Handling Solutions

2. Organise the following marks in a class assessment, in a tabular form.

4, 6, 7, 5, 3, 5, 4, 5, 2, 6, 2, 5,1, 9, 6, 5, 8, 4, 6, 7

The frequency table:

1) Which number is the highest?

Solution: 9

2) Which number is the lowest?

Solution: 1

3) What is the range of the data?

Solution: Range = Highest observation.

Lowest observation = 9-1=8

Haryana Board Class 7 Maths Data Handling Solutions

4) Find the arithmetic mean.

Solution: Arithmetic mean

3. Find the mean of the first five whole numbers.
Solution: First five whole numbers are 0, 1, 2, 3, 4

4. A cricketer scores the following runs in eight innings: 58,76,40,35, 46,45,0,100. Find the mean score.

Solution: Given observations: 58, 76, 40, 35, 46, 45, 0, 100

5. Following table shows the points of each player scoredin four games.

Solution:

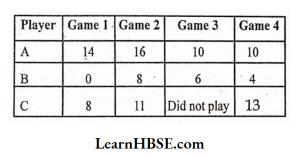
Now answer the following questions:

1) Find the mean to determine A’s average number of points scored per game.

Solution: Points of A in all the four games’are 14, 16, 10, 10

2) To find the mean number of points per game for C, would you divide the total points by 3 or by 4 ? Why ?

Solution: To find the mean number of points per game for C we divide the total points by 3 because the number of games under consideration is 4 but ‘C’ did not play the 3rd game.

Key Questions in Data Handling for Class 7 HBSE

3) B played in all the four games. How would you find the mean ?

Solution: Points of B in all the four games are 0, 8, 6, 4

4) Who is the best performer?

Solution:

A’s average =12.5

B’s average =4.5

C’s average = \( \frac{8+11+13}{3}=\frac{32}{3}=10.67 \)

A is the best performer.

Class 7 Maths Chapter 3 Data Handling Haryana Board

6. The marks (out of 100) obtained by a group of students in a science test are 85, 76, 90, 85, 39, 48, 56, 95, 81 and 75.

Find the:

1) Highest and the lowest marks obtained by the students.

Solution:

Highest marks obtained by the students = 95

Lowest marks obtained by the students = 39

2) Range of the marks obtained.

Solution:

Range = Highest marks- Lowest marks = 95 – 39 = 56

3) Mean marks obtained by the group

Solution:

7. The enrolment in a school during six consecutive years was as follows: 1555, 1670, 1750, 2013, 2540, 2820. Find the mean enrollment of the school for this period.

Solution:

8. The rainfall (in mm) in a city on 7 days of a certain week was recorded as follows:

1) Find the range of the rainfall in the above data.

Solution:

Range of the rainfall

Highest rainfall – Lowest rainfall

= 20.5 – 0.0- 20.5 mm

2) Find the mean rainfall for the week.

Solution: Mean rainfall for the week

Sample Problems Data Handling Haryana Board Class 7

3) On how many days was the rainfall less than the mean rainfall?

Solution:

On 5 days the rainfall is less than the mean rainfall.

The heights of 10 girls were measured in cm and the results are as follows: 135, 150, 139’ 128, 151, 132, 146, 149, 143,141.

1) What is the height of the tallest girl?

Solution: Height of the tallest girl – 151 cm

2) What is the height of the shortest girl?

Solution. Height of the shortest girl = 128

3) What is the range of the data?

Solution: Range of the data = Highest observation – Lowest observation=151-128 = 23 cm

Haryana Board 7th Class Maths Data Handling Questions and Answers

4) What is the mean height of the girls?

Solution: Mean height of the girls

5. How many girls have height more than the mean height ?

Solution: 5 girls have heights more than the mean height

Solutions To Try These

Find the mode of

1) 2, 6, 5, 3, 0,3, 4, 3, 2, 4, 5, 2, 4.

Solution: Arranging the numbers with same values together, we get 0,2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 6.

Mode of this data are 2, 3, 4 because they occur most often.

2) 2, 14, 16, 12, 14, 14, 16, 14, 10, 14, 18, 14.

Solution: Arranging the numbers with same values together we get 2, 10, 12, 14, 14, 14, 14, 14, 14, 16, 16, 18

Mode of this data is 14

Solutions To Try These

1. Find the mode of the following data: 12, 14, 12,16, 15, 13,14, 18, 19, 12, 14, 15, 16, 15, 16,16, 15,17, 13, 16, 16, 15, 15, 13, 15,17,15, 14, 15,13, 15, 14.

Solution: Let us put the data in a tabular form:

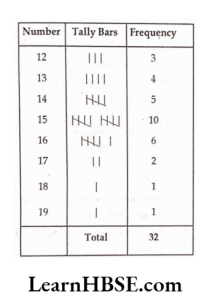
Mode of this data is 15.

2. Heights (in cm) of 25 children are given below: 168, 165, 163, 160, 163, 161, 162, 164, 163, 162, 164, 163, 160, 163, 160, 165, 163, 162, 163, 164, 163, 160, 165, 163, 162. What is the mode of their heights? What do we understand by mode here?

Solution: Arranging the data in ascending order :

160, 160, 160, 160, 161, 162, 162, 162, 162, 163, 163, 163, 163,163, 163, 163, 163, 163, 164, 164, 164, 165, 165, 165, 168.

Here 163 cm occurred the highest number of times.

Mode = 163

We understand that most of the students have height of 163 cm.

Solutions To Try These

Discuss with your friends and give

1) Two situations where mean would be an appropriate representative value to use, and

2) Two situations where mode would be an appropriate representative value to use.

Solution:

1) Two situations where mean would be appropriate:

1. Average grades

2. Age distribution

2) Two situations where mode would be appropriate:

1. Preferred mode of transportation

2. Clothing sizes

In these situations, the mean is suitable for calculating the average or overall value, while the m useful for identifying tire most frequently occurring value in the dataset.

Solutions To Try These

Your friend found the median and the mode of a given data. Describe and correct your friends error if any : 35, 32, 35, 42, 38, 32, 34 Median 42, Mode  32

Solution: Arranging the data in ascending order :

32, 32, 34, 35, 35, 38, 42

Median is the middle observation

Median =35

Here 32, 35 occurred two times

Mode – 32, 35

Haryana Board Class 7 Data Collection and Organization

Haryana Board Solutions For Class 7 Maths Chapter 3  Data Handling Exercise-3.2

1, The scores in Mathematics test (out of 25) of 15 students is as follows: 19, 25, 23, 20, 9, 20, 15, 10, 5, 16, 25, 20, 24, 12, 20. Find the mode and median of this data Are they same?

Solution: Given scores: 19, 25, 23, 20, 9, 20,15, 10, 5, 16, 25, 20, 24, 12, 20

Median: Arranging the data in ascending order: 5, 9, 10, 12, 15, 16,19, 20, 20, 20, 20, 23, 24, 25, 25

Median is the middle observation.

Median = 20

Mode: 20 occurred more frequently

A Mode =20

Yes, median and mode of the given scores are same.

2. The rims scored in a cricket match by 11 players is as follows: 6, 15, 120, 50, 100, 80, 10, 15, 8, 10, 15 Find the mean, mode and median of this data. Are the three same ?

Solution:

Given: Runs scored in a cricket match by 11 players 6, 15, 120, 50, 100, 80, 10, 15,8,10,15.

1) Mean:

∴ Mean = 39

2) Median:

Arranging the datain ascending order : 6, 8, 10, 10, 15, 15, 15, 50, 80, 100, 120

Median is the middle observation.

Median = 15

3) Mode:

Mode is the observation with highest frequency.

Mode = 15

Here mean, mode and median are not same

Chapter 3 Data Handling Class 7 Solutions in Hindi Haryana Board

3. The weights (in kg.) of15 students of a class are: 38, 42/ 35, 37, 45, 50, 32, 43, 43, 40, 36, 38, 43, 38, 47

1) Find the mode and median of this data.

2) Is there more than one mode?

Solution:

1) The weights (in kg.) of 15 students of a class. 38, 42, 35, 37, 45, 50, 32, 43, 43, 40, 36, 38, 43, 38, 47

Median:

Arranging the grades in ascending order: 32, 35, 36, 37, 38, 38, 38, 40, 42, 43, 43, 43, 45, 47, 50

∴ Median = 40

Mode: It is the observation with highest frequency

Mode = 38 ;43

2) Yes there are two modes. i.e. 38 and 43.

4. Find the mode andmedian of the data: 13, 16,12,14, 19, 12, 14, 13, 14

Solution:

Given data:13,16,12,14,19,12,14,13,14 Median:

Arranging the data in ascending order: 12,12,13,13,14,14,14,16,19

Median = 14

Mode: It is the observation with highest frequency.

Mode = 14

5. Tell whether the statement is true or false:

1) The mode is always one of the                                                                         – True

2) The mean is one of the numbers in a data.                                                      – False

3) The median is always one of the numbers in a data.                                           -True

4) The data 6, 4, 3, 8, 9, 12, 13, 9 has mean 9.                                                  – False

Solutions To Try These

1. The bar graph shows the result of a survey to test water-resistant watches made by different companies. Each of these companies claimed that their watches were water-resistant. After a test the above results were revealed.

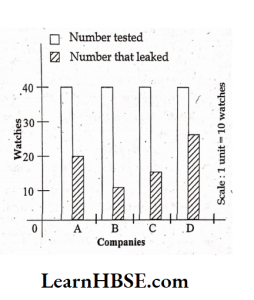
1) Can you work out a fraction of the number of watches that leaked to the number tested for each company?

Solution: In scale:1 unit = 10 watches

For company A: Required ratio

For company B: Required ratio

For company C: Required ratio

For company D: Required ratio

2) Could you tell on this basis which company has better watches?

Solution: Company B has better watches.

2. Sale of English and Hindi books in the years 1995,1996,1997 and 1998 are given below:

Draw a double bar graph and answer the following questions

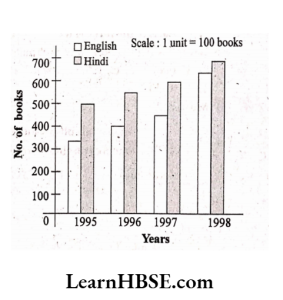
1) In which year was the difference in the sale of the two language books least?

Solution:

Difference

In 1995 —> 500-350 = 150

In1996 —> 525 – 400 = 125

In 1997 —> 600- 450 = 150

In 1998 —> 650-620 = 30

In the year 1998 the difference in the sale of two language books is least

2) Can you say that the demand for the English books rose faster? Justify.

Solution: Yes, we can say that the demand for English books rose faster.

Haryana Board Solutions For Class 7 Maths Chapter 3  Data Handling Exercise-3.3:

1. Use the bar graph to answer the following questions.

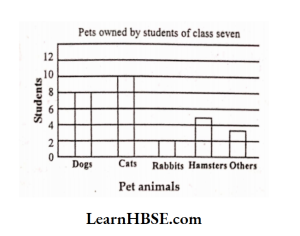
1) Which is the most popular pet?

Solution: ‘Cat’ is the most popular pet.

2) How many students have dog as a pet?

Solution: 8 students have a dog as a pet.

2. Read the bar graph which shows the number of books sold by a bookstore during five consecutive years and answer the following questions:

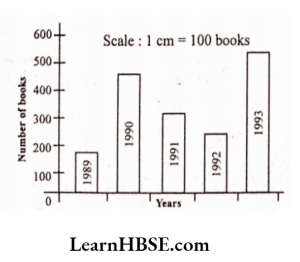
Haryana Board Class 7 Maths Exercise 3.1 Solutions

1) About how many books were sold in 1989? 1990? 1992?

Solution: Number of books sold in 1989 = 175 (approx)

Number of books sold in 1990 = 475 (approx)

Number of books sold in 1992 = 225 (approx)

2) In which year were about 475 books sold? About 225 books sold?

Solution:

About 475 books were sold in 1990.

About 225 books were sold in 1992.

3) In which years were fewer than 250 books sold ?

Solution: In the years 1989 and 1992 fewer than 250 books were sold.

4) Can you explain how you would estimate the number of books sold in 1989?

Solution: From the bar graph reading it is clear that the number of books in 1989 is 175.

3. Number of children in six different classes are given below. Represent the data on a bar graph.

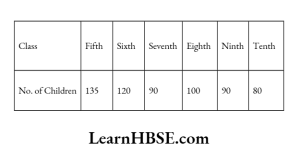
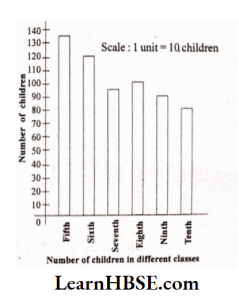
1) How would you choose a scale?

Solution: Start the scale at ‘O’.

The greatest value in the given data is 135. So mark the scale at the value greater than 135 such as 140. Use equal division along axes such as an increment of 10. Take 1 unit for 10 children.

2) Answer the following questions:

1) Which class has the maximum number of children ? And the minimum ?

Solution:

Fifth class has the maximum number of children.

Tenth class has the minimum number of children.

2) Find the ratio of students of class sixth to the students of class eight.

Solution: Ratio of students of class sixth to eighth = 120 : 100

4. The performance of a studentin l9t term and 2nd term is given. Draw a double bar graph choosing appropriate scale and answer the following:

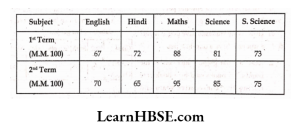
Solution:

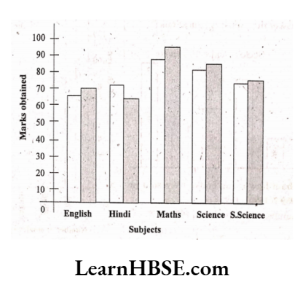
1) In which subject, has the child improved his performance the most ?

Solution: In Maths the child has improved his performance the most.

2) In which subject is the improvement the least ?

Solution: HisScience the child’s improvement is the least.

3) Has the performance gone downin any subject ?

Solution: Yes, his performance has gone downin Hindi.

5. Consider this data collected from a survey of a colony.

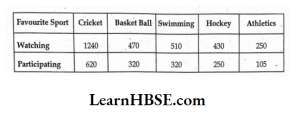
1) Draw a double bar graph choosing an appropriate scale. What do you infer from the bar graph?

Solution:

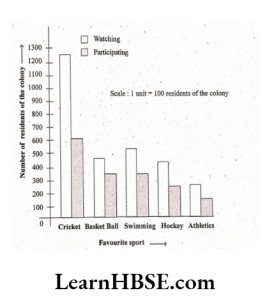
Inference: The residents of the colony like cricket the most and athletics tire least

2) Which sport is most popular?

Solution: Cricket is most popular watching as well as participating.

3) Which is more preferred, watching or participating in sports?

Solution: Watching sports is more preferred than participating in sports.

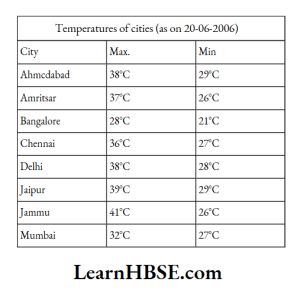
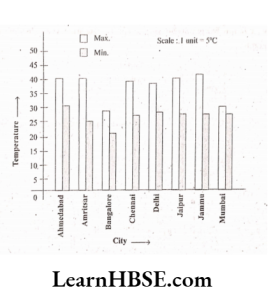
6. Take the data giving the minimum and the maximum temperature of various cities given in the beginning of this chapter. Plot a double bar graph using the data and answer the following:

HBSE Class 7 Maths Chapter 3 Guide

1) Which city has the largest difference in the minimum and maximum temperature on the given data?

Solution:

Ahmedabad → 38°- 29° = 9°C;

Bangalore → 28°- 21° = 7°C;

Delhi → 38°-28° =10°C ;

Jammu → 41°- 26° = 15°C;

Amritsar → 37°- 26°= 11°C

Chennai → 36°- 27° = 9°C

Jaipur → 39°- 29° = 10°C

Mumbai → 32°- 27° = 5°C

Jammu has the largest difference in the minimum and maximum temperatures on the given data.

2) Which is the hottest city and which is the coldest city?

Solution: Jammu is the hottest city and Bangalore is the coldest city.

3) Name two cities where maximum temperature of one was less than the minimum temperature of the other.

Solution: Bangalore and Ahmedabad orBangalore and Jaipur.

4) Name the city which has the least difference between its minimum and the maximum temperature.

Solution: Mumbai.

Additional Questions

Haryana Board Solutions For Class 7 Maths Chapter 3  Data Handling Very Short Answer Questions

1. What is meant by a data?

Solution:

A data is a collection of numbers gathered to give some information.

2. Define ‘Range’ of a data.

Solution:

The difference between the highest and the lowest observations of a data is called range

3. Find the arithmetic mean of 17, 31, 12,27,15,19,23

Solution:

4. Find the range of the scores 18, 26, 23,16, 32, 18

Solution:

Range = Highest observation- Lowest observation

32-16 = 16.

Important Questions for Class 7 Maths Chapter 3 Haryana Board

5. Find the mode of the numbers 10, 8, 4,6, 10, 3, 10.

Solution:

Here 10 occurs 3 times

Mode = 10

6. Define ‘Median’.

Solution:

The data is arranged in the order of increasing or decreasing magnitude then the middle most value in this arrange ment is called median.

7. Find the median of 10, 20, 15, 29, 35,42, 14.

Solution: The values are arranged in increasing order 10,14,15, 20, 29,35, 42 Then the middle most value 20 is the median.

8. Find the arithmetic mean of first three multiples of 5.

Solution:

First three multiples of 5 are = 5, 10, 15

Arithmetic mean

9. What is the range of first ten whole numbers ?

Solution: First ten whole numbers are 0,l, 2, 3, 4,5, 6, 7, 8 and 9

Range

= Maximum value – minimum value

=9-0=9

10. Find the mean of the first five prime numbers.

Solution:

The numbers are 2, 3, 5, 7, 11

Sum ofnumbers = 2 +.3 + 5 + 7+11 = 28

11. Amounts donated by eight students to ‘NIVAR’ cyclone effected people are 300, 450, 700, 650, 400, 900, 850. Find the Arithmetic Mean of amounts donated.

Solution: The amounts donatedby eight students are 300, 450,700, 650, 400, 750, 900,850.

Number of students = 8

Arithmetic mean of amounts donated

\( =\frac{5000}{8} \) = 625.

12. 20 students were participated in “SWATCH BHARAT ABHIYAN” campaign. The number of days each student participated were 5,1, 2, 4,1, 2, 3, 2,1, 2, 3, 2, 5, 3, 4, 2,1, 3, 4 and 5. Find mode of the data.

Solution: The number of days each student participated were 5,1, 2, 4,1, 2, 3, 2,1, 2,3, 2, 5, 3, 4, 2, 1,3, 4 and 5.

By arranging the numbers of saipe values together.

1,1, 1,1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4; 4, 5,5,5.

‘2’ occcurs most frequentlyin the data.

Mode = 2.

13. The number of pages in textbooks of different subjects are 421,175, 128>117, 150, 145, 147 and 113 find median of given data.

Solution: The number of pages in textbooks of different subjects are 421, 175, 128, 117,150, 145, 147 and 113.

Arrange the observations in ascending order113,117,128,145,147,150,175, 421.

In ‘8’ observations the 4th and 5th observations are middle most values

14. In a set of four integers, the average of the two smallestintegers is 102, the average of the three smallest integers is 103, the average ofallfouris104. Which is the greatest of these integers ?

Solution:

Average of all four = 104

Total of four integers = 4 x 104 = 416

Total of three integers = 3 x 103 = 309

4th No = 416 -309 = 107

Total of two integers = 2 x 102 = 204

3rd No = 309- 204 = 105

Similarly 2nd is 103 & 1st is 101

The numbers are 101, 103, 105 & 107

Greatest = 107

15,. The monthly income (in rupees) of 7 households in a village are 1200, 1500, 1400,1000,1000,1600,10000. (1) Find the median income of the house holds, (2) If one more household with monthly income 1500is added, what will the median income be?

Solution: Monthly income (in rupees) are 1200, 1500, 1400, 1000, 1000, 1600, 10000

Rearrangingin ascending order, the income 1000, 1000, 1200, 1400, 1500, 1600 and 10,000

It can be seen 1400 is the median. By inclusion of one more item of 1500 and rearranging the incomes are 1000, 1000, 1200, 1400, 1500, 1500, 1600 & 10,000

From which we find both 1400 & 1500 are in the middle of the values.

The median, therefore is calculated by the average of the two middle values. i.e

The median income = 1450

16. How many distinct sets of three positive integers have a mean of 6, a median of 7, and no mode ?

Solution: Let the integers be x, y & z

such that mean, 6 = \( \frac{x+y+z}{3} \)

ie x + y + z = 18
given median = 7
x + z = 11
x & z may be
1, 10
2,9
3,8
4,7
&5,6

such that sets of three positive integers satisfying the data are

1, 7, 10 fulfilling the condition

2, 7, 9 of mean = 6

3, 7, 8 median = 7

Haryana Board Solutions For Class 7 Maths Chapter 3  Data Handling Long Answer Questions

17. Find arithmetic mean of

1) 4,5,11,8

2) 10, 15, 21, 12, 17

3) \( \frac{1}{4}, \frac{1}{2}, \frac{3}{4}, \frac{3}{2}, \frac{5}{4} \)

1) 4,5,11,8

Solution: Arithmetic mean

2) 10, 15, 21, 12, 17

Solution: Arithmetic mean

3.\( \frac{1}{4}, \frac{1}{2}, \frac{3}{4}, \frac{3}{2}, \frac{5}{4} \)

Solution: Arithmetic mean

18. In the adjacent double bar graph, number of students of a class are shown according to academic year.

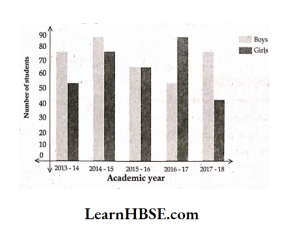
Answer the following questions on the basis of this double bar graph.

1) In which academic year, number of girls were more than number of boys in the school ?

Solution. In 2016-17 academic year,number of girls weremore thannumber of boys in the school.

2) In which academic year, number of both girls and boys in the school were equal?

Solution: In 2015-16 academic year, number of both girlsand boysin the school were equal.

3) What was the total number of students in the school in the academic year 2013-14?

Solution. Total number of students in the academic year 2013-14 was =70 + 50 = 120.

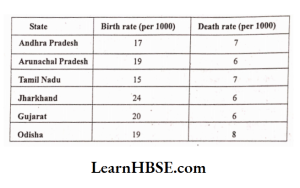
19. Birth and death rates of different states in 2015 are given below. Draw a double bar graph for the given data.

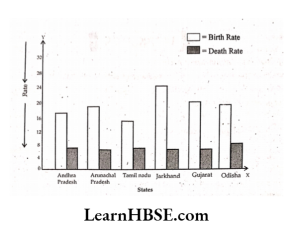
Solution:

Steps in drawing a double bar graph:

1. Draw X-axis (horizontal line) and Y-axis (vertical line) on the graph paper and mark their intersecting point as ‘O’.

2. Take ‘States’ on X-axis

3. Take ‘Birth rate’ and ‘Death rate’ on Y-axis.

4. Take an appropriate scale on Y-axis so that birth rate and death rate can be shown easily. Let us take 1 cm = 2 units on Y-axis.

5. Find the lengths of each bar by dividing the value by 2

Example: Length of bar represents 17 birth

rate = \( \frac{17}{2} \) = 8.5 cm

Length of bar represents 7 death rate = \( \frac{7}{2} \) = 8.5 cm

=3.5 cm.

Important Concepts Data Handling Class 7 HBSE

20. Draw a bar graph for the following data.

Population of India in successive census years.

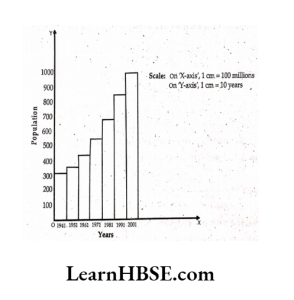
Source: Data from census of India 1991 and 2001

Solution:

Draw X- axis (horizontalline) and Y- axis (verticalline) on the graph paper and mark their intersection as O.

Take years on X – axis

Take population on Y – axis with1 cm as 100 millions so that maximum population fits on the graph sheet.

Graph is drawn against the given values.

Haryana Board Solutions For Class 7 Maths Chapter 3  Data Handling Multiple Choice Question And Answers

1. Which of the following is not a measure of central tendency?

1. Mean
2. Median.
3. Mode
4. Range

Answer: 4

2. Range of 3, 50, 6, 19, 5, 43, 2 is 

1. 52
2. 48
3. 53
4. 46

Answer: 2

3. Mean of first 5 prime numbers is

1. 6.5
2. 5.2
3. 5.6
4. 6.2

Answer: 3

4. Mode of the data 14, 6, 12, 6, 13, 6, 14, 6

1. 6
2. 12
3. 13
4. 14

Answer: 1

5. Median of x, \(\frac{x}{2}, \frac{x}{3}, \frac{x}{4}, \frac{x}{5} \) is 5. Then x =

1. 3
2. 9
3. 12
4. 15

Answer: 4

6. Mean of three observations a, b, c is…………

1. \( \frac{a+b+c}{3} \)
2. \( \frac{\mathrm{a} \times \mathrm{b} \times \mathrm{c}}{3} \)
3. \(\frac{a-b-c}{3} \)
4. \(\frac{a \times b+c}{3} \)

Answer: 1

7. The bar graph shows mode of transport to a school. Here, the total no. of students is……………

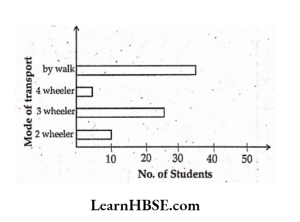
1. 50
2. 80
3. 75
4. 100

Answer: 3

Step-by-Step Solutions for Data Handling Class 7 Haryana Board

8. Given below are heights of10 boys of class 7in cm138,128,140,142,129,142,154,144,146, 152. Then the median height is ………….cm

1. 142
2. 140
3. 144
4. 146

Answer: 1

9. The bar graph consists of………..

1. triangles
2. squares
3. circles
4. rectangles

Answer: 4

10. The bar graph shows, the number of hours studied by Arjun everyday during last 4 years. The mode of the given data belongs to………. year

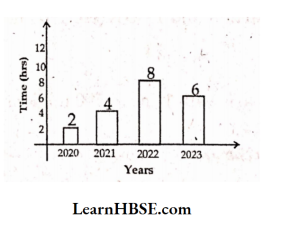
1. 2021
2. 2022
3. 2023
4. 2020

Answer: 2

11. The mean of first 5 multiples of 6 is

1. 12
2. 18
3. 24
4. 30

Answer: 2

12. Match the following for the given data: -2, 0, 1, 2, 9, 2, 5, 2, -6, -1

a) Mean       ( )    1)2

b) Median   ( )    2)15

c) Mode      ( )     3)1.2

d) Range    ( )    4)1.5

1. a-1,b-2, c-3, d-4
2. a – 2,b – 3, c – 4, d -1
3. a-4,b-1, c-2, d-3
4. a-3,b-4,c-1, d-2

Answer: 4

13. Which of the following has the same mean, median and mode ?

1. 2, 3, 7, 3, 8, 2, 3
2. 4, 3, 4, 3, 4, 6, 4
3. 4, 2, 2,1,3, 2, 3
4. 6, 2, 5, 4, 3, 4,1

Answer: 2

14. If the arithmetic mean of 5, 6, 2, x, 12 is 8, then x =………..

1. 10
2. 12
3. 8
4. 15

Answer: 4

15. The range of the data 6, 3, 0, -5,12, -4 if 2 was subtracted from each of the observations becomes….

1. increases
2. decreases
3. does not change
4. zero

Answer: 3

16. Given graph shows the marks of a student in Sumniative Assessment. The average marks of the student is…………

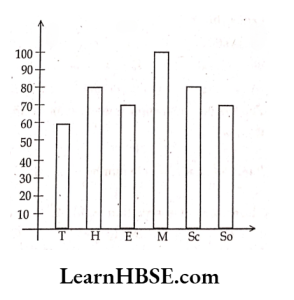
1. 76.6
2. 75.6
3. 77.6
4. 76

Answer: 1

17. The median of the data 5, 9, 0, -6, x, 6,1 if their mean is 2 is…………

1. 0
2. 1
3. 2
4. 3

Answer: 2

18. The mean offirst two numbers is 2.5, the mean of other three numbers is 9, then mean of all numbers is

1. 6.4
2. 6.5
3. 5.9
4. 5.2

Answer: 1

19. For the given data: 3, 5, 6, 3, 4, 3, 2, 6, the mean of its median and mode is

1. 3.2
2. 3.5
3. 3.25
4. 4

Answer: 3

20. In bar graphs………of bars remains some

1. length
2. width
3. value
4. none

Answer: 2

21. Study the bar graph. The average circulation of newspapers B and C in the month of June is………..

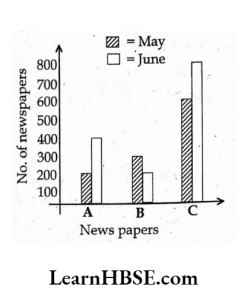
1. 450
2. 500
3. 550
4. 475

Answer: 2

22. A vegetable seller collects the following data of vegetables sold in his shopin a day. The mode (most sold vegetable) of the data is ……..

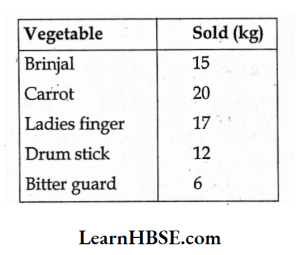
1. Drumstick
2. Brinjal
3. Ladies Finger
4. Carrot

Answer: 4

23. The weights of 6 people is given as 38, 42,18, 35, 35, 39, then the mean weight of them is

1. 35.4
2. 39
3. 35
4. 34.5

Answer: 4

24. Range of first 10 whole numbers

1. 0
2. 11
3. 9
4. 10

Answer: 3

25. The median of observations 8, 10, 12, x + 1, x+3, 25, 29, 35 is 18, then x =

1. 15
2. 16
3. 17
4. 18

Answer: 2

26. What is the arithmetic mean of first 10 natural numbers?

1. 3.5
2. 7.5
3. 55
4. 5.5

Answer: 4

27. The mean of 2, x, 5, y and 14 is 6 then which of the following is true?

1. x + y = 13
2. x + y = 9
3. x- y = 12
4. 2x + y = 13

Answer: 2

28. Find the arithmetic mean of first 6 prime numbers.

1. 5.83
2. 8.63
3. 6.83
4. 9.63

Answer: 3

29. Find the mean of first five whole numbers.

1. 1
2. 2
3. 3
4. 4

Answer: 2

30. Find the mean of first 6 natural numbers.

1. 5.5
2. 6.5
3. 3.5
4. 4.5

Answer: 3

31. The median of first 16 whole numbers is

1. 6.5
2. 7.5
3. 9.5
4. 8.5

Answer: 2

32. What is the shape of each partin pie chart ?

1. Sector
2. Chart
3. Cone
4. Cylinder

Answer: 1

33. The median of the data 24, 29, 34, 38, x is 29, then value of x is

1. more than 38
2. less than 29
3. between 29,34
4. none of these

Answer: 2

34. Total data is represented as relative size of components in a

1. Pie diagram
2. Pictograph,
3. Bar graph
4. Sector

Answer: 1

35. The most frequently occurring value for a set of observations is called

1. Arithmetic mean
2. Median
3. Mode
4. Range

Answer: 3

36. The median of first 5 even natural numbers

1. 6
2. 8
3. 10
4. 30

Answer: 1

Practice MCQ’s Handling Class 7 Haryana Board

37. The sum of four observations is 44. What is the mean ?

1. 10
2. 9
3. 8
4. 11

Answer: 4

38. The mean of 11 observations is 12. What is the sum of observations?

1. 122
2. 132
3. 142
4. 152

Answer: 2

In a survey finding, number of people watching TV serials aregiven below. Answer the following questions (39 – 40)

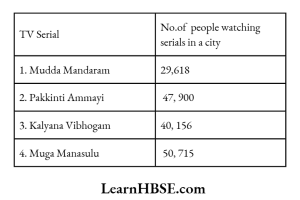
39. Which is the “most popular show” from the above table?

1. Mudda Mandaram
2. Pakkinti Ammay
3. Kalyana Vibhogam
4. Muga Manasulu

Answer: 4

40. Which concept is used to know “most popular show” ?

1. Mean
2. Median
3. Mode
4. None

Answer: 3

State which representative has to be taken to decide in the folloivittg situations (41-43).

41. Aninvigilator wants to bring sufficient number of additional papers to the examination hall.

1. mean
2. mode
3. median
4. none

Answer: 1

42. Preparation of number of laddus for a marriage

1. mean
2. mode
3. median
4. none

Answer: 1

43. For finding the favourite cricketer in a class

1. mean
2. mode
3. median
4. None

Answer: 2

44. Find the median of first five odd natural numbers.

1. 5
2. 4
3. 2
4. 8

Answer: 1

45. What is the mode ofunit digits that are presentin the numbers between 50 to 60 ?

1. 1
2. 5
3. 2
4. Nil

Answer: 4

46. When there is no mode for a particular data we can say the mode is

1. 1
2. 0
3. 2
4. None

Answer: 4

47. What is the mean of factors of 12 ?

1. 5.66
2. 3.76
3. 4.66
4. 8.66

Answer: 3

48. What is median of first 5 multiples of 11?

1. 32
2. 33
3. 34
4. 35

Answer: 2

49. The mean of x+2, x+7, x+6 is 15. Then find the observations.

1. 11,12,16
2. 12, 17, 16
3. 13,16,17
4. 15, 16, 17

Answer: 2

Weight of food that Raj ate each day is given in the table

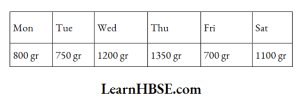
50. How much weight of food per day does he eat on an average?

1. 783.13
2. 873.3
3. 983.3
4. 784.3

Answer: 3

The following table shows the scores of player in each game. Observe it and answer the following questions. (51 – 52)

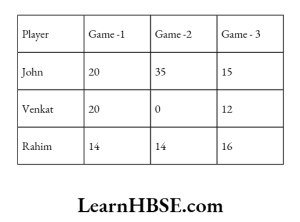
51. Who is the best player?

1. John
2. Venkat
3. Rahim
4. All

Answer: 1

52. Which mathematical concept is used to know the best player?

1. Mean
2. Median
3. Mode
4. All

Answer: 1

53. Identify the one which is not affected by maximum and minimum value of the data.

1. Mean
2. Mode
3. Median
4. None

Answer: 3

54. Find the difference between mean and median of the following data 3, 16, 24, 13

1. 1.5
2. 2.5
3. 0.5
4. 3.0

Answer: 3

Observe the table and answer 55, 56 questions based on this table.

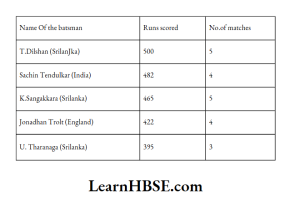
55. Who is the best batsman from the table?

1. T.Dilshan
2. Sachin Tendulkar
3. K.Sangakkara
4. Tharanga

Answer: 4

56. Who is average batsman?

1. Sachin Tendulkar
2. Jonadhan ,
3. K. Sangakkara
4. T. Dilshan

Answer: 2

57. Nani Practices Yoga regularly for a week as follows.

The average time spent per day by Nani is ….

1. 25 min
2. 32 min
3. 24 min
4. 30 min

Answer: 4

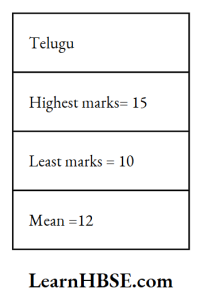
58. From this what can you conclude? ( )

1. Mean is nothing but average
2. Mean always lies between the highest and lowest observations of the data
3. Mean is representative of data
4. None

Answer: 2

59. A data of 10 observations has a minimum value 15 and maximum value 25. What is the mean of the data?

1. 12
2. 15
3. 21
4. 27

Answer: 3

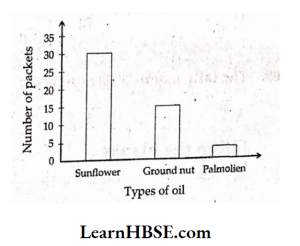
60. From the graph what is the mode here?

1. Sunflower
2. Groundnut
3. Palmolien
4. All

Answer: 1

61. The presentation of data can be of ………

1. Bar graph
2. Double bar graph
3. Pie chart
4. Above all

Answer: 4

Observe the graph and answer the following questions. (62- 63)

62. Find the ratio between sale of Jowar and sale of Sugar ?

1. 10: 5
2. 2:1
3. 2:3
4. A and B

Answer: 4

63. How much is the sale of Rice more over Wheat?

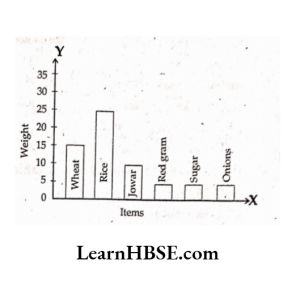
1. 5
2. 10
3. 15
4. 20

Answer: 2

Observe the adjacentfigure and answer thefollowing questions. (64- 65)

64. What are the total marks of Vani in both Mathematics and Science?

1. 85
2. 70
3. 110
4. 100

Answer: 1

65. In which subject Raju is well

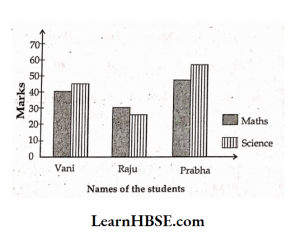
1. Maths
2. Science
3. Social
4. Telugu

Answer: 1

66. Mode of the given set of numbers 1,1, 1, 2, 2, 2, 2, 3, 3, 4, 4, is

1. 1
2. 2
3. 3
4. 4

Answer: 2

67. The most common representative value of a group of a data is

1. Arithmetic mean
2. Range
3. Mode
4. Median

Answer: 1

68. The average of \( \) and \( \frac{1}{2} \)

1. \( \frac{1}{8} \)
2. \( \frac{1}{2} \)
3. \( \frac{3}{8} \)
4. \( \frac{3}{4} \)

Answer: 3

69. The tally marks ||||.||| represents

1. 7
2. 8
3. 9
4. 6

Answer: 2

Fill in the blanks:

70. We use…… for recording and organisation of data

Answer: Tally marks

71. In a bar graph …… of all the bars is same

Answer: Width

72. ……. help to compare two collections of data at a glance

Answer: Double graph

73…….. represents data in the form of pictures.

Answer: Pictograph

74. Representing the data with the help of bars is known as…………..

Answer: bar graph

Match the following:

75.

1. Mean of 5 and 11 is ( ) A) 20

2. Range of 23, 26, 28, 32, 54, 41 is ( ) B) 12

3. Median of 19, 25, 23, 20, 9, is ( ) C) 8

4. Mode of 12, 14, 12, 16, 12 is ( ) D) 10

5. The tally marks |||| |||| represents ( ) E) 31

Answer: 1. C 2. E 3. A 4. B 5. D

Haryana Board Class 6 Maths Solutions For Chapter 1 Knowing Our Numbers

• Numbers help us to count concrete objects.
• Numbers help us to say which collection of objects is bigger and arrange things in order first, second, etc.
• Ascending order: Ascending order means arrangement from the smallest to the greatest.
• Descending order: Descending order means arrangement from the greatest to the smallest.
• 99 is the greatest 2 – digit number.
• The greatest 3 digit number is 999.
• The next number which comes next to 9999 is 10000, is called ten thousand.
• The smallest 7 – digit number is ten lakh.
• The smallest 8 – digit number is one crore.
• 1 crore = 100 lakhs = 10,000 thousands.
• 1 billion = 1000 million
• Number system is backbone to mathematics.
• 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 are called digits. We write all numbers using these 10 digits.
• Zero was invented by an ancient Indian mathematician.
• The term ‘Predecessor’ means the number before a given number. Eg. In the numbers 48, 49, 48 is predecessor.
• The term ‘Successor’ means the number after a given number. Eg. In the number 48, 49, 49 is the successor.
• The value of each digit in a given number depends upon its place value of the number, proceeding from right to left, everytime the place value increases by 10 times.
• To find total number of same digit numbers = Greatest number – Smallest number + 1
• Methods of numeration are commonly of two types, they are
• Indian system of numeration (Hindu – Arabic)
• International system of numeration.
• The method of representing a number in digits or figures is called notation.
• The method of expressing a number in words is called numeration.
• Place value of a digit in a number = Its face value x Position value
• Place value chart of number in Indian system of numerations is given below.

Indian System Place Value Chart Table

• Place value chart of numbers in International system of Numerations is given below.

International system place value chart table

• Comparison of Indian and International system of numeration.

• • Note: 1 lakh = 100 thousands
  • 10 lakhs = 1 million
  • 1 crore = 10 millions
  • 10 crores = 100 millions
  • 100 crores = 1 billion
• To measure water flow we use ‘Cusecs’ and T.M.C.
  • Cusecs = Cubic feet per second
    = Flow of 28.316 litre per second
  • T.M.C = Thousand million cubic feet
    = 283160000000 litres.
• To measure the weights of products we use grams, kilograms, quintal, tonnes …… etc.
  • 1 kg = 1000 grams
  • 1 quintal = 100 kgs
  • 1 tonne = 1000 kgs
• To measure the distances we use mm, cm, m, km ….. etc.
• In order to estimate or round off a number to the nearest
  • a) Tens:
    • If the digit at ones place is less than 5, replace the one’s digit by zero, other digits remain same.
    • If the digit at ones place is greater than or equal to 5, increase tens digit by ‘1’, replace units digit by ‘0’. Other digits remain same.
  • b) Hundreds:
    • Observe the digit at tens place. If it is less than 5, then hundreds place remains same. Put zeroes in tens and units places.
    • If the digit at tens place is greater than or equal to 5 then add ‘1’ to hundreds place. Put zeroes in tens and units places.
• Observe the following table and fill with the appropriate numbers in the table and write in words.

Haryana Board Class 6 Maths Knowing Our Numbers Solutions

Question 1. Can you instantly find the greatest and the smallest numbers in each row?

1. 382, 4972, 18, 59785, 750.

Solution. Greatest number is 59785.

Smallest number is 18.

2. 1473, 89423, 100, 5000, 310.

Solution. Greatest number is 89423.

Smallest number is 100.

3. 1834, 75284, 111, 2333, 450

Solution. Greatest number is 75284.

Smallest number 111.

4. 2853, 7691, 9999, 12002, 124

Solution. Greatest number is 12002.

Smallest number is 124.

Was that easy? Why was it easy?

Solution. Yes! it was easy. We just looked at the number of digits and found the answer. The greatest number has the most thousands and smallest is only in hundreds or in tens.

Question 2. Find the greatest and the smallest numbers.

1. 4536, 4892, 4370, 4452

Solution. Greatest number is 4892;

Smallest number is 4370.

2. 15623, 15073, 15189, 15800

Solution. Greatest number is 15800;

Smallest number is 15073.

3. 25286, 25245, 25270, 25210

Solution. Greatest number is 25286;

Smallest number is 25210.

4. 6895, 23787, 24569, 24659

Solution. Greatest number is 24659;

Smallest number is 6895.

Place Value And Face Value Explained Class 6 HBSE

Question 3. Use the given digits without repetition and make the greatest and smallest 4-digit numbers (Hint: 0754 is a 3-digit number.)

a. 2, 8, 7, 4

Solution. Greatest four digit number = 8742;

Smallest four digit number = 2478.

b. 9,7,4,1

Solution. Greatest four digit number = 9741;

Smallest four digit number = 1479.

c. 4, 7, 5,0

Solution. Greatest four digit number = 7540;

Smallest four digit number = 4057.

d. 1,7,6,2

Solution. Greatest four digit number = 7621;

Smallest four digit number = 1267.

e. 5, 4, 0,3

Solution. Greatest four digit number = 5430;

Smallest four digit number = 3045.

Question 4. Now make the greatest and smallest 4-digit numbers by using any one digit twice. (Hint: Think in each case which digit will you use twice.)

a. 3,8,7

Solution. Greatest four digit number=8873;

Smallest four digit number = 3378.

b. 9,0,5

Solution. Greatest four digit number = 9950;

Smallest four digit number = 5009.

c. 0,4,9

Solution. Greatest four digit number = 9940;

Smallest four digit number = 4009.

d. 8,5,1

Solution. Greatest four digit number = 8851;

Smallest four digit number = 1158.

Rounding Off Numbers Class 6 Haryana Board

Question 5. Take two digits, say 2 and 3. Make 4-digit numbers using both the digits equal number of times.

Which is the greatest number?

Which is the smallest number?

How many different numbers can you make in all ?

Solution. Four digit numbers formed by using two digits 2 and 3 equal number of times are given below:

2233, 2323, 2332, 3223, 3232, 3322

The largest number is 3322

The smallest number is 2233

We can make in all 6 different numbers.

Question 6. Think of five more situations where you compare three or more quantities.

1. Comparing your marks to others
2. Comparing weight of two wrestlers
3. Comparing your height to other’s
4. Comparing the distance and the displacement.,
5. Comparing prices in the shop and on amazon.

Question 7. Arrange the following numbers in ascending order:

a. 847, 9754, 8320, 571

Solution. 571, 847, 8320, 9754

b. 9801, 25751, 36501, 38802

Solution. 9801, 25751, 36501, 38802

Question 8. Arrange the following numbers in descending order:

a. 5000, 7500, 85400, 7861

Solution. 85400, 7861, 7500, 5000

b. 1971, 45321, 88715, 92547

Solution. 92547, 88715, 45321, 1971

Question 9. Make ten such examples of ascending / descending order and solve them.

Question 1. 331, 198, 4403, 1311

Solution. Ascending Order: 198, 331, 1311, 4403

Descending Order: 4403, 1311, 331, 198

Question 2. 4314, 85222, 13, 4000

Solution. Ascending Order: 13, 4000, 4314, 85222

Descending Order: 85222, 4314, 4000, 13

Question 3. 144, 8520, 3381, 4018

Solution. Ascending Order: 144, 3381, 4018, 8520

Descending Order: 8520, 4018, 3381, 144

Roman Numerals Class 6 HBSE Maths

Question 4. 33, 980, 11384, 99

Solution. Ascending Order: 33, 99, 980, 11384

Descending Order: 11384, 980, 99, 33

Question 5. 304, 1405, 331, 84

Solution. Ascending Order :84, 304, 331, 1405

Descending Order : 1405, 331, 304, 84

Question 6. 247, 1578, 76, 14215

Solution. Ascending Order: 76, 247, 1578, 14215

Descending Order : 14215, 1578, 247, 76

Question 7. 1321, 618, 53, 12125

Solution. Ascending Order: 53, 618, 1321, 12125

Descending Order: 12125, 1321, 618, 53

Question 8. 7328, 14206, 48, 665

Solution. Ascending Order: 48, 665, 7328, 14206

Descending Order: 14206, 7328, 665, 48

Question 9. 536, 88, 11215, 7325

Solution. Ascending Order : 88, 536, 7325, 11215

Descending Order : 11215, 7325, 536, 88

Question 10. 228, 36, 10116, 3426

Solution. Ascending Order :36, 228, 3426, 10116

Descending Order: 10116, 3426, 228, 36

Question 10. Read and expand the numbers wherever there are blanks.

Write five more 5-digit numbers, read them and expand them.

Solution.

Question 11. Read and expand the numbers wherever there are blanks.

Solution.

Question 12. What is 10 – 1 = ?

Solution. 10 – 1 = 9

Question 13. What is 100 – 1 = ?

Solution. 100 – 199

Question 14. What is 10,000 – 1 = ?

Solution. 10,000 – 19,999

Question 15. What is 1,00,000 – 1 = ?

Solution. 1,00,000 – 199,999

Question 16. What is 1,00,00,000 – 1 = ?

Solution. 1,00,00,000 – 1 = 99,99,999

Question 17. Give five examples where the number of things counted would be more than 6-digit number.

Solution.

1. Number of people in our contry.
2. Number of copies of Ramayana published each year.
3. Number of grains in a sack full of wheat.
4. Number of railway tickets sold in a day at Railway Stations in Capital of India.
5. Number of saving account holders in Nationalised bank in a region.

Question 18. Starting from the greatest 6-digit number, write the previous five numbers in descending order.

Solution. The largest 6-digit number is 9,99,999. The next 5 numbers are:

10,00,000, 10,00,001, 10,00,002, 10,00,003, 10,00,004

In descending order, the next 5 numbers are:

10,00,004, 10,00,003 10,00,002, 10,00,001, 10,00,000

Question 19. Starting from the smallest 8-digit number, write the next five numbers in ascending order and read them.

Solution. The smallest 8-digit number is 1,00,00,000. The next 5 numbers in ascending order are:

1,00,00,001 one crore and one

1,00,00,002 one crore and two

1,00,00,003 one crore and three

1,00,00,004 one crore and four

1,00,00,005 one crore and five

Question 20. Read these numbers. Write them using placement boxes and then write expanded forms.

1)475320

2) 9847215

3) 97645310

4) 30458094

a) Which is the smallest number?

b) Which is the greatest number?

c) Arrange these numbers in ascending and descending orders?

Solution.

a) The smallest number is 475320

b) The greatest number is 97645310

c) The numbers in ascending order as follows 475320, 9847215, 30458094, 97645310.

The numbers in descending order are as follows: 97645310, 30458094, 9847215, 475320

Question 21. Read these numbers.

1) 527864

2) 95432

3) 18950049

4) 70002509

a) Write these numbers using placement boxes and then using commas in Indian as well as International system of numeration.

b) Arrange these in ascending and descending order.

Solution. a) 1. Using placement boxes:

2. Using commas:

Number             Number using commas

1) 527864             5,27,864
2) 95432               95,432
3) 18950049         1,89,50,049
4) 70002509         7,00,02,509

b) In ascending order, the numbers are 95432, 527864, 18950049, 70002509.

In descending order, the numbers are 18950049, 70002509, 527864, 95432.

Question 22. You have the following digits 4, 5, 6, 0, 7 and 8. Using them, make five numbers each with 6-digits.

a) Put commas for easy reading.

b) Arrange them in ascending and descending order.

Solution. The 5 numbers each with 6 digits using the digits 4, 5, 6, 0, 7 and 8 may be as given below.

876540

867540

876450

876045

867405

a) The above numbers putting commas are as given below.

8,76,540

8,67,540

8,76,450

8,76,045

8,67,405

b) The above numbers arranged in ascending order are as follows:

8,67,405

8,67,540

8,76,045

8,76,450

8,76,540

The above numbers arranged in descending order are as follows:

8,76,540

8,76,450

8,76,045

8,67,540

8,67,405

Question 23. Take the digits 4, 5, 6, 7, 8 and 9. Make any three numbers each with 8 digits. Put commas for easy reading.

Solution. The required numbers may be taken as given below.

9,88,77,456, 9,88,77,465, 9,88,77,654

Question 24. From the digits 3, 0 and 4 make five numbers each with 6 digits. Use commas.

Solution. The required numbers may be taken as given below.

3,00,343, 4,03,403, 4,44,330, 3,43,340, 4,40,340

Chapter 1 Knowing Our Numbers Exercise 1.1

Question 1. Fill in the blanks:

a) 1 lakh = …………………. ten thousand.

b) 1 million = ………………… hundred thousand.

c) 1 crore = …… ten lakh.

d) 1 crore = ……………….. million.

e) 1 million = ……………lakh.

Solution. a) 1 lakh = 10 ten thousand.

b) 1 million = 10 hundred thousand.

c) 1 crore = 10 ten lakh.

d) 1 crore = 10 million.

e) 1 million = 10 lakh.

Question 2. Place commas correctly and write the numerals:

a) Seventy three lakh seventy five thousand three hundred seven.

Solution. 73,75,307.

b) Nine crore five lakh forty one.

Solution. 9,05,00,041.

c) Seven crore fifty two lakh twenty one thousand three hundred two.

Solution. 7,52,21,302.

d) Fifty eight million four hundred twenty three thousand two hundred two.

Solution. 58,423,202.

e) Twenty three lakh thirty thousand ten.

Solution. 23,30,010.

Question 3. Insert commas suitably and write the names accroding to Indian System of Numeration:

a) 87595762

b) 8546283

c) 99900046

d) 98432701

Solution. a) 8,75,95,762 = Eight crores, seventy five lakhs, ninety five thousand, seven hundred and sixty two.

b) 85,46,283 = Eighty five lakhs, forty six thousand, two hundred and eighty three.

c) 9,99,00,046 = Nine crores, ninety-nine lakhs and forty six.

d) 9, 84, 32,701 = Nine crores, eighty four lakhs, thirty two thousand, seven hundred and one.

Question 4. Insert commas suitable and write the names accroding to international system of numeration:

a) 78921092

b) 7452283

c) 99985102

d) 48049831

Solution. a) 78,921,092 = Seventy eight million, nine hundred twenty one thousand ninety two

b) 7,452,283 = Seven million, four hundred fifty two thousand, two hundred eighty three.

c) 99,985,102 = Ninety nine million, nine hundred eighty five thousand, one hundred two.

d) 48,049,831 = Forty eight million, forty nine thousand, eight hundred thirty one.

Question 5. How many centimetres make a kilometre?

Solution. 1,00,000 centimeters = 1 kilometere.

Question 6. How many milligrams make one kilogram?

Solution. 10,00,000 milligrams = 1 kilogram.

Question 7. A box contains 2,00,000 medicine tablets each weighing 20 mg. What is the total weight of all the tablets in the box in grams and in kilograms?

Solution. Total weight of all the tablets in the box

= 2,00,000 x 20 mg. = 40,00,000 mg

= 4000 g [1g = 1000 mg]

= 4 kg

Question 8. A bus started its journey and reached different places with a speed of 60 km/hr. The journey is shown below.

1) Find the total distance covered by the bus from A to D.

2) Find the total distance covered by the bus from D to G.

3) Find the total distance covered by the bus, if it starts from A and returns back to A.

4) Can you find the difference of distances from C to D and D to E?

5) Find out the time taken by the bus to reach

a) A to B

b) C to D

c) E to G

d) Total journey

Solution. 1) Total distance covered by the bus from A to D

= 4170 km + 3410 km + 2160 km

= 9740 km.

2) Total distance covered by the bus from D to G.

= 8140 km + 4830 km + 2550 km

= 15520 km

3) Total distance covered by the bus

= Distance from A to D + Distance from D to G + Distance from G to A

= 9740 km + 15520 km + 1290 km = 26550 km

4) Distance from C to D = 2160 km

Distance from D to E = 8140 km

∴ Difference of distances from C to D and D to E = 8140 km – 2160 km = 5980 km.

5) a) Time taken by the bus to reach A to B.

= \(\frac{4170}{60} \text { hrs. }=\frac{417}{6} \text { hrs }=69 \frac{3}{6} \text { hrs. }\)

= 69 hrs 30 minutes

b) Time taken by the bus to reach C to D

= \(\frac{2160}{60} \mathrm{hrs}=36 \mathrm{hrs}\)

c) Time taken by the bus to reach E to G.

= \(\frac{4830+2550}{60} \mathrm{hrs}=\frac{7380}{60} \mathrm{hrs} .=123 \mathrm{hrs} .\)

d) Time taken by the bus for total journey

= \(\frac{26550}{60} \mathrm{hrs.}=442 \frac{1}{2} \mathrm{hrs.}\)

= 442 hrs. 30 minutes.

Question 9. Raman’s shop

The sales during the last year

a) Can you find the total weight of apples and oranges Raman sold last year?

Weight of apples: ………. kg

Weight of oranges = ……… kg

Therefore, total weight = ……… kg + ……. kg = …….. kg

Answer – The total weight of oranges and apples = ……. kg.

Solution. Weight of apples sold during the last year = 2457 kg.

Weight of oranges sold during the last year = 3004 kg.

Total weight of apples and oranges Raman sold during the last year.

= 2457 kg + 3004 kg

= 5461 kg.

Use Of Brackets And BODMAS Rule Class 6 HBSE

b) Can you find the total money Raman got by selling apples?

Solution. Total money Raman got by selling apples

= Rs. 2457 x 40

= Rs. 98,280

c) Can you find the total money Raman got by selling apples and oranges together?

Solution. Total money Raman got by selling Oranges

= Rs. 3004 × 30

= Rs. 90,120

∴ Total money Raman got by selling apples and oranges together. = 98,280 + 90, 120 = Rs. 1,88,400

d) Make a table showing how much money Raman received from selling each item. Arrange the entries of amount of money received in descending order. Find the item which brought him the highest amount. How much is this amount?

Solution.

The entries of amount of money received in descending order are as follows. Rs. 2,53,670, Rs. 2,40,012, Rs. 1,60,040, Rs. 98,280, Rs. 90,120, Rs. 68,280, Rs. 38,350 The items which bought him the highest amount is tooth brushes. This highest amount is Rs. 2,53,670.

Chapter 1 Knowing Our Numbers Exercise 1.2

Question 1. A book exhibition was held for four days in a school. The number of tickets sold at the counter on the first, second, third and final day was respectively 1094, 1812, 2050 and 2751. Find the total number of tickets sold on all the four days.

Solution. Number of tickets sold on the first day = 1094

Number of tickets sold on the second day = 1812

Number of tickets sold on the third day = 2050

Number of tickets sold on the final day = 2751

∴ Total number of tickets sold on all the four days 1094 + 1812 + 2050 + 2751 = 7707

Question 2. Shekhar is a famous cricket player. He has so far scored 6980 runs in test matches. He wishes to complete 10,000 runs. How many more runs does he need?

Solution. Runs scored so far = 6,980

Runs wished to be scored = 10,000

∴ Runs needed more = 10,000 – 6,980 = 3,020

Question 3. In an election, the successful candidate registered 5,77,500 votes and his nearest rival secured 3,48,700 votes. By what margin did the successful candidate win the election?

Solution. Votes registered by the successful candidate = 5,77,500

Votes secured by the nearest rival = 3,48,700

Margin by which the successful candidate won the election = 5,77,500 – 3,48,700 = 2,28,800

Question 4. Kirti bookstore sold books worth Rs. 2,85,891 in the first week of June, books worth Rs. 4,00,768 in the second week of the month. How much was the sale for the two weeks together? In which week was the sale greater and by how much?

Solution. Sale of the books in the first week = Rs. 2,85,891

Sale of books in the second week = Rs. 4,00,768

The sale was greater in the second week by

= Rs. 4,00,768 – Rs. 2,85,891

= Rs. 1,14,877

Question 5. Find the difference between the greatest and the least 5-digit number that can be written using the digits 6, 2, 7, 4, 3 each only once.

Solution. Greatest number that can be written using the digits 6, 2, 7, 4, 3 each only once = 76,432.

Least number that can be written using the digits 6, 2, 7, 4, 3 each only once = 23,467.

∴ Difference between the greatest and least numbers that can be written using the digits 6, 2, 7, 4, 3 each only once = 76,432 – 23,467 = 52,965

Question 6. A machine, on an average, manufactures 2,825 screws a day. How many screws did it produce in the month of January 2006 ?

Solution. Number of screws manufactured by the machine a day on an average = 2,825

Number of days in the month of January, 2006 = 31

∴ Number of screws produced by the machine in the month of January, 2006

= 2,825 x 3187,575.

Question 7. A merchant had Rs. 78,592 with her. She placed an order for purchasing 40 radio sets at Rs. 1200 each. How much money will remain with her after the purchase?

Solution. Money which the merchant had = Rs. 78,592

Cost of 40 radio sets = Rs. 1200 x 40 = Rs. 48,000.

∴ Money that will remain with the merchant after the purchase.

= Rs. 78,592 – Rs. 48,000

= Rs. 30,592.

Question 8. A student multiplied 7236 by 65 instead of multiplying by 56. By how much was his answer greater than the correct answer?

(Hint: Do you need to do both the multiplications?)

Solution. Wrong answer = 7236 x 65 = 4,70,340

Correct answer = 7236 × 56 = 4,05,216

∴ Wrong answer was greater than the correct answer by = 4,70,340, – 4,05,216

= 65,124

Question 9. To stitch a shirt, 2 m 15 cm cloth is needed. Out of 40 m cloth, how many shirts can be stitched and how much cloth will remain ?

(Hint: Convert data in cm.)

Solution. 2 m 15 cm = 2 x 100 cm + 15 cm

= 200 cm + 15 cm = 215 cm

40 m = 40 x 100 cm

= 4000 cm

No. of shirts that can be stitched = \(\frac{4000}{215}\) = 18 (approx)

∴ 18 shirts can be stitched and 130 cm cloth will remain.

Question 10. Medicine is packed in boxes, each weighing 4 kg 500 g. How many such boxes can be loaded in a van which cannot carry beyond 800 kg ?

Solution. 4 kg 500 g = 4 × 1000 g + 500 g

= 4000g + 500g = 4500 g.

800 kg = 800 x 1000 g = 800000 g.

Number of boxes loaded = \(\frac{800000}{4500}\) = 178

∴ 178 such boxes can be loaded. (Approximately)

Question 11. The distance between the school and the house of a student’s house is 1 km 875 m. Everyday she walks both ways. Find the total distance covered by her in six days.

Solution. 1 km 875 m = 1 x 1000 m +875 m

= 1000 m + 875 m

= 1875 m

Distance covered by her in a day in walking both ways between school and home.

= 1875 x 2 m

= 3750 m

∴ Total distance covered by her in six days. = 3750 x 6m

3 km 750 m × 6

= 22 km 500 m

∴ Distance covered in 6 days = 22 km 500 m.

Question 12. A vessel has 4 litres and 500 ml of curd. In how many glasses, each of 25 ml capacity, can it be filled?

Solution. 4 litres and 500 ml = 4500 ml. (∴ 1 litre = 1000 ml.)

Capacity of each glass = 25 ml

No. of glasses it can fill = \(\frac{4500}{25}\) = 180

∴ It can be distributed in 180 glasses.

Chapter 1 Knowing Our Numbers Very Short Answer Questions

Question 1. Write the numbers in ascending (increasing) order:

1) 375, 1475, 15951, 4713

Solution. 375, 1,475, 15,951, 4,713

Comparing the digits in thousands place 1, 15, 4

15 is the greatest; 1 is the smallest

Increasing order is 1, 4, 15.

∴ Ascending order: 375, 1475, 4713, 15951

2) 9,347; 19,035; 22,570; 12,300

Solution. 9,347; 19,035; 22,570; 12,300

Comparing the digits in thousands place 9, 19, 22, 12.

Increasing order of these digits – 9, 12, 19, 22.

∴ Ascending order: 9347, 12300, 19035, 22570.

Question 2. Write the numbers in descending (decreasing) order:

1) 1876, 89715, 45321, 89254

Solution. 1,876; 89,715; 45,321; 89,254

Comparing the digits in thousands place 1, 89, 45, 89.

Descending order: 89, 89, 45, 1

In 89,715 and 89,254 the thousands place 89 is same.

Now compare the digit in hundreds place.

Hundreds place digits are 7, 2.

2 is the smallest and 7 is the greatest.

∴ Descending order: 89,715; 89,254; 45,321; 1,876.

Difference Between Indian And International Number System

2) 3000, 8700, 3900, 18500.

Solution. 3,000; 8,700; 3,900; 18,500

Comparing the digits in thousands place 3, 8, 3, 18.

Descending order: 18,8,3,3 In 3000 and 3900, the thousands place 3 is same.

Now compare the digit in hundreds place.

Hundreds place digits are 0, 9. 0 is the smallest and 9 is the greatest.

Descending order: 18,500; 8,700; 3,900; 3,000.

Question 3. Write the numbers in words:

1) 72,642 = Seventy two thousand six hundred and forty two.

2) 55,345 = Fifty five thousand three hundred and forty five.

3) 66,600 = Sixty six thousand six hundred

4) 30,301 = Thirty thousand three hundred and one.

Question 4. Write the numbers in figures:

1) Forty thousand two hundred seventy – 40,270

2) Fourteen thousand sixty four – 14,064

3) Nine thousand seven hundred – 9,700

4) Sixty thousand – 60,000

Question 5. Write the numbers.

1) The smallest four digit number?

1,000

2) The greatest four digit number?

9,999

3) The smallest five digit number?

10,000

4) The greatest five digit number?

99.999

Question 6. Write the numbers in short form:

1) 3000 + 400 + 7 = 3407

2) 10000 + 2000 + 300 + 50 + 1 = 12351

3) 30000 + 500 + 20 + 5 = 30525

4) 90000 + 9000 + 900 + 90 + 9 = 99999

Question 7. Write the number in figures:

1) Four lakh fifty seven thousand four hundred.

2) Sixty lakh two thousand seven hundred seventy five.

3) Two crore fifty lakh forty thousand three hundred and three.

4) Sixty crore sixty lakh sixty thousand six hundred.

Solution. 1) 4,57,400

2) 60,02,775

3) 2,50,40,303

4) 60,60,60,600

Question 8. Write the expanded form of the number 315645.

Solution. 3,15,645 = 3 x 1,00,000 + 1 x 10,000 + 5 x 1,000 + 6 x 100 + 4 x 10 + 5 x 1

= 3,00,000 + 10,000 + 5,000 + 600 + 40 + 5

Question 9. Write the numbers 67456, 76547, 15476, 75460 in ascending and descending orders

Solution. Ascending order: 15476, 67456, 75460, 76547

Descending order: 76547, 75460, 67456, 15476

Question 10. Insert commas to separate periods and write the number 8555016916 in words in International system.

Solution. 8,555,016,916: Eight billion five hundred fifty five million sixteen thousand nine hundred and sixteen.

Question 11. Write the number 9030608878 in expanded form in International system.

Solution. Put commas for each period then the given number can be written as 9,030,608,878

9,030,608,878 = 9 x 1,000,000,000 + 3 x 10,000,000 + 6 × 100,000 + 0 x 10,000 + 8 x 1,000 + 8 x 100 + 7 × 10 + 8 × 1

Chapter 1 Knowing Our Numbers Short Answer Questions

Question 1. Write the expanded forms of the numbers:

1) 4348 = 4 x 1000 + 3 x 100 + 4 × 10 + 8 × 1

= 4000 + 300 + 40 + 8

2) 30214 = 3 x 10000+0x1000+2×100 + 1×10 +4×1

= 30000 + 200 + 10 + 4

3) 22222 = 2 × 10000 + 2 × 1000 + 2 x 100 + 2 × 10 + 2 × 1

= 20000 + 2000 + 200 + 20 + 2

4) 75025 = 7 x 10000 + 5 x 1000 + 0 x 100 + 2 x 10 + 5 x 1

= 70000 + 5000 + 20 + 5

Question 2. Write the smallest and greatest of all two digit, three digit, four digit, five digit, six digit, seven digit, eight digit numbers.

Solution.

Question 3. Write these numbers in words:

1) 12,36,99,140 – Twelve crores thirty six lakhs ninety nine thousand one hundred and forty.

2) 2,50,00,350 – Two crores fifty lakhs three hundred and fifty.

Question 4. Write the numbers using commas:

1) 11245670

2) 22402151

3) 30608712

4) 190308020

Solution. Using commas:

1) 1,12,45,670

2) 2,24,02,151

3) 3,06,08,712

4) 19,03,08,020

Question 5. Write the numbers in words:

1) 34,025

2) 7,09,115

3) 47,60,00,317

4) 6,18,07,000

Solution. 1) 34,025 = Thirty four thousand and twenty five.

2) 7,09,115 = Seven lakh nine thousand one hundred and fifteen.

3) 47,60,00,317 = Forty seven crore sixty lakh three hundred and seventeen.

4) 6,18,07,000 = Six crore eighteen lakh and seven thousand

Question 6. Write the numbers in expanded form:

1) 6,40,156

2) 63,20,500

3) 1,25,30,275

4) 75,80,19,202

Solution. 1) 6,40,156 = 6 × 1,00,000 + 4 x 10,000 + 0 x 1000 + 1 x 100 + 5 × 10 + 6 × 1

= 6,00,000 + 40,000 + 100 + 50 + 6

2) 63,20,500 = 6 x 10,00,000 + 3 x 1,00,000 + 2 x 10,000 + 0 x 1,000 + 5 × 100 + 0 × 10 + 0 × 1

= 60,00,000 + 3,00,000 + 20,000 + 500

3) 1,25,30,275 = 1 × 1,00,00,000 + 2 x 10,00,000 + 5 × 1,00,000 + 3 x 10,000 + 0 × 1,000 + 2 x 100 + 7 × 10 + 5 × 1

= 1,00,00,000 + 20,00,000 + 5,00,000 + 30,000 + 200 + 70 + 5

4) 75,80,19,202 = 7 × 10,00,00,000 + 5 x 1,00,00,000 + 8 x 10,00,000 + 0x 1,00,000 + 1 × 10,000 + 9 × 1,000 + 2 x 100 + 0 × 10 + 2 × 1.

= 70,00,00,000 + 5,00,00,000 + 80,00,000 + 10,000 + 9,000 + 200 + 2

Question 7. Write the following numbers in short form (Standard notation):

1) 50,00,000 + 4,00,000 + 20,000 + 8,000 + 500 + 20 + 4.

Solution. 54,28,524

2) 6,00,00,000 + 40,00,000 + 3,00,000 + 20,000 + 500 + 1.

Solution. 6, 43, 20, 501

3) 3,00,00,000 + 3,00,000 + 7,000 + 800 + 80 + 1.

Solution. 3, 03, 07, 881

4) 7,00,00,000 + 70,00,000 + 7,000 + 70

Solution. 7,70, 07, 070

Question 8. Write the greatest and smallest number formed by the digits 5, 3, 4, 0 and 7 and find their difference.

Solution. Greatest Number = 75430

Smallest Number = 03457

Difference = 71973

Note: In the problem they didn’t mention the difference between five digit numbers.

Question 9. Write the expanded form of the numbers:

1) 64

2) 325

3) 5078

4) 29500

Solution. 1) 64 = 6 × 10 + 4 × 1

= 60 + 4

2) 325 = 3 x 100 + 2 x 10 + 5 × 1

= 300 + 20 + 5

3) 5078 = 5 × 1000 + 0 x 100 + 7 x 10 + 8 x 1

= 5000 + 70 + 8

4) 29500 = 2 x 10,000 + 9 × 1,000 + 5 x 100 + 0 × 10 + 0 x 1

= 20,000 + 9,000 + 500

Question 10. How many millilitres will make a 1 kilolitre ?

Solution. 1 kilolitre = 1000 litres

= 1000 × 100 centilitres

= 1000 x 100 x 10 millilitres

1 kilolitre = 10,00,000 millilitres

Chapter 1 Knowing Our Numbers Long Answer Questions

Question 1. Write any ten numbers with digits 5 in crores, 2 in lakhs 1 in ten thousands, 6 in tens, 3 in ones place.

Solution. Ten numbers are

5,02, 10,063

5, 32, 16, 463

5, 42, 17,863

5,72, 19, 463

5,92, 12, 763

15, 82, 18, 563

25, 62, 13, 963

5, 22, 15, 663

5, 52, 14, 363

5, 12, 11, 263

Question 2. A box contains 1,00,000 Tablets (medicine) each weighing 20 mg. What is the weight of all the tablets in the box in both grams and kilograms?

Solution. Weight of each tablet = 20 mg

No. of tablets in the box = 1,00,000

∴ Weight of all the tablets in the box = 20 × 1,00,000

= 20,00,000 mg

1kg = 10,00,000 mg

20,00,000 mg = 2 x 10,00,000

= 2 x 1 kg = 2 kg

1 kg = 1000 gms

2 kg = 2 x 1000 = 2000 gms

Question 3. A petrol tanker contain 20,000 litres of petrol. Express the quantity of petrol in kilolitres and millilitres.

Solution. Quantity of petrol in the Tanker = 20,000 litres

1000 litres = 1 kilolitres

20,000 litres 20 x 1000 = 20 x 1 kilolitres

= 20 kilolitres

1 kilolitre = 10,00,000 millilitres

20 kilolitres = 20 × 10,00,000

= 2,00,00,000 millilitres

Class 6 HBSE Maths Chapter 1 Important Questions

Question 4. The cloth required to make a shirt of school uniform for each boy is 1 m 80 cm. How many shirts can tailor stitch using 40 m of cloth ? How much cloth will be left ?

Solution. Cloth required to make a shirt of school uniform for each boy = 1 m 80 cm

= 100 + 80 = 180 cm

Total length of the cloth = 40 m

= 40 x 100 4000 cm

No. of shirts stitched = \(\frac{4000}{180}\)

= 22

Length of the cloth left = 40 cm

Question 5. A hotel has 15 litres milk. 25 ml of milk is required to prepare a cup of tea. How many cups of tea can be made with the milk?

Solution. Quantity of milk in the hotel = 15 litres

= 15 × 1000

= 15000 ml

Milk required to prepare a cup of tea = 25 ml

Number of cups of tea that can be made with the milk = 15000 ÷ 25

= 600

Question 6. Write the following numbers in words in both Indian and International systems.

1) 6756327

Solution.

Indian system:

67,56,327 = Sixty seven lakhs fifty six thousand three hundred and twenty seven.

International system:

6,756, 327 = Six million seven hundred fifty six thousand three hundred and twenty seven.

2) 45607087

Solution.

Indian system:

4,56,07,087 = Four crore fifty six lakh seven thousand eighty seven.

International system:

45,607,087 = Forty five million six hundred seven thousand and eighty seven.

3) 8560707236

Solution.

Indian system:

856,07,07,236 = Eight hundred fifty six crore seven lakhs seven thousand two hundred and thirty six.

International system:

8,560,707,236 = Eight billion five hundred sixty million seven hundred seven thousand two hundred and thirty six.

Question 7. Write some daily life situations where we can use large numbers.

Solution.

1. To find out the distance between the Sun and the Earth.
2. To calculate the population of India.
3. The number of stars in the Universe.
4. The number of cells in the human body.
5. To find out the mass of earth.

Question 8. A box of medicine tablets contains 3,00,000 tablets each weighing 15mg. What is the total weight of all the tablets in the box in grams and in kilograms?

Solution. Number of tablets in the box = 3,00,000

Weight of each tablet = 15 mg

Total weight of the box = 3,00,000 x 15

= 45,00,000 mg

Total weight of the box in grams = \(\frac{4500000}{1000}\)

[∴ 1 gm = 1000 mg 1 mg = \(\frac{1}{1000}\) gr]

= 4500 grams.

The total weight of the box in kilograms = \(\frac{4500}{1000}\)

[∴ 1kg = 1000 gr 1 gr = \(\frac{1}{1000}\)kg]

= 4.5 kg

Question 9. Damodhar wants to buy onions in Kurnool market. Each onion bag’s weight is 45 kg. He loaded 326 onion bags with 45kg in a lorry. Find the total weight of onions in kilograms and quintals?

Solution. No. of onion bags that Damodhar loaded = 326 onion bags

The weight of each onion bag = 45 kg

The weight of 326 onion bags = 326 × 45

= 14670 kg

∴ The total weight of onions in kilograms = 14670 kg

∴ The total weight of onions in quintals = \(\frac{14670}{100}\)

[∴ 1 quintal = 100 kg 1 kg = \(\frac{1}{100}\)]

= 146.7 quintal

Chapter 1 Knowing Our Numbers Objective Type Questions

Choose the correct answer :

Question 1. The smallest five digit number

1. 1000
2. 9999
3. 10000
4. 99999

Answer. 3. 10000

Question 2. Place value of 2 in 632587

1. Lakhs
2. Tens
3. Hundreds
4. Thousands

Answer. 4. Thousands

Question 3. ‘Sixty lakhs six’ write in figures

1. 600006
2. 6000006
3. 660000
4. 60006

Answer. 2. 660000

Question 4. Round off 220 to their nearest hundred

1. 300
2. 200
3. 100
4. 400

Answer. 2. 200

Question 5. Number of digits in one crore

1. 7
2. 8
3. 9
4. 6

Answer. 2. 8

Question 6. 1 crore = ….. lakhs

1. 1000
2. 10
3. 100
4. \(\frac{1}{10}\)

Answer. 3. 100

Question 7. 1 lakh = ……. hundreds

1. 1000
2. 100
3. 10
4. 10000

Answer. 1. 1000

Question 8. 10 lakhs = ….. millions

1. 1
2. 10
3. 100
4. 1000

Answer. 1. 1

Question 9. 1 billion = ….. crores

1. 10
2. 100
3. 1000
4. 10000

Answer. 2. 100

Question 10. 302179468 the digit in the Ten millions place is

1. 1
2. 2
3. 0
4. 3

Answer. 3. 0

Question 11. 1 kg = …. gms

1. 10
2. 100
3. 10000
4. 1000

Answer. 4. 1000

Question 12. Quantity of oil in tankers, water in reservoirs are marked with

1. litres
2. millilitres
3. kilolitres
4. centilitres

Answer. 3. kilolitres

Question 13. How many thousands make a million?

1. 100
2. 1000
3. 10
4. 10000

Answer. 2. 1000

Question 14. Which of the 34895, 348891, 34899, 34893 number is smallest?

1. 34895
2. 34891
3. 34899
4. 34893

Answer. 2. 34891

Question 15. The number system which we use in our daily use

1. American
2. French
3. British
4. Hindu Arabic

Answer. 4. Hindu Arabic

Question 16. Number for “Seventy thousand six hundred and eight”

1. 70608
2. 706008
3. 70068
4. 70000608

Answer. 1. 70608

Question 17. Write 22021986 in international system using commas

1. 2,20,21,986
2. 220,21,986
3. 22,021,986
4. 2,202,1986

Answer. 3. 22,021,986

Question 18. Distance covered by a road roller in 1 turn it covers 400 mts. Distance covered by the road roller in 5 turns is

1. 80 mts
2. 200 mts
3. 2000 mts
4. 20000 mts

Answer. 3. 2000 mts

Question 19. 120 litres of milk will be supplied daily to a hotel. If each student is given 250 ml of milk then number of students are.

1. 48
2. 480
3. 24
4. 240

Answer. 2. 480

Question 20. Ascending order means

1. Smallest to greatest
2. Greatest to smallest
3. Both A & B
4. None

Answer. 1. Smallest to greatest

Question 21. Descending order means

1. Smallest to greatest
2. Greatest to smallest
3. Both A & B
4. None

Answer. 2. Greatest to smallest

Question 22. The numerical form of ‘sixty thousand sixty’ is

1. 60,066
2. 66,060
3. 60,060
4. 60606

Answer. 3. 60,060

Question 23. The greatest number formed by the digits 5,0,8,2

1. 5082
2. 8052
3. 8502
4. 8520

Answer. 4. 8520

Question 24. The smallest number formed by the digits 3, 7, 0,8

1. 3708
2. 3078
3. 3780
4. 8730

Answer. 2. 3078

Question 25. How many possible 4 digit numbers can be formed with digits 3, 0, 6, 4.

1. 24
2. 16
3. 18
4. 20

Answer. 3. 18

Question 26. How many possible 4 digit numbers can be formed with digits 2, 8, 3, 7.

1. 24
2. 18
3. 20
4. 26

Answer. 1. 24

Question 27. The greatest 5 digit number

1. 10000
2. 99989
3. 99999
4. 99990

Answer. 3. 99999

Question 28. The smallest 4 digit number

1. 1001
2. 9990
3. 9999
4. 1000

Answer. 4. 1000

Question 29. Who invented zero ?

1. Indians
2. Greeks
3. Romans
4. Italians

Answer. 1. Indians

Question 30. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 are called

1. Numbers
2. Place values
3. Digits
4. All the above

Answer. 3. Digits

Question 31. Ramanujan’s number

1. 1792
2. 1972
3. 1529
4. 1729

Answer. 4. 1729

Question 32. National Mathematics day

1. Jan 22
2. Dec 22
3. Feb 22
4. Aug 22

Answer. 2. Dec 22

Question 33. Which is the greatest among the following?

1. 67456
2. 76547
3. 15476
4. 75460

Answer. 2. 76547

Question 34. Which is the smallest among the following?

1. 64567
2. 66000
3. 60457
4. 64057

Answer. 3. 60457

Question 35. The ‘Predecessor’ of ‘1000’ is

1. 999
2. 1001
3. 990
4. 1010

Answer. 1. 999

Question 36. The ‘Successor’ of ‘989’ is

1. 988
2. 990
3. 980
4. 1000

Answer. 2. 990

Question 37. The place value of ‘4’ in the number 75460

1. 1000
2. 400
3. 100
4. 4

Answer. 2. 400

Question 38. The face value of ‘3’ in the number 27340

1. 100
2. 300
3. 30
4. 3

Answer. 4. 3

Question 39. How many 3 digit numbers are there in all ?

1. 999
2. 899
3. 900
4. 901

Answer. 3. 900

Question 40. How many thousands make one lakh ?

1. 10
2. 100
3. 1000
4. 10000

Answer. 2. 100

Question 41. 1 million =

1. 10 lakhs
2. 100 thousands
3. 1000 thousands
4. Both A & C

Answer. 4. Both A & C

Question 42. 1 Crore =

1. 1 million
2. 10 millions
3. 100 millions
4. None

Answer. 2. 10 millions

Question 43. 1 billion =

1. 10 crores
2. 100 crores
3. 1000 crores
4. 100 millions

Answer. 2. 100 crores

Question 44. How many millions make one billion?

1. 10
2. 100
3. 1000
4. 10,000

Answer. 3. 1000

Question 45. Which of the following is used to measure water flow?

1. Cusecs
2. T.M.C
3. Both A & B
4. None

Answer. 3. Both A & B

Question 46. 1 quintal =

1. 10 kg
2. 100 kg
3. 1000 kg
4. None

Answer. 2. 100 kg

Question 47. 1 tonne =

1. 10 kg
2. 100 kg
3. 1000 kg
4. 10000 kg

Answer. 3. 1000 kg

Question 48. The numerical form of ten crores ten thousand and ten

1. 10,00,00,010
2. 10,00,10,000
3. 10,00,10,010
4. 10,10,00,010

Answer. 3. 10,00,10,010

Question 49. The difference between the greatest and smallest numbers with the digits 3,0,7

1. 393
2. 403
3. 693
4. 423

Answer. 4. 423

Question 50. Find the sum of greatest and smallest numbers with the digits 3, 8, 0, 5.

1. 8,888
2. 11,588
3. 12,110
4. 11,591

Answer. 2. 11,588

Question 51. Find the difference between face values of ‘3’s of the number 53231 is

1. 0
2. 2,070
3. 3,030
4. 3,200

Answer. 1. 0

Question 52. Find the difference between place values of ‘8’s of the number 38283 is

1. 0
2. 7,920
3. 8,080
4. 79,920

Answer. 2. 7,920

Question 53. The sum of place values of 5’s of the number 2565 is

1. 495
2. 555
3. 505
4. 5005

Answer. 3. 505

Question 54. 1 litre =

1. 10 ml
2. 100 ml
3. 1000 ml
4. 10000 ml

Answer. 3. 1000 ml

Question 55. 1 meter3 =

1. 10 lt
2. 100 lt
3. 1000 lt
4. 10000 lt

Answer. 3. 1000 lt

Question 56. 1 metric ton =

1. 1 kg
2. 10 kg
3. 100 kg
4. 1000 kg

Answer. 4. 1000 kg

Question 57. 1 kilometer =

1. 100 mt
2. 1000 mt
3. 10000 mt
4. 10 mt

Answer. 2. 1000 ml

Question 58. The place value of ‘6’ of the number ‘536248’

1. 6000
2. 600
3. 60
4. 6

Answer. 1. 6000

Question 59. The face value of ‘3’ of the number 45329

1. 300
2. 100
3. 3
4. None

Answer. 3. 3

Question 60. The smallest number formed by the digits 3, 0, 6, 2

1. 2306
2. 2036
3. 2630
4. 6320

Answer. 2. 2036

Question 61. 1 crore =

1. 100 thousands
2. 1000 thousands
3. 1,00,000 thousands
4. 10,000 thousands

Answer. 4. 10,000 thousands

Fill In The Blanks

Fill in the blanks with suitable answer:

Question 62. Largest four digit number ……..

Answer. 9999

Question 63. The least four digit number with 1, 0, 2, 3 is ……

Answer. 1023

Question 64. The difference in the place values of 7 in 1,70,071 is ……..

Answer. 69,930

Question 65. …….. help us in reading and writing or large numbers easily.

Answer. commas

Question 66. 1 crore = …….. million

Answer. 10

Question 67. ……. is a good way of checking answers.

Answer. Estimation

Question 68. Smallest unit of weight is ……

Answer. milligrams

Question 69. Chandrika brought 4 kg 90 g apples, 2 kg 60 g grapes and 5 kg 300 g mangoes from a fruit shop. Total weight of the fruits is ……

Answer. 11 kg 450 g.

Question 70. Write the number 12,076,211 in words in international system ……..

Answer. Twelve millions seventy six thousand two hundred and eleven

Question 71. A train covers 120 km in 1 hour. How much distance it cover in 6 hours? …….

Answer. 720 km

Question 72. ……. are used for counting number of people in a village or a town.

Answer. large numbers

Question 73. In the International system of numeration commas are placed after every digits starting from the right.

Answer. 3

Question 74. The predecessor of 1001 is …..

Answer. 1000

Question 75. Numerical form of “Seventy Eight thousand four hundred and fourteen” is …….

Answer. 78,414

Question 76. 1 kg = ……. grams.

Answer. 1000

Question 77. The greater among the following number is ……

67456; 76547; 15476; 75460

Answer. 76547

Question 78. 100 crores = …….. billion.

Answer. 1

Question 79. Numerical form of “Ten crores ten thousand and ten” is …….

Answer. 10,00,10,010

Question 80. 67,56,326 when expressed in International system is …….

Answer. 6,756,326

Cubes

Question 1. If P = 999, then find the volume of P (p²+3p+3).

Solution:

Given P = 999

= P(P²+3843)

= 999 (1999)²+3 (999)+3)

= 999(99800142997+3)

= 999 (1001001)

= 999,999,999

The volume of P (p²+3p+3) = 999,999,999

Question 2. Find the Cube of:

1. 1001

Solution:

Given: 1001

= (1001)³

– (1001)²(1001)

= 1002001 (1001)

= 1,003,003,001

(1001)³ = 1,003,003,001

2. 998

Solution:

Given: 998

= (998)³

= (998)²(992)

= 996004 (998)

= 994,001,1992

(998)³ = 994,001,1992

Haryana Board Class 8 Maths Cubes and Cube Roots Solutions

3. 5a-4b

Solution:

Given 5a-4b

= (5a-4b)³ [∵ (a-b)² = a³-3ab+3ab²+b³]

= (5a)³ – 3(5a)²4b + 3(5a)(4b)²-(4b)³

= 125a³ – 300a²b + 240ab² – 64b³

(5a-4b)³  = 125a³ – 300a²b + 240ab² – 64b³

4. 3a-b+4c

Solution:

= 3a-b+4c

= (3a-b+4c)³ [(∵(a+b+c)³ = a³ + b³ + c² + 3 (a+b) (b+c) (c+a)]

= (3a)³ + (-b)³ + (4c)³ + 3(3a-b)(-b+4c) (4c+3a)

= 27a³ – b³ + 64c³ + 3((3a-b) (-4bc – 3ab + 16c² + 12ac)

= 27a³-b³ + 64c³ +3[-12abc – 9a²b + 48ac² + 36²c + 4b²c + 3ab² – 16bc² = 12abc]

= 27a³-b³ + 64c³ – 36abc – 27a²b + 144ac² + 108a²C +12b²c + 9ab² – 48bc² – 36abc

= 27a³ – b³ + 64c³ – 27a²b + 9a² + 108a²c – 72abc + 12b²c +144ac² – 48bc²

(3a-b+4c)³= 27a³ – b³ + 64c³ – 27a²b + 9a² + 108a²c – 72abc + 12b²c +144ac² – 48bc²

Class 8 Maths Chapter 7 Cubes Haryana Board

Question 3. Simplify:

1. 3.2 x 3.2 x 3.2 – 3 x 3.2 x 3-2 x 1.2 + 3 x 3.2 × 1.2 x 1.2 −1·2 x 1.2 x 1.2

Solution:

Given:

= 3.2 x 32 x 3.2 – 3 x 3.2 x 3.2 x 1.2 + 3 x 3.2 x 1.2 x 1.2-1.2 x 1.2 x 1.2

= (3.2)³-3 (3-2)² x 1-2 + 3 x 3.2 x (1.2)² -(1.2)³

= 32.768 – 36.864 + 13.824 – 1.728

= 8

3.2 x 32 x 3.2 – 3 x 3.2 x 3.2 x 1.2 + 3 x 3.2 x 1.2 x 1.2-1.2 x 1.2 x 1.2 = 8

2. (a-b+c)³ + (a+b-c)³ + 6a [a²-(b-c)²]

Solution

Given:

= (a-b+c)³ + (a+b-c)³ + 6a [a²-(b-c)²]

= a³ – b³ + c³ + 3(a-b)(-b+ c)(c+a) + a³ + b² – c³ + 3(a+b)(b-c)(-c+a) + 6a [a²– b² + c² + 2bc]

= a³ – b³ + c³ + 3(a-b)(-bc-ba+c²+ca) + a³ + b³ – c³ + 3(a+b)(-bc+ba+c²-ca) + 6a [a²-b²+c²+2bc]

= a³ – b³ + c³ + 3 (-abc – a²b + ac² + a²c + b²c + b²a – bc² – abc) + a³ + b³ – c³ + 3(-abc + a²b + ac² – a²c -b²c + b²a + bc² – abc)+ 6a³ – 6ab² + 6ac² + 12abc

= a³– b³ + c³ – 3abc – 3a²b + 3ac²+ 3a²c + 3b²C + 3b²a – 3bc² – 3abc + a³ + b³ – c³ – 3abc + 3a²b + 3ac² – 3a²c – 3b²c + 3b²a + 3bc² – 3abc + 6ab³ – 6ab² + 6ac² + 12abc

= a³ – 3abc + 3ac² + 3b²a – 3abc – 3abc + 3ac² + 3b²a – 3abc + 6a³ – 6ab² + 6ac² + 12abc

= 8a³ – 12abc + 6ac² + 6ab² – 6ab² – 6ac² + 12abc

= 8a³

(a-b+c)³ + (a+b-c)³ + 6a [a²-(b-c)²] = 8a³

Haryana Board 8th Class Maths Cube and Cube Root Questions and Answers

Question 4. If a-b = 8 then find the value of (a³-b³-24ab)

Solution:

Given: a-b=8

= a³-b³-24ab

= (a)³ – (b)³ -24ab

= (a-b)³ + 3 x a x b(a-b)- 24ab

= (8)³ +3ab (8)-24ab

= 512 + 24ab – 24ab

= 512

The value of (a³-b³-24ab) = 512

Question 5. Find the value of 8x³-36x²+54x-30 lf x=-5

Solution:

Given: X=-5

= 8x³-36x²+54x – 30

= 8(-5)³ – 36(-5)² + 54(-5)-30

= 8(-125)-36(25)-270-30

= -1000-900-270-30

= 1900+300

= 2200

The value of 8x³-36x²+54x-30 = 2200

Chapter 7 Cubes Class 8 Solutions in Hindi Haryana Board

Question 6. Find the product of the following:

1. (x-3)(x²+3x+9)

Solution:

Given: (x-3)(x²+3x+9)

= x³ + 3x² + 9x – 3x² – 9x – 27

= x³-27

(x-3)(x²+3x+9) = x³-27

2. (a²+b²)(a⁴-a²b²+b⁴)

Solution:

Given (a²+b²)(a⁴-a²b²+b⁴)

= (a²+b²)(a⁴-a²b²+b⁴)

= a²(a⁴-a²b²+b⁴) + b²(a⁴-a²b²+b⁴)

= a⁶ – a⁴b² + a²b⁴ + b²á⁴ – a²b⁴+ b⁶

= a⁶+b⁶

(a²+b²)(a⁴-a²b²+b⁴) = a⁶+b⁶

Haryana Board Class 8 Maths Exercise 7.1 Solutions

3. (4a²-9b²) (4a²+6ab+9b²) (4a²-6ab+9b²)

Solution:

Given: (4a²-9b²) (4a²+6ab+9b²) (4a²-6ab+9b²)

= (4a²(4a²+6ab+9b²)-9b²(4a²+6ab+9b²))(4a²-6ab+9b²)

= (16a⁴ + 24a³b + 36a²b² – 36a²b² – 54ab³ – 81(b⁴)(4a²-6ab+9b²)

= 64a⁶ + 96a⁵b – 216a³b³ – 324a²b⁴ – 96a⁵b – 144a⁴b² + 324a²b⁴ + 486ab⁵ + 144a⁴b² + 216a³b³ – 486ab⁵ – 729b⁶

= 64a⁶ – 729b⁶

(4a²-9b²) (4a²+6ab+9b²) (4a²-6ab+9b²) = 64a⁶ – 729b⁶

Question 7. Resolve into factors:

1. \(a^3-9 b^3-3 a b(a-b)\)

Solution:

Given: \(a^3-9 b^3-3 a b(a-b)\)

= \(a^3-9 b^3-3 a b(a-b)\)

= \(a^3-b^3-3 a b(a-b)-8 b^3\)

= \((a-b)^3-(2 b)^3\)

= \((a-b-2 b)\left\{(a-b)^2+(a-b) \cdot 2 b+(2 b)^2\right\}\)

= \((a-3 b)\left(a^2-2 a b+b^2+2 a b-2 b^2+4 b^2\right)\)

= \((a-3 b)\left(a^2+3 b^2\right)\)

\(a^3-9 b^3-3 a b(a-b)\) = \((a-3 b)\left(a^2+3 b^2\right)\)

Important Questions for Class 8 Maths Chapter 7 Haryana Board

2. a¹² – b¹²

Solution:

Given a¹² – b¹²

= (a⁶)² – (b⁶)²

= \(\left(a^6+b^6\right)\left(a^6-b^6\right)\)

= \(\left\{\left(a^2\right)^3+\left(b^2\right)^3\right\}\left\{\left(a^3\right)^2-\left(b^3\right)^2\right\}\)

= \(\left(a^2+b^2\right)\left\{\left(a^2\right)^2-a^2 b^2+\left(b^2\right)^2\right\}\left(a^3+b^3\right)\left(a^3-b^3\right)\)

= \(\left(a^2+b^2\right)\left(a^4-a^2 b^2+b^4\right)(a+b)\left(a^2-a b+b^2\right)(a-b)\left(a^2+a b+b^2\right)\)

= \((a+b)(a-b)\left(a^2+b^2\right)\left(a^2+a b+b^2\right)\left(a^2-a b+b^2\right)\left(a^4-a^2 b^2+b^4\right)\)

a¹² – b¹² = \((a+b)(a-b)\left(a^2+b^2\right)\left(a^2+a b+b^2\right)\left(a^2-a b+b^2\right)\left(a^4-a^2 b^2+b^4\right)\)

Question 8. Choose the Correct answer:

1. The Cube of 99 is

1. 972099
2. 970299
3. 979029
4. 972909

Solution:

=(99)³

= (99)² 99

= 9801 x 99

= 970299

(99)³ = 970299

The Correct answer is (2).

Step-by-Step Solutions for Cubes Class 8 Haryana Board

2. If a+b+c=0, then a³+b³+c³ = ?

1. 3abc
2. abc
3. c
4. none of these

Solution:

= a³ + b³ + c³

= (a+b)³ -3ab (a+b) + c³

= (-c)³-3ab (-c) +c³ [a+b+c=0)

= -c³+3abc+c³

= 3abc

a³ + b³ + c³ = 3abc

So the Correct answer is (1).

3. If a-b=1 and a³-b³=61, then the Value of ab is

1. 10
2. 20
3. 30
4. none of these

Solution:

= a³-b³=61

= (a-b)³ + 3ab (a-b) = 61

= (1)³ + 3ab(1) = 61

= 3ab = 61-1

= 3ab = 60

= ab = \(\frac{60}{3}\)

= ab = 20

So, the Correct answer is (2).

Question 9. write ‘True’ or ‘False”.

1. 216 is not a perfect Cube.

Solution:

216 = 36×6

216= 6x6x6

216=(6)³

The statement is False.

2. 1729 is a Hardy Ramanujam number.

Solution: The statement is true.

3. p³q³+1 = (pq-1)(p²q² + pq + 1)

Solution:

p³q³ + 1 = (pq)³ + (1)³

p³q³ + 1= (pq+1){(pq)² – pq.1 + (1)2}

p³q³ + 1= (pq+1) (p²q² – pq+1)

Statement is False.

Question 10. Fill in the blanks.

1. The Cube root of Single digit number may also be a _________ digit number.

Solution: Single.

2. a³+b³ = ___________ x (a²-ab+b²)

Solution: a³ + b³ = (a+b) (a²-ab+b²)

3. (a+b)³ = a² + b³ + __________.

Solution: (a+b)³ = a³ + b³ + 3ab(a+b)

Factorisation Of Algebraic Expressions

Question 1. Resolve into factors:

1. x² – 22x + 120

Solution:

Given: x² – 22x + 120

= x²-10x-12x-120

= x(x-10)-12(x-10)

= (x-10) (x-12)

x² – 22x + 120 = (x-10) (x-12)

2. 40+3x-x²

Solution:

Given: 40+3x-x²

= 40+8x-5x-x²

= 8(5+x)-x(5+x)

= (8-x)(5+x)

40+3x-x² = (8-x)(5+x)

Haryana Board Class 8 Maths Factorisation Solutions

3. (a²-a)²-8(a²-a)+12

Solution:

Given: (a²-a)²-8(a²-a)+12

= (a²-a)² – 6(a²-a)-2(a²-a)+12

= (a²−a)((a²-a)−6)-2((a²-a)-6)

= (a²-a-2) (a²-a-6)

= (a²+a-2a-2)(a²3a+2a-6)

= (a(a+1)-2(a+1))(a(a-3)+2(9-3))

= (a+1) (a-2) (a+2) (a-3)

(a²-a)²-8(a²-a)+12 = (a+1) (a-2) (a+2) (a-3)

4. x²-√3x-6

Solution:

Given: x²-√3x-6

= x²-2√3x+√3x-6

= x(x-2√3)+ √3(x-2√3)

= (x+√3)(x-2√3)

x²-√3x-6 = (x+√3)(x-2√3)

Class 8 Maths Chapter 14 Factorisation Haryana Board

5. (x+1)(x+3)(x-4)(x-6)+13

Solution:

Given (x+1)(x+3)(x-4)(x-6)+ 13

= (x²+3x+x+3)(x²-6x-4x+24)+13

= (x²+4x+3)(x²-10x+24)+13

= x⁴-10x³+24x²+4x³40x²+96x+3x² = 30x+72+13

= x⁴-6x³-13x²-66+85

= x⁴-3x³-3x³-17x²+9x²– 5x²+51x+15x+85

= x⁴-3x³-17x²-3x³+9x²+51x-5x²+15x+85

= x²(x²-3x-17)-3x(x²-3x-17)-5(x²-3x-17)

= (x²-3x-5)(x²-3x-17)

(x+1)(x+3)(x-4)(x-6)+ 13 = (x²-3x-5)(x²-3x-17)

6. 21x² + 40xy – 21y²

Solution:

Given: 21x²+40xy-21y²

= 21x² – 9xy + 49xy – 21y²

= 3x(7x-3y) + 7y(7x-3y)

= (3x+7y)(7x-3y)

21x²+40xy-21y² = (3x+7y)(7x-3y)

Haryana Board 8th Class Maths Factorisation Questions and Answers

7. 4(2a-3)² -3(2a-3) (a-1)-7(a-1)²

Solution:

Given: 4(2a-3)²-3(2a-3) (a-1)-7(a-1)²

= 4(4a²-(2a+9)-3(2a²-2a-3a+3)-7(a²+1-2a)

= 16a² – 48a + 36 – 6a² + 6a + 9a – 9 – 7a² – 7 + 14

= 3a² – 19a + 20

= 3a² – 15a – 4a +20

= 3(a-5)-4(a-5)

4(2a-3)²-3(2a-3) (a-1)-7(a-1)² = (3a-4) (a-5)

8. (a+7) (a-10) + 16

Solution:

Given: (a+7)(a-10)+16

= a²-10a+7a-70+16

= a²-3a-54

= a-9a+6a-54

= a(a-9)+6(a-9)

=(a+6)(a-9)

(a+7)(a-10)+16 =(a+6)(a-9)

Chapter 14 Factorisation Class 8 Solutions in Hindi Haryana Board

9. (a²+4a)²+21(a²+4a)+98

Solution:

Given: (a²+4a)²+21(a²+4a)+98

= a⁴ + 8a³ + 16a² + 2(a²+4a)+ 98

= a⁴ + 8a³ + 37a² +84a +98

= a⁴+4a³+14a²+4a³+16a²+56a+7a²+28+98

= a² (a²+4a+14)+4a(a²+4a+14) +7(a²+4a+14)

= (a²+4a+7) (a² + 4a + 14)

(a²+4a)²+21(a²+4a)+98 = (a²+4a+7) (a² + 4a + 14)

10. (2a²+ 5a) (2a² + 5a-19) +84

Solution:

Given: (2a²+ 5a) (2a² + 5a-19) +84

= 4a⁴ + 10a³ – 38a² + 10a³ + 25a² – 95a + 84

= 4a⁴ + 20a³ – 13a² – 95a + 84

= 4a⁴ + 8a³ – 21a² + 12a³ + 24a² – 63a -16a² – 32a + 84

= a²(4a²+8a-21)+3a(4a²+8a-21)-4(4a²+8a-21)

= (a²+3a-4) (4a² +8a-21)

= (a²+4a-a-4) (4a² + 14a-6a-21)

= ((a+4)a-1(a+4)) (2a(2a+7)-3(2a+7))

= (a-1) (a+4) (2a-3)(2a+7)

(2a²+ 5a) (2a² + 5a-19) +84 = (a-1) (a+4) (2a-3)(2a+7)

11. 8x⁴+2x²-45

Solution:

Given: 8x⁴+2x²-45

= 8x² + 20x² – 18x² – 45

= 4x² (2x²+5)-9(2x²+5)

= (2x²+5)(4x²-9)

= (2x+5) (4x²-6x+6x-9)

= (2x²+5) (2x(2x-3)+3(2x-3))

= (2x²+5)(2x+3)(2x-3)

8x⁴+2x²-45 = (2x²+5)(2x+3)(2x-3)

Haryana Board Class 8 Maths Exercise 14.1 Solutions

12. xv-x-(a-3)(a-2)

Solution:

Given: x²-x-(a-3)(a-2)

= x²-x-(a²-2a-3a+6)

= x²-x-a²+5a-6

= x²-3x+2x-a²+ax-ax+3a+2a-6

= x²+ax-3x-ax-a²+3a+2x+2a-6

= x(x+a-3)-a(x+a-3)+2(x+a-3)

=(x-a+2)(x+a-3)

x²-x-(a-3)(a-2) =(x-a+2)(x+a-3)

13. 99x²-20xy+99y²

Solution:

Given: 99x²-20xy+99y²

= 99x²-81xy-121xy+99y²

= 9x (11x-9y)-11y (11x-94)

= (9x-114) (11x-94)

99x²-20xy+99y²  = (9x-114) (11x-94)

Question 2. Resolve the following expressions into factors by expressing them as the diffence of two Squares:

1. x²-5x-6

Solution:

Given: x²-5x-6

= x²-6x+x-6

= x(x-6)+1(x-6)

= (x+1)(x-6)

x²-5x-6 = (x+1)(x-6)

2. 3+x-10x²

Solution:

Given: 3+x-10x²

= 3+6x-5x-10x²

= 3(1+2x)-5x(1+2x)

= (3-5x) (1+2x)

3+x-10x² = (3-5x) (1+2x)

3. 8x-3-4x²

Solution:

Given: 8x-3-4x²

= 6x+2x-3-4x²

= 6x-3+2x-4x²

= 3(2x-1)-2x(2x-1)

= (3-2x) (2x-1)

8x-3-4x²= (3-2x) (2x-1)

4. 6(a+b)²+5(a²-b²)-6 (a-b)²

Solution:

Given: 6(a+b)²+5(a²-b²)-6(a-b)²

= 6(a²+b²+2ab)+5a²-5b²-6(a²+b²-2ab)

= 6a²+6b²+ 12ab+ 5a²-5b²-6a²-6b² +12ab

= 5a²+24ab-5b²

= 5a² +25ab-ab-5b²

= 5a(a+5b)-b(a+5b)

= (5a-b)(a+5b)

6(a+b)²+5(a²-b²)-6(a-b)² = (5a-b)(a+5b)

5. 6x²-13x+6

Solution:

Given: 6x²-13x+6

= 6x²-9x-4x+6

= 3x(2x-3)-2(2x-3)

=(3x-2)(2x-3)

6x²-13x+6 =(3x-2)(2x-3)

Question 3. Choose the Correct answer:

1. x²-3x-28 = ?

1. (x+4)(x+7)
2. (x+4)(x-7)
3. (x-4)(x+7)
4. (x-4)(x-7)

Solution:

x²-3x-28

= x²-7x+4x-28

= x(x-7)+4(x-7)

= (x+4) (x-7)

x²-3x-28 = (x+4) (x-7)

The Correct answer is (2)

Important Questions for Class 8 Maths Chapter 14 Haryana Board

2) If (5x²-4x-9) = (x+1)(5x+P), then the value of P is

1. 9
2. 5
3. -9
4. none of these

Solution:

= 5x²-4x-9

= 5x²-9x+5x-9 = x(5x-9)+1(5x-9)

= (5x-9)(x+1)

= (x+1)(5x+P)= (x+1) (5x-9)

= 5x + P = 5x-9

⇒ P = -9

The value of P = -9

The Correct answer is (3).

3. 2a²+b²-c²+3ab+ac = ?

1. (a+b+c)(2a+b+c)
2. (a+b+c)(2a+b-c)
3. (a+b+c) (2a-b-c)
4. none of these

Solution:

2a²+b²-c²+3ab+ac

= 2a²+ab-ac+2ab+b²-bc+2ac + bc-c²

= a(2a+b-c)+b(2a+b-c) + C(2a+b-c)

= (a+b+c) (2a+b-c)

2a²+b²-c²+3ab+ac = (a+b+c) (2a+b-c)

The Correct answer is (2).

Question 4. write ‘True’ or ‘False’:

1. The Factors of (x²-xy-30y²) is (x+5y)(x-64).

Solution:

x²-xy-30y² = x²-6xy+5xy-30y²

= x(x-6y) +5y(x-6y) = (x-6y) (x+5y)

The statement is true.

Step-by-Step Solutions for Factorisation Class 8 Haryana Board

2. a³-b³-a(a²-b²)+b(a-b)²=ab(a-b)

Solution:

a³-b³-a(a²-b²)+b(a-b)²=ab(a-b)

= a³-b³-a³+ab²+b(a²+b²-2ab)

= -b³+ab²+ba²+b³-2ab²

= a²b-ab² = ab(a-b)

The statement is true.

3.(x-1)(x+9)+21=(x+6)(x-2)

Solution:

(x-1)(x+9)+21

= x²+9x-x-9+21

= x²+8x+12

= x²+6x+2x+12

= x(x+6)+2(x+6)

= (x+2)(x+6)

The statement is false.

Question 5. Fill in the blanks:

1. (x+a)(x+b) = x²+(a+b)x + _______.

Solution:

(x+9)(x+6) = x(x+b)+a(x+b)

= x²+bx+ax+ab = x²+(a+b)x+ab

2. (a+b+c)³ = a³ + b² + c² + __________.

Solution:

3(a+b)(b+c)(c+a).

• Chapter 1 Rational Numbers
• Chapter 2 Linear Equation in One Variable
• Chapter 3 Understanding Quadrilaterals
• Chapter 4 Practical Geometry
• Chapter 5 Data Handling
• Chapter 6 Square and Square Roots
• Chapter 7 Cube and Cube Roots
• Chapter 8 Comparing Quantities
• Chapter 9 Algebraic Expressions and Identities
• Chapter 10 Visualising Solid Shapes
• Chapter 11 Mensuration
• Chapter 12 Exponents and Powers
• Chapter 13 Direct and Indirect Proportions
• Chapter 14 Factorisation
• Chapter 15 Introduction to Graphs
• Chapter 16 Playing with Numbers